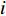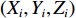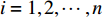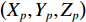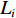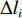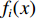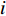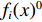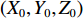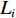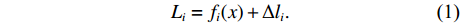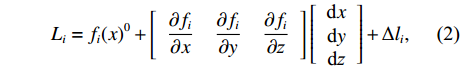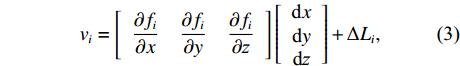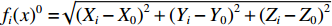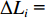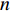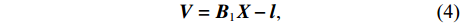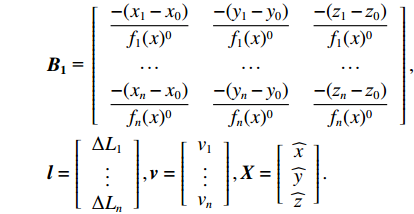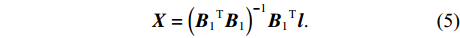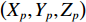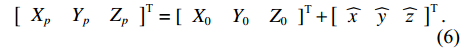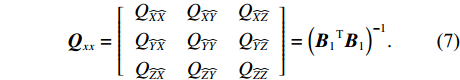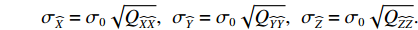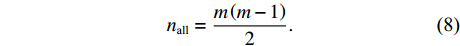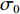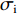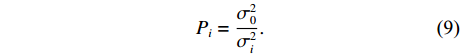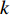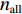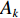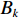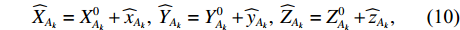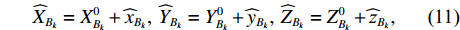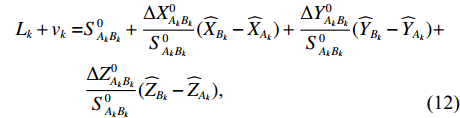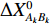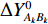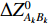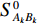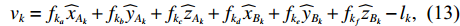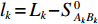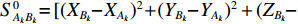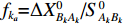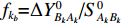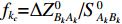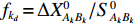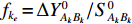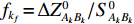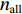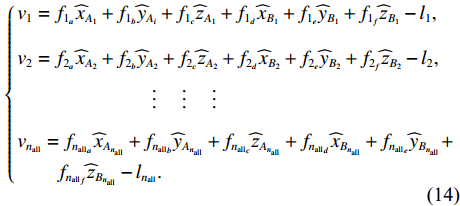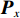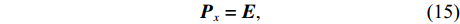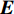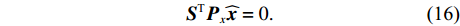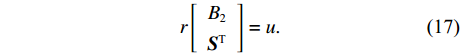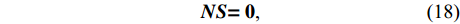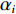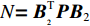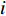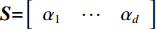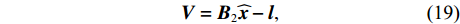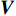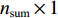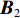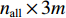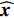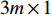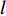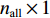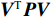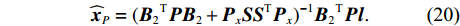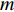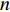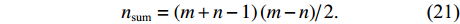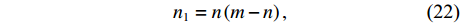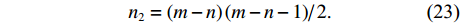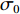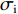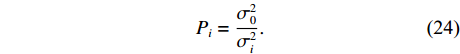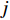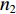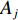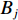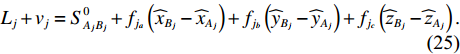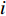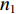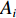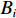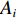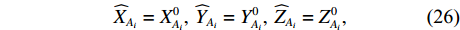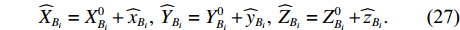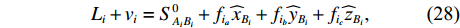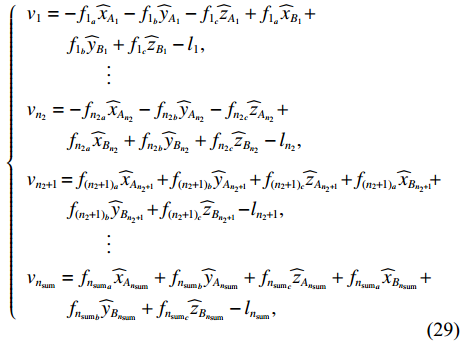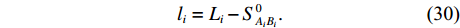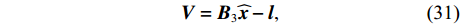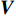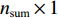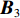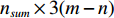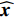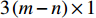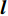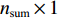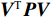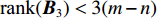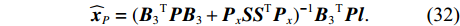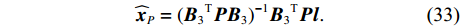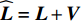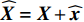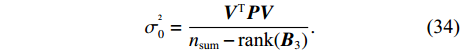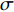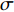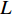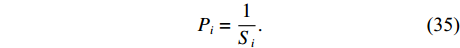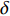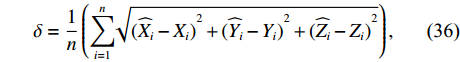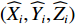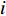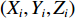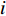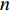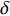Rapid calibration method for rank defect submarine geodetic station network
-
摘要:
基于信标互测距信息与绝对坐标信息的融合, 提出一种海洋大地控制网快速标校方法。相较于现有方法, 快速标校方法降低了自由网平差对起算条件的需求, 减少了50%以上的绝对标定点数目, 标校效率与绝对坐标精度显著提升。在大范围布设时, 优势明显。此外, 通过对阵型与绝对校准点数目的分析, 提出了几种典型阵型在理想条件下的布设方案。浅水试验结果表明, 在保证基准网标校精度高于0.2 m的条件下, 标校效率提升了50%。
Abstract:A rapid calibration method for marine geodetic control networks based on the combination of beacon mutual ranging information and absolute coordinate information is proposed. Compared with existing methods, the rapid calibration method reduces the initial condition restriction of free net adjustment; the number of absolute calibration points is reduced by more than 50%, and the calibration efficiency and absolute coordinate precision are significantly improved. In addition, several typical formations under ideal conditions are proposed by analyzing the formations and absolute calibration points. The shallow water test results show that the calibration efficiency is improved by 50% when the calibration precision of the reference network is greater than 0.2 m and the calibration precision of the reference network is greater than 0.2 m.
-
引言
海底大地基准网是一组布放在海底的大地测量基准站, 它类似于GNSS星座, 既可对水面及水下用户提供定位、导航和授时服务, 也可用于监测海底板块运动和海洋环境变化。与卫星定位为主要技术手段的陆地及海面定位不同, 电磁波传播拒止条件下, 以声波为信息载体的水声定位技术是海底大地基准的精密获取的主要选择。
许多发达国家已经具备基准网布设与维护的能力[1-3]。比如日本用于监测地质活动所布设的海洋大地基准网 [4-5]。2015年, 美国国防高级研究计划局(DARPA)提出的构建“深海GNSS”以协助潜器获取高精度的定位信息。
传统海底大地基准标定通过综合试验船基阵大地坐标、基阵与海底基准点的相对坐标实现海底基准点的绝对标定[6]。然而基准点标定十分困难, 不仅标定时间长, 且受声速影响严重[7-9]。文献[7]通过集成测量方位和测距的方法实现对基准点位置的标定, 标定时间相比于传统的18~24 h已经缩短至2~3 h。但在实现大范围的长基线定位时, 如美国Proserv公司NASNet长基线系统海洋石油工程管道站点布设等海洋工程作业时, 其控制点布设最多时可达77个。因此, 从总体上减少绝对标定点数目, 提高布设效率是十分有必要的。
文献[8]通过增加基准的功能来实现基线间的自动测量和校准。文献[9]分析了相对测阵的原理, 给出了相对测阵和绝对测阵的坐标转换。文献[10]考虑了基准网的阵型设计与优化。但以上研究均未能有效提升整体标校效率。
文献[11]通过对控制网内基准点分别进行绝对标定, 得到每一个基准点的精确初始位置。然后通过基准点之间的相对测量信息, 在深度或者其他观测信息的约束下, 对网内全部基准点进行坐标的修正, 其本质是秩亏自由网平差, 虽然基准的内符合精度会相应提升, 但是会损失一部分的外符合精度, 且在大面积布网时, 作业效率低下。
文献[12]利用深度约束, 将三维控制网的起算条件从3个控制点下降至2个点。文献[13-14]在文献[12]的基础上, 利用三维无约束平差剔除不合格基线, 从而提高网平差精度。虽然提升了绝对标校效率, 但需要额外获取信标深度信息。
为解决上述问题, 本文提出了一种海底大地基准快速标校方法。该方法降低了需要绝对标定的基准点数目, 无需额外观测信息补偿, 从根本上实现校准效率的提升。此外将绝对标定结果引入误差方程, 在不降低控制网相对坐标精度的前提下, 提高了网平差后的绝对精度。
1. 海底大地基准快速标校方法原理
海底大地基准快速标校法, 是利用海面母船圆走航完成部分海洋大地控制点标定。在此基础上, 不同控制点之间互测距组成测边网, 采用网平差处理得到海洋大地控制网每个控制点的坐标, 完成海洋大地控制网的快速校准, 最终实现陆海面基准到海底的传递[15-18]。
1.1 海面圆走航绝对标定
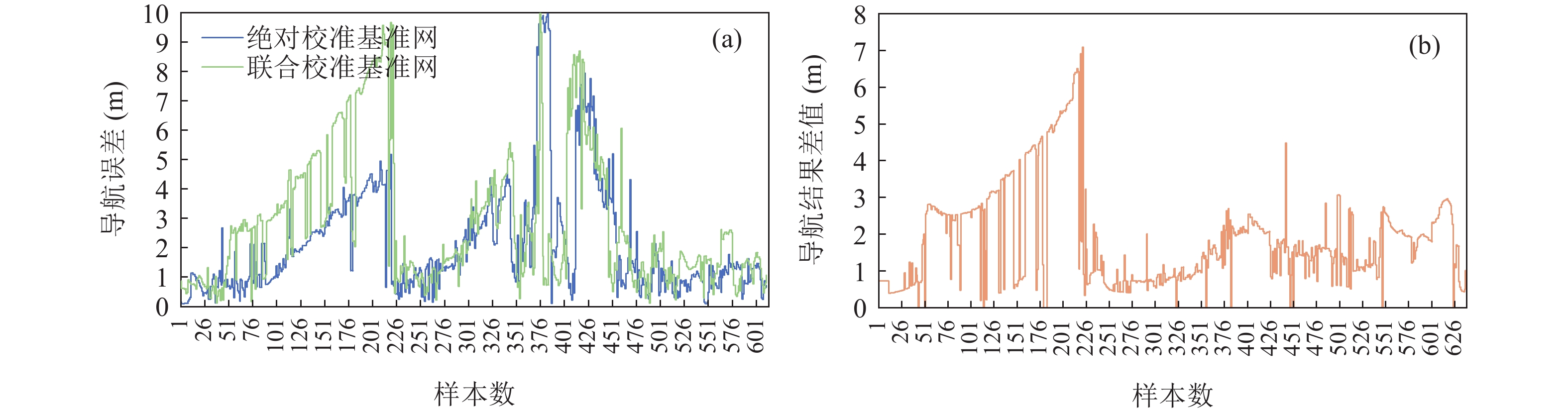
海面圆走航是基于距离交汇的绝对标定方法, 轨迹的对称性可以消除该方法的部分系统误差。基于该思想, 文献[6]提出了工作母船圆走航观测, 通过获取对称距离实现单个阵元的绝对标定, 同时完成测量基准向海底的传递。其走航方式如图1所示。
设第
i 次观测时船载基阵的地理坐标为(Xi,Yi,Zi) ,i=1,2,⋯,n 。待测定的海底基阵阵元的坐标为(Xp,Yp,Zp) , 利用声线跟踪得到两者之间的斜距离观测量为Li [19], 测量误差为Δli 。fi(x) 为第i 次观测时船载基阵至阵元之间的距离函数,fi(x)0 为方程在基阵初值(X0,Y0,Z0) 处的值,Li 可表达为Li=fi(x)+Δli. (1) 对上式线性化得:
Li=fi(x)0+[∂fi∂x∂fi∂y∂fi∂z][dxdydz]+Δli, (2) 则误差方程为
vi=[∂fi∂x∂fi∂y∂fi∂z][dxdydz]+ΔLi, (3) 其中,
fi(x)0=√(Xi−X0)2+(Yi−Y0)2+(Zi−Z0)2 ,ΔLi = fi(x)0−Li .由
n 条测量距离构建如下矩阵形式:{\boldsymbol{V}} = {{\boldsymbol{B}}_1}{\boldsymbol{X}} - {\boldsymbol{l}}, (4) 其中
\begin{split}& {{\boldsymbol{B}}_{\boldsymbol{1}}}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {\dfrac{{ - ({x_1} - {x_0})}}{{{f_1}(x)_{}^0}}}&{\dfrac{{ - ({y_1} - {y_0})}}{{{f_1}(x)_{}^0}}}&{\dfrac{{ - ({{\textit{z}}_1} - {{\textit{z}}_0})}}{{{f_1}(x)_{}^0}}} \\ \cdots & \cdots & \cdots \\ {\dfrac{{ - ({x_n} - {x_0})}}{{{f_n}(x)_{}^0}}}&{\dfrac{{ - ({y_n} - {y_0})}}{{{f_n}(x)_{}^0}}}&{\dfrac{{ - ({{\textit{z}}_n} - {{\textit{z}}_0})}}{{{f_n}(x)_{}^0}}} \end{array}} \right],\\&{\boldsymbol{l}} = \left[ {\begin{array}{*{20}{c}} {\Delta {L_1}} \\ \vdots \\ {\Delta {L_n}} \end{array}} \right],{\boldsymbol{v}} = \left[ {\begin{array}{*{20}{c}} {{v_1}} \\ \vdots \\ {{v_n}} \end{array}} \right],{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {\widehat x} \\ {\widehat y} \\ {\widehat {\textit{z}}} \end{array}} \right] . \end{split} 由于所有点都在圆周上, 距离基本相等, 可认为等权, 则有
{\boldsymbol{X}} = {\left( {{{\boldsymbol{B}}_1}^{\text{T}}{{\boldsymbol{B}}_1}} \right)^{ - 1}}{{\boldsymbol{B}}_1}^{\text{T}}{\boldsymbol{l}}. (5) 海底阵元坐标
\left({X}_{p}, {Y}_{p}, {Z}_{p}\right) 为\left[ {\begin{array}{*{20}{c}} {{X_p}}&{{Y_p}}&{{Z_p}} \end{array}} \right]_{}^{\text{T}} = \left[ {\begin{array}{*{20}{c}} {{X_0}}&{{Y_0}}&{{Z_0}} \end{array}} \right]_{}^{\text{T}} + \left[ {\begin{array}{*{20}{c}} {\widehat x}&{\widehat y}&{\widehat {\textit{z}}} \end{array}} \right]_{}^{\text{T}} . (6) 点位的协因数阵为
{{\boldsymbol{Q}}_{xx}} = \left[ {\begin{array}{*{20}{c}} {{Q_{\widehat X\widehat X}}}&{{Q_{\widehat X\widehat Y}}}&{{Q_{\widehat X\widehat Z}}} \\ {{Q_{\widehat Y\widehat X}}}&{{Q_{\widehat Y\widehat Y}}}&{{Q_{\widehat Y\widehat Z}}} \\ {{Q_{\widehat Z\widehat X}}}&{{Q_{\widehat Z\widehat Y}}}&{{Q_{\widehat Z\widehat Z}}} \end{array}} \right] = {\left( {{{\boldsymbol{B}}_1}^{\text{T}}{{\boldsymbol{B}}_1}} \right)^{ - 1}} . (7) 阵元点位精度可借助下式计算:
{\sigma _{\widehat X}} = {\sigma _0}\sqrt {{Q_{\widehat X\widehat X}}} ,\;\;{\sigma _{\widehat Y}} = {\sigma _0}\sqrt {{Q_{\widehat Y\widehat Y}}} ,\;\; {\sigma _{\widehat Z}} = {\sigma _0}\sqrt {{Q_{\widehat Z\widehat Z}}} . 1.2 传统相对测阵方法
海洋大地控制网布设完毕后, 利用圆走航标定获得初始位置和控制点之间的互测距获得距离测量值, 采用秩亏自由网平差处理, 对绝对标定后控制点进行坐标修正。
设海底控制网有m个控制点组成, 则全部基线数量为
{n_{{\text{all}}}} = \frac{{m\left( {m - 1} \right)}}{2}. (8) 根据给定的测距精度定权(
{\sigma }_{0} 为单位权标准差,{\sigma }_{\mathrm{i}} 为对应基线测距标准差):{P_i} = \frac{{\sigma _0^2}}{{\sigma _i^2}} . (9) 若第
k 条基线(共{n_{\rm all}} 条)的端点分别为{A}_{k} 和{B}_{k} , 令{\widehat X_{{A_k}}} = X_{{A_k}}^0 + {\widehat x_{{A_k}}}, \;{\widehat Y_{{A_k}}} = Y_{{A_k}}^0 + {\widehat y_{{A_k}}}, \;{\widehat Z_{{A_k}}} = Z_{{A_k}}^0 + {\widehat {\textit{z}}_{{A_k}}}, (10) {\widehat X_{{B_k}}} = X_{{B_k}}^0 + {\widehat x_{{B_k}}}, \;{\widehat Y_{{B_k}}} = Y_{{B_k}}^0 + {\widehat y_{{B_k}}}, \;{\widehat Z_{{B_k}}} = Z_{{B_k}}^0 + {\widehat {\textit{z}}_{{B_k}}}, (11) 误差方程为
\begin{split} {L_k} + {v_k} =& S_{{A_k}{B_k}}^0 + \frac{{\Delta X_{{A_k}{B_k}}^0}}{{S_{{A_k}{B_k}}^0}}({\widehat X_{{B_k}}} - {\widehat X_{{A_k}}}) + \frac{{\Delta Y_{{A_k}{B_k}}^0}}{{S_{{A_k}{B_k}}^0}}({\widehat Y_{{B_k}}} - {\widehat Y_{{A_k}}}) + \\&\frac{{\Delta Z_{{A_k}{B_k}}^0}}{{S_{{A_k}{B_k}}^0}}({\widehat Z_{{B_k}}} - {\widehat Z_{{A_k}}}),\\[-12pt] \end{split} (12) 其中,
\Delta X_{{A_k}{B_k}}^0 ,\Delta Y_{{A_k}{B_k}}^0 ,\Delta Z_{{A_k}{B_k}}^0 表示基线两端点各方向方向上坐标差值,S_{{A_k}{B_k}}^0 表示初值点下的基线长度。则有
{v_k} = {f_{{k_a}}}{\widehat x_{{A_k}}} + {f_{{k_b}}}{\widehat y_{{A_k}}} + {f_{{k_c}}}{\widehat {\textit{z}}_{{A_k}}} + {f_{{k_d}}}{\widehat x_{{B_k}}} + {f_{{k_e}}}{\widehat y_{{B_k}}} + {f_{{k_f}}}{\widehat {\textit{z}}_{{B_k}}} - {l_k}, (13) 其中,
{l_k} = {L_k} - S_{{A_k}{B_k}}^0 ,S_{{A_k}{B_k}}^0 = [ ( X_{B_k} - X_{A_k})^2 + ( Y_{B_k} - Y_{A_k} )^2 + ( Z_{B_k} - Z_{A_k} )^2 ]^{1/2} ,{f_{{k_a}}} = {{\Delta X_{{B_k}{A_k}}^0}} / {{S_{{A_k}{B_k}}^0}} ,{f_{{k_b}}} = {{\Delta Y_{{B_k}{A_k}}^0}} / {{S_{{A_k}{B_k}}^0}} ,{f_{{k_c}}} = {{\Delta Z_{{B_k}{A_k}}^0}} / {{S_{{A_k}{B_k}}^0}} ,{f_{{k_d}}} = {{\Delta X_{{A_k}{B_k}}^0}}/{{S_{{A_k}{B_k}}^0}} ,{f_{{k_e}}} = {{\Delta Y_{{A_k}{B_k}}^0}}/{{S_{{A_k}{B_k}}^0}} ,{f_{{k_f}}} = {{\Delta Z_{{A_k}{B_k}}^0}}/{{S_{{A_k}{B_k}}^0}} 。利用
{n_{{\text{all}}}} 条观测边, 有\left\{ \begin{gathered} {v_1} = {f_{{1_a}}}{{\widehat x}_{{A_1}}} + {f_{{1_b}}}{{\widehat y}_{{A_i}}} + {f_{{1_c}}}{{\widehat {\textit{z}}}_{{A_1}}} + {f_{{1_d}}}{{\widehat x}_{{B_1}}} + {f_{{1_e}}}{{\widehat y}_{{B_1}}} + {f_{{1_f}}}{{\widehat {\textit{z}}}_{{B_1}}} - {l_1}, \\ {v_2} = {f_{{2_a}}}{{\widehat x}_{{A_2}}} + {f_{{2_b}}}{{\widehat y}_{{A_2}}} + {f_{{2_c}}}{{\widehat {\textit{z}}}_{{A_2}}} + {f_{{2_d}}}{{\widehat x}_{{B_2}}} + {f_{{2_e}}}{{\widehat y}_{{B_2}}} + {f_{{2_f}}}{{\widehat {\textit{z}}}_{{B_2}}} - {l_2}, \\ {\text{ }}\begin{array}{*{20}{c}} \qquad \qquad \qquad \vdots \end{array}{\text{ }}\begin{array}{*{20}{c}} \vdots \end{array}{\text{ }}\begin{array}{*{20}{c}} \vdots \end{array} \\ {v_{{n_{{\text{all}}}}}} = {f_{{n_{{\text{all}}}}_a}}{{\widehat x}_{{A_{{n_{{\text{all}}}}}}}} + {f_{{n_{{\text{all}}}}_b}}{{\widehat y}_{{A_{{n_{{\text{all}}}}}}}} + {f_{{n_{{\text{all}}}}_c}}{{\widehat {\textit{z}}}_{{A_{{n_{{\text{all}}}}}}}} + {f_{{n_{{\text{all}}}}_d}}{{\widehat x}_{{B_{{n_{{\text{all}}}}}}}} + {f_{{n_{{\text{all}}}}_e}}{{\widehat y}_{{B_{{n_{{\text{all}}}}}}}} +\\\qquad {f_{{n_{{\text{all}}}}_f}}{{\widehat {\textit{z}}}_{{B_{{n_{{\text{all}}}}}}}} - {l_{{n_{{\text{all}}}}}}. \\ \end{gathered} \right. (14) 令S为约束条件矩阵, S的秩为d,
{{\boldsymbol{P}}_x} 为对应的权阵。重心基准约束下, 权阵为{{\boldsymbol{P}}_x} = {\boldsymbol{E}}, (15) {\boldsymbol{E}} 为单位矩阵, 为了获得未知参数的唯一解, 给定权的约束条件为{{\boldsymbol{S}}^{\text{T}}}{{\boldsymbol{P}}_x}{\boldsymbol{\widehat x}} = 0. (16) 当S的秩为d时, 有
r\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{{ B}}}_2}} \\ {{{\boldsymbol{S}}^{\text{T}}}} \end{array}} \right] = u. (17) 若有m个阵元点, 则自由测阵网平差中, 未知数的个数u = 3m。
根据
{\boldsymbol{NS}}{\boldsymbol{ = 0}}{\text{,}} (18) 令
{\alpha _i} 为矩阵N{\boldsymbol{ = B}}_{_2}^{\text{T}}{\boldsymbol{P}}{{\boldsymbol{B}}_2} 的第i 个零特征值对应的互不相关的特征向量, 则{\boldsymbol S}{{ = }}\left[ {\begin{array}{*{20}{c}} {{\alpha _1}}& \cdots &{{\alpha _d}} \end{array}} \right] 。基于式(14)构建平差模型:
{\boldsymbol{V}} = {{\boldsymbol{B}}_2}{\boldsymbol{\widehat x}} - {\boldsymbol{l}}, (19) 式中,
{\boldsymbol{V}} 的维数为{n_{{\text{sum}}}} \times 1 , 系数矩阵{{\boldsymbol{B}}_2} 的维数为{n_{{\text{all}}}} \times 3m ,{\boldsymbol{\widehat x}} 矩阵的维数为3m \times 1 ,l 的维数为{n_{{\text{all}}}} \times 1 。当{{\boldsymbol{V}}^{\text{T}}}{\boldsymbol{PV}} 最小时, 则有{{\boldsymbol{\widehat x}}_P} = {({{\boldsymbol{B}}_2}^{\text{T}}{\boldsymbol{P}}{{\boldsymbol{B}}_2} + {{\boldsymbol{P}}_x}{\boldsymbol{S}}{{\boldsymbol{S}}^{\text{T}}}{{\boldsymbol{P}}_x})^{ - 1}}{{\boldsymbol{B}}_2}^{\text{T}}{\boldsymbol{Pl}} . (20) 1.3 海底大地基准快速校准
海底大地基准快速校准是基于海面绝对位置校准和海底相对位置校准的一种标校方法, 其主要思路是利用部分基准点的绝对坐标和基准点间的距离测量值, 通过网平差处理后, 可获得海底控制网每个基准点的绝对坐标。
假设海底控制网有
m 个控制点, 其中通过水面标定获取绝对位置的控制点数目为n 。则未知基线数为{n_{{\text{sum}}}} = {{\left( {m + n - 1} \right)\left( {m - n} \right)} \mathord{\left/ {\vphantom {{\left( {m + n - 1} \right)\left( {m - n} \right)} 2}} \right. } 2}. (21) 由于部分控制点的绝对坐标通过水面标定已知, 所以基线可分为两类, 一种是一端控制点位置未知, 另一种是两端控制点位置均未知。前者数目为
{n_1} = n \left( {m - n} \right), (22) 后者数目为
{n_2} = {{\left( {m - n} \right) \left( {m - n - 1} \right)} \mathord{\left/ {\vphantom {{\left( {m - n} \right) \left( {m - n - 1} \right)} 2}} \right. } 2}. (23) 同样, 根据给定的测距精度定权(
{\sigma }_{0} 为单位权标准差,{\sigma }_{\mathrm{i}} 为对应基线测距标准差):{P_i} = \frac{{\sigma _0^2}}{{\sigma _i^2}}. (24) 若第
j 条双端未知控制点基线(共{n_2} 条)的端点分别为{A}_{j} 和{B}_{j} , 同式(10)和式(11), 可列误差方程为{L_j} + {v_j} = S_{{A_j}{B_j}}^0 + {f_{{j_a}}}\left( {{{\widehat x}_{{B_j}}} - {{\widehat x}_{{A_j}}}} \right) + {f_{{j_b}}}\left( {{{\widehat y}_{{B_j}}} - {{\widehat y}_{{A_j}}}} \right) + {f_{{j_c}}}\left( {{{\widehat {\textit{z}}}_{{B_j}}} - {{\widehat {\textit{z}}}_{{A_j}}}} \right). (25) 若第
i 条单端未知控制点基线(共{n_1} 条)的端点分别为{A_i} 和{B_i} , 其中{A_i} 为已知控制点, 令{\widehat X_{{A_i}}} = X_{{A_i}}^0,\;{\widehat Y_{{A_i}}} = Y_{{A_i}}^0,\;{\widehat Z_{{A_i}}} = Z_{{A_i}}^0, (26) {\widehat X_{{B_i}}} = X_{{B_i}}^0 + {\widehat x_{{B_i}}},\;{\widehat Y_{{B_i}}} = Y_{{B_i}}^0 + {\widehat y_{{B_i}}},\;{\widehat Z_{{B_i}}} = Z_{{B_i}}^0 + {\widehat {\textit{z}}_{{B_i}}}. (27) 同理可列误差方程:
{L_i} + {v_i} = S_{{A_i}{B_i}}^0 + {f_{{i_a}}}{\widehat x_{{B_i}}} + {f_{{i_b}}}{\widehat y_{{B_i}}} + {f_{{i_c}}}{\widehat {\textit{z}}_{{B_i}}}, (28) 则利用
{n_{{\text{sum}}}} 条未知基线, 有\left\{ \begin{array}{*{20}{l}} {v_1} = - {f_{{1_a}}}{{\widehat x}_{{A_1}}} - {f_{{1_b}}}{{\widehat y}_{{A_1}}} - {f_{{1_c}}}{{\widehat {\textit{z}}}_{{A_1}}} + {f_{{1_a}}}{{\widehat x}_{{B_1}}} +\\\qquad {f_{{1_b}}}{{\widehat y}_{{B_1}}} + {f_{{1_c}}}{{\widehat {\textit{z}}}_{{B_1}}} - {l_1}, \\ \qquad\qquad \vdots \\ {v_{{n_2}}} = - {f_{{n_2}_a}}{{\widehat x}_{{A_{{n_2}}}}} - {f_{{n_2}_b}}{{\widehat y}_{{A_{{n_2}}}}} - {f_{{n_2}_c}}{{\widehat {\textit{z}}}_{{A_{{n_2}}}}} + \\\qquad{f_{{n_2}_a}}{{\widehat x}_{{B_{{n_2}}}}} + {f_{{n_2}_b}}{{\widehat y}_{{B_{{n_2}}}}} + {f_{{n_2}_c}}{{\widehat {\textit{z}}}_{{B_{{n_2}}}}} - {l_{{n_2}}}, \\ {v_{{n_2} + 1}} = {f_{{(n_2 + 1)_a}}}{{\widehat x}_{{A_{{n_2} + 1}}}} + {f_{{(n_2 + 1)_b}}}{{\widehat y}_{{A_{{n_2} + 1}}}} + {f_{{(n_2 + 1)_c}}}{{\widehat {\textit{z}}}_{{A_{{n_2} + 1}}}} + {f_{{(n_2 + 1)_a}}}{{\widehat x}_{{B_{{n_2} + 1}}}} +\\\qquad {f_{{(n_2 + 1)_b}}}{{\widehat y}_{{B_{{n_2} + 1}}}} + {f_{{(n_2 + 1)_c}}}{{\widehat {\textit{z}}}_{{B_{{n_2} + 1}}}} - {l_{{n_2} + 1}}, \\ \qquad\qquad \vdots \\ {v_{{n_{{\text{sum}}}}}} = {f_{{n_{{\text{sum}}}}_a}}{{\widehat x}_{{A_{{n_{{\text{sum}}}}}}}} + {f_{{n_{{\text{sum}}}}_b}}{{\widehat y}_{{A_{{n_{{\text{sum}}}}}}}} + {f_{{n_{{\text{sum}}}}_c}}{{\widehat {\textit{z}}}_{{A_{{n_{{\text{sum}}}}}}}} + {f_{{n_{{\text{sum}}}}_a}}{{\widehat x}_{{B_{{n_{{\text{sum}}}}}}}} +\\\qquad {f_{{n_{{\text{sum}}}}_b}}{{\widehat y}_{{B_{{n_{{\text{sum}}}}}}}} + {f_{{n_{{\text{sum}}}}_c}}{{\widehat {\textit{z}}}_{{B_{{n_{{\text{sum}}}}}}}} - {l_{{n_{{\text{sum}}}}}} , \end{array} \right. (29) {l_i} = {L_i} - S_{{A_i}{B_i}}^0. (30) 当控制点数目较少, 导致方程组秩亏时, 采用重心基准作为额外约束, 同1.2节可得基准约束条件矩阵S。
基于式(29)构建平差模型:
{\boldsymbol{V}} = {{\boldsymbol{B}}_3}{\boldsymbol{\widehat x}} - {\boldsymbol{l}}, (31) 式中,
{\boldsymbol{V}} 的维数为{n_{{\text{sum}}}} \times 1 , 系数矩阵{{\boldsymbol{B}}_3} 的维数为{n_{sum}} \times 3(m - n) ,{\boldsymbol{\widehat x}} 矩阵的维数为3\left( {m - n} \right) \times 1 ,\boldsymbol{l} 的维数为{n_{{\text{sum}}}} \times 1 。当{{\boldsymbol{V}}^{\text{T}}}{\boldsymbol{PV}} 最小, 且{\text{rank}}({{\boldsymbol{B}}_3}) < 3(m - n) 时, 有{{\boldsymbol{\widehat x}}_P} = {({{\boldsymbol{B}}_3}^{\text{T}}{\boldsymbol{P}}{{\boldsymbol{B}}_3} + {{\boldsymbol{P}}_x}{\boldsymbol{S}}{{\boldsymbol{S}}^{\text{T}}}{{\boldsymbol{P}}_x})^{ - 1}}{{\boldsymbol{B}}_3}^{\text{T}}{\boldsymbol{Pl}}. (32) 当
{\text{rank}}({{\boldsymbol{B}}_3}) \geqslant 3(m - n) 时, 有{{\boldsymbol{\widehat x}}_P} = {({{\boldsymbol{B}}_3}^{\text{T}}{\boldsymbol{P}}{{\boldsymbol{B}}_3})^{ - 1}}{{\boldsymbol{B}}_3}^{\text{T}}{\boldsymbol{Pl}}. (33) 获取基线长度的改正值, 以及阵元点坐标的改正值:
{\boldsymbol{\widehat L}} = {\boldsymbol{L}} + {\boldsymbol{V}} ,{\boldsymbol{\widehat X}} = {\boldsymbol{X}} + {\boldsymbol{\widehat x}} 。精度为\sigma _0^{^2} = \frac{{{{\boldsymbol{V}}^{\text{T}}}{\boldsymbol{PV}}}}{{{n_{{\text{sum}}}} - {\text{rank}}({{\boldsymbol{B}}_3})}}. (34) 2. 仿真分析
为了初步验证本文提出的海底大地基准快速标校法的可行性, 拟在不同阵型、不同标定方案下进行仿真实验。比较海底海面快速校准与单纯相对测阵的区别。
仿真实验中不同阵型的真实位置(圆走航标定结果)如图2所示, 各阵型均为正多边形, 圆半径为1000 m, 基阵中心为坐标原点。实际布放常用GNSS接收机的定位精度一般为5 mm+0.5 ppm左右, 而深度计的标称精度一般为(0.01 ± 0.1%) m[20-21], 但是考虑到布放时信标的漂移, 仿真过程中会对假定未被圆走航标定的基元增加标准差
\sigma 为10 m正态分布的随机平面位置误差和标准差\sigma 为1 m正态分布的随机深度位置误差, 模拟海底控制网布设时只对部分控制点进行海面圆走航校准的情形。仿真时所有基元间的测距信息L 增加了标准差为距离千分之五大小正态分布的随机测距误差, 且不同基元间的测距次数为50次。仿真时将坐标真值作为外符合参考; 各个边的观测条件一致, 采用距离定权:{P_i} = \frac{1}{{{S_i}}}. (35) 2.1 绝对标定控制点数目对仿真结果的影响
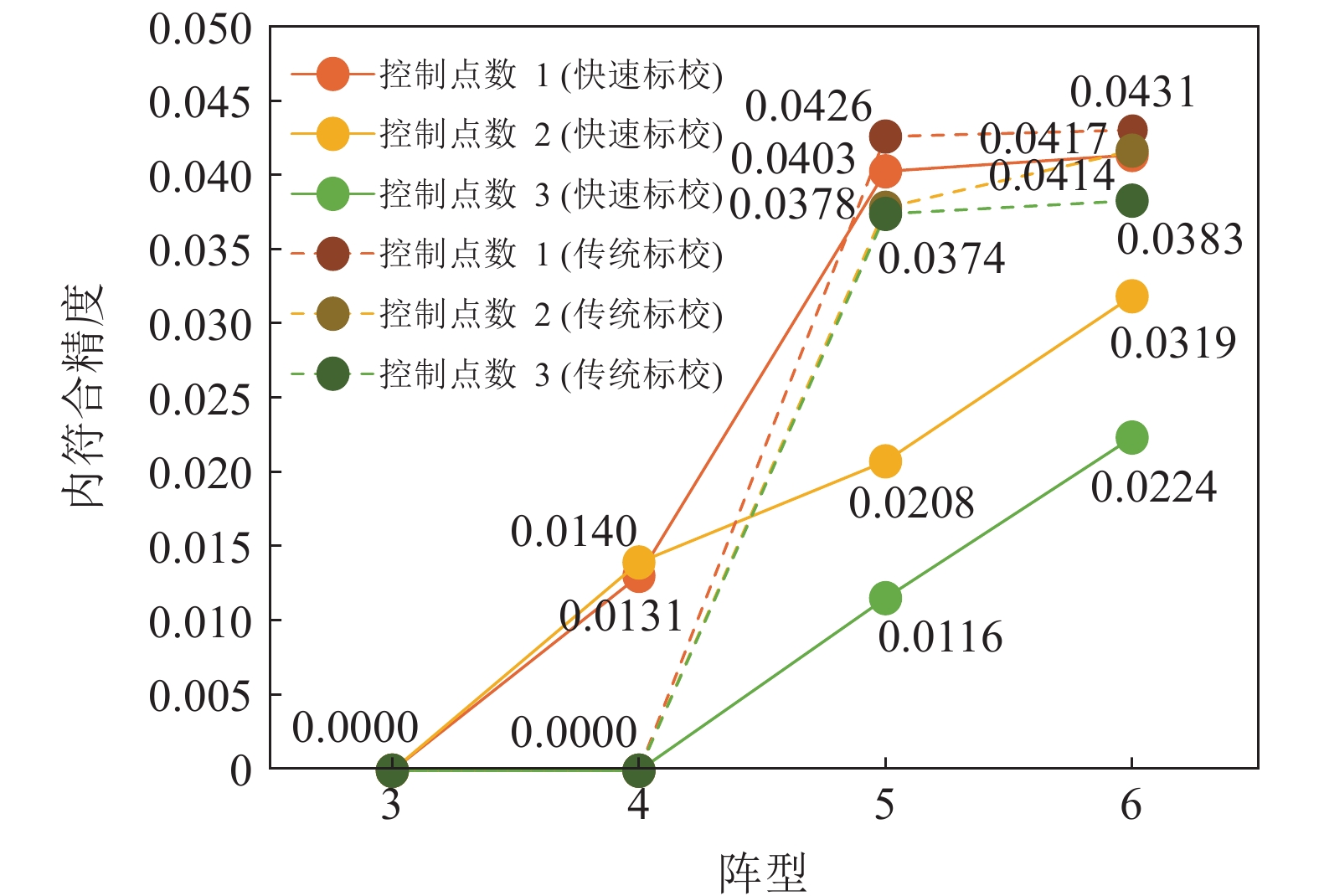
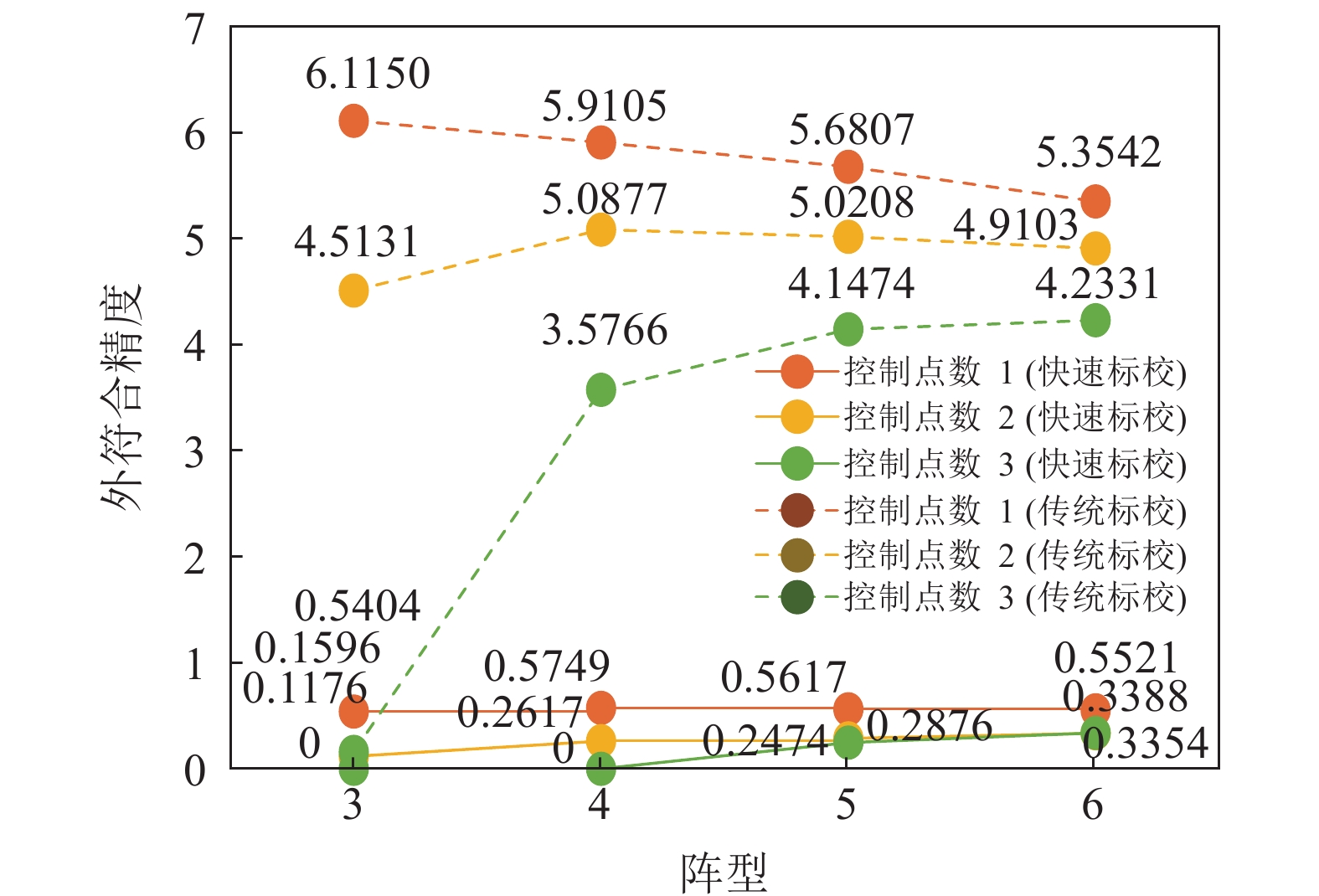
海面圆走航绝对标定的控制点数目不同的情况下, 不同阵型的整体校准结果对比如图3和图4所示, 具体结果见表1。
表 1 不同阵型下各布设方案的精度对比结果控制点数 阵型 海底海面快速校准 传统相对测阵平差 内符合精度 (m) 外符合精度 (m) 内符合精度 (m) 外符合精度 (m) 1 3 0.00 0.54 0.00 6.12 4 0.01 0.57 0.00 5.91 5 0.04 0.56 0.04 5.68 6 0.04 0.55 0.04 5.35 2 3 0.00 0.12 0.00 4.51 4 0.01 0.26 0.00 5.09 5 0.02 0.29 0.048 5.02 6 0.03 0.34 0.04 4.91 3 3 0.00 0.00 0.00 0.16 4 0.00 0.00 0.00 3.58 5 0.01 0.25 0.04 4.15 6 0.02 0.33 0.04 4.23 从图3可知, 海面海底快速校准的外符合精度, 在各方案下均远优于传统相对测阵平差的结果, 达到分米级。且绝对标定的控制点数目大于等于2时, 阵元数目越高, 快速校准的内符合精度优势越大, 达到厘米级。仿真实验表明, 快速校准方法的外符合精度达到分米级, 而对于内符合精度来说, 控制点数目为2或3时, 趋势接近, 无明显提升。出于工程考虑, 绝对控制点数目越低越好, 但校准数目为1时, 精度相对较低, 所以选择校准点数目为2的方案作进一步分析。
2.2 绝对标定控制点分布对仿真结果的影响
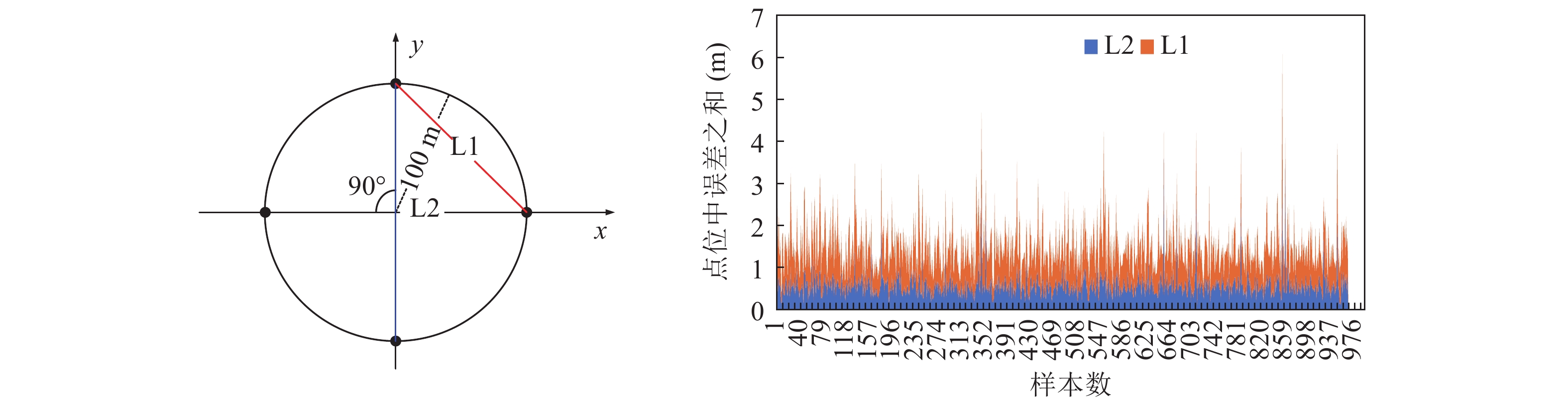
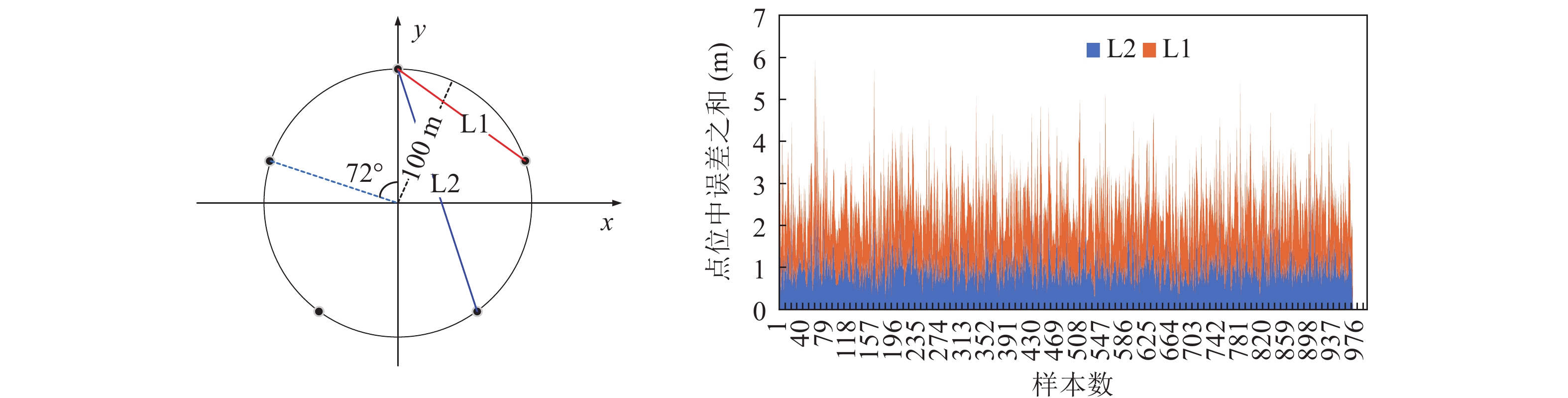
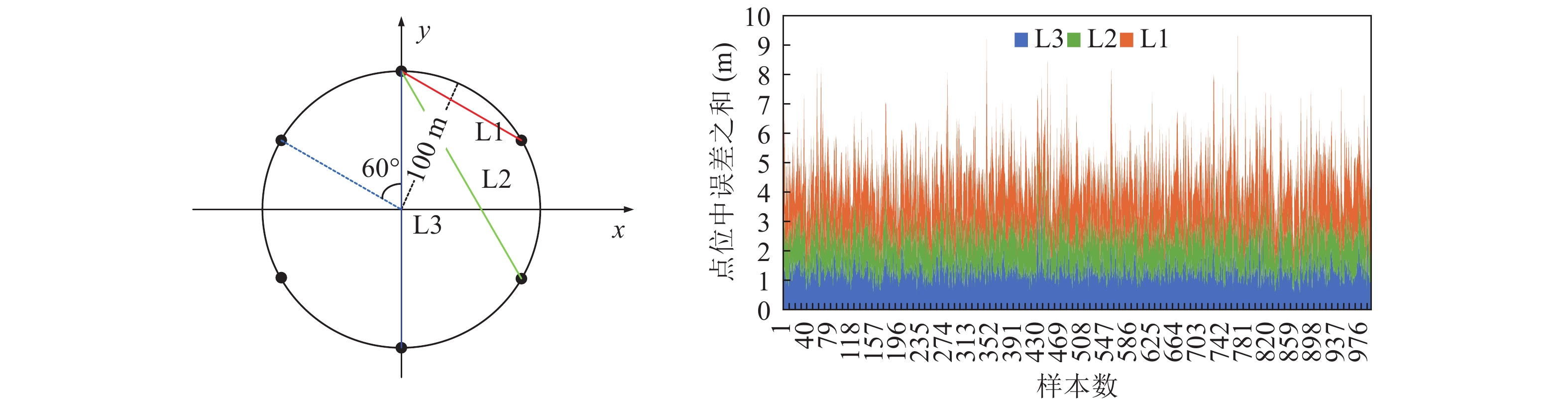
本节在海面绝对标定控制点数目为2的前提下, 对不同网型下的不同控制点分布进行仿真分析, 探究在不同网型中控制点的最优分布。仿真条件不变, 绝对标定控制点数目为2, 进行1000次的蒙特卡洛仿真实验, 各阵型在不同分布下的校准结果如图5—图7所示。由于三元阵在此没有分布差异, 所以不做比较。
如图5—图7所示, L1~L3分别对应左图中在该阵型下选取的不同校准方案, 方案选取对应基线两端控制点进行绝对标定。右图为1000次仿真结果的所有控制点的整体水平位置校准误差。从图中可以看出, 对于同一网型, 基线越短时校准误差越大, 即当起算基线相对阵型越长, 解算精度越高。为了更加直观地看出基线长度和校准误差水平的关系, 将所有1000次仿真结果取均值进行比较, 结果进一步验证了该结论, 如表2所示, 平均点位中误差
\delta 不高于0.5 m,表 2 基线长度与定位误差的关系网型 方案 基线长度 (m) \delta (m) 四元阵 {{\rm{L}}1} 1414.335 0.48 {{\rm{L}}2} 2000.400 0.37 五元阵 {{\rm{L}}1} 1175.741 0.49 {{\rm{L}}2} 1902.534 0.34 六元阵 {{\rm{L}}1} 1000.200 0.46 {{\rm{L}}2} 1732.513 0.34 {{\rm{L}}3} 2000.900 0.33 \delta = \frac{1}{n}\left( {\sum\limits_{i = 1}^n {\sqrt[{}]{{{{({{\widehat X}_i} - {X_i})}^2} + {{({{\widehat Y}_i} - {Y_i})}^2} + {{({{\widehat Z}_i} - {Z_i})}^2}}}} } \right), (38) 其中,
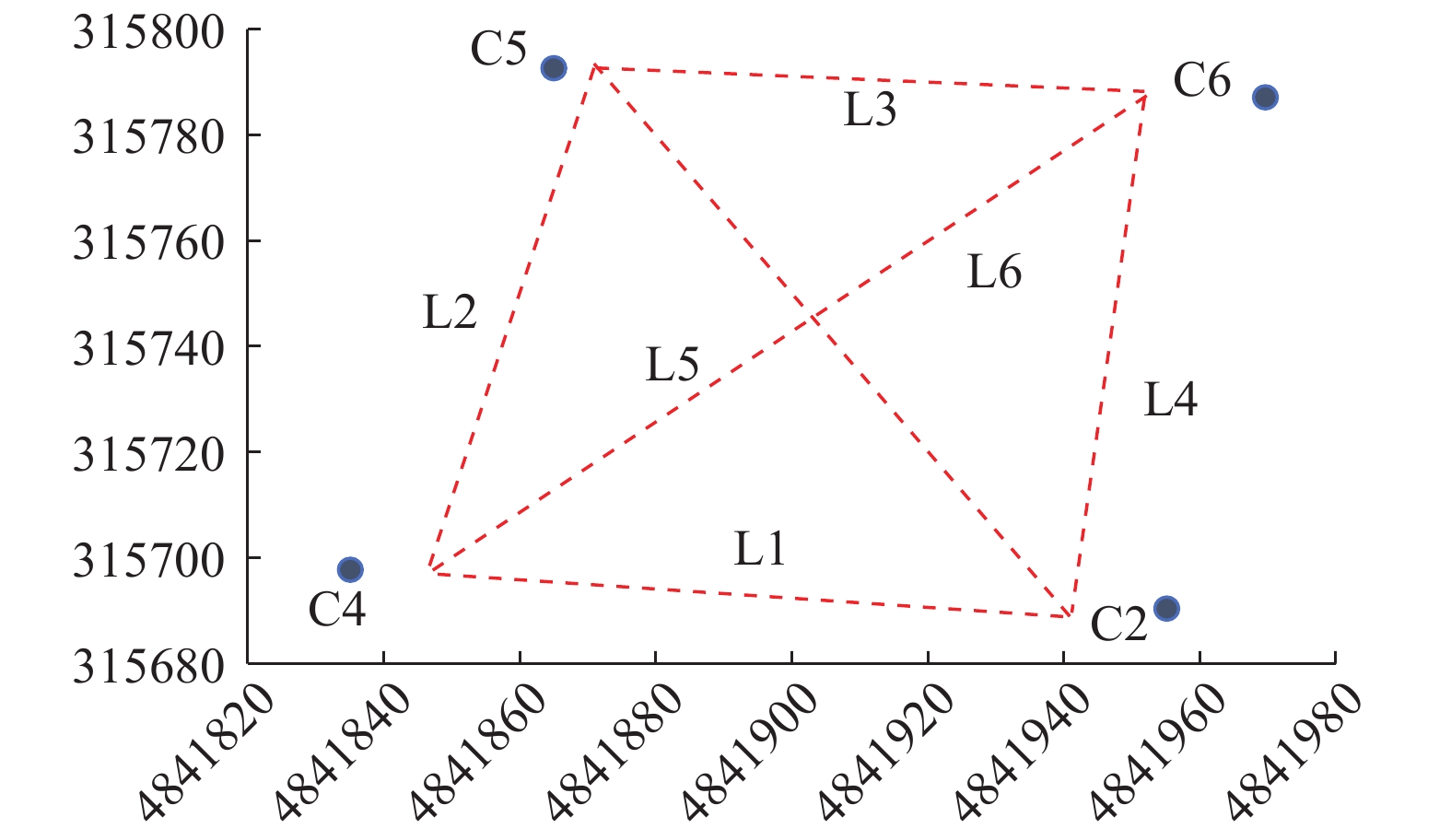
({\widehat X_i},{\widehat Y_i},{\widehat Z_i}) 表示阵元i 位置估计值,({X_i},{Y_i},{Z_i}) 表示阵元i 位置真值,n 表示阵元数目。当起算基线越长时, 以该基线为约束的网平差方程组条件数越低, 解算精度越高。
2.3 不同网型的总体校准方案
从仿真结果来说, 单个阵型中所需要的控制点数目为2, 但是组网时, 控制点是可以复用的。只需要满足单个三元或四元阵中包含2个控制点即可。再考虑到基线长度和对称性, 拟定了一些在不同网型下, 总体控制点数目最少的方案[22-23]。
图8中红色阵元为选定的绝对标定点。对于正三边形网型, 在使用本文提出的海底海面快速校准方法时可以节省1/3的校准资源; 对于正四边形网可节省1/2的校准资源; 对于正六边形网可节省2/3的校准资源。阵元越多, 使用联合标校方法节省的校准资源越多。
3. 湖试试验及数据处理分析
为进一步验证本文提出的海底大地基准快速标校法及其相应的校准方案的正确性, 于吉林省吉林市松花湖进行了四元阵控制网布设实验, 试验水深约60 m。试验条件所限, 无法进行大范围布网, 仅对单个四元阵进行定位精度和导航精度验证。若单阵校准后定位与导航精度满足要求, 则整体控制网由于作用范围内阵元数目的增加, 其定位导航精度亦将满足要求。
实验共设计了4套锚系阵元, 布放在湖底组成控制网, 阵元之间的距离设计为100 m左右。通过配备GNSS的实验船将阵元布设到湖底, 投放时记录实验船GPS位置, 作为阵元的位置初值。根据记录位置开展圆走航标校试验和湖底基阵的相对测量, 阵元间基线往返观测50次。在完成控制网布放和标定试验后, 利用布放的4只阵元开展定位导航试验。由实验船携带声学基阵模拟目标在控制网范围内的运动, 同时在定位过程中记录船载基阵上方架设的GNSS接收机(Veripos LD7, 其精密单点定位精度 < 0.1 m)的实时位置信息, 作为定位精度评价参考值。
3.1 不同快速校准方案的阵元校准结果
为充分验证该文的理论方法, 对所有阵元进行了圆走航标校观测。在验证快速校准方法时, 其中两个阵元使用圆走航绝对标定后的坐标, 其余阵元使用布设时记录GPS值作为水平位置, 取平均水深为垂直位置。如表3所示, 表中记录了各个控制点投放时水面船的GPS位置作为初值, 圆走航标定结果作为修正值。可以看到C2和C4平面位置差相对较大, 主要原因有两点: (1) 信标在后续试验中移动过位置, 但是通过拖拽水面锚系的方式移动, 无法确定信标位置, 所以并未重新记录初值; (2) 布放采用的是锚系结构, 本身绳长为10 m左右, 随水流会有漂动。
表 3 各信标标定结果信标编号 X (m) Y (m) Z (m) C2 初值 4841929.578 315676.980 62.828 修正后 4841955.114 315690.413 60.955 C4 初值 4841854.225 315692.535 60.882 修正后 4841835.066 315697.764 59.964 C5 初值 4841862.234 315789.482 61.837 修正后 4841864.983 315792.608 59.834 C6 初值 4841958.240 315783.367 61.581 修正后 4841969.620 315787.096 60.562 湖底控制网网型如图9所示, 为比较不同校准方案下的校准结果, 分别选取L1~L6方案节点为绝对标定点, 其余点仅使用投放时记录的位置信息作为已知值进行快速校准。
圆走航模式下, 测距系统误差对水平位置分量影响较小, 若采用历元差分模型更可以消除大部分系统误差, 在3000 m水深试验中定位精度高达0.2 m。因此, 本文将圆走航标校值作为参考真值, 将同一校准方案下不同阵元的点位中误差平均值
\delta 作为外符合精度评价标准, 比较不同方案下的整体校准精度和对应基线长度的关系。如表4所示, N, E, U是联合标校结果与各阵元的圆走航标校结果在各方向上的均方根误差。可以发现快速校准在高程方向上与绝对校准相差较大, 这可能是绝对校准本身在高程方向上误差较大导致的, 联合标校方法引入了相对测量值, 对声速误差不敏感, 其自身的高程方向的精度应当更高。但由于海底基线标校对高程方向不敏感, 导致平差方程的病态。可以考虑在基阵网布设时适量加入深度值相差较大的阵元, 如浮标潜标等, 既方便绝对校准, 也可一定程度上克服方程的病态。
表 4 各方案标校精度对比方案 基线长度 (m) N (RMSE) (m) E (RMSE) (m) U (RMSE) (m) 外符合精度( \delta ) (m) 内符合精度( \sigma _0^{} ) (m) L1 120.277 0.024 0.111 3.253 0.202 0.081 L2 99.451 0.051 0.087 3.822 0.127 0.570 L3 104.785 0.172 0.280 6.058 0.632 0.031 L4 97.766 0.151 0.195 4.163 0.493 0.030 L5 136.267 0.074 0.031 3.904 0.134 0.112 L6 161.510 0.093 0.049 3.001 0.209 0.017 从水平误差来说, 虽然精度水平没有按照预估中与基线长度成反比, 但可能是数据量较小导致。总体上各点点位中误差之和最佳情况下低于0.2 m, 单个阵元平均误差低于0.05 m。从结果来说, 利用部分基元的绝对校准实现了对基阵网的整体精准校准。
3.2 海底海面快速校准方法导航性能验证
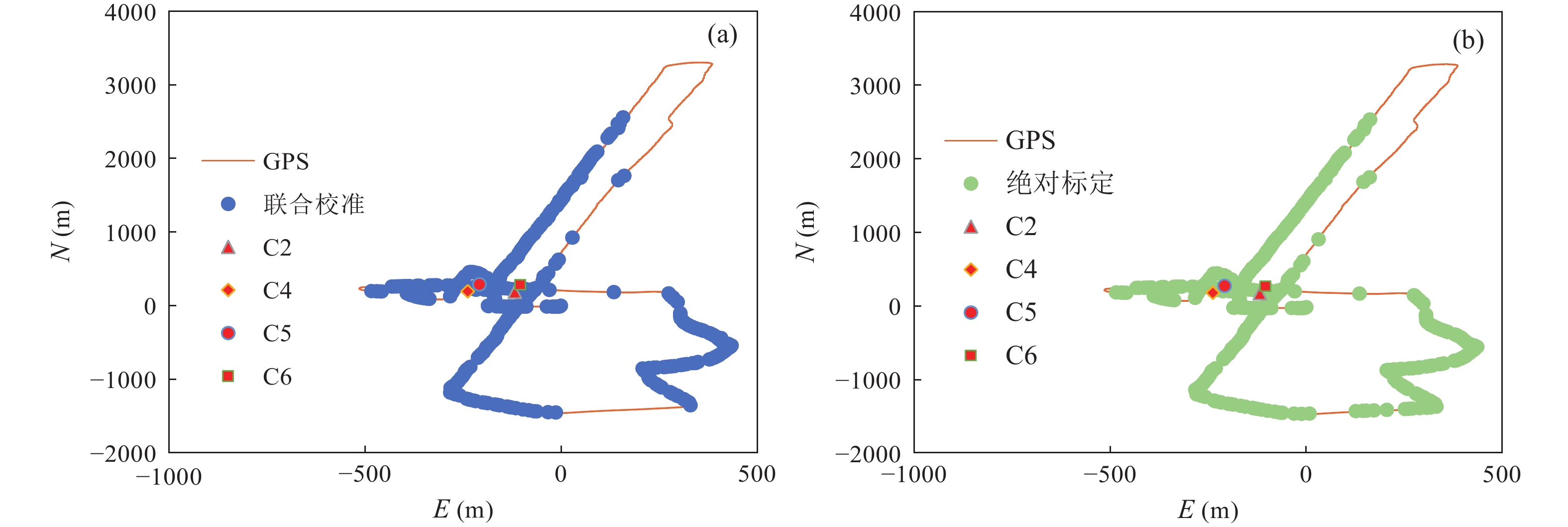
如图10和图11所示分别将全部阵元绝对标定方法和海底海面快速校准方法下(2.1节提出的方案)标定的控制网定位结果与GPS轨迹对比, 由于用户运动轨迹大部分在控制网外, 导致定位结果较差, 但在认定GPS值为真值的情况下, 两者具有相同量级的定位精度, 水平定位结果相差小于5 m, 本文提出的海底海面快速校准方法达到了预期要求。
3.3 试验总结
海底大地基准快速标校法的优点在于, 在海洋大地控制网布设时, 仅需要对小部分基准点进行水面标定获得精确位置信息, 通过基准点之间的相对测量信息, 即可获取全部的控制网基准点的精密位置, 提高了标定效率。大部分情况下其定位精度量级不低于对全部基准点进行水面标定, 相较于传统相对测阵方法拥有更好的外符合精度。
现有方法下, 绝对标定与相对测阵所需要测量的参数和联合标校需要的参数是一致的。联合标校的优点在于减少绝对标校的信标点数, 降低工程量, 且定位性能不低于原方法, 在绝对位置精度上还有一定提升。
综上, 湖试结论对实际海洋大范围布设, 依旧具备一定的参考价值。
4. 结论
海洋大地控制网布设是海洋事业进一步发展的重要基础与保障, 在海图测绘、需要高精度定位的水下工程作业、地壳运动关键节点的动态监测等方面都有着重要意义。但繁琐的标定作业和阵型精度修正, 严重限制了控制网的布设进程。本文提出海底海面联合标定方法, 利用小部分控制点的绝对标定信息和控制点的互测距信息完成所有控制点位置标定的同时进行阵型的修正。通过定期的相互测量和少量的绝对标定即可保持控制网阵型的相对精度。
与传统方法相比, 本文方法在保证标校精度不降低的条件下, 标定作业效率提升50%以上。通过网平差方法融合了互测距信息和绝对标定信息, 阵型绝对坐标修正精度从米级提升至分米级, 定位结果一致性更强。分析60 m水深的湖试数据, 当基线长度为100 m左右, 以绝对标定结果为参考真值时, 点位中误差之和低于0.2 m, 内符合精度最高可达到厘米级别。当其应用于深水标定作业时, 标定作业效率随着标定作业工程量的提升也会进一步提高。仿真理论分析和实验数据表明本文方法能够实现高精度和高效率的控制网阵型标定和修正, 解决了现有海洋大地控制网布设效率低、位置精度维护困难的问题, 具有一定的应用价值。目前实测数据仅采用湖试结果, 对于实际海底大地基准布设而言, 条件要苛刻得多。本文方法的适用性与可靠性仍需要进一步研究。
-
表 1 不同阵型下各布设方案的精度对比结果
控制点数 阵型 海底海面快速校准 传统相对测阵平差 内符合精度 (m) 外符合精度 (m) 内符合精度 (m) 外符合精度 (m) 1 3 0.00 0.54 0.00 6.12 4 0.01 0.57 0.00 5.91 5 0.04 0.56 0.04 5.68 6 0.04 0.55 0.04 5.35 2 3 0.00 0.12 0.00 4.51 4 0.01 0.26 0.00 5.09 5 0.02 0.29 0.048 5.02 6 0.03 0.34 0.04 4.91 3 3 0.00 0.00 0.00 0.16 4 0.00 0.00 0.00 3.58 5 0.01 0.25 0.04 4.15 6 0.02 0.33 0.04 4.23 表 2 基线长度与定位误差的关系
网型 方案 基线长度 (m) \delta (m) 四元阵 {{\rm{L}}1} 1414.335 0.48 {{\rm{L}}2} 2000.400 0.37 五元阵 {{\rm{L}}1} 1175.741 0.49 {{\rm{L}}2} 1902.534 0.34 六元阵 {{\rm{L}}1} 1000.200 0.46 {{\rm{L}}2} 1732.513 0.34 {{\rm{L}}3} 2000.900 0.33 表 3 各信标标定结果
信标编号 X (m) Y (m) Z (m) C2 初值 4841929.578 315676.980 62.828 修正后 4841955.114 315690.413 60.955 C4 初值 4841854.225 315692.535 60.882 修正后 4841835.066 315697.764 59.964 C5 初值 4841862.234 315789.482 61.837 修正后 4841864.983 315792.608 59.834 C6 初值 4841958.240 315783.367 61.581 修正后 4841969.620 315787.096 60.562 表 4 各方案标校精度对比
方案 基线长度 (m) N (RMSE) (m) E (RMSE) (m) U (RMSE) (m) 外符合精度( \delta ) (m) 内符合精度( \sigma _0^{} ) (m) L1 120.277 0.024 0.111 3.253 0.202 0.081 L2 99.451 0.051 0.087 3.822 0.127 0.570 L3 104.785 0.172 0.280 6.058 0.632 0.031 L4 97.766 0.151 0.195 4.163 0.493 0.030 L5 136.267 0.074 0.031 3.904 0.134 0.112 L6 161.510 0.093 0.049 3.001 0.209 0.017 -
[1] Spiess F N, Chadwell C D, Hildebrand J A, et al. Precise GPS/Acoustic positioning of seafloor reference points for tectonic studies. Phys. Earth Planet. Inter., 1998; 108(2): 101—112 DOI: 10.1016/S0031-9201(98)00089-2
[2] Favali P, Beranzoli L. Seafloor observatory science: A review. Ann. Geophys., 2006; 49(2-3): 515—567 DOI: 10.4401/ag-3125
[3] Matsumoto Y, Ishikawa T, Fujita M. Weak interplate coupling beneath the subduction zone off Fukushima, NE Japan, inferred from GPS/acoustic seafloor geodetic observation. Earth Planets Space, 2008; 60(6): 9—12 DOI: 10.1186/BF03353114
[4] Mochizuki M, Sato M, Yoshida Z, et al. Seafloor geodetic observations around Japan. Proceedings of the 2002 Interntional Symposium on Underwater Technology, IEEE, Tokyo, Japan, 2002: 239—243
[5] Fujita M, Ishikawa T, Mochizuki M, et al. GPS/Acoustic seafloor geodetic observation: method of data analysis and its application. Earth Planets Space, 2006; 58(3): 265—275 DOI: 10.1186/BF03351923
[6] 吴永亭. LBL精密定位理论方法研究及软件系统研制. 博士学位论文, 武汉: 武汉大学, 2013 [7] Vickery K. Acoustic positioning systems: New concepts − the future. Proceedings of the 1998 Workshop on Autonomous Underwater Vehicles, IEEE, Cambridge, MA, USA, 1998: 103—110
[8] Larsen M B. Synthetic long baseline navigation of underwater vehicles. OCEANS 2000 MTS/IEEE Conference and Exhibition, IEEE, Providence, RI, USA, 2000: 2043—2050
[9] Sato M, Fujita M, Matsumoto Y, et al. Improvement of GPS/acoustic seafloor positioning precision through controlling the ship's track line. J. Geodesy, 2013; 87(9): 825—842 DOI: 10.1007/s00190-013-0649-9
[10] 韩云峰, 郑翠娥, 孙大军. 长基线定位系统高精度阵型标定方法. 声学学报, 2016; 41(4): 456—464 DOI: 10.15949/j.cnki.0371-0025.2016.04.002 [11] 赵建虎, 邹亚靖, 吴永亭, 等. 深度约束的海底控制网点坐标确定方法. 哈尔滨工业大学学报, 2016; 48(10): 137—141 DOI: 10.11918/j.issn.0367-6234.2016.10.020 [12] 赵建虎, 陈鑫华, 吴永亭, 等. 顾及波浪影响和深度约束的水下控制网点绝对坐标的精确确定. 测绘学报, 2018; 47(3): 413—421 DOI: 10.11947/j.AGCS.2018.20170246 [13] Han G, Qian A, Zhang C, et al. Localization algorithms in large-scale underwater acoustic sensor networks: A quantitative comparison. Int. J. Distrib. Sens. Netw., 2014; 2014(1): 1—11 DOI: 10.1155/2014/379382
[14] 刘宁, 徐天河. 基于自适应分层的声线跟踪改进算法. 中国卫星导航年会, 中国卫星导航学术年会组委会, 北京, 2019: 74—78 [15] Osada Y, Kido M, Fujimoto H. A long-term seafloor experiment using an acoustic ranging system: Precise horizontal distance measurements for detection of seafloor crustal deformation. Ocean Eng., 2012; 51: 28—33 DOI: 10.1016/j.oceaneng.2012.05.006
[16] Zhao J, Zou Y, Zhang H, et al. A new method for absolute datum transfer in seafloor control network measurement. J. Mar. Sci. Technol., 2016; 21: 226 DOI: 10.1007/s00773-015-0344-z
[17] 赵建虎, 李娟娟, 李萌. 海洋测量的进展及发展趋势. 测绘信息与工程, 2009; 34(4): 25—27 [18] 杨元喜, 刘焱雄, 孙大军, 等. 海底大地基准网建设及其关键技术. 中国科学: 地球科学, 2020; 50(7): 936—945 DOI: 10.1360/SSTe-2019-0242 [19] 曾安敏, 杨元喜, 明锋, 等. 海底大地基准点圆走航模式定位模型及分析. 测绘学报, 2021; 50(7): 939—952 DOI: 10.11947/j.AGCS.2021.20200529 [20] BalluV, Bouin M N, Calmant S, et al. Absolute seafloor vertical positioning using combined pressure gauge and kinematic GPS data. J. Geod., 2010; 84(1): 65—77 DOI: 10.1007/s00190-009-0345-y
[21] Sharp I, Yu K, Hedley M. On the GDOP and accuracy for indoor positioning. IEEE Trans. Aerosp. Electron. Syst., 2012; 48(3): 2032—2051 DOI: 10.1109/TAES.2012.6237577
[22] Osada Y, Kido M, Fujimoto H, et al. Development of a seafloor acoustic ranging system toward the seafloor cable network system. Ocean Eng., 2008; 35(14-15): 1401—1405 DOI: 10.1016/j.oceaneng.2008.07.007
[23] 韩云峰. 大规模水下传感器网络节点精确定位技术研究. 博士学位论文, 哈尔滨: 哈尔滨工程大学, 2016 -
期刊类型引用(1)
1. 张旭,李万鹏. 跨介质出水航行器水下信息获取技术发展与展望. 水下无人系统学报. 2024(04): 659-667 .  百度学术
百度学术
其他类型引用(0)



 下载:
下载: