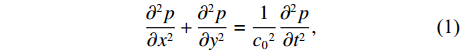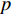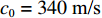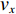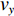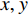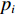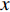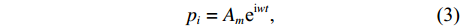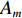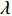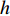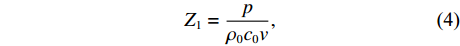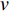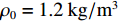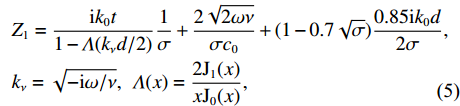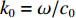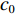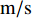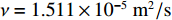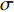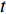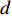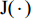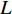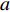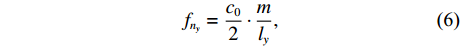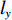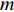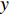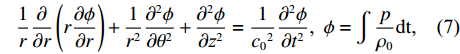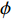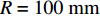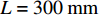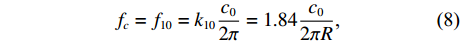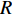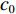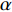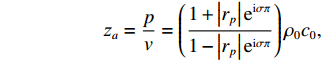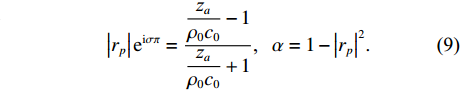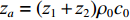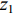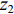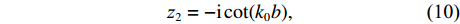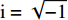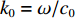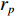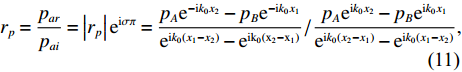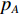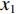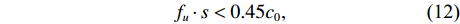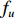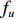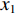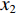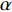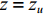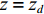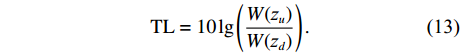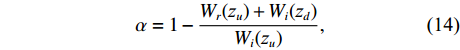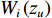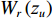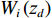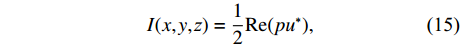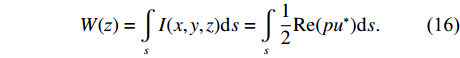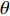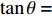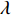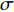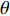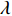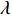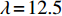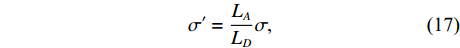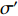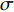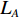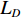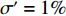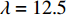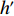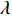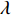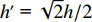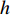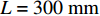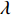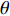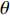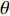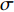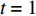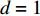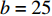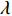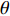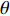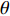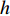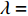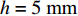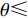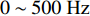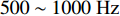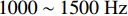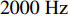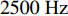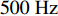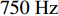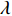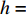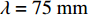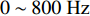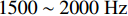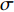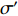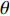波纹穿孔板吸声特性研究

刘传洋; 王晓宇; 张光宇; 孙晓峰

doi:10.15949/j.cnki.0371-0025.2023.03.012

波纹穿孔板吸声特性研究

1.
北京航空航天大学航空发动机研究院　北京　102206
2.
北京航空航天大学能源与动力工程学院　北京　102206

基金项目: 国家科技重大专项 (2017-II-003-0015)和航空科学基金项目(2019ZB051001)资助

详细信息

通讯作者:
刘传洋, liuchuanyang@buaa.edu.cn

PACS:
计量
- 文章访问数: 233
- HTML全文浏览量: 20
- PDF下载量: 43
出版历程
- 收稿日期: 2022-04-14
- 修回日期: 2022-08-11
- 网络出版日期: 2023-05-07
- 刊出日期: 2023-05-10

Research on sound absorption characteristics of corrugated perforated plate

1.
Research Institute of Aero-Engine, Beihang University　Beijing　102206
2.
School of Energy and Power Engineering, Beihang University　Beijing　102206

摘要

摘要:
研究了平面波垂直入射和掠入射两种情况下波纹穿孔板对声波的耗散作用, 结果表明在这两种情况下波纹穿孔板的声学特性都有别于平板穿孔板。在垂直入射条件下, 通过“等效穿孔率”可以在中、低频率范围内使波纹穿孔板和平板穿孔板的吸声特性“重合”。波纹穿孔板在高频范围会出现异于平板穿孔板的双尖峰现象, 进一步研究发现这是由波纹板形状导致的背腔深度的连续变化所引起的。在掠入射条件下, 波纹穿孔板与平板穿孔板无法通过“等效穿孔率”替代。波纹穿孔板的板高和板长对其声学性能都有明显影响, 当波纹穿孔板夹角(板高与1/4板长对应的正切角)相同时, 在板长小于75 mm范围内波纹穿孔板有相似的声学性能。
- 波纹穿孔板 /
- 等效穿孔率 /
- 吸声特性 /
- 背腔深度
Abstract:
The dissipative effect of corrugated perforated plate on acoustic wave is studied in two cases of plane wave vertical incidence and grazing incidence in this paper. The results show that the acoustic performance of the corrugated perforated plate in both cases is different from that of the flat perforated plate. Under the condition of vertical incidence, the equivalent perforation rate can make the sound absorption coefficients of the corrugated perforated plate and the flat perforated plate coincide in the range of medium and low frequencies, but the corrugated perforated plate will have a double peak phenomenon that is different from the flat perforated plate at high frequencies. Further study reveals that it is due to the continuous change of the depth of the back cavity caused by the shape of the corrugated plate. Under the condition of grazing incidence, the corrugated perforated plate and flat perforated plate cannot be replaced by the equivalent perforation rate. The height and length of the corrugated perforated plate have obvious effects on its acoustic performance. When the angle of the corrugated plate is constant (the tangent angle corresponding to the plate height and a quarter of the plate length), the corrugated perforated plate with the plate length less than 75 mm has similar acoustic performance.
- Corrugated perforated plate /
- Equivalent perforation rate /
- Absorption characteristics /
- Back cavity depth

HTML全文

引言

对于现代航空发动机而言, 加力燃烧室的性能水平至关重要。自20世纪中期, 加力燃烧室在发动机中出现之后, 由于其封闭空间内高密度的热量释放, 在某些工况下会出现大幅度的燃烧振荡问题, 严重情况下, 会引起燃烧室内部部件的烧蚀损坏, 严重威胁着飞行的安全。此外, 近年来, 随着环境保护要求的日益提高, 燃气轮机的设计方面也对排放物的限制越来越严格。因此, 在燃烧室中一般采用贫油预混燃烧方式来降低氮氧化物的排放, 此种燃烧方式通常是在贫油熄灭的边界进行的, 然而燃油当量比的轻微扰动会引起较明显的非定常热释放, 这种非定常热释放有时会引起结构的严重破坏。因此, 如何抑制燃烧不稳定一直是急需解决的问题^[1-2]。

燃烧不稳定性是非定常热释放和声波充分耦合的结果。当火焰处的声波与非定常热释放的相位充分一致时, 就会使得非定常热释放的热能转化为声能, 当系统的耗散不足以消耗这些转化的声能时, 系统的声能不断积累, 压力振荡幅度不断提高, 最终在非线性机制下达到饱和, 表现为极限环的燃烧不稳定现象^[3]。

对于燃烧不稳定的控制方法分为有源控制方法和无源控制方法; 但现有有源控制方案技术上的可操作性不强, 难以真正投入实际应用。目前, 在工程中已得到成熟应用的还是无源控制方法, 比较典型的无源控制手段包括穿孔板^[4-5]、Helmholtz共鸣器^[6-8]、1/4波长和1/2波长管^[9]以及防振屏^[10]等。Helmholtz共鸣器被广泛应用于燃烧系统内, 主要针对低频的不稳定性模态。而穿孔板声衬往往对高频的燃烧不稳定性模态有较好的控制作用。但平板穿孔板往往只针对某一频率下的声波耗散作用明显, 而目前燃烧室中经常存在多个燃烧不稳定频率, 因此寻找对多个频率都有作用的控制方法至关重要。

在实际的发动机加力燃烧室中, 波纹穿孔板是常用的抑制燃烧振荡的方法。相比于平板穿孔板, 波纹穿孔板因其特殊的几何形状可以有效避免热应力集中, 同时还可以通过增加声散射的方式达到抑止燃烧不稳定性的效果。John等^[11]的发明专利中提到周向波纹穿孔板对燃烧不稳定性存在较好的抑制效果; Huang等^[12]通过有限元方法和实验方法对周期性波纹波导管进行了研究, 发现通过增加波导管的曲折性可以增加波导管的等效密度同时还可以提高多孔材料的低频吸声特性; Wang等^[13]基于建筑声学的需求, 研究了平面波在角度入射时大尺寸波纹穿孔板的吸声特性, 发现存在一定角度入射时的吸声效果优于垂直入射时的吸声效果。波纹穿孔板具有连续的曲率变化, 同时针对于不同声波入射方式和不同声模态入射时波纹穿孔板的吸声特性的细致研究目前还是比较欠缺的。而且, 随着加力燃烧室能量密度的提升, 加力燃烧室中声振荡的模态也变得越来越复杂, 因此, 细致研究波纹穿孔板对不同入射模态的吸声性能是非常有必要的。考虑到加力燃烧室中经常发生径向振荡和纵向振荡, 本文基于COMSOL软件^[14], 选取了两种不同的声波入射方式(垂直入射和掠入射)来探究波纹穿孔板的声学性能, 并尝试通过与平板穿孔板的对比, 来讨论波纹穿孔板的等价特性, 期望基于上述研究为工程设计提供一定的指导。

1. 理论模型

1.1 平面波垂直入射

根据研究需求, 在COMSOL软件二维压力声学物理接口中构建了如图1所示的平面波矩形管垂直入射模型。

图 1 平面波垂直入射模型

下载: 全尺寸图片幻灯片

该模型由完美匹配层、背景压力场、传播管段、穿孔板和背腔组成, 通过求解直角坐标系下二维波动方程^[15]得到管道内的声场。波动方程为

$\frac{{{\partial ^{\text{2}}}p}}{{\partial {{{x}}^2}}} + \frac{{{\partial ^{\text{2}}}p}}{{\partial {y^2}}} = \frac{1}{{{c_0}^2}}\frac{{{\partial ^{\text{2}}}p}}{{\partial {t^2}}},$

(1)

式中, $p$ 为声压, $t$ 为时间, 声速 ${c_{\text{0}}} = 340{\text{ m/s}}$ 。其中壁面边界均为硬壁面边界条件:

${({v_y})_{(y = 0,a)}} = 0,{\text{ }}{({v_x})_{(x = b)}} = 0,$

(2)

式中, ${v_x}$ , ${v_y}$ 分别为 ${{x, \, y}}$ 方向的速度分量。

完美匹配层选用笛卡尔多项式坐标拉伸类型, 长度为50 mm; 背景压力声场 ${p_i}$ 为平面波辐射, 沿 $x$ 方向入射, 其表达式为

${p_i} = {A_m}{{\text{e}}^{{\text{i}}wt}},$

(3)

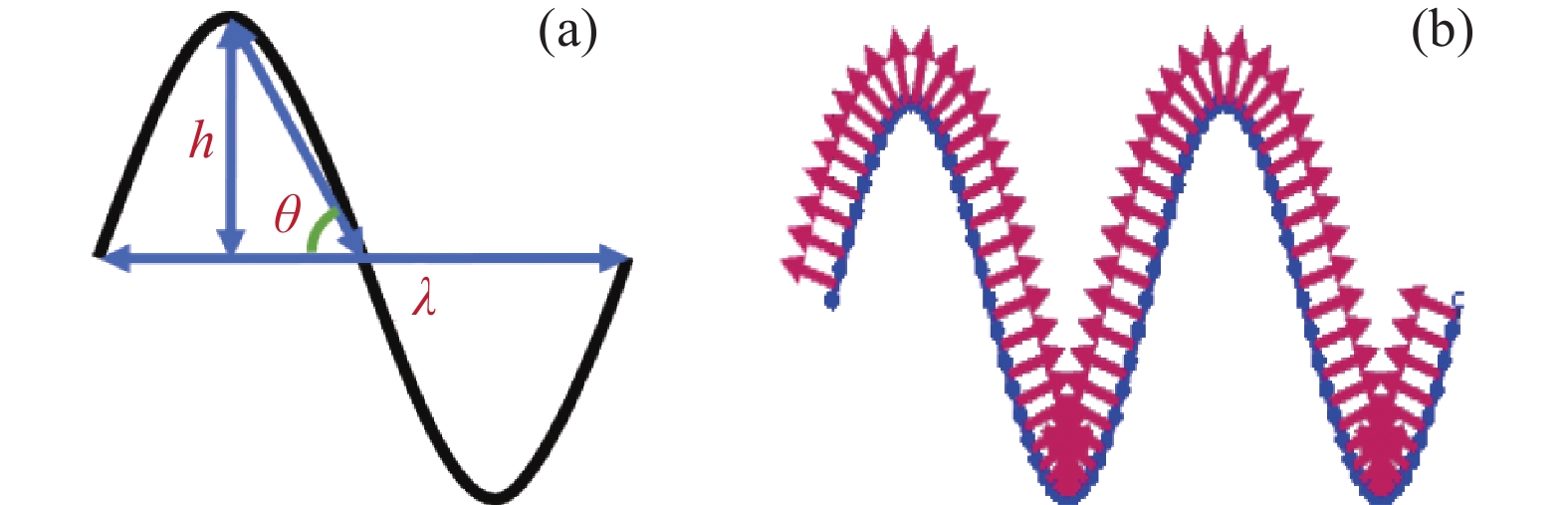
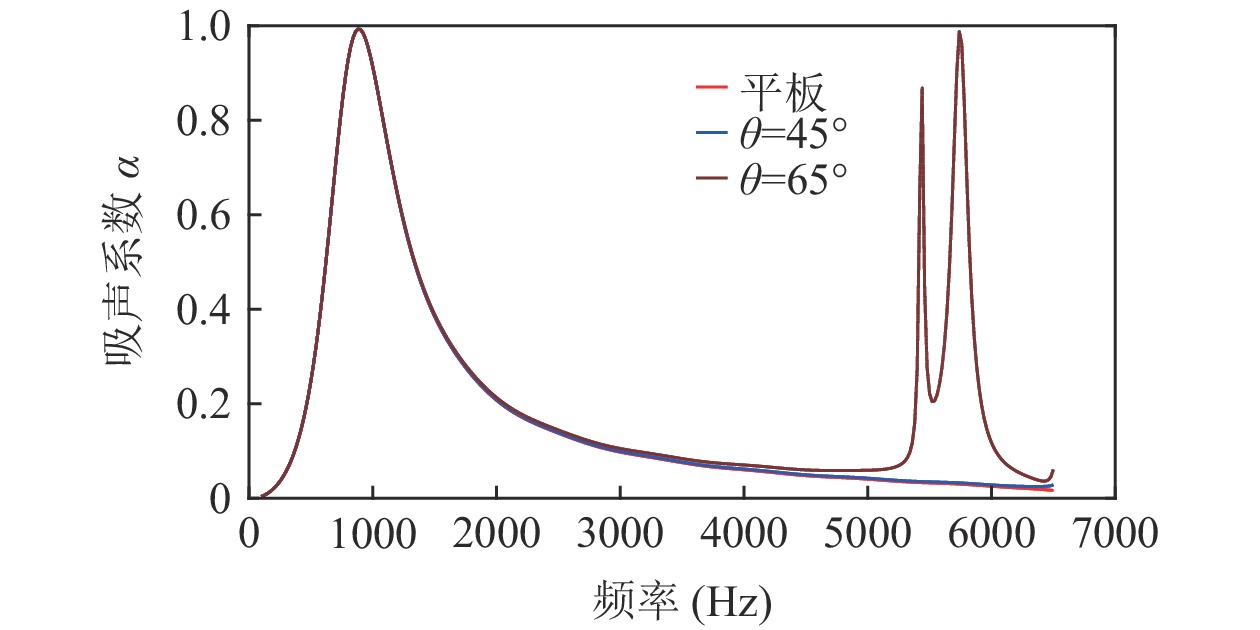
式中, 入射声压幅值 ${{{A}}_{{m}}}$ =1 Pa。

波纹穿孔板几何形状为正弦波形, 通过波长 $\lambda$ 和波高 ${{h}}$ 两个参数确定, 如图2(a)所示。在模型中波纹穿孔板由内部阻抗条件代替:

图 2 波纹穿孔板示意图 (a) 几何结构示意图; (b) 声阻抗示意图

下载: 全尺寸图片幻灯片

${Z_1} = \frac{p}{{{\rho _0}{c_0}{v}}},$

(4)

式中, ${Z_1}$ 为声阻抗, ${{v}}$ 为声质点速度, 空气密度 ${\rho _0} = 1.2\;{\rm kg} /{{\rm m}^3}$ 。

穿孔板阻抗设置如图2(b)所示, 阻抗大小选用无流动情况下的声阻抗模型^[16]:

$\begin{split}& {Z_{\text{1}}} = \frac{{{\rm i}{k_0}t}}{{1 - {{\varLambda }}({k_\nu }d/2)}}\frac{1}{\sigma } + \frac{{2\sqrt {2\omega \nu } }}{{\sigma {c_0}}} + (1 - 0.7\sqrt \sigma )\frac{{0.85{\rm i}{k_0}d}}{{2\sigma }}, \\& {k_\nu } = \sqrt { - {\rm i}\omega /\nu } ,\;\; {{\varLambda }}(x) = \frac{{2{\rm{J}_1}(x)}}{{x{\rm{J}_0}(x)}}, \\[-12pt] \end{split}$

(5)

式中, ${k_0} = \omega /{c_0}$ , 声速 ${c_0}$ =340 ${{\rm{m}}} /{\rm{s}}$ , 动力黏性系数 $\nu = 1.511 \times {10^{ - 5}}\;{{{\rm{m}}} ^2}/{\rm{s}}$ , $\sigma$ , ${{t}}$ , ${{d}}$ 分别为穿孔板的穿孔率、板厚和孔径, ${\text{J(}} \cdot {\text{)}}$ 表示贝塞尔函数。

传播管段长度 $L$ 为300 mm, 管道宽度 ${{a}}$ 为25 mm, 由二维矩形管截止频率计算公式:

${f_{{n_y}}} = \frac{{{c_0}}}{2} \cdot \frac{m}{{{l_y}}},$

(6)

其中, ${l_y}$ 为管宽, $m$ 为 $y$ 方向的模态数, 可得到该模型一阶截止频率为6923 Hz。

本模型计算频率范围为100 ~ 6500 Hz, 步长为20 Hz。采用自由三角形网格, 最大尺寸为最小波长的1/50。

1.2 平面波掠入射

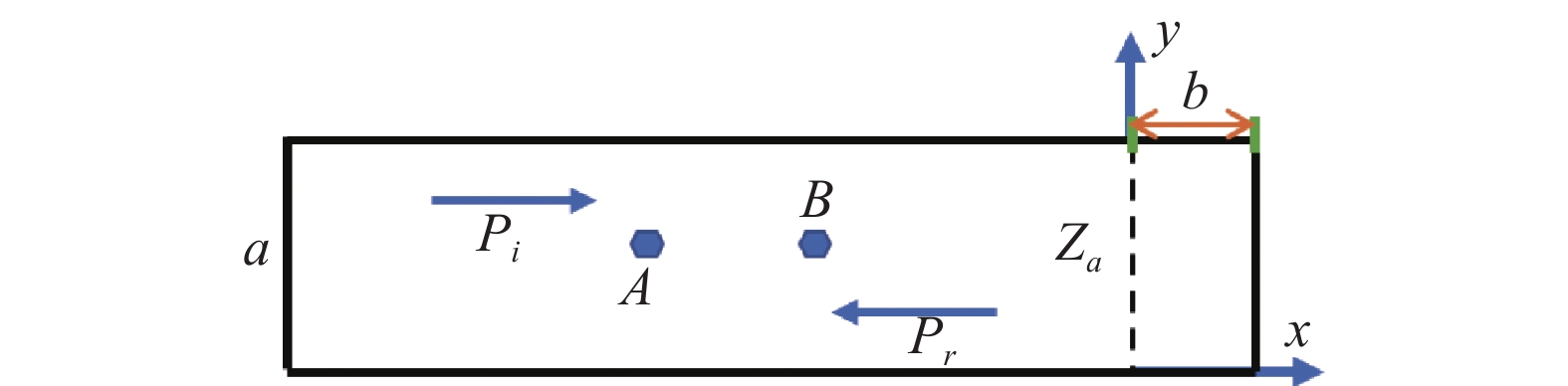
根据研究需求, 在COMSOL软件二维轴对称线性势流物理接口中构建了如图3所示的平面波圆管掠入射模型。

图 3 平面波掠入射模型

下载: 全尺寸图片幻灯片

该模型由入口完美匹配层、声衬前段、声衬段、声衬后段和出口完美匹配层组成, 通过势流波动方程对管道内的声场进行求解:

$\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial \phi }{\partial r}\right) + \frac{1}{{r}^{2}}\frac{{\partial }^{2}\phi }{\partial {\theta }^{2}} + \frac{{\partial }^{2}\phi }{\partial {\textit{z}}^{2}}=\frac{1}{{c}_{0}{}^{2}}\frac{{\partial }^{\text{2}}\phi }{\partial {t}^{2}}\text{, } \; \phi ={\displaystyle \int { \dfrac{p}{{\rho }_{0}}}}\rm{d}t\text{, }$

(7)

式中, $\phi$ 为速度势。

其中, 管道半径 $R = 100{\text{ }}{\rm{mm}}$ , 除声衬段外壁面边界均为硬壁面边界条件。完美匹配层选用笛卡尔多项式坐标拉伸类型, 长度为2倍管道直径400 mm; 截面O为平面波入射截面, 幅值为1 Pa; 声衬前端和后段长度均为3倍管道直径600 mm; 声衬段长度为 $L = 300\;{{\rm{mm}}}$ , 穿孔板同样由内部阻抗条件代替, 阻抗方向沿穿孔板法向方向, 阻抗大小选用同1.1节相同的阻抗模型; 通过圆管一阶截止频率计算公式得到该模型的一阶截止频率为1014.2 Hz:

${f}_{c}={f}_{10}={k}_{10}\frac{{c}_{0}}{2\pi }=1.84\frac{{c}_{0}}{2\pi R}\text{, }$

(8)

式中, $R$ 为管道半径, 声速 ${c_0}$ =340 m/s。

本模型计算频率范围100 ~ 3000 Hz, 步长10 Hz, 采用自由三角形网格, 最大尺寸为最小波长的1/20。

2. 模型验证

2.1 平面波垂直入射

为了验证平面波垂直入射时模型的有效性, 对比了穿孔板为平板时末端声衬吸声系数的解析解与数值解。此时模型变为如图4所示的情形。

图 4 声波垂直入射示意图

下载: 全尺寸图片幻灯片

根据声阻抗率的定义计算声衬的吸声系数 $\alpha$ 的解析解^[15]:

${\textit{z}}_{a}=\frac{p}{v}=\left(\frac{1 + \left|{r}_{p}\right|{{\rm{e}}}^{{\rm{i}}\sigma \pi }}{1-\left|{r}_{p}\right|{{\rm{e}}}^{{\rm{i}}\sigma \pi }}\right){\rho }_{0}{c}_{0},$

$\left|{r}_{p}\right|{{\rm{e}}}^{{\rm{i}}\sigma \pi }=\frac{\dfrac{{\textit z}_{a}}{{\rho }_{0}{c}_{0}}-1}{\dfrac{{\textit z}_{a}}{{\rho }_{0}{c}_{0}} + 1}\text{, } \;\; \alpha = 1 - {\left| {{r_p}} \right|^2}.$

(9)

末端声衬的声阻抗率 ${{\textit{z}}_a} = ({{\textit{z}}_1} + {{\textit{z}}_2}){\rho _0}{c_0}$ , ${{\textit{z}}_1}$ 为穿孔板相对声阻抗率, 如式(5)所示, ${{\textit{z}}_2}$ 为背腔相对声阻抗率:

${{\textit{z}}_2} = - {\rm{i}}\cot ({k_0}b),$

(10)

式中, ${\rm{i}} = \sqrt { - 1}$ , ${k_0} = \omega /{c_0}$ , b为背腔深度。

在COMSOL中为了得到声衬吸声系数的数值解, 采用双传声器法来计算, 声压反射系数 ${r_p}$ 为

${r_p} = \frac{{{p_{ar}}}}{{{p_{ai}}}} = \left| {{r_p}} \right|{{\rm{e}}^{{\rm{i}}\sigma \pi }} = \frac{{{p_A}{{\rm{e}}^{ - {\rm{i}}{k_0}{x_2}}} - {p_B}{{\rm{e}}^{ - {\rm{i}}{k_0}{x_1}}}}}{{{{\rm{e}}^{{\rm{i}}k_0({x_1} - {x_2})}} - {\rm{e}^{\rm{i}k_0({x_2} - {x_1})}}}}/\frac{{{p_A}{{\rm{e}}^{{\rm{i}}{k_0}{x_2}}} - {p_B}{{\rm{e}}^{{\rm{i}}{k_0}{x_1}}}}}{{{{\rm{e}}^{{\rm{i}}k_0({x_2} - {x_1})}} - {{\rm{e}}^{{\rm{i}}k_0({x_1} - {x_2})}}}},$

(11)

式中, ${p_A}$ , ${p_B}$ 分别为测点A, B处的声压, ${x_1}$ , ${x_2}$ 分别为测点A, B的位置。再由式(9)便可得到吸声系数。

根据GB/T 18696.2-2002阻抗管中吸声系数和声阻抗的测量^[17]的要求, 两个传声器之间的间距s (m)应满足:

${f_u} \cdot s < 0.45{c_0},$

(12)

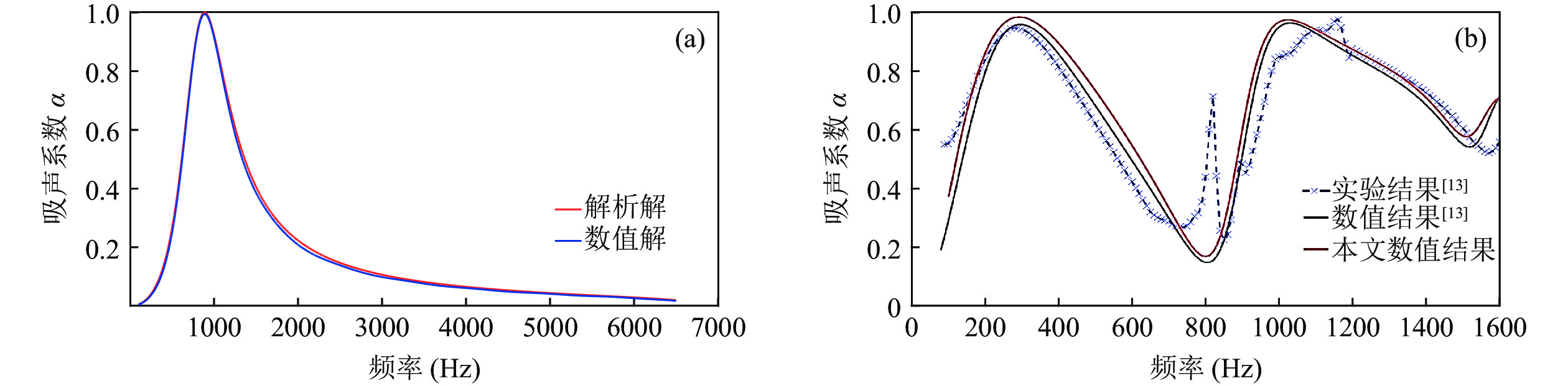
式中, ${f_u}$ 为阻抗管工作频率上限, ${f_u}$ 根据避免出现非平面波简正波模式的原则选取, 且传声器间距应大于感兴趣的低频相应的波长的5%, 对于1000 Hz此值为17.3 mm, 本模型中两测点间距为20 mm, ${x_1}$ = −220 mm, ${x_2}$ = −200 mm, y坐标均为12.5 mm。

模型对比了如下声衬的解析解与数值解, 其中计算参数如表1所示, 如无特殊说明, 后文讨论垂直入射时, 孔板参数及腔深均采用表1中给出的数值。解析解与数值解的计算结果如图5(a)所示; 与香港大学Wang等^[13]的实验结果和三维有限元计算结果进行对比, 结果如图5(b)所示。

表 1 平板声衬结构参数

穿孔率 σ	板厚 t (mm)	孔径 d (mm)	背腔深度 b (mm)
1%	1	0.5	25

下载: 导出CSV

| 显示表格

从图5(a)中可以看出, 平板穿孔板时COMSOL数值模拟结果与解析解的计算结果符合较好; 图5(b)也显示了本文二维COMSOL数值模拟结果与实验结果、三维有限元计算结果较好的一致性, 从而验证了本模型的有效性。

图 5 平面波垂直入射时末端声衬的吸声系数 (a) 平板穿孔板声衬; (b) 波纹穿孔板声衬

下载: 全尺寸图片幻灯片

2.2 平面波掠入射

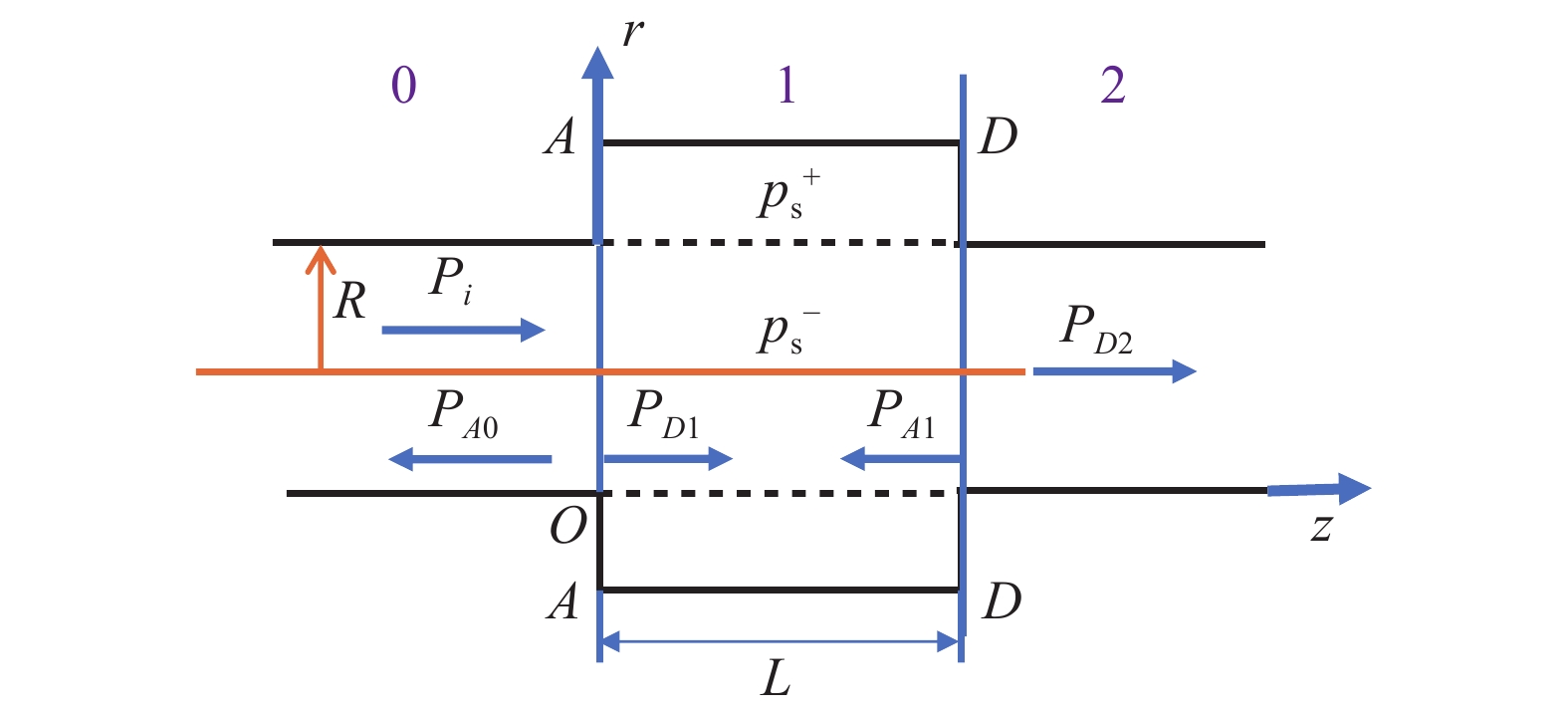
为了验证平面波掠入射时模型的有效性, 同样将波纹穿孔板退化为平板穿孔板, 此时模型变为如图6所示的情形。

图 6 声波掠入射示意图

下载: 全尺寸图片幻灯片

声波掠入射情况下可以通过传递损失TL和吸声系数 $\alpha$ 来评价声衬的声学特性。传递损失定义为声衬上游 ${\textit{z}} = {{\textit{z}}_u}$ 处管道截面声能量流与声衬下游 ${\textit{z}} = {{\textit{z}}_d}$ 处管道截面声能量流之比的声能量级表示形式:

${\rm{TL}} = 10\lg \left( {\frac{{W({{\textit{z}}_u})}}{{W({{\textit{z}}_d})}}} \right).$

(13)

吸声系数定义为经过声衬辐射出的声能量与进入声衬的入射声能量之比。模型中假设管道是无限长的, 即声衬下游截面不存在往上游传播的声波。

$\alpha = 1 - \frac{{{W_r}({{\textit{z}}_u}) + {W_i}({{\textit{z}}_d})}}{{{W_i}({{\textit{z}}_u})}},$

(14)

式中, ${W_i}\left( {{{\textit{z}}_u}} \right)$ 为入射声能量, ${W_r}\left( {{{\textit{z}}_u}} \right)$ 为声衬前截面反射声能量, ${W_i}\left( {{{\textit{z}}_d}} \right)$ 为声衬后截面透射声能量。

文献[18]给出了平面波掠入射条件下非局域声衬的解析解, 该研究通过传递单元法对声场进行求解, 其中散射声场可通过等价分布源方法^[19]及阻抗边界条件求得, 再借助无流动或等截面时的界面匹配条件, 整个声场就可得到求解。

为了得到声衬的吸声系数和传递损失的数值解, 数值模拟中, 选取声衬前声能量计算截面A和声衬后声能量计算截面D, 两者距离声衬段的距离均为两倍管道直径0.4 m。根据Morfey^[20]提出的理论, 无流动的管道中轴向声强 $I$ 可以表示为

$I(x,y,{\textit{z}}) = \dfrac{1}{2}{{\rm{Re}}} (p{u^ * }),$

(15)

式中, “*”表示共轭, Re表示实部。则声能量流为

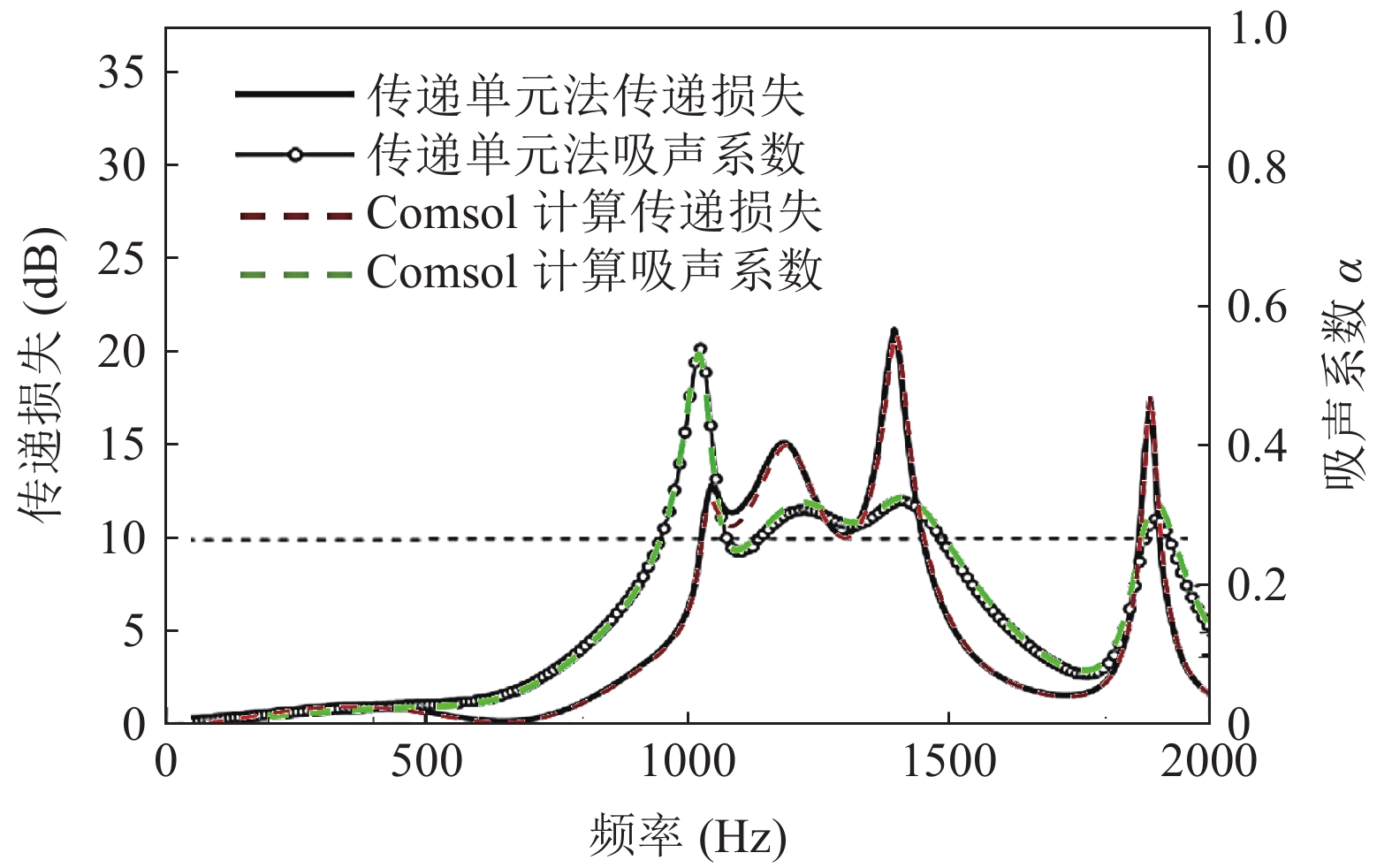
$W({\textit{z}}) = \int\limits_s {I(x,y,z){\rm d}s} = \int\limits_s {\dfrac{1}{2}{{\rm{Re}}} (p{u^*}){\rm{d}}s} .$

(16)

与文献[18]中穿孔板为平板时的结果进行比较, 声衬段结构参数如表2所示。解析解与数值解的计算结果如图7所示, 可以看出, COMSOL数值模拟结果与解析解^[18]的计算结果符合较好, 验证了本模型的有效性。

表 2 声衬段结构参数

管径 R (mm)	声衬段长度 L (mm)	穿孔率 σ	板厚 t (mm)	孔径 d (mm)	背腔深度 b (mm)
100	300	2%	0.87	1.83	25

下载: 导出CSV

| 显示表格

图 7 平面波掠入射时壁面平板声衬的传递损失和吸声系数

下载: 全尺寸图片幻灯片

3. 结果分析

3.1 平面波垂直入射

3.1.1 夹角θ的影响

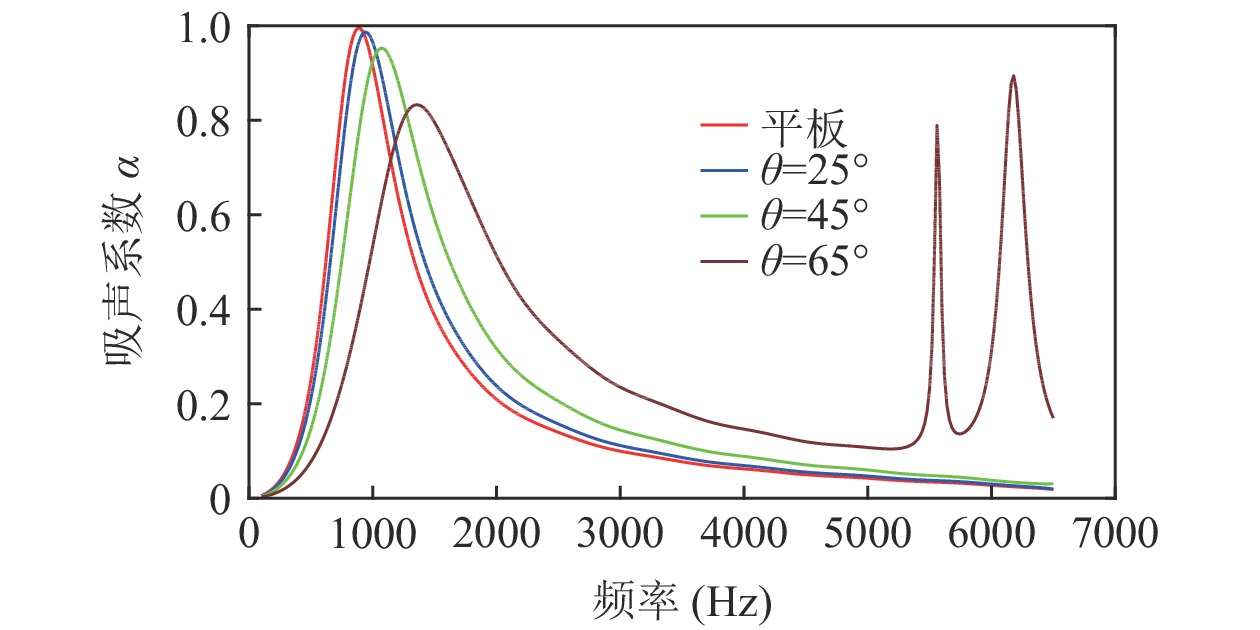
本文主要研究在矩形管内波纹穿孔板形状对其声学性能的影响, 研究发现在低频时夹角 $\theta$ ( $\tan \theta = 4h/\lambda$ )对波纹穿孔板的吸声特性有着较大的影响, 当该参数不变即波高h与波长 $\lambda$ 的比值一定时, 吸声系数在低频段相同, 如图8所示。穿孔板参数如表1所示, 此处穿孔率 $\sigma$ 为孔的面积与波纹板面积的比值。 $\theta$ 一定时, 波高h与波长 $\lambda$ 的大小见表3, 此处波长 $\lambda$ 与管宽同宽, 即管道内波纹板只有一个完整周期, 由式(6)可知, 当管道宽度变小时, 矩形管的一阶截止频率随之增大, 所以平面波假设依旧成立。

图 8 夹角θ相同时的吸声系数 (a) 夹角θ = 10°; (b) 夹角θ = 30°; (c) 夹角θ = 50°

下载: 全尺寸图片幻灯片

表 3 波纹穿孔板几何参数

	板长 λ (mm)	12.5	15	20	25
板高 h (mm)	θ = 0°	0.55	0.66	0.88	1.10
	θ = 30°	1.80	2.17	2.89	3.61
	θ = 50°	3.72	4.47	5.96	7.45

下载: 导出CSV

| 显示表格

从图8中可以看出, 当夹角θ相同时, 在低频段能够较好地重合, 但在高频时差别较大; 同时, 当波纹穿孔板夹角较大时, 波纹穿孔板声衬的吸声系数与平板时存在较大差异, 但当夹角较小时, 波纹穿孔板声衬的吸声系数与平板时几乎没有区别。

图9显示了当固定波长 $\lambda = 12.5$ mm (即波纹板存在两个完整波形), 通过改变板高h来改变夹角θ时声衬吸声系数的变化, 从图中可以看出波纹穿孔板的最大吸声系数随夹角θ的增大而减小, 且频率向高频移动, 当夹角θ = 65°时高频时会出现双尖锋现象。

图 9 不同夹角θ时的吸声系数

下载: 全尺寸图片幻灯片

3.1.2 等效穿孔率与背腔

针对夹角相同时, 吸声系数在低频时重合的现象, 引入等效穿孔率的概念^[14]:

$\sigma ' = \frac{{{L_A}}}{{{L_D}}}\sigma ,$

(17)

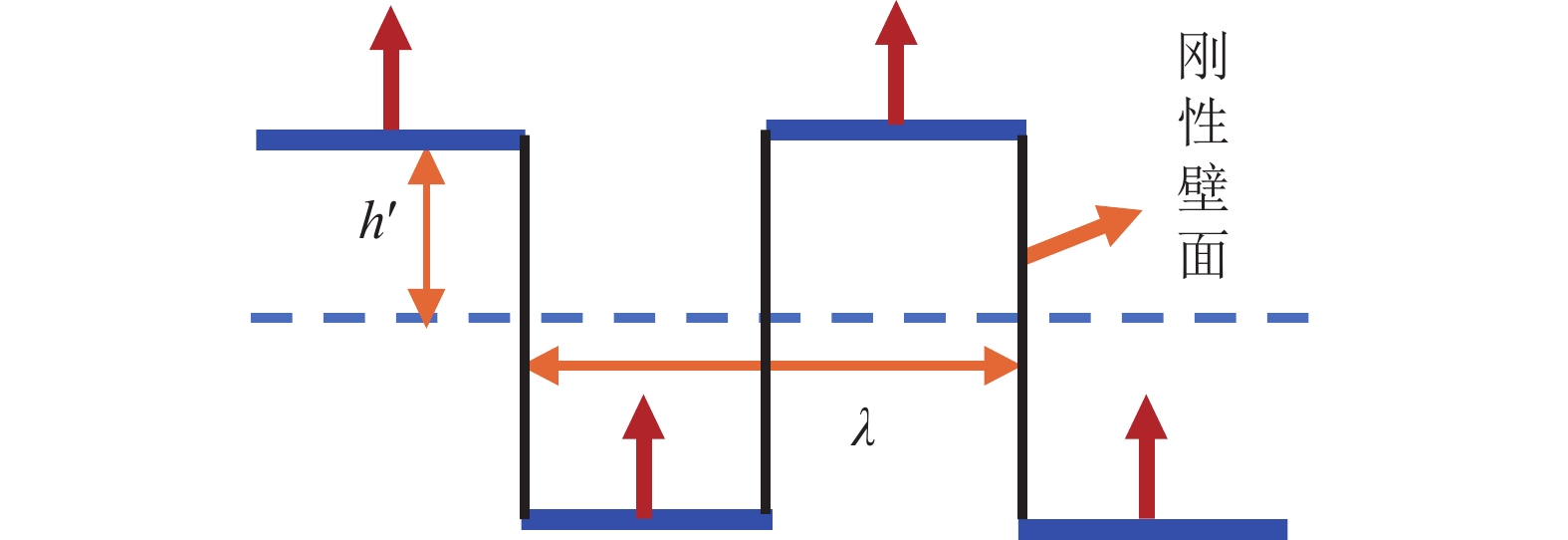
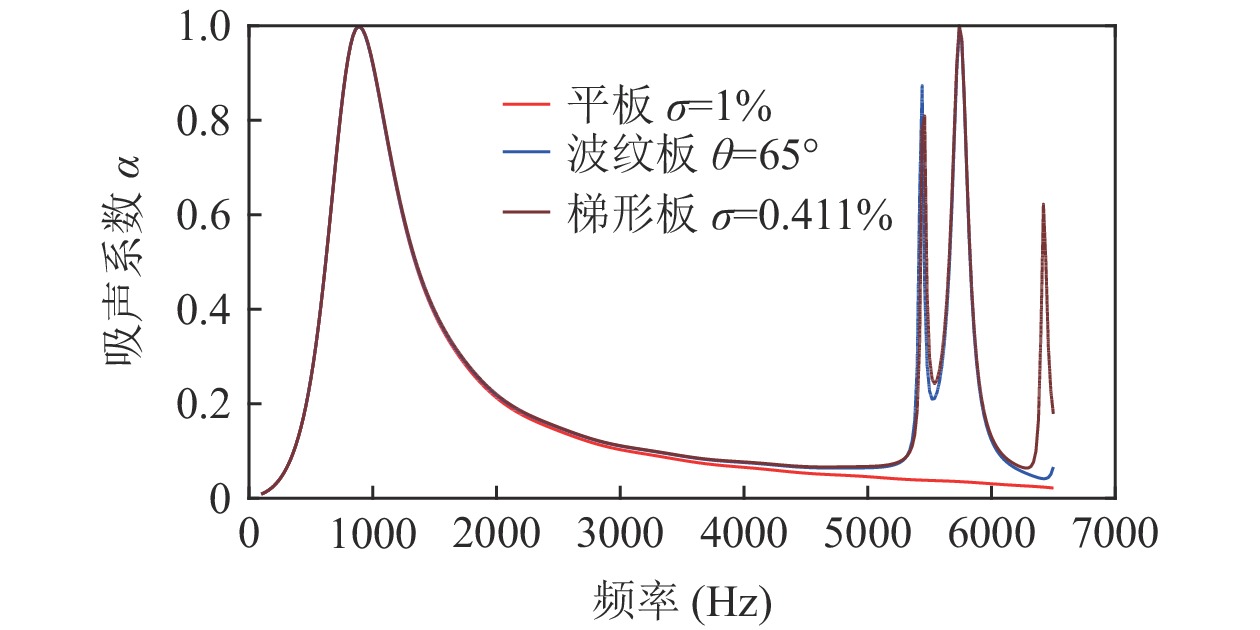
其中, $\sigma '$ 为波纹板等效穿孔率, $\sigma$ 为波纹板实际穿孔率, ${L_A}$ 为波纹板面积, ${L_D}$ 为波纹板垂直投影面积。为便于研究, 设定等效穿孔率 $\sigma ' = 1\%$ , 计算波长 $\lambda = 12.5$ mm时夹角θ = 45°和θ = 65°所对应的实际穿孔率, 分别为0.684%和0.411%, 其吸声系数如图10所示, 可以看出, 低频时波纹板声衬的吸声系数能很好地与等效穿孔率条件下的平板声衬的吸声系数重合, 但高频时, 夹角θ = 65°情况下曲线无法重合。故平面波垂直入射时波纹穿孔板的低频吸声特性可用等效穿孔率来解释。

图 10 波纹板等效穿孔率后的吸声系数

下载: 全尺寸图片幻灯片

对于夹角较大时出现的双尖锋现象, 本文通过梯形板侧面验证了波纹板导致的背腔变化是双尖峰产生的原因。图2(b)的波纹板简化为如图11所示的梯形板, 其中 ${{h'}}$ 为梯形板的板高, $\lambda$ 为梯形板一个周期的长度, 与波纹板相同; 红色箭头表示声阻抗的方向, 其穿孔率为等效穿孔率, 其他参数与波纹穿孔板相同, 黑色壁面则为刚性壁面。

图 11 梯形板结构图

下载: 全尺寸图片幻灯片

图12对比了 $\lambda$ = 12.5 mm, ${{h'}}$ = 4.74 mm (此处 $h'{\text{ = }}\sqrt 2 h/2$ , $h$ 为θ = 65°时波纹板板高, 但这一比值并不存在普遍规律), $\sigma ' = 0.411\text{%}$ 时梯形穿孔板与图9中θ = 65°时波纹穿孔板的吸声系数。从图中可以清楚地看出梯形板和波纹板的吸声系数不仅在低频时能够重合, 而且高频时的双峰也能够重合, 但是其后的峰值并未重合, 说明波纹板的吸声系数在高频处的双峰现象是由其腔深的连续变化而引起的。

图 12 梯形板与波纹板吸声系数对比

下载: 全尺寸图片幻灯片

3.2 平面波掠入射

在波纹穿孔板实际工作环境中, 声波并非只有垂直入射情况, 还可能包含掠入射甚至是斜入射情况。本节重点讨论声波掠入射时, 波纹穿孔板的吸声特性。同样通过改变波纹板的形状来研究其引起的变化, 同时由于非局域反应声衬在掠入射时的声学性能与其轴向长度有关^[21], 本研究中固定声衬段的长度 $L = 300{\text{ }}{{\rm{mm}}}$ , 通过改变声衬段中波纹的完整周期数来调整波纹板的长度 $\lambda$ 。

3.2.1 夹角θ的影响

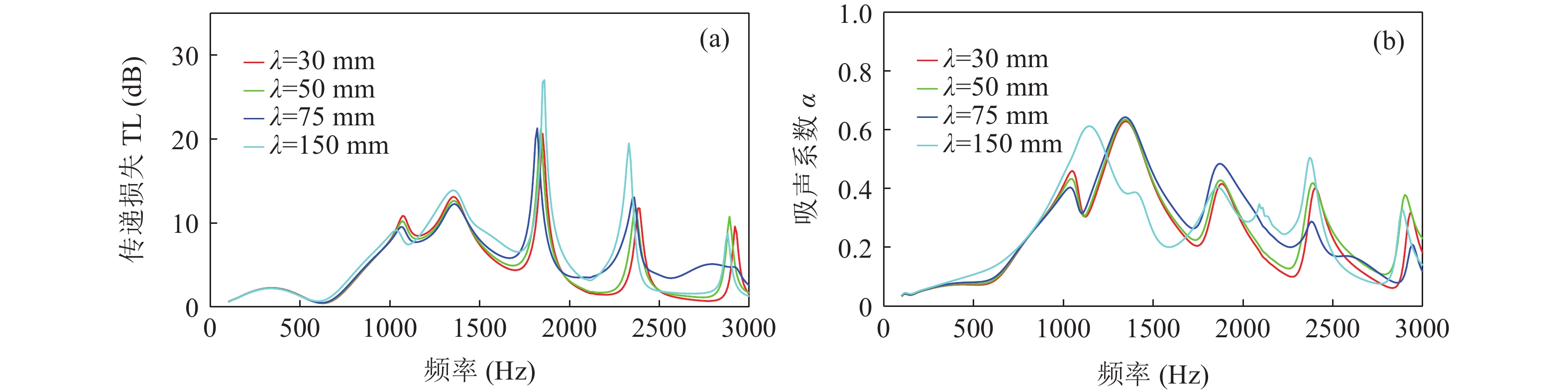
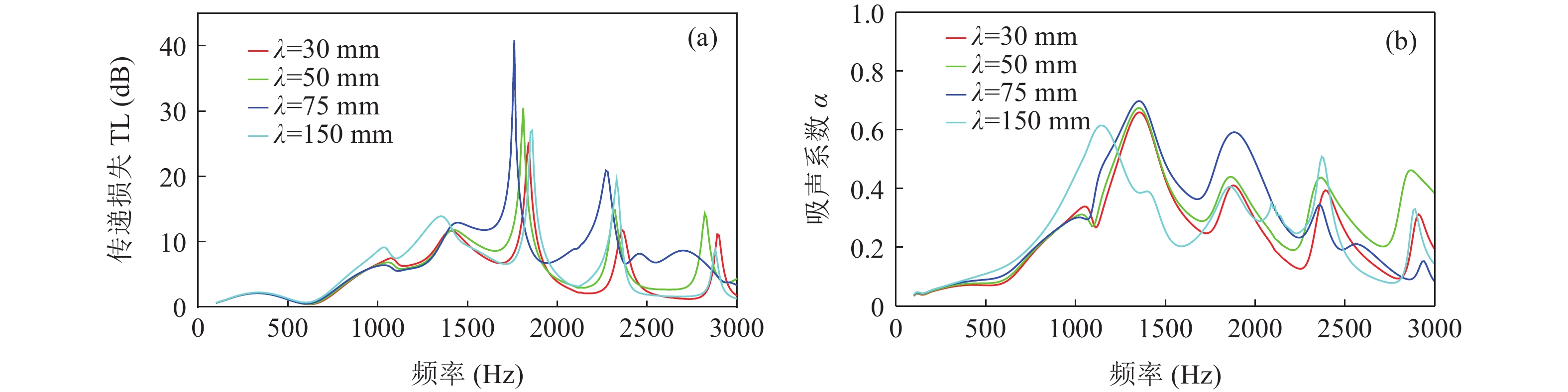
首先研究掠入射时夹角 $\theta$ 对波纹穿孔板吸声特性的影响, 分别选取夹角 $\theta$ =25°, $\theta$ = 35°两种情况, 穿孔板参数为: 穿孔率 $\sigma$ = 2%, 板厚 $t = 1$ mm, 孔径 $d = 1$ mm, 背腔深度 $b = 25$ mm, 板高h和板宽 $\lambda$ 见表4。 $\theta$ = 25°, 35°时不同波长波纹板的传递损失和吸声系数分别如图13和图14所示。

表 4 波纹穿孔板几何参数

	板长 λ (mm)	30	50	75	150
板高 h (mm)	θ = 25°	3.50	5.83	8.74	17.50
板高 h (mm)	θ = 35°	5.25	8.75	13.13	26.26

下载: 导出CSV

| 显示表格

图 13 夹角θ=25°时波纹穿孔板的声学特性 (a) 传递损失; (b) 吸声系数

下载: 全尺寸图片幻灯片

图 14 夹角θ=35°时波纹穿孔板的声学特性 (a) 传递损失; (b) 吸声系数

下载: 全尺寸图片幻灯片

从图中可以看出, 夹角 $\theta$ 相同时, 波纹板有相似的变化趋势, 在板高较小且低频时能够完全重合; 当板高过大时, 差异变得明显。因此, 平面波掠入射时波纹板形状并不能由夹角 $\theta$ 单独来表征, 这与垂直入射时差异较大。

3.2.2 板高h和板长λ的影响

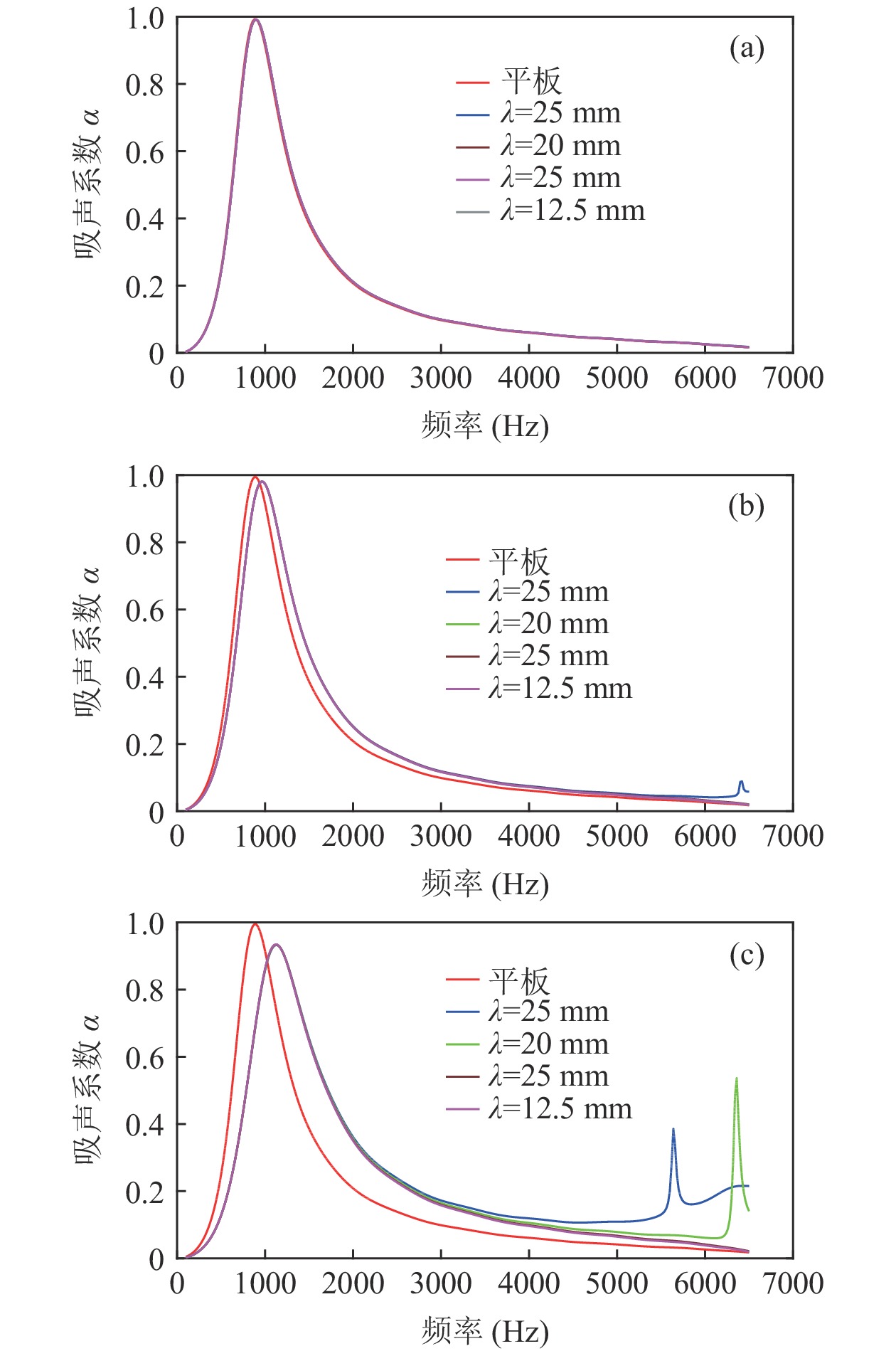
为了进一步分析波纹板几何因素的影响, 首先研究了波纹板高度 $h$ 的影响, 选定波纹板长度 $\lambda = 300$ mm, 即声衬段只存在一个完整波纹。分别选取 $h = 5{\text{ mm}}$ , 15 mm, 25 mm, 35 mm (波纹板夹角 $\theta \leqslant$ 25°), 波纹板其他参数与3.2.1节相同。

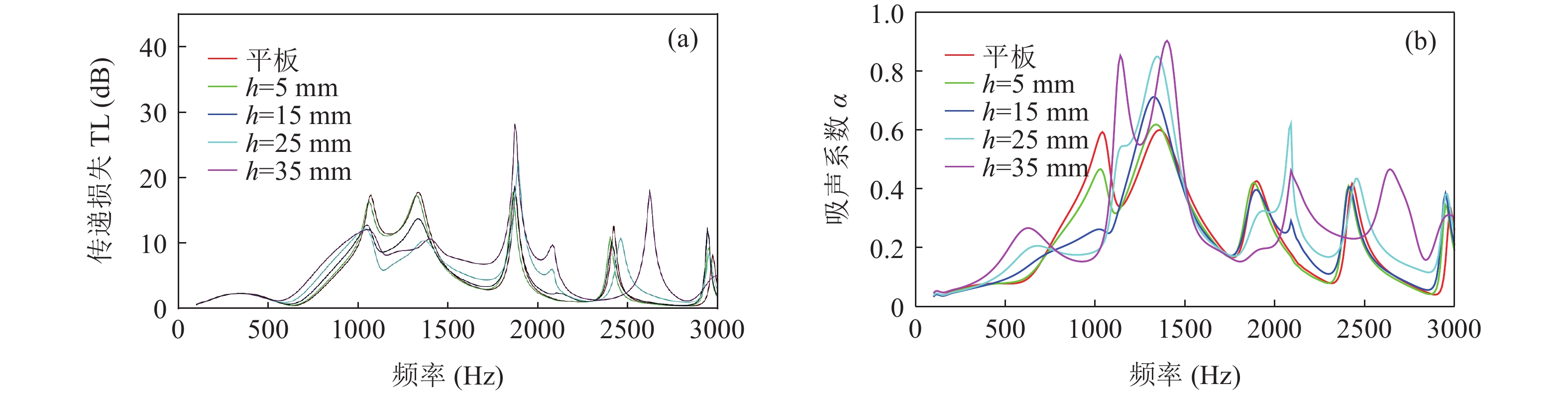
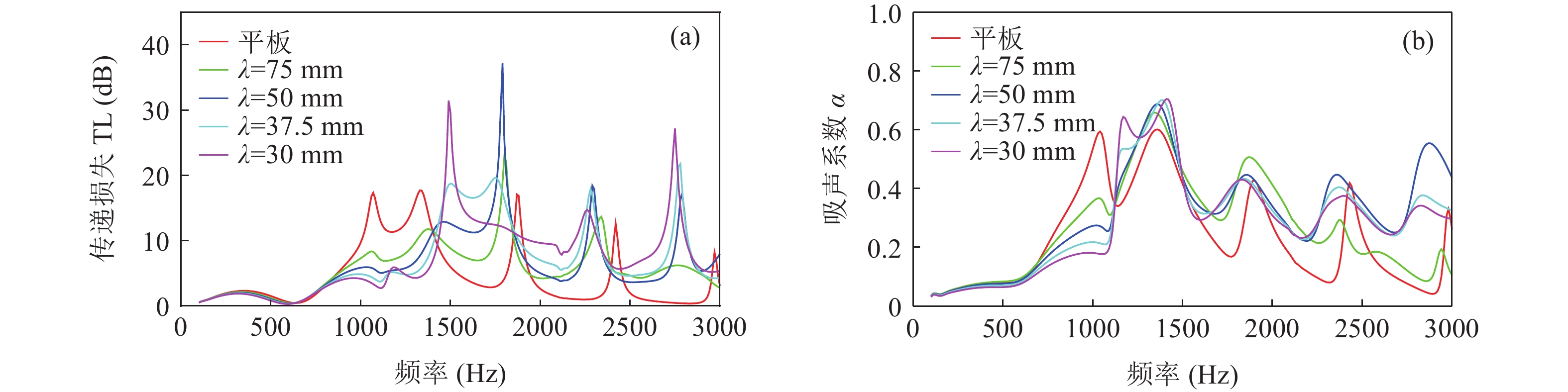
从图15中可以看出, 波纹穿孔板与平板穿孔板的声学性能存在较大差异。传递损失在 $0\sim 500{\text{ Hz}}$ 内与平板穿孔无异; 在 $500\sim1000{\text{ Hz}}$ 内优于平板穿孔板且随板高增大而逐渐增大; 在 $1000\sim1500{\text{ Hz}}$ 内变化较为复杂, 呈现出随板高先减小后增大的趋势; 在 $2000{\text{ Hz}}$ 左右随板高增加会出现一个新的尖峰, 且在 $2500{\text{ Hz}}$ 左右尖峰频率随板高增加往高频移动。对于吸声系数, 在 $500{\text{ Hz}}$ 之前已表现出与平板穿孔板的差异, 并不同于传递损失所呈现的规律; 在 $750{\text{ Hz}}$ 左右吸声系数随板高的变化规律与传递损失相反; 吸声系数双峰的频率随板高增大逐渐向高频移动, 且随板高的增加表现出更加优异的吸声效果。为了进一步研究板长 $\lambda$ 的影响, 固定板高 $h = 10{\text{ mm}}$ , 改变板长 $\lambda = 75{\text{ mm}}$ , 50 mm, 37.5 mm, 30 mm (只选择了特征明显的参数), 结果如图16所示。

图 15 不同板高时波纹穿孔板声学特性 (a) 传递损失; (b) 吸声系数

下载: 全尺寸图片幻灯片

图 16 不同板长时波纹穿孔板声学特性 (a) 传递损失; (b) 吸声系数

下载: 全尺寸图片幻灯片

从图中可以看出, 波纹穿孔板的传递损失在 $0\sim800{\text{ Hz}}$ 内与平板相同, 波纹穿孔板在平板双峰位置的传递损失随波长变短逐渐降低, 但波纹穿孔板的双峰移到了 $1500\sim2000{\text{ Hz}}$ 之间并随波长缩短出现了双峰的左右尖峰交替占优的情况。对于吸声系数, 同样在低频时与平板穿孔板没有差异, 双尖峰也向高频移动, 且在更高频率波纹穿孔板的吸声系数要优于平板穿孔板。

3.2.3 等效参数研究

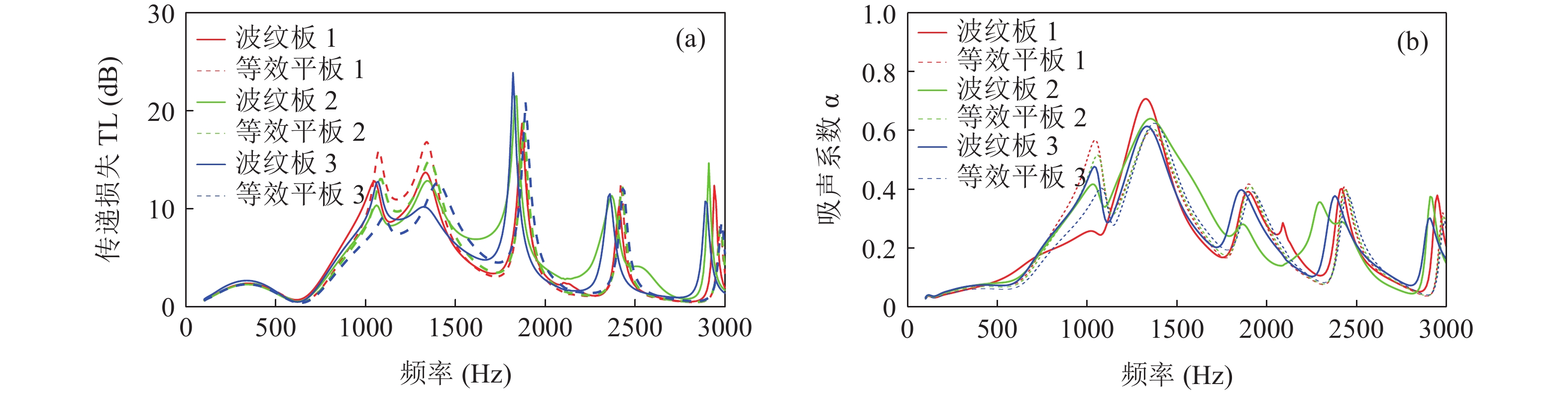
基于平面波垂直入射时的研究经验, 同样研究等效穿孔率的影响。随机选取了3组算例进行验证, 此处固定波纹穿孔板的穿孔率 $\sigma$ = 2%, 计算其对应的等效穿孔率 $\sigma '$ , 对比波纹穿孔板与等效穿孔率条件下的平板穿孔板的区别, 验证参数见表5, 结果如图17所示。

表 5 等效穿孔率验证参数

波纹板序号	波纹板板长 λ (mm)	波纹板板高 h (mm)	波纹板穿孔率 σ (%)	等效穿孔率 σ' (%)
波纹板 1	300	15	2	2.05
波纹板 2	100	10	2	2.18
波纹板 3	30	5	2	2.47

下载: 导出CSV

| 显示表格

图 17 等效穿孔率对比 (a) 传递损失; (b) 吸声系数

下载: 全尺寸图片幻灯片

从图17中可以看出, 等效穿孔率后的平板穿孔板与波纹穿孔板的声学性能存在较大差异, 因此在掠入射条件下, 波纹穿孔板的吸声变化无法用等效穿孔率解释。

从上述对掠入射声波的研究中不难发现, 声波入射方向对波纹穿孔板的吸声特性有较大影响, 同时, 对于掠入射情况, 波纹板很难等效成平板的参数进行对比研究, 可见, 这种穿孔板在实际应用中的效果需要精心设计。

4. 结论

基于COMSOL软件, 通过数值模拟的方法对平面波垂直入射和掠入射条件下波纹穿孔板的声学特性进行了研究, 主要结论如下:

(1) 在平面波垂直入射情况下, 波纹穿孔板相对于平板穿孔板吸声系数的主峰所对应的频率有所偏移, 通过等效穿孔率替换, 发现在其他条件相同的情况下, 波纹穿孔板吸声系数的主峰可以与等效穿孔率条件下的平板穿孔板的吸声系数相重合。但在高频范围内, 波纹穿孔板吸声系数会出现异于平板穿孔板的双尖锋现象。通过梯形板改变背腔深度, 发现此现象是由穿孔板波纹形状引起的背腔深度连续变化所导致的, 并可以通过梯形板简化来近似地描述波纹穿孔板的声学特性。

(2) 在平面波掠入射条件下, 波纹穿孔板的传递损失和吸声系数同样与平板穿孔板存在差异, 但并不存在类似于垂直入射条件下的等效参数。改变波纹穿孔板的板高和板长对波纹穿孔板的声学性能有明显的影响。当波纹穿孔板夹角 $\theta$ 相同时, 在板长小于75 mm范围内波纹穿孔板的声学特性近似。

图 1 平面波垂直入射模型

下载: 全尺寸图片幻灯片

图 2 波纹穿孔板示意图 (a) 几何结构示意图; (b) 声阻抗示意图

下载: 全尺寸图片幻灯片

图 3 平面波掠入射模型

下载: 全尺寸图片幻灯片

图 4 声波垂直入射示意图

下载: 全尺寸图片幻灯片

图 5 平面波垂直入射时末端声衬的吸声系数 (a) 平板穿孔板声衬; (b) 波纹穿孔板声衬

下载: 全尺寸图片幻灯片

图 6 声波掠入射示意图

下载: 全尺寸图片幻灯片

图 7 平面波掠入射时壁面平板声衬的传递损失和吸声系数

下载: 全尺寸图片幻灯片

图 8 夹角θ相同时的吸声系数 (a) 夹角θ = 10°; (b) 夹角θ = 30°; (c) 夹角θ = 50°

下载: 全尺寸图片幻灯片

图 9 不同夹角θ时的吸声系数

下载: 全尺寸图片幻灯片

图 10 波纹板等效穿孔率后的吸声系数

下载: 全尺寸图片幻灯片

图 11 梯形板结构图

下载: 全尺寸图片幻灯片

图 12 梯形板与波纹板吸声系数对比

下载: 全尺寸图片幻灯片

图 13 夹角θ=25°时波纹穿孔板的声学特性 (a) 传递损失; (b) 吸声系数

下载: 全尺寸图片幻灯片

图 14 夹角θ=35°时波纹穿孔板的声学特性 (a) 传递损失; (b) 吸声系数

下载: 全尺寸图片幻灯片

图 15 不同板高时波纹穿孔板声学特性 (a) 传递损失; (b) 吸声系数

下载: 全尺寸图片幻灯片

图 16 不同板长时波纹穿孔板声学特性 (a) 传递损失; (b) 吸声系数

下载: 全尺寸图片幻灯片

图 17 等效穿孔率对比 (a) 传递损失; (b) 吸声系数

下载: 全尺寸图片幻灯片

表 1 平板声衬结构参数

穿孔率 σ 板厚 t (mm) 孔径 d (mm) 背腔深度 b (mm)

1% 1 0.5 25

下载: 导出CSV

表 2 声衬段结构参数

管径 R (mm) 声衬段长度 L (mm) 穿孔率 σ 板厚 t (mm) 孔径 d (mm) 背腔深度 b (mm)

100 300 2% 0.87 1.83 25

下载: 导出CSV

表 3 波纹穿孔板几何参数

板长 λ (mm) 12.5 15 20 25

板高 h (mm) θ = 0° 0.55 0.66 0.88 1.10
θ = 30° 1.80 2.17 2.89 3.61
θ = 50° 3.72 4.47 5.96 7.45

下载: 导出CSV

表 4 波纹穿孔板几何参数

板长 λ (mm) 30 50 75 150

板高 h (mm) θ = 25° 3.50 5.83 8.74 17.50
θ = 35° 5.25 8.75 13.13 26.26

下载: 导出CSV

表 5 等效穿孔率验证参数

波纹板序号波纹板板长 λ (mm) 波纹板板高 h (mm) 波纹板穿孔率 σ (%) 等效穿孔率 σ' (%)

波纹板 1 300 15 2 2.05
波纹板 2 100 10 2 2.18
波纹板 3 30 5 2 2.47

下载: 导出CSV

参考文献(21)

[1]	Lieuwen T C, Yang V. Combustion instabilities in gas turbine engines: Operational experience, fundamental mechanisms, and modeling. Alexander Bell Drive, VA: American Institute of Aeronautics and Astronautics, University of Nottingham, 2005: 3—24
[2]	Culick F E. Unsteady motions in combustion chambers for propulsion systems. Neuilly, NATO: The Research and Technology Organisation of NATO, 2006: 5—17
[3]	Poinsot T. Prediction and control of combustion instabilities in real engines. Proc. Combust. Inst., 2017; 36(1): 1—28 DOI: 10.1016/j.proci.2016.05.007
[4]	Lahiri C, Bake F. A review of bias flow liners for acoustic damping in gas turbine combustors. J. Sound Vib., 2017; 400: 564—605 DOI: 10.1016/j.jsv.2017.04.005
[5]	Gullaud E, Nicoud F. Effect of perforated plates on the acoustics of annular combustors. AIAA J., 2012; 50(12): 2629—2642 DOI: 10.2514/1.J050716
[6]	Bellucci V, Flohr P, Paschereit C, et al. On the use of Helmholtz resonators for damping acoustic pulsations in industrial gas turbines. J. Eng. Gas Turbines Power, 2004; 126(2): 271—275 DOI: 10.1115/1.1473152
[7]	Dupere I D, Dowling A P. The use of Helmholtz resonators in a practical combustor. J. Eng. Gas Turbines Power, 2005; 127(2): 268—275 DOI: 10.1115/1.1806838
[8]	Bothien M R, Noiray N, Schuermans B. A novel damping device for broadband attenuation of low-frequency combustion pulsations in gas turbines. J. Eng. Gas Turbines Power, 2014; 136(4): 041504 DOI: 10.1115/1.4025761
[9]	Sohn C H, Ju H P. A comparative study on acoustic damping induced by half-wave, quarter-wave, and Helmholtz resonators. Aerosp. Sci. Technol., 2011; 15(8): 606—614 DOI: 10.1016/j.ast.2010.12.004
[10]	Zhao D, Li X Y. A review of acoustic dampers applied to combustion chambers in aerospace industry. Prog. Aerosp. Sci., 2015; 74: 114—130 DOI: 10.1016/j.paerosci.2014.12.003
[11]	Carlton T J, Thinkham N R. Means for eliminating screech in jet propulsion systems: US 3041836 A. 1962-07-03
[12]	Jiang C Y, Huang L X. Characterization of low-frequency acoustic wave propagation through a periodic corrugated waveguide. J Sound Vib., 2018; 418: 79—99 DOI: 10.1016/j.jsv.2017.12.024
[13]	Wang C Q, Liu X. Investigation of the acoustic properties of corrugated micro-perforated panel backed by a rigid wall. Mech. Syst. Signal Process., 2020; 140: 106699 DOI: 10.1016/j.ymssp.2020.106699
[14]	COMSOL AB, Stockholm, Sweden. COMSOL Multiphysics® v. 5.1. https://cn.comsol.com
[15]	杜功焕, 朱哲民, 龚秀芬. 声学基础. 第3版. 南京: 南京大学出版社, 2012: 183—185
[16]	辛博. 切向流对声衬声阻抗的影响及声衬表面非稳定波机理的研究. 博士学位论文, 北京: 北京航空航天大学, 2019: 79—81
[17]	全国声学标准化委员会. 声学阻抗管中吸声系数和声阻抗的测量, 第2部分传递函数法: GB/T 18696.2-2002. 北京: 中国标准出版社, 2002: 8—9
[18]	王晓宇. 传递单元方法及其在航空发动机短舱声学问题中的应用. 博士学位论文, 北京: 北京航空航天大学, 2010: 54—55
[19]	Namba M, Fukushige K. Application of the equivalent surface source method to the acoustics of duct systems with non-uniform wall impedance. Prog. Aerosp. Sci., 1980; 73(1): 125—146 DOI: 10.1016/0022-460X(80)90497-6
[20]	Morfey C L. Sound transmission and generation in ducts with flow. J Sound Vib., 1971; 14(1): 37—55 DOI: 10.1016/0022-460X(71)90506-2
[21]	Allam S, Abom M. A new type of muffler based on microperforated tubes. J. Vib. Acoust., 2011; 133(3): 031005 DOI: 10.1115/1.4002956

施引文献(2)

期刊类型引用(1)

岳峰丽，董磊，王楷焱，蒋从双，宋鲁涛. 微缝吸声板吸声性能探讨. 沈阳理工大学学报. 2024(04): 86-91 .

百度学术

其他类型引用(1)

资源附件(0)

图(17) / 表(5)

计量

文章访问数: 233
HTML全文浏览量: 20
PDF下载量: 43
被引次数: 2

引言
1. 理论模型
1.1 平面波垂直入射
1.2 平面波掠入射
2. 模型验证
2.1 平面波垂直入射
2.2 平面波掠入射
3. 结果分析
3.1 平面波垂直入射
3.1.1 夹角θ的影响
3.1.2 等效穿孔率与背腔
3.2 平面波掠入射
3.2.1 夹角θ的影响
3.2.2 板高h和板长λ的影响
3.2.3 等效参数研究
4. 结论

引言
1. 理论模型
1.1 平面波垂直入射
1.2 平面波掠入射
2. 模型验证
2.1 平面波垂直入射
2.2 平面波掠入射
3. 结果分析
3.1 平面波垂直入射
3.1.1 夹角θ的影响
3.1.2 等效穿孔率与背腔
3.2 平面波掠入射
3.2.1 夹角θ的影响
3.2.2 板高h和板长λ的影响
3.2.3 等效参数研究
4. 结论

参考文献(21)

施引文献

资源附件(0)

波纹穿孔板吸声特性研究

通讯作者: 刘传洋, liuchuanyang@buaa.edu.cn

计量

出版历程

Research on sound absorption characteristics of corrugated perforated plate

引言

1. 理论模型

1.1 平面波垂直入射

1.2 平面波掠入射

2. 模型验证

2.1 平面波垂直入射

2.2 平面波掠入射

3. 结果分析

3.1 平面波垂直入射

3.1.1 夹角θ的影响

3.1.2 等效穿孔率与背腔

3.2 平面波掠入射

3.2.1 夹角θ的影响

3.2.2 板高h和板长λ的影响

3.2.3 等效参数研究

4. 结论

期刊类型引用(1)

其他类型引用(1)

计量

出版历程

目录

引言

1. 理论模型

1.1 平面波垂直入射

1.2 平面波掠入射

2. 模型验证

2.1 平面波垂直入射

2.2 平面波掠入射

3. 结果分析

3.1 平面波垂直入射

3.1.1 夹角θ的影响

3.1.2 等效穿孔率与背腔

3.2 平面波掠入射

3.2.1 夹角θ的影响

3.2.2 板高h和板长λ的影响

3.2.3 等效参数研究

4. 结论

通讯作者:
刘传洋, liuchuanyang@buaa.edu.cn