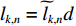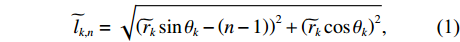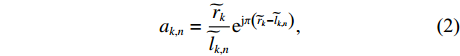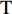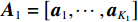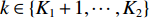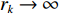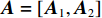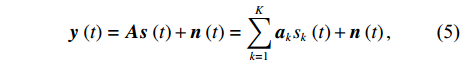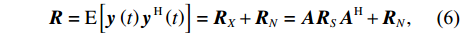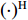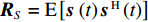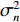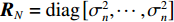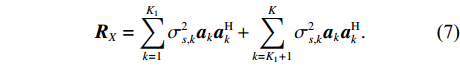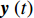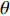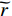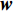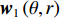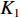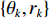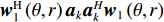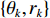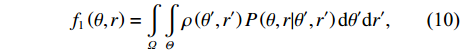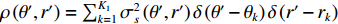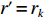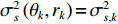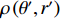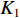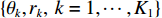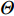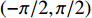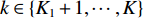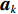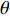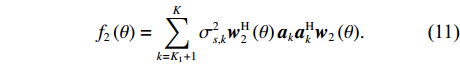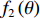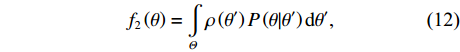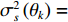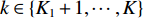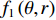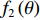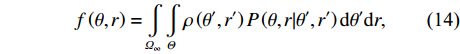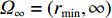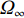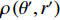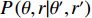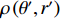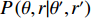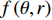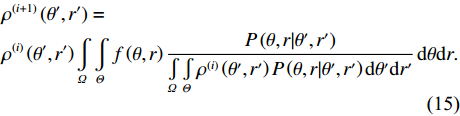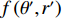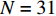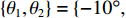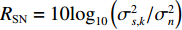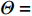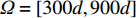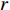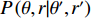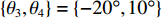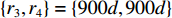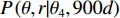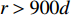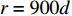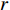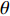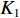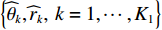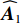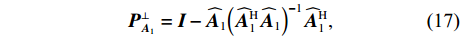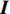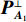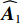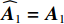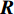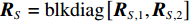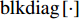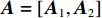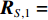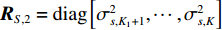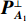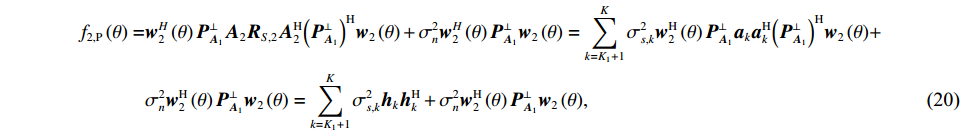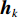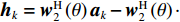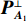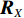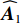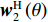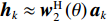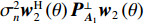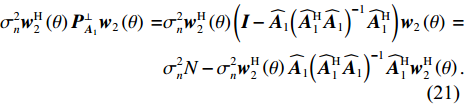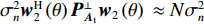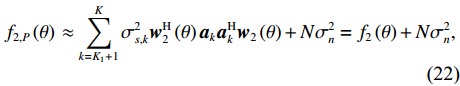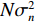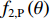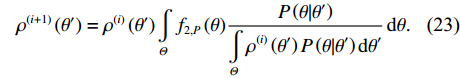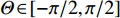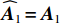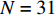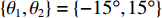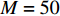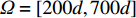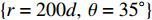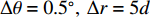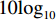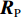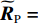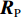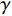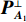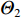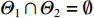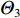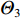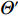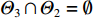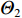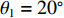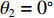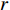Localizing mixed far- and near-field sources using beamforming deconvolution techniques
-
摘要:
提出了定位远近场混合源的波束解卷积技术, 针对非相干远近场混合声信号的线列阵观测结果, 推导了其常规波束形成(CBF)空间谱中固有的广义二维卷积数学关系, 利用Richardson-Lucy算法实现波束能量聚焦以获得近场目标的精确空域参数估计, 通过混合源协方差矩阵向近场流形的正交补空间投影操作提取远场分量, 并分析得到其内在的一维卷积关系, 然后通过角度域波束解卷积进行远场信号的波达估计。仿真分析表明, 所提方法提升了CBF谱的空域分辨力, 通过投影映射隔离近场分量后实现了混合源的分离。与现有方案相比, 所提算法针对远场信源可实现10 dB的背景噪声级抑制。
Abstract:A beam deconvolution technique for the location of the mixed far- and near-field sources is presented in this paper. The generalized two-dimensional convolution formalism inherent in the conventional beamforming (CBF) spatial spectrum yielded by the linear array observations for noncoherent mixed signals is derived. The Richardson-Lucy algorithm is exploited to focus beam power and obtain accurate spatial parameters of the near-field sources. The far-field components are extracted by mapping the mixed-source covariance matrix to the near-field manifold’s orthogonal complement space. The intrinsic one-dimensional convolution relationship is revealed. Hence, the angular domain beamforming deconvolution is used to estimate the far-field signals’ incident angles. The simulation results show that the proposed method improves the spatial resolution of the CBF spectrum and can separate the mixed sources after isolating the near-field components by projection mapping. Besides, a background noise level suppression of 10 dB for the far-field sources is achieved by comparing it with the existing schemes.
-
Keywords:
- Passive location /
- Far-field source /
- Near-field source /
- Deconvolved beamforming
-
引言
估计信号的波达方向(DOA)是阵列处理的核心任务之一, 也是众多水下应用不可或缺的一环。作为经典的解决方案, 常规波束形成(CBF)方法虽然性能相对稳健, 但较宽的主瓣与较高的旁瓣限制了其在实际工程中的应用。为此, 能够突破瑞利极限的高分辨空间谱估计方法在近几十年内受到了学者们的广泛关注, 例如最小方差无失真响应(MVDR)波束形成[1]、多重信号分类(MUSIC)方法[2]等。但是, 无论是前者通过协方差矩阵求逆以构建加权向量, 还是后者对协方差矩阵进行特征分解以获得彼此正交的信号、噪声子空间, 这种对统计特性的严重依赖都使得算法对信号失配敏感。然而, 基于CBF的解卷积方法, 在能够锐化主瓣、抑制旁瓣的同时, 也继承了CBF宽容性较强的优点, 对小快拍数、低信噪比、和阵元位置失配场景具有较强的鲁棒性。近几十年来, 解卷积技术已在信道均衡、图像处理、地震勘探、空气声源定位、功率谱估计等多个领域得到广泛应用[3], 并在最近几年被引入到水下声呐信号处理中, 成为新兴的研究热点[4–8], 关注之一便是声场的传播模型: (1) 在远场信源假设中, 认为在阵列接收处声波以平面波前扩展, 此时信号的入射角度是待求参数; (2) 在近场信源假设中, 由于传播距离近, 声波以球面波形式到达阵列, 因此要实现对目标的精确定位, 就需同时估计信源的方向和距离。
就算法层面而言, 针对远场信源, Yang分别建立了基于水平线列阵[9]和圆环阵[10]的观测信号卷积模型, 表明阵列的CBF输出可视为阵列指向性函数(对应于解卷积理论中的点扩散函数, Point Spread Function, PSF)和信源空域能量分布(即目标函数)的卷积, 且PSF在角度域或角度正弦域内保持移不变特性。将经典的解卷积技术——Richardson–Lucy (R-L)算法[11-12]应用于上述模型, 可根据已知(预测)的PSF近似重建出嵌入在CBF谱中的目标函数。因为是点状信源, 所以理论上的目标函数表现为角度域上的多个
δ 冲击, 位于真实的目标信号到达方位, 相比传统的CBF谱自然将具有更高的空域分辨力。此外, 许多研究精力也投入到开发适用于近场信源的波束解卷积方法中[13-14], 这一方面是出于对实际需求的考虑(如水下声图测量), 另一方面则是不同于远场情况下的纯方位估计, 近场模型将同时与波达方向和信源距离相关。为解决上述问题, 可通过预存角度−距离二阶字典矩阵的方式来利用R-L算法获得目标的空域能量分布[15], 但该方法计算负担较大。一种基于目标反射强度的非等间距重采样方案被提出[16], 以实现求解精度与计算代价间的最优权衡。考虑到近场PSF的移变特性, 文献[17]提出采用扩展R-L算法进行反卷积求解, 以进一步提高测量精度。然而, 在实际水下应用中, 严格的远场、近场假设条件可能无法被精确满足, 针对远近场混合源的定位算法吸引了越来越多的关注[18-22]。不同于现有的基于累积量或子空间的方法, 本文中提出一种改进的波束解卷积方法, 其动机来源于以下三点: (1) 近场和远场目标可能同时出现在阵列的监测空间内, 彼此间的相互干扰将使得仅适用于单一模型的传统解卷积方法性能受损乃至失效; (2) 很多时候无法确定未知信源到底符合哪一种声传播模型(性能稳健的算法往往不应对未知条件施加过多的理想性约束、假设), 因此一种广泛适用的方法将在鲁棒性和实用性上体现出优势; (3) 用于近场、远场声源的波束解卷积方法存在本质上的不同, 有必要对现有的多种方法在同一使用场景内进行评估。本文中, 首先绘制针对近场信源的CBF角度−距离二维空间谱, 由于混合信源、加性噪声的存在, CBF谱存在虚影且分辨力较差。考虑到对整个空间谱进行精细的二维解卷积操作不但费时费力, 且混合信源的存在将严重干扰最终结果。为此, 提出一种计算有效的方法: 首先对该谱在稀疏网格上进行二维解卷积以减轻计算压力, 通过对主瓣所在方位的判断, 识别出近场和远场信源, 以实现对混合信源的空域分离。对近场目标, 在其附近进行精确的反卷积求解, 以提升估计精度。随后根据估计结果, 构建近场流形的正交投影算子并将其作用于协方差矩阵, 以提取远场分量。至此, 针对远场目标, 可采用经典的CBF解卷积算法进行求解。数值仿真结果表明, 所提算法与CBF和MVDR相比具有更窄的主瓣与更低的旁瓣级; 与针对单一(近场或远场)模型的解卷积算法相比, 适用范围更广, 针对混合源在空域分辨力、目标探测性能方面具有显著优势; 与现有基于子空间理论的混合源定位方法相比, 对阵元方位误差体现出更强的鲁棒性。
1. 远近场混合源条件下的卷积模型
1.1 混合信源的阵列观测模型
考虑基于等间距直线阵的一维观测模型: 假设监测空间内同时出现
K=K1+K2 个中心频率为f (对应波长为λ )、来自不同方向的窄带信号, 水平线阵由N 个相邻间距为半波长d=λ/2 的传感器构成。不失一般性, 设K 个信号中的前K1 个为位于菲涅耳区[0.62√D3/λ,2D2/λ] 内的近场信源[20], 后K2 个为位于夫琅禾费区(2D2/λ,∞) 范围内的远场信源, 这里D=(N−1)d 为阵列物理孔径。假设信源数K 先验已知[18–20,23,24], 对第k∈{1,⋯,K1} 个近场信源sk(t) , 设其波达方向为θk∈(−π/2,π/2) , 到N 个传感器的距离分别为lk,n ,n∈{1,⋯,N} , 如图1所示。参考第一阵元, 令
lk,1=rk , 进一步设rk 以d 为单位的测量值为˜rk , 即rk=˜rkd , 则lk,n 还可表示为lk,n=˜lk,nd , 其中根据图1中的几何关系:˜lk,n=√(˜rksinθk−(n−1))2+(˜rkcosθk)2, (1) 为避免注意力的分散, 可移除第
n 个阵元的空域响应ak,n 对频率参数f 的显性依附, 将其简洁地表示为ak,n=˜rk˜lk,nejπ(˜rk−˜lk,n), (2) 其中, 系数项
˜rk/˜lk,n 体现了近场信号按球面波扩展时引起的幅度衰减。根据式(2), 记{{\boldsymbol{a}}}_{k}={\left[{a}_{k,1}.\cdots ,{a}_{k,N}\right]}^{{\rm{T}}}, k= 1,2,\cdots ,{K}_{1} 为近场信源的导向矢量({\rm{T}} 为转置符号), 相应的阵列流形则可表示为{{\boldsymbol{A}}_1} = \left[ {{{\boldsymbol{a}}_1}, \cdots ,{{\boldsymbol{a}}_{{K_1}}}} \right] 。对远场信源而言,
k \in \left\{ {{K_1} + 1, \cdots ,{K_2}} \right\} , 有{r_k} \to \infty ,{r_k} - {l_{k,n}} \to \left( {n - 1} \right)d\sin {\theta _k} 。此时导向矢量{{\boldsymbol{a}}_k} 和远场流形{{\boldsymbol{A}}_2} 可分别表示为{{\boldsymbol{a}}_k} = {\left[ {1,{{\rm{e}}^{{\rm{j}}\pi \sin {\theta _k}}}, \cdots ,{{\rm{e}}^{j\pi \left( {N - 1} \right)\sin {\theta _k}}}} \right]^{\rm{T}}},\;k = {K_1} + 1,{K_1} + 2, \cdots ,K, (3) {{\boldsymbol{A}}_2} = \left[ {{{\boldsymbol{a}}_{{K_1} + 1}}, \cdots ,{{\boldsymbol{a}}_K}} \right]. (4) 基于
{{\boldsymbol{A}}_1} 和{{\boldsymbol{A}}_2} , 可构建全局增广流形矩阵{\boldsymbol{A}} = \left[ {{{\boldsymbol{A}}_1},{{\boldsymbol{A}}_2}} \right] 。记信号向量为
{\boldsymbol{s}}\left( t \right) = [ {s_1}\left( t \right), \cdots ,{s_{{K_1}}}\left( t \right),{s_{{K_1} + 1}}\left( t \right), \cdots , {s_K}\left( t \right) ]^{\rm{T}} , 假设K 个窄带观测信号在接收端已经下变频与低通滤波处理。据此, 不失一般性, 包络信号s\left( t \right) 被建模为K 个彼此统计独立的零均值复高斯随机过程, 可由方差\left\{ {\sigma _{s,k}^2,\;\;k = 1, \cdots ,K} \right\} 完全表征。此时, 阵列对远近场混合源的观测结果应是对K 个信源空域响应的叠加, 其观测模型为{\boldsymbol{y}}\,\left( t \right) = {\boldsymbol{As}}\,\left( t \right) + {\boldsymbol{n}}\,\left( t \right) = \sum\limits_{k = 1}^K {{{\boldsymbol{a}}_k}{s_k}} \,\left( t \right) + {\boldsymbol{n}}\,\left( t \right), (5) 式中
{\boldsymbol{n}}\,\left( t \right) 为N 个通道的观测噪声。假设信号与噪声相互独立, 估计
{\boldsymbol{ y}}\,\left( t \right) 的协方差矩阵有{\boldsymbol{R}} = {\rm{E}}\left[ {{\boldsymbol{y}}\,\left( t \right) {\boldsymbol{y}}{\,^{\rm{H}}}\left( t \right)} \right] = {{\boldsymbol{R}}_X} + {{\boldsymbol{R}}_N} = {\boldsymbol{A}}{{\boldsymbol{R}}_S}{{\boldsymbol{A}}^{\rm H}} + {{\boldsymbol{R}}_N}, (6) 上式中,
{\rm{E}}\left[ \cdot \right] 表示期望运算,{( \cdot )^{\rm H}} 代表共轭转置操作。{{\boldsymbol{R}}_X} = {\boldsymbol{A}}{{\boldsymbol{R}}_S}{{\boldsymbol{A}}^{\rm{H}}} 是无噪声情况下的理想协方差矩阵,{{\boldsymbol{R}}_S} = {\rm{E}}\left[ {{\boldsymbol{s}}\,\left( t \right) {\boldsymbol{s}}{\,^{\rm{H}}}\left( t \right)} \right] , 根据信号独立假设, 它可进一步表示为{{\boldsymbol{R}}_S} = {\rm{diag}}\left[ {\sigma _{s,1}^2, \cdots ,\sigma _{s,K}^2} \right] , 其中{\rm{diag}}\left[ \cdot \right] 表示对角矩阵,\sigma _{s,k}^2 为第k 个信号的功率。{{\boldsymbol{R}}_N} = {\rm{E}}\left[ {{\boldsymbol{n}}\,\left( t \right) {\boldsymbol{n}}{\,^{\rm{H}}}\left( t \right)} \right] 是噪声协方差矩阵, 对方差为\sigma _n^2 的空域加性噪声而言,{{\boldsymbol{R}}_N} = {\rm{diag}}\left[ {\sigma _n^2, \cdots ,\sigma _n^2} \right] 。至此, 式(6)中的{{\boldsymbol{R}}_X} 可化简为{{\boldsymbol{R}}_X} = \sum\limits_{k = 1}^{{K_1}} {\sigma _{s,k}^2{{\boldsymbol{a}}_k}{\boldsymbol{a}}_k^{\rm H}} + \sum\limits_{k = {K_1} + 1}^K {\sigma _{s,k}^2{{\boldsymbol{a}}_k}{\boldsymbol{a}}_k^{\rm H}} . (7) 实际中, 当对信号进行
M 次采样得到样本\left\{ {{\boldsymbol{y}}\,\left( {{t_m}} \right),\;m = 1, \cdots ,M} \right\} 后,{\boldsymbol{y}}\,\left( t \right) 的采样协方差矩阵可按如下方式计算:\widehat {\boldsymbol{R}} = \frac{1}{M}\sum\limits_{m = 1}^M {{\boldsymbol{y}}\,\left( {{t_m}} \right) {\boldsymbol{y}}{\,^{\rm{H}}}\left( {{t_m}} \right)} . (8) 1.2 基于常规波束形成的卷积模型
CBF的目的在于利用权向量
{\boldsymbol{w}} 调整各阵元间的相位差以实现对信号的相干接收。对近场源而言, 从式(2)中可以看出, 同一信号在各通道间的相位差不但与入射角度\theta 有关, 同时也是半径\widetilde r 的函数。因此,{\boldsymbol{w}} 也应是一个二变元函数, 记为{{\boldsymbol{w}}_1}\left( {\theta ,r} \right) , 基于式(2)构造。因此, 对{K_1} 个近场源的CBF输出可表示为{f_1}\left( {\theta ,r} \right) = \sum\limits_{k = 1}^{{K_1}} {\sigma _{s,k}^2{\boldsymbol{w}}_1^{\rm H}\left( {\theta ,r} \right){{\boldsymbol{a}}_k}{\boldsymbol{a}}_k^{\rm{H}}{{\boldsymbol{w}}_1}\left( {\theta ,r} \right)} . (9) 考虑到导向矢量
{{\boldsymbol{a}}_k} 应是\left\{ {{\theta _k},{r_k}} \right\} 的函数, 则{\boldsymbol{w}}_1^{\rm{H}}\left( {\theta ,r} \right){{\boldsymbol{a}}_k}{\boldsymbol{a}}_k^H{{\boldsymbol{w}}_1}\left( {\theta ,r} \right) 可解释为在权向量{\boldsymbol{w}}_1^{\rm{H}}\left( {\theta ,r} \right) 下对\left\{ {{\theta _k},{r_k}} \right\} 处单位能量信源的CBF输出, 记为P\left( {\theta ,r|{\theta _k},{r_k}} \right) 。此时, 式(9)服从如下的二维卷积形式:{f_1}\left( {\theta ,r} \right) = \int\limits_\varOmega {\int\limits_\varTheta {\rho \left( {\theta ' ,r' } \right)P\left( {\theta ,r|\theta' ,r'} \right)\,} } {\rm{d}}\theta' {\rm{d}}r' , (10) 其中,
\rho \left( {\theta ',r' } \right) = \sum\nolimits_{k = 1}^{{K_1}} {\sigma _s^2\left( {\theta' ,r' } \right)\delta \left( {\theta ' - {\theta _k}} \right)\delta \left( {r' - {r_k}} \right)} 即为目标函数, 当\theta ' = {\theta _k} 且r' = {r_k} 时,\sigma _s^2\left( {{\theta _k},{r_k}} \right) = \sigma _{s,k}^2 。\rho \left( {\theta ' ,r' } \right) 表示{K_1} 个在\left\{ {{\theta _k},{r_k},\;k = 1, \cdots ,{K_1}} \right\} 处冲击函数的叠加, 冲击幅值分别为\left\{ {\sigma _{s,k}^2,\;k = 1, \cdots ,{K_1}} \right\} 。显然, 与CBF波束相比, 冲激函数将具有更为尖锐的“主瓣”。在式(10)中,\varTheta 和\varOmega 分别表示角度域和距离域的积分区间, 其中\varTheta 可取\left( { - \pi /2,\pi /2} \right) , 因为线列阵只能对半空间实现无模糊观测, 而\varOmega 应包括所有近场源可能存在的范围。当
k \in \left\{ {{K_1} + 1, \cdots ,K} \right\} ,{r_k} \to \infty 时, 则过渡到远场源情况。此时{{\boldsymbol{a}}_k} 只与入射角度\theta 有关, 则关于权向量{{\boldsymbol{w}}_2}\left( \theta \right) = {\lim _{r \to \infty }}{{\boldsymbol{w}}_1}\left( {\theta ,r} \right) 的CBF谱可构建为{f_2}\left( \theta \right) = \sum\limits_{k = {K_1} + 1}^K {\sigma _{s,k}^2{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right){{\boldsymbol{a}}_k}{\boldsymbol{a}}_k^{\rm{H}}{{\boldsymbol{w}}_2}\left( \theta \right)} . (11) 类似地, 令
P\left( {\theta |\theta'} \right) = {\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right){{\boldsymbol{a}}_k}{\boldsymbol{a}}_k^{\rm{H}}{{\boldsymbol{w}}_2}\left( \theta \right) ,{f_2}\left( \theta \right) 有如下的卷积表达:{f_2}\left( \theta \right) = \int\limits_\varTheta {\rho \left( {\theta ' } \right)P\left( {\theta |\theta ' } \right)} \,{\rm{d}}\theta ' , (12) 其中,
\rho \left( {\theta ' } \right) = \sum\nolimits_{k = {K_1} + 1}^K {\sigma _s^2\left( {\theta ' } \right)\delta \left( {\theta ' - {\theta _k}} \right)} , 若\theta ' = {\theta _k} ,\sigma _s^2\left( {{\theta _k}} \right) = \sigma _{s,k}^2 ,k \in \left\{ {{K_1} + 1, \cdots ,K} \right\} 。在式(10)和式(12)中, 分别回顾了近场和远场信源的CBF卷积模型。对混合源来说, 由于协方差矩阵是与各个信源有关分量的累加求和(见式(7)), 因此与之相关的卷积表达也将是现有模型的叠加, 即
f\left( {\theta ,r} \right) = {f_1}\left( {\theta ,r} \right) + {f_2}\left( \theta \right). (13) 实际上, 当
r \to \infty 时, 有{f_1}\left( {\theta ,r} \right) \to {f_2}\left( \theta \right) 。因此, 当{f_1}\left( {\theta ,r} \right) 中的距离积分区间\varOmega 包含\infty 时, 即{\varOmega _\infty } = \left( {{r_{\min }},\infty } \right) , 其中{r_{\min }} 为近场源可能存在范围的最小值, 则卷积模型{f_1}\left( {\theta ,r} \right) 自然包含了{f_2}\left( \theta \right) 。基于上述分析, 混合源的CBF输出f\left( {\theta ,r} \right) 可重新写为如下的广义二维卷积:f\left( {\theta ,r} \right) = \int\limits_{{\varOmega _\infty }} {\int\limits_\varTheta {\rho \left( {\theta ' ,r' } \right)P\left( {\theta ,r|\theta ' ,r' } \right)} } \,{\rm{d}}\theta ' {\rm{d}}r, (14) 其中
\varTheta = \left( { - \pi /2,\pi /2} \right) ,{\varOmega _\infty } = \left( {{r_{\min }},\infty } \right) 。式(14)给出了混合源存在条件下的广义CBF卷积模型。然而, 由于积分区间
{\varOmega _\infty } 的界定, 导致CBF空间谱的绘制与相应的解卷积运算物理上无法实现, 虽然单纯在近场或远场情况下上述操作都是可行的。为此, 下文提出一种组合式策略以解决所面临的问题。2. 基于波束解卷积的混合源定位方法
2.1 混合信源的空域分离
式(14)已将
f\left( {\theta ,r} \right) 表示为\rho \left( {\theta ' ,r' } \right) 和P\left( {\theta ,r|\theta ' ,r' } \right) 的二维卷积, 根据之前的分析, 前者\rho \left( {\theta ' ,r' } \right) 为待求的目标函数, 具有尖锐的冲击形式, 后者P\left( {\theta ,r|\theta ' ,r' } \right) 即是解卷积文献中常见的点扩散函数(即PSF), 其具体数学构造可根据阵列几何结构进行预测[15]。二者之间的卷积作用导致了\rho \left( {\theta ' ,r' } \right) 的空域“模糊”, 解卷积的目的便在于利用已知(可预测)的P\left( {\theta ,r|\theta ' ,r' } \right) 从已观测到的f\left( {\theta ,r} \right) 中恢复出目标函数\rho \left( {\theta ' ,r' } \right) 。许多算法都可实现对式(14)的反卷积求解, 但由于R-L算法具有以下优点: (1) 在低信噪比下性能更好; (2) 只需执行线性操作, 方便计算且易于分析; (3) 对相干源的旁瓣抑制能力更强, 故在水声领域得到广泛的研究与应用。R-L算法基于贝叶斯准则, 其第i 次迭代公式可表示为\begin{split}& {\rho ^{\left( {i + 1} \right)}}\left( {\theta ' ,r' } \right) = \\&{\rho ^{\left( i \right)}}\left( {\theta ' ,r' } \right)\int\limits_\varOmega {\int\limits_\varTheta {f\left( {\theta ,r} \right)\frac{{P\left( {\theta ,r|\theta ' ,r' } \right)}}{{\int\limits_\varOmega {\int\limits_\varTheta {{\rho ^{\left( i \right)}}\left( {\theta ' ,r' } \right)P\left( {\theta ,r|\theta ' ,r' } \right)} } \,{\rm{d}}\theta ' {\rm{d}}r' }}} } \,{\rm{d}}\theta {\rm{d}}r. \end{split} (15) 算法初始化可选择
{\rho ^{\left( 0 \right)}}\left( {\theta ' ,r' } \right) = f\left( {\theta ' ,r' } \right) , 即所得到的CBF空间谱。f\left( {\theta ' ,r' } \right) 可在菲涅耳区内进行计算, 其结果不但会反映近场信源的空域能量分布, 同时也会受到远场信源的干扰, 遭受严重的空域模糊。为此, 可采用文献[15]提出的反卷积算法来改善空间谱的质量, 但由于此方法需预存求解空间中所有的字典矩阵, 即依次对P\left( {\theta ,r|\theta ' ,r' } \right) 中的参数\left\{ {\theta ,r,\theta ' ,r' } \right\} 在空间\left\{ {\varOmega ,\varTheta ,\varOmega ,\varTheta } \right\} 中进行遍历, 相应数据将存放于四阶张量中, 因此计算复杂度较大。考虑到此步的目的是分离混合信源并进一步确定近场信源的所在范围, 因此所选的求解网格点可适当稀疏以缓解计算压力。图2仿真中, 令
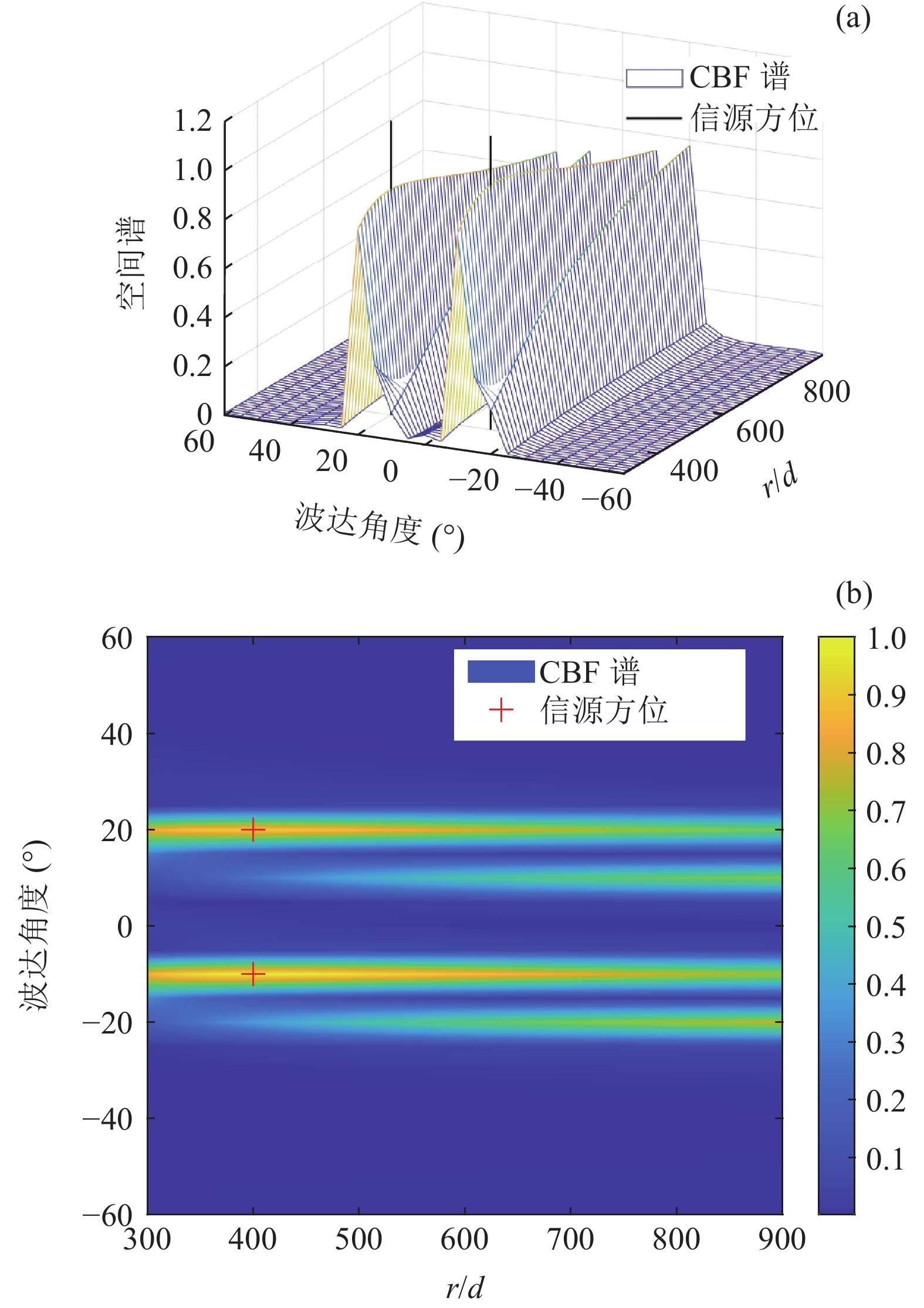
N = 31 , 两近场源\{{\theta }_{1},{\theta }_{2}\}= \{-10\text{°}, 20\text{°}\} ,\left\{ {{r_1},{r_2}} \right\} = \left\{ {400d,400d} \right\} , 两远场源\left\{{\theta }_{3},{\theta }_{4}\right\}=\{-20\text{°}, 10\text{°}\} 。定义信噪比{R_{{\text{SN}}}} = 10{\log _{10}}\left( {\sigma _{s,k}^2/\sigma _n^2} \right) , 并设其均为10 dB, 基于M = 100 次快照, 在求解区域\varTheta = \left[ { - 60^\circ ,60^\circ } \right] ,\varOmega = \left[ {300d,900d} \right] 内选取\Delta \theta = {5^\circ },\;\Delta r = 10d (\Delta \theta 和\Delta r 分别代表角度域和距离域的网格划分单位)进行稀疏网格划分, 对应的CBF空间谱如图2所示, 图中标出了两个近场信源的所在方位。可以发现, 近场信源的CBF峰值在其真实方位附近, 而随着距离r 的增加, 远场信源的CBF输出逐渐增大, 这是因为此时P\left( {\theta ,r|\theta ' ,r' } \right) 将逐渐趋近于P\left( {\theta |\theta ' } \right) 。然而, 同样可以看出: (1) CBF谱在距离域上存在大范围模糊, 严重影响对信源的定位; (2) 远场信源会对近场信源造成一定程度的干扰, 以致产生误判。为改善图2质量, 进行上述二维解卷积操作, 经过200次迭代得到图3。由图3可知, 解卷积后的空间谱对距离参数
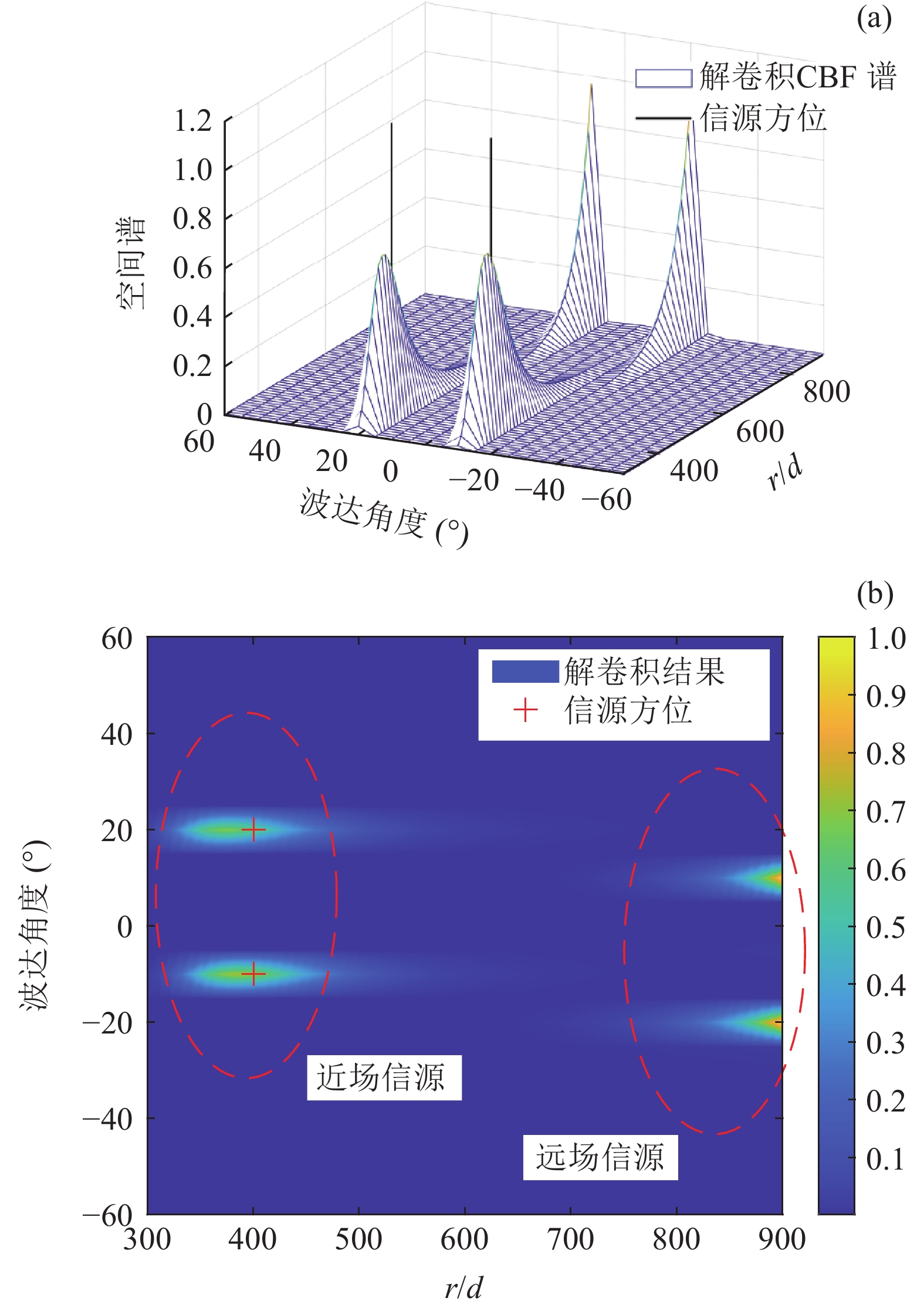
r 的分辨力明显增强, 明确给出了两个近场信源所处的大致方位。但由于所划分网格较为稀疏, 因此估计结果与真实值存在一定误差, 后续可在该估计值附近进行进一步的精确求解。此外, 还观察到在\left\{{\theta }_{3},{\theta }_{4}\right\}=\left\{-20\text{°}, 10\text{°}\right\} ,\left\{ {{r_3},{r_4}} \right\} = \left\{ {900d,900d} \right\} (即求解空间边界处)附近出现两个尖锐谱峰, 该现象与远场信源有关。因为解卷积算法总是在现有的字典库P\left( {\theta ,r|\theta ' ,r' } \right) ,\theta ' \in \left[ { - 60^\circ ,60^\circ } \right] ,r' \in \left[ {300d,900d} \right] 中寻找合适的PSF以“解释”图2中的CBF输出结果, 作为对求解空间边缘上两个谱峰的“回应”, 与两个远场信源关系最为密切的P\left( {\theta ,r|{\theta _3},900d} \right) 和P\left( {\theta ,r|{\theta _4},900d} \right) 被用来解释其成因, 因此图3的相应位置出现虚影。它由图像的突然截断所导致, 因为缺少后续r > 900d 的空间谱信息, 本应在r \to \infty 处的目标函数在截断处r = 900d 被重建。上述观察给出了近场、远场信源的判别依据, 且解卷积结果实现了两种信源的空域分离。至此, 混合源的反卷积问题可转换为两个子问题, 即针对近场和远场信源分别进行精确求解。
2.2 近场、远场信源的精确求解
对于近场目标, 由于图3中的反卷积谱已给出其大致方位, 因此可在现有结果的附近进行精细的网格划分, 随后执行反卷积计算。这样做的好处是: (1) 求解区域的缩小有效降低了计算复杂度, 对二维情况更是如此; (2) 缩小后的区域所包含的远场信源能量更少, 因此对最终所得结果的干扰也就越小; (3) 更为精细的网格划分将有助于估计精度的提升。
在完成对近场目标的参数估计后, 后续任务是如何得到远场信源的入射方向。需要注意的是, 直接对混合信源进行远场CBF测向, 则所得结果也会受到近场目标的干扰。与近场情况不同, 远场测向时距离维度
r 已被忽略, 所得CBF谱仅是\theta 的函数。更少的特征维度导致单纯依靠一维CBF波形难以在存在近场干扰时有效获取远场分量。考虑到以上问题, 采用构建正交投影算子的方法以实现对近场信号分量的抑制。设最终对
{K_1} 个近场源的空域参数估计结果为\left\{ {{{\widehat \theta }_k},{{\widehat r}_k},\;k = 1, \cdots ,{K_1}} \right\} , 则根据式(2)可重构近场流形矩阵{{\boldsymbol{A}}_1} 为{\widehat {\boldsymbol{A}}_1} = \left[ {{\boldsymbol{a}}\left( {{{\widehat \theta }_1},{{\widehat r}_1}} \right), \cdots ,{\boldsymbol{a}}\left( {{{\widehat \theta }_{{K_1}}},{{\widehat r}_{{K_1}}}} \right)} \right], (16) 再根据
{\widehat {\boldsymbol{A}}_1} , 构造相应的正交投影矩阵为{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot = {\boldsymbol{I}} - {\widehat {\boldsymbol{A}}_1}{\left( {\widehat {\boldsymbol{A}}_1^{\rm{H}}{{\widehat {\boldsymbol{A}}}_1}} \right)^{ - 1}}\widehat {\boldsymbol{A}}_1^{\rm{H}}, (17) 其中, 上标“−1”表示矩阵求逆,
{\boldsymbol{I}} 表示单位矩阵。{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot 表示到{\widehat {\boldsymbol{A}}_1} 正交补空间上的投影。若得到近场参数的理想估计, 即{\widehat {\boldsymbol{A}}_1} = {{\boldsymbol{A}}_1} , 则将{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot 左乘增广流形{\boldsymbol{A}} , 有{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {\boldsymbol{A}} = \left[ {{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{A}}_1},{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{A}}_2}} \right] = \left[ {{\mathbf{0}},{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{A}}_2}} \right]. (18) 将
{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot 作用于协方差矩阵{\boldsymbol{R}} , 并注意到{{\boldsymbol{R}}_S} 可划分为{{\boldsymbol{R}}_S} = {\rm{blkdiag}}\left[ {{{\boldsymbol{R}}_{S,1}},{{\boldsymbol{R}}_{S,2}}} \right] , 此处{\rm{blkdiag}}\left[ \cdot \right] 表示分块对角矩阵, 与流形矩阵{\boldsymbol{A}} = \left[ {{{\boldsymbol{A}}_1},{{\boldsymbol{A}}_2}} \right] 的构建相对应,{{\boldsymbol{R}}_{S,1}} = {\rm{ diag}}\left[ {\sigma _{s,1}^2, \cdots ,\sigma _{s,{K_1}}^2} \right] 和{{\boldsymbol{R}}_{S,2}} = {\rm{diag}}\left[ {\sigma _{s,{K_1} + 1}^2, \cdots ,\sigma _{s,K}^2} \right] 分别包含{K_1} 个近场信源和{K_2} 个远场信源的功率, 最终有\begin{split} {{\boldsymbol{R}}_P} = & {\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{R}}_X}{\left( {{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot } \right)^{\rm{H}}} + {\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{R}}_N}{\left( {{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot } \right)^{\rm{H}}} = {\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{A}}_1}}&{{{\boldsymbol{A}}_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{R}}_{S,1}}}&{}\\ {}&{{{\boldsymbol{R}}_{S,2}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{A}}_1^{\rm{H}}}\\ {{\boldsymbol{A}}_2^{\rm{H}}} \end{array}} \right]{\left( {{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot } \right)^{\rm{H}}} + \sigma _n^2{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {\left( {{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot } \right)^{\rm{H}}} =\\& \left[ {{\bf{0}},{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{A}}_2}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{R}}_{S,1}}}&{}\\ {}&{{{\boldsymbol{R}}_{S,2}}} \end{array}} \right] \left[ \begin{array}{l} \;\;\;\;\;\;{\bf{0}}\\ {\boldsymbol{A}}_2^{\rm{H}}{\left( {{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot } \right)^{\rm{H}}} \end{array} \right] + \sigma _n^2{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot = {\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{A}}_2}{{\boldsymbol{R}}_{S,2}}{\boldsymbol{A}}_2^{\rm{H}}{\left( {{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot } \right)^{\rm{H}}} + \sigma _n^2{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot . \end{split} (19) 式(19)说明,
{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot 的引入理论上可有效消除{{\boldsymbol{R}}_X} 中的近场信源分量。根据远场导向矢量(见式(3))构建权向量{{\boldsymbol{w}}_2}\left( \theta \right) , 对{{\boldsymbol{R}}_{\rm{P}}} 进行CBF, 有\begin{split} {f_{2,{\rm{P}}}}\left( \theta \right) = & {\boldsymbol{w}}_2^H\left( \theta \right){\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{A}}_2}{{\boldsymbol{R}}_{S,2}}{\boldsymbol{A}}_2^{\rm{H}}{\left( {{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot } \right)^{\rm{H}}}{{\boldsymbol{w}}_2}\left( \theta \right) +\sigma _n^2{\boldsymbol{w}}_2^H\left( \theta \right){\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{w}}_2}\left( \theta \right) = \sum\limits_{k = {K_1} + 1}^K {\sigma _{s,k}^2{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right) {\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{a}}_k}{\boldsymbol{a}}_k^{\rm{H}} {{\left( {{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot } \right)}^{\rm{H}}}{{\boldsymbol{w}}_2}\left( \theta \right)} +\\& \sigma _n^2{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right){\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{w}}_2}\left( \theta \right) =\sum\limits_{k = {K_1} + 1}^K {\sigma _{s,k}^2{{\boldsymbol{h}}_k}{\boldsymbol{h}}_k^{\rm{H}} + \sigma _n^2{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right){\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{w}}_2}\left( \theta \right)} , \end{split} (20) 其中,
{{\boldsymbol{h}}_k} = {\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right) {\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{a}}_k} 。进一步分析有: 依据式(17)中的定义对{{\boldsymbol{h}}_k} 展开, 可知{{\boldsymbol{h}}_k} = {\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right){{\boldsymbol{a}}_k} - {\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right)\cdot {\widehat {\boldsymbol{A}}_1}{\left( {\widehat{\boldsymbol{ A}}_1^{\rm{H}}{{\widehat {\boldsymbol{A}}}_1}} \right)^{ - 1}}\widehat{\boldsymbol{ A}}_1^{\rm{H}}{{\boldsymbol{a}}_k} 包含两项, 第1项是未经投影矩阵{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot 作用时直接对{{\boldsymbol{R}}_X} 进行CBF得到的数学表达, 第2项可解释为{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right) 和{{\boldsymbol{a}}_k} 在近场流形矩阵{\widehat {\boldsymbol{A}}_1} 列空间上的投影, 由于此处的{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right) 和{{\boldsymbol{a}}_k} 均是远场导向矢量, 与近场流形相关性较弱, 因此第2项的投影结果远小于第1项, 即{{\boldsymbol{h}}_k} \approx {\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right){{\boldsymbol{a}}_k} 。此外, 对式(20)中的第2项\sigma _n^2{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right){\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{w}}_2}\left( \theta \right) 展开, 有\begin{split} \sigma _n^2{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right){\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{w}}_2}\left( \theta \right)\, =& \sigma _n^2{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right)\left( {{\boldsymbol{I}} - {{\widehat {\boldsymbol{A}}}_1}{{\left( {\widehat {\boldsymbol{A}}_1^{\rm{H}}{{\widehat {\boldsymbol{A}}}_1}} \right)}^{ - 1}}\widehat {\boldsymbol{A}}_1^{\rm{H}}} \right){{\boldsymbol{w}}_2}\left( \theta \right)\, = \\&\sigma _n^2N - \sigma _n^2{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right){{\widehat {\boldsymbol{A}}}_1}{\left( {\widehat {\boldsymbol{A}}_1^{\rm{H}}{{\widehat {\boldsymbol{A}}}_1}} \right)^{ - 1}}\widehat {\boldsymbol{A}}_1^{\rm{H}}{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right). \end{split} (21) 注意到
{{\boldsymbol{w}}_2}\left( \theta \right)\, 是远场信源的导向矢量, 与上述分析类似, 上式中第2项的数值应远小于第1项, 即\sigma _n^2{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right){\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot {{\boldsymbol{w}}_2}\left( \theta \right)\, \, \approx N\sigma _n^2 。故有
{f_{2,P}}\left( \theta \right)\, \approx \sum\limits_{k = {K_1} + 1}^K {\sigma _{s,k}^2{\boldsymbol{w}}_2^{\rm{H}}\left( \theta \right) {{\boldsymbol{a}}_k}{\boldsymbol{a}}_k^{\rm{H}} {{\boldsymbol{w}}_2}\left( \theta \right)} + N\sigma _n^2 = {f_2}\left( \theta \right) + N\sigma _n^2, (22) 近似为式(11)中的CBF输出与常数项
N\sigma _n^2 的加和, 其卷积形式由式(12)给出。因此可对{f_{2,{\rm{P}}}}\left( \theta \right)\, 进行经典的CBF反卷积求解。由于此时{f_{2,{\rm{P}}}}\left( \theta \right)\, 中已不包含近场信源分量, 因此所得结果是无歧义的。基于式(12)的一维R-L算法可表述为{\rho ^{\left( {i + 1} \right)}}\left( {\theta ' } \right) = {\rho ^{\left( i \right)}}\left( {\theta ' } \right)\int\limits_\varTheta {{f_{2,P}}\left( \theta \right)} \frac{{P\left( {\theta |\theta ' } \right)}}{{\displaystyle\int\limits_\varTheta {{\rho ^{\left( i \right)}}\left( {\theta ' } \right)P\left( {\theta |\theta ' } \right)} \,{\rm{d}}\theta ' }}\,{\rm{d}}\theta . (23) 作为上式的初始化, 令
{\rho ^{\left( 0 \right)}}\left( {\theta ' } \right) = {f_{2,{\rm{P}}}}\left( {\theta ' } \right)\, , 求解区间可设定为\varTheta \in \left[ { - \pi /2,\pi /2} \right] 。虽然如上分析均建立在{\widehat {\boldsymbol{A}}_1} = {{\boldsymbol{A}}_1} (即所得到的近场参数估计值与真实值相等)的基础之上, 这在实际测量中一般无法达到, 测量误差总是不可避免的, 但大量仿真依然验证了上述处理流程的可行性与有效性。还需要说明的是, 尽管本文推导建立在信源独立假设上, 但对于相干情况, 大部分解卷积方法仍保持良好的聚焦性能[15,25], 尤其是本文所采用的R-L算法, 它在旁瓣抑制方面具有优势。因此所提出的算法依然可应用于信源相干场景, 只是信源彼此间的相干性可能造成更为严重的旁瓣干扰, 可考虑通过提高迭代次数以缓解这种负面效应。至此, 所提算法的执行步骤可概括如下: (1) 在给定范围内(如菲涅尔区或根据先验知识所确定的近场源可能分布范围)进行适当稀疏的网格划分以得到关于角度−距离参数的二维CBF空间谱, 通过预存字典矩阵的方式对该谱执行R-L算法, 并根据求解结果划分近场和远场信源; (2) 针对所判断的近场信源, 在其附近进行精细的网格划分, 再通过上述二维R-L算法进行反卷积求解, 以得到对近场信源方位更为精确的估计; (3) 根据所获得的近场信源参数, 构建近场流形的正交投影算子, 然后将算子作用于协方差矩阵以滤去其中的近场源分量, 再根据所得结果进行远场一维CBF, 并对远场CBF谱进行解卷积操作以获得远场信源的波达方向。为更直观地呈现, 图4给出了所提算法的计算流程。
3. 仿真
仿真中通过与CBF、MVDR、LOFNS[20]和现有的波束解卷积算法[9]相对比, 评估所提算法性能, 重点研究: (1) 混合源存在下的近场、远场目标定位; (2) 存在阵列误差时算法的性能表现; (3) 近场、远场信源不同信噪比下算法的空域分辨能力。
3.1 近场信源定位结果对比
仿真条件1: 窄带声源中心频率为1000 Hz, 并通过希尔伯特变换得到其解析形式, 阵元间距为0.75 m, 阵元数
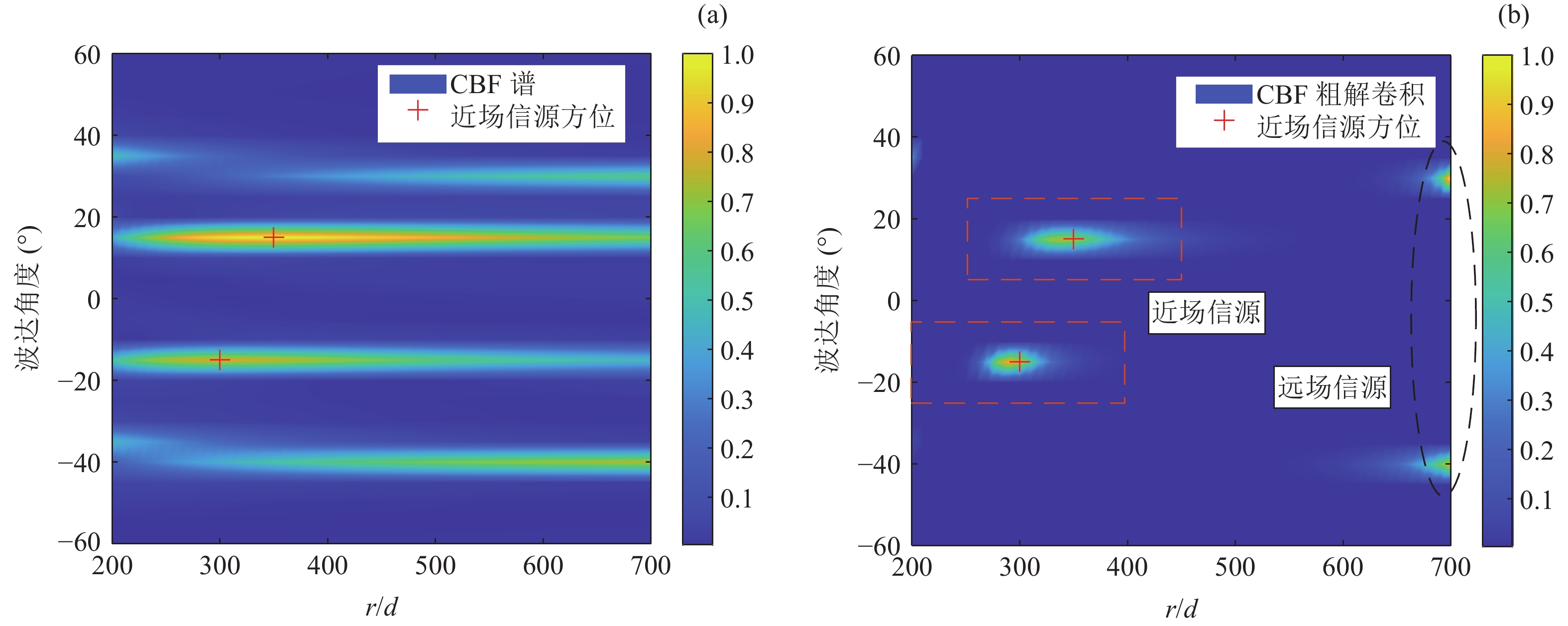
N = 31 , 两个近场信源波达参数为\left\{{\theta }_{1},{\theta }_{2}\right\}=\left\{-15\text{°}, 15\text{°}\right\} , 距离为\left\{ {{r_1},{r_2}} \right\} = \left\{ {300d,350d} \right\} , 两个远场信源入射角度为\left\{{\theta }_{3},{\theta }_{4}\right\}=\left\{-40\text{°}, 30\text{°}\right\} , 接收信噪比均设定为{R_{{\text{SN}}}} = 10\;{\rm{dB}} , 快拍数M = 50 , 解卷积次数如无特殊说明, 默认为300。首先, 计算近场二维CBF空间谱, 以得到图5(a), 其中求解区域设置为
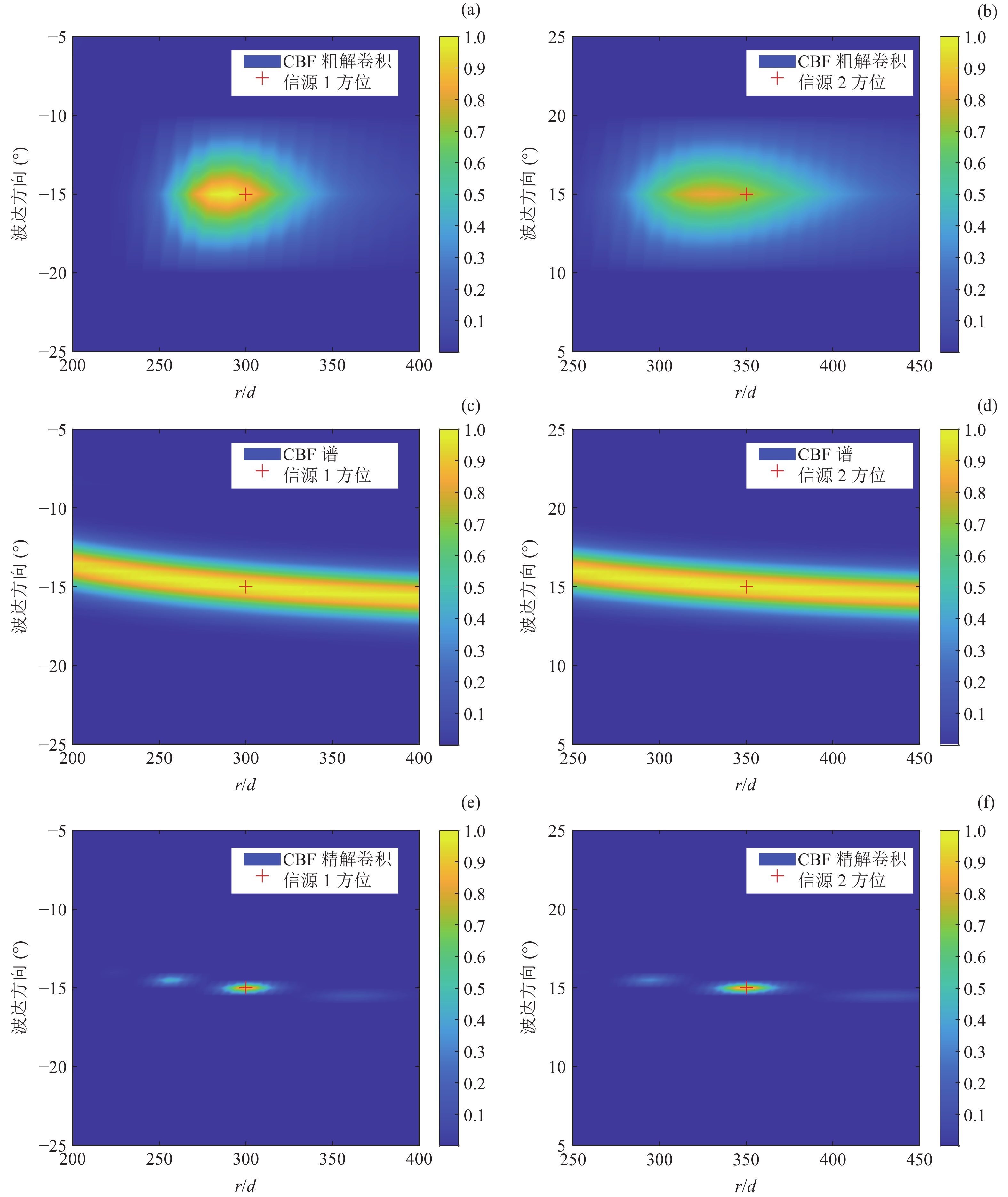
\varTheta = \left[ { - 60^\circ ,60^\circ } \right] ,\varOmega = \left[ {200d,700d} \right] , 稀疏网格按照\Delta \theta = {5^\circ },\;\Delta r = 10d 进行划分, 随后根据所得CBF谱进行反卷积求解, 结果如图5(b)所示。对比可知, 解卷积后的空间谱在距离维上空域分辨力明显提高, 图像中部两个明显的光斑标记出近场信源的大致方位, 而图像边缘的光斑按之前分析被解释为远场信源所产生的虚影。虽然图5(b)中也存在一些可能被误判为真实信源的“伪目标”, 参考\left\{ {r = 200d,\;\theta = {{35}^\circ }} \right\} 处强度较弱的旁瓣(它由图像的边缘截断效应所引起), 但由于本文先前已经假设信源数K = 4 先验已知, 因此根据常规逻辑, 依然会将图中4个最为明显的谱峰判断为真实目标, 从而排除掉其余微弱旁瓣的干扰。因此, 二维R-L算法很好地对混合信源进行了空域分离。对所识别出的近场信源, 可在其附近确定细化的求解区域, 图中已用红色方框标出。之后, 分别对两个方框区域进行更为精细的局部反卷积求解, 得到图6。图6(a)、图6(c)、图6(e)是不同算法对信源1的估计结果, 图6(b)、图6(d)、图6(f)则对应于信源2。具体地, 图6(a)(b)是基于稀疏CBF空间谱的粗反卷积结果, 即图5(b)中红框区域的放大, 对该区域进行精细网格划分, 细化的网格大小为
\Delta \theta = {0.5^\circ },\;\Delta r = 5d , 再计算相应的CBF谱得到图6(c)(d), 随后对其进行解卷积得到图6(e)(f)。图6(a)(b)图虽实现了混合信源的分离, 但空域分辨力较差, 且估计值偏离信源的真实方位, 这是因为网格划分过于稀疏。图6(c)(d)在距离维模糊严重, 即无法确定近场信源的远近, 但由于网格的精细化分, 角度域分辨力优于图6(a)(b)的粗解卷积结果。图6(e)(f)作为图6(c)(d)的反卷积结果, 空域分辨力最好, 不但进一步抑制了角度域上的CBF旁瓣, 而且消除了CBF谱中的远近模糊问题, 虽然一些伪峰依旧存在, 但峰值明显低于真实方向上的波束主瓣, 很容易根据峰值的强弱将其排除。因此, 图6(e)(f)可以给出近场信源的精确二维方位。它的优良性能一方面源自求解格点划分较密, 同时也得益于求解区域的缩小能够进一步抑制远场信源的干扰, 所带来的直观优势是在图6(e)(f)中没有出现类似于图5(b)中的边缘虚影。需要强调的是, 这种先整体粗略求解、后局部精细求解的计算策略也有效缓解了二维R-L算法所带来的计算负担。3.2 远场信源定位结果对比
根据图6(e)(f)中的估计结果, 可重构近场流形, 随后隔离协方差矩阵中的近场信源分量, 以进行远场信源的测向。图7中给出了CBF、MVDR和CBF解卷积50次后的输出结果(所有空间谱均归一化后取
10{\log _{10}} ), 其中蓝色和黑色虚线分别标记近场和远场信源的入射方向。特别地, 对MVDR方法而言, 由于其导向矢量的计算涉及协方差矩阵的取逆操作, 而经投影后的协方差矩阵{{\boldsymbol{R}}_{\rm{P}}} (见式(19))将是秩亏缺的, 为使计算可行, 此处采用对角加载后的{\widetilde {\boldsymbol{R}}_{\rm{P}}} = {{\boldsymbol{R}}_{\rm{P}}} + \gamma{\boldsymbol{ I}} 以代替{{\boldsymbol{R}}_{\rm{P}}} 进行求逆, 对角加载因子\gamma 被设定为\gamma = 0.001 \times {\rm{trace}}\left\{ {{{\boldsymbol{R}}_{\rm{P}}}} \right\} , 此处{\rm{trace}}\left\{ \cdot \right\} 为矩阵取迹操作; 此外, MVDR方法中的导向向量也将按照左乘投影矩阵{\boldsymbol{P}}_{{{\boldsymbol{A}}_1}}^ \bot 的方式进行构建。图7(a)中未对混合信源进行空域分离, 该图表明, CBF对远场目标能够提供较为精确的测向结果, 但对近场信源入射方向的估计存在明显偏差, 这种偏差是由信号模型失配引入的系统误差所造成, 因此对该CBF谱解卷积依然无法解决上述问题。虽然R-L算法有效抑制了旁瓣且降低了主瓣束宽, 但由于默认所有信源均为远场分布, 因此为解释蓝色虚线附近的CBF主瓣, R-L算法依旧在相应位置建立了冲击形式的目标函数, 但所得结果与真实值相差较大。MVDR虽然有效抑制了近场信源所产生的虚影, 但依然存在较为明显的伪峰, 且对近场信源的角度估计结果偏离真实值。图7(b)中, 在通过正交投影操作隔离协方差矩阵的近场分量后, 所得CBF输出只保留了对应远场分量的波束, 有效消除了图7(a)中的歧义谱峰。随后进行一维反卷积求解, 所得波束图主瓣更窄且背景噪声级更低, 可以在不受近场源的干扰下有效探测远场目标。而MVDR算法虽然也通过正交投影操作消除了近场伪目标, 但却显现出较高的背景噪声级。
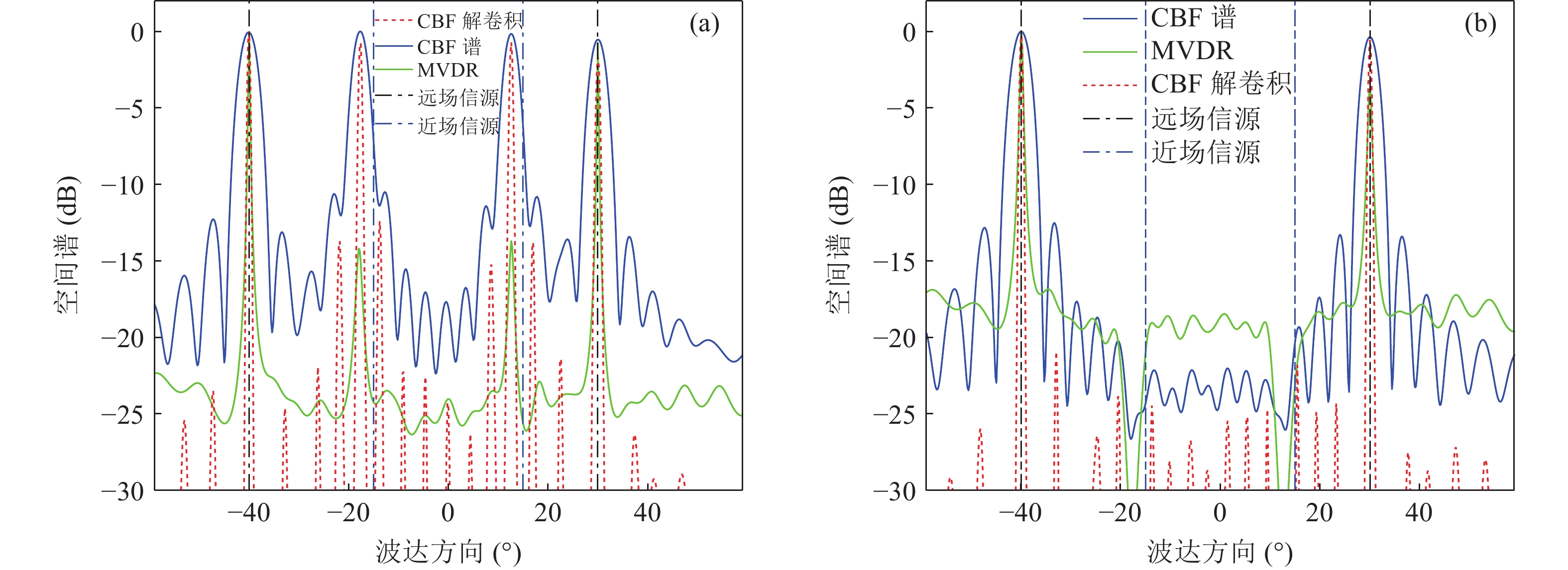
与图7(a)中的传统远场波束解卷积算法相比, 所提方法在图7(b)中的性能提升源自对近场信源的准确定位与有效隔离。然而, 在实际应用中, 旁瓣问题是普遍存在的(如图6(e)和图6(f)所示), 如在利用功率阈值法进行信源数估计时, 有时不可避免地将一些较强的旁瓣视为信号而保留(对应阈值较低情形), 这将导致额外的近场虚源被引入; 或将一些较弱的信号视为旁瓣而排除(对应阈值较高情形), 则将导致近场真实目标的遗漏。这种误判对算法远场测向的影响需要被进一步分析。设近场、远场信源入射方向集合分别为
{\varTheta _1} 和{\varTheta _2} , 由于各个信号波达方向不同, 需满足{\varTheta _1} \cap {\varTheta _2} = \emptyset , 再设由旁瓣所引入的近场虚源所处角度为{\varTheta _3} 。当一些真实近场目标被遗漏, 这表明被遗漏的目标强度必然非常微弱, 即使没有通过构造正交投影算子对其进行隔离, 它们对远场测向带来的影响也会十分有限; 当一些额外的虚源被引入, 如果{\varTheta _3} 和{\varTheta _2} 之间存在非空交集\varTheta ' , 则当构造{\varTheta _3} 的正交投影矩阵时, 位于\varTheta ' 处的远场信源会被一并排除, 导致它们在随后的远场测向步骤中无法被感知; 如果{\varTheta _3} \cap {\varTheta _2} = \emptyset , 即\left\{ {{\varTheta _1},{\varTheta _3}} \right\} \cap {\varTheta _2} = \emptyset , 则即使隔离方向\left\{ {{\varTheta _1},{\varTheta _3}} \right\} 上的信号分量, 原则上也不会对位于{\varTheta _2} 处的远场信源测向带来影响。当然, 实际应用中也可能会出现远近场信号入射方向虽不同但相近的情况。此时算法的性能依然会受到负面影响, 这是因为: (1) 当远近场混合源角度间隔较近时, 此时二者的空域特性相似(对应的导向矢量差别较小), CBF会存在性能下降问题, 如空间谱大范围模糊、波束主极大偏离目标方位等, 解卷积算法虽能在一定程度上对上述情况做出改善, 但能力有限, CBF性能的严重下降会对后续的解卷积操作造成不可逆的负面效应; (2) 在构造近场信源的正交投影算子时, 该步骤也会对远场临近源产生影响, 削弱其空域能量分布, 导致在远场测向时算法可能无法对它们做出正确响应。3.3 存在阵列误差下的定位性能
本组仿真评估阵列误差存在时所提算法的性能表现, 重点考虑阵型失配问题, 它可能由阵列的非理想布放、外力扰动等因素引起。首先, 基于以上仿真参数, 与基于子空间理论的LOFNS算法相对比, 50次独立的随机实验结果在图8中给出。可以发现, 不存在阵列误差时, 两算法均能给出准确的远场定位结果, 但对近场目标, 本文所提出的解卷积算法可提供更为精确的角度−距离估计。
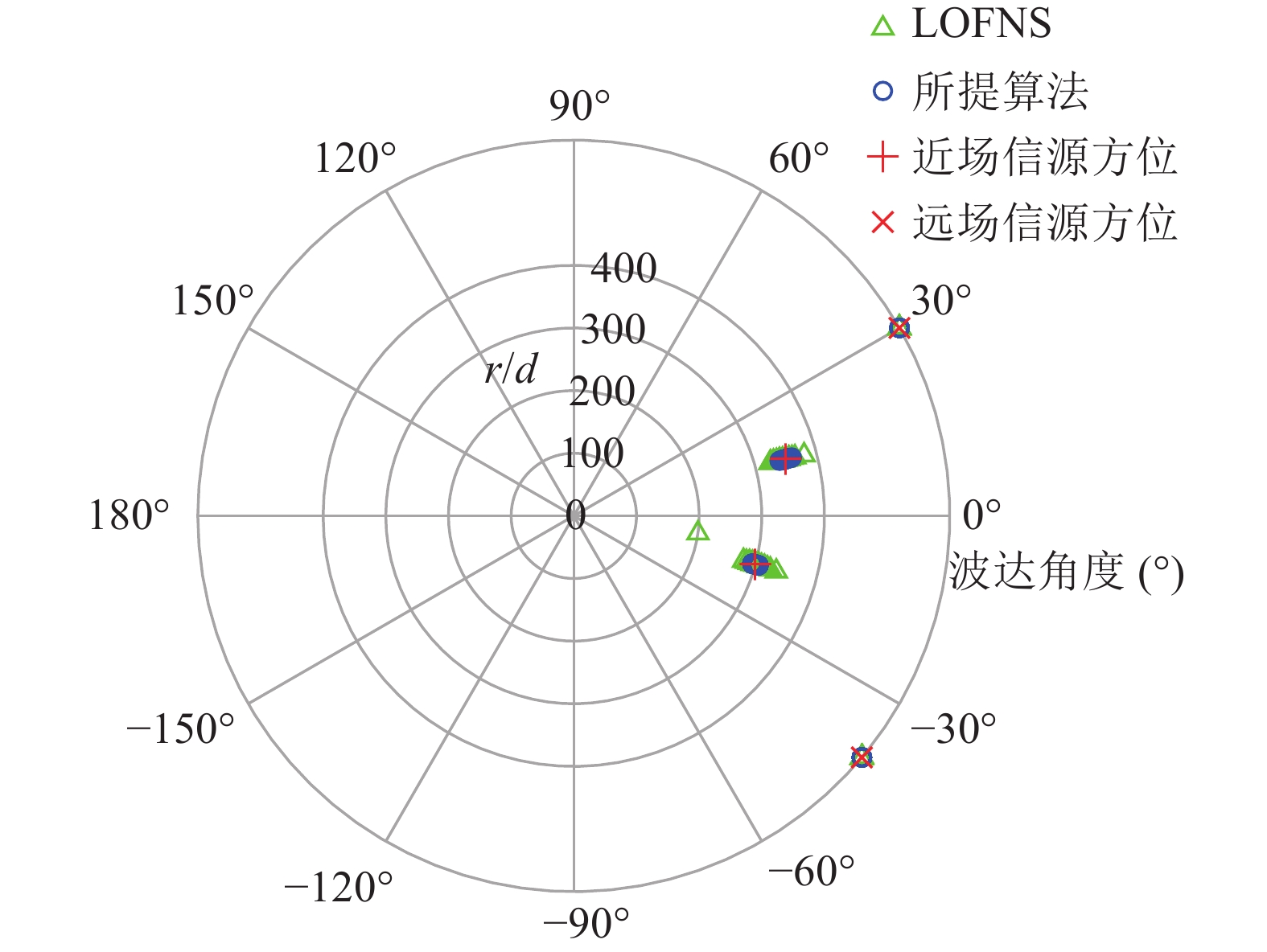
随后, 考虑阵列的一维扰动模型, 如图9所示, 其中传感器的理想位置和被扰动后的实际位置分别由蓝色圆圈和红色叉号给出, 相应的50次估计结果绘制于图10中。由图可知, 当阵列误差存在时, LOFNS算法对近场目标的估计偏差明显增大。相比之下, 解卷积算法虽然对近场信源的定位精度略有下降, 但依然可以得出可靠的估计结果, 显示出了对阵列误差更强的鲁棒性。这一性能优势可解释如下: LOFNS算法基于子空间理论, 对阵列失配较为敏感, 当阵元偏离预期位置, 相应的阵列流形将被扰动, 导致估计出的噪声子空间不再与理想导向矢量正交, 从而使得算法性能发生显著下降。而基于CBF的解卷积算法一定程度上继承了CBF鲁棒性强的优点, 这已在本组仿真中得到验证。
3.4 近场强干扰下的远场目标探测
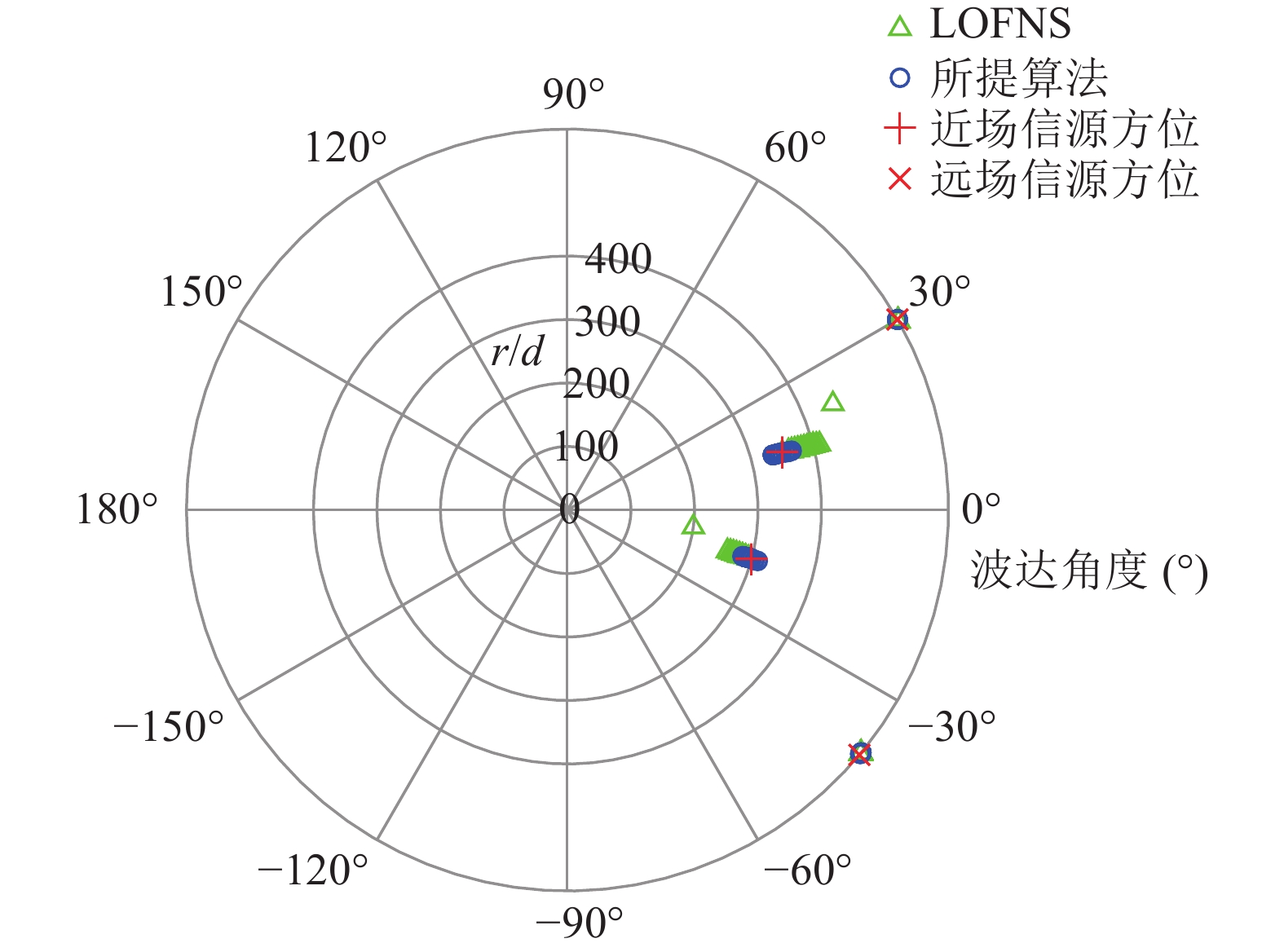
仿真条件2: 单个近场信源入射角度为
{\theta _1} = 20^\circ , 距离为{r_1} = {\text{450}}d , 单个远场信源入射角度为{\theta _2} = 0^\circ , 远场、近场目标信噪比设定为0 dB和20 dB, 其余仿真参数同上。本组仿真目的在于测试存在近场强干扰时各种算法对远场弱目标的探测性能。首先, 绘制近场区域CBF空间谱得到图11(a), 其中
\Delta \theta = {5^\circ },\;\Delta r = 10d 。由于近场目标能量较高, 因此CBF解卷积后(对应图11(b))对近场信源给出了较为精确的估计结果, 但应注意, 此时远场弱目标的主瓣已被近场信源的旁瓣所掩盖, 即使经过解卷积处理, 仍未能探测到远场信源。但依据所得结果依然可以重构近场流形并通过投影操作以尽可能消除其影响, 据此得到远场一维估计结果, 见图12。其中, 图12(a)直接基于协方差矩阵(未抑制近场干扰)对信源进行测向, CBF方法对近场强目标敏感, 但估计结果偏离真实方向, 且没有对真正的远场信源做出响应, 因此后续的解卷积操作(迭代50次)所得结果依然不尽人意。MVDR波束形成可给出精确的远场方位估计, 但依然无法屏蔽近场信源的干扰, 对其的估计结果偏离真实值。图12(b)结果印证了投影操作的有效性, 此时CBF算法能够探测到远场弱目标, 而相应的解卷积波束主瓣更窄, 增强了空域分辨能力, 而且有效抑制了波束旁瓣(约5~10 dB)。对比左右两图, 远场目标的成功探测归因于对距离信息的充分利用, 近场、远场目标所对应的r 值不同这一条件被图11中的粗解卷积操作充分捕捉并被利用, 因此可根据解卷积后的空间谱实现远近场混合源的空域分离, 移除近场强干扰后, 对远场信源的探测变得更为容易。此外, 将所得结果与图11(b)相对比可以发现, 图11(b)中被忽略的远场目标在图12(b)中被成功探测到, 这反映了组合式策略的优势: 将远场、近场波束解卷积算法合理结合有效解决了单个算法难以完成的任务, 因此适用范围更广, 对某些复杂情况的处理也更为灵活、有效。4. 结论
本文基于线列阵对远近场混合源的观测结果, 推导了其CBF谱中固有的二维卷积数学特性, 给出了一种组合式波束解卷积的混合源定位算法, 进而松弛了传统波束解卷积方法对单一近场/远场信源模型的刚性依赖, 此外还推导了协方差矩阵经近场流形正交投影操作后关于角度参数的远场一维卷积模型, 后使用Richardson–Lucy算法实现解卷积操作。数值仿真分析表明: (1) 所提算法可实现对混合源的空域分离, 并在提高了空域分辨力的同时降低了背景噪声级, 因此增强了对远场、近场信号的分辨能力与定位精度; (2) 相较于子空间定位方法, 本文方法对阵元位置失配具有宽容性; (3) 所提方法能够在抑制近场干扰的情况下给出远场信源的准确波达估计。
-
-
[1] Capon J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE, 1969; 57(8): 1408—1418 DOI: 10.1109/PROC.1969.7278
[2] Schmidt R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag., 1986; 34(3): 276—280 DOI: 10.1109/TAP.1986.1143830
[3] 孙爽, 乔渭阳, 黄晓聃. 传声器阵列反卷积法在飞机噪声测试中的应用. 噪声与振动控制, 2009; 29(5): 121—125 DOI: 10.3969/j.issn.1006-1355.2009.05.032 [4] 王朋, 迟骋, 纪永强, 等. 二维解卷积波束形成水下高分辨三维声成像. 声学学报, 2019; 44(4): 613—625 DOI: 10.15949/j.cnki.0371-0025.2019.04.022 [5] Zhou T, Huang J, Du W, et al. 2-D deconvolved conventional beamforming for a planar array. Circuits Syst. Signal Process., 2021; 40(11): 5572—5593 DOI: 10.1007/s00034-021-01733-6
[6] Sun D, Ma C, Yang T C, et al. Improving the performance of a vector sensor line array by deconvolution. IEEE J. Oceanic Eng., 2020; 45(3): 1063—1077 DOI: 10.1109/JOE.2019.2912586
[7] 谢磊, 孙超, 刘雄厚, 等. 解卷积的多重信号分类算法方位谱低背景处理方法. 声学学报, 2018; 43(4): 516—525 DOI: 10.15949/j.cnki.0371-0025.2018.04.011 [8] 石文佩. 基于反卷积的近场声源稳健高分辨被动定位方法. 硕士学位论文, 哈尔滨: 哈尔滨工程大学, 2019 [9] Yang T C. Deconvolved conventional beamforming for a horizontal line array. IEEE J. Oceanic Eng., 2018; 43(1): 160—172 DOI: 10.1109/JOE.2017.2680818
[10] Yang T C. Performance analysis of superdirectivity of circular arrays and implications for sonar systems. IEEE J. Oceanic Eng., 2019; 44(1): 156—166 DOI: 10.1109/JOE.2018.2801144
[11] Lucy L B. An iterative technique for the rectification of observed distributions. Astron. J., 1974; 79: 745—754 DOI: 10.1086/111605
[12] Richardson W H. Bayesian-based iterative method of image restoration. J. Opt. Soc. Am., 1972; 62(1): 55—59 DOI: 10.1364/JOSA.62.000055
[13] Ma C, Sun D, Mei J, et al. Spatiotemporal two-dimensional deconvolution beam imaging technology. Appl. Acoust., 2021; 183: 108310 DOI: 10.1016/j.apacoust.2021.108310
[14] 马超. 空域移变反卷积波束形成方法研究. 博士学位论文, 哈尔滨: 哈尔滨工程大学, 2021 [15] 梅继丹, 石文佩, 马超, 等. 近场反卷积聚焦波束形成声图测量. 声学学报, 2020; 45(1): 15—28 DOI: 10.15949/j.cnki.0371-0025.2020.01.002 [16] Mei J, Pei Y, Zakharov Y, et al. Improved underwater acoustic imaging with non-uniform spatial resampling RL deconvolution. IET Radar Sonar Navig., 2020; 14(11): 1697—1707 DOI: 10.1049/iet-rsn.2020.0175
[17] Sun D, Ma C, Mei J, et al. Improving the resolution of underwater acoustic image measurement by deconvolution. Appl. Acoust., 2020; 165: 107292 DOI: 10.1016/j.apacoust.2020.107292
[18] He J, Li L, Shu T, et al. Mixed near-field and far-field source localization based on exact spatial propagation geometry. IEEE Trans. Veh. Technol., 2021; 70(4): 3540—3551 DOI: 10.1109/TVT.2021.3065954
[19] Liang J, Liu D. Passive localization of mixed near-field and far-field sources using two-stage MUSIC algorithm. IEEE Trans. Signal Process., 2010; 58(1): 108—120 DOI: 10.1109/TSP.2009.2029723
[20] Zuo W, Xin J, Zheng N, et al. Subspace-based localization of far-field and near-field signals without eigendecomposition. IEEE Trans. Signal Process., 2018; 66(17): 4461—4476 DOI: 10.1109/TSP.2018.2853124
[21] 邱龙皓, 梁国龙, 王燕, 等. 稀疏贝叶斯学习远近场混合源定位方法. 声学学报, 2018; 43(1): 1—11 DOI: 10.15949/j.cnki.0371-0025.2018.01.001 [22] 母采凤, 李森, 吕梦然. 脉冲噪声环境下基于矩阵差分的远近场混合源定位. 信号处理, 2022; 38(11): 2342—2349 DOI: 10.16798/j.issn.1003-0530.2022.11.011 [23] He J, Shu T, Li L, et al. Mixed near-field and far-field localization and array calibration with partly calibrated arrays. IEEE Trans. Signal Process., 2022; 70: 2105—2118 DOI: 10.1109/TSP.2022.3168975
[24] He J, Swamy M N S, Ahmad M O. Efficient application of MUSIC algorithm under the coexistence of far-field and near-field sources. IEEE Trans. Signal Process., 2012; 60(4): 2066—2070 DOI: 10.1109/TSP.2011.2180902
[25] Chu Z, Yang Y, He Y. Deconvolution for three-dimensional acoustic source identification based on spherical harmonics beamforming. J. Sound Vib., 2015; 344: 484—502 DOI: 10.1016/j.jsv.2015.01.047
-
期刊类型引用(1)
1. 孙大军,黄天凤,梅继丹,崔文婷. 极坐标系快速反卷积高分辨声图测量方法. 声学学报. 2024(05): 967-978 .  本站查看
本站查看
其他类型引用(2)



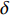
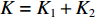
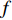



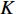
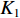
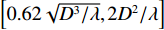
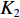





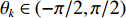
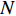
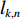

 下载:
下载: