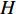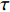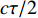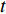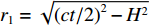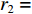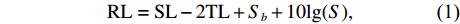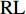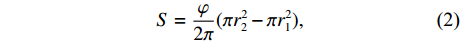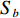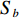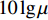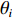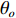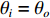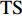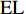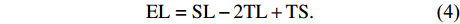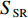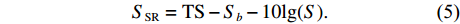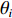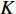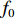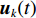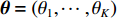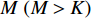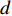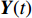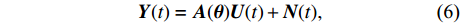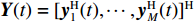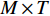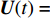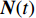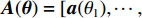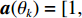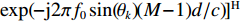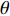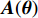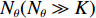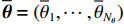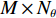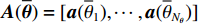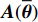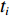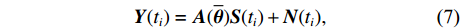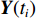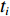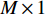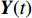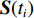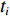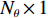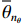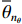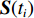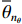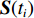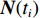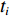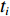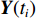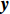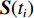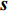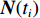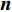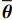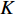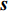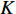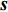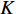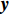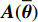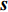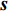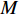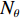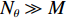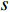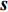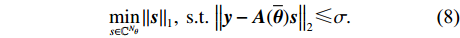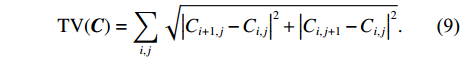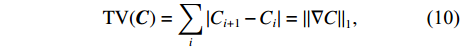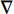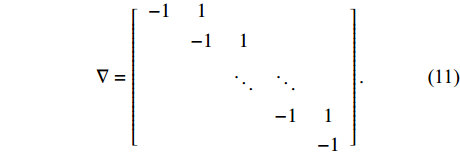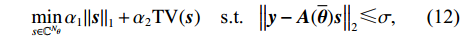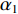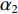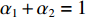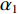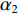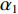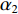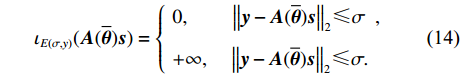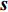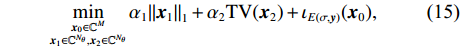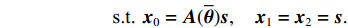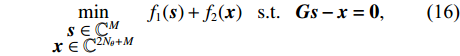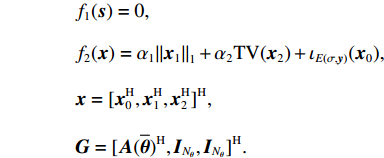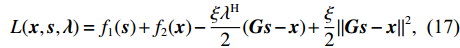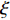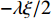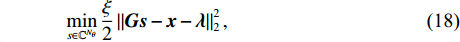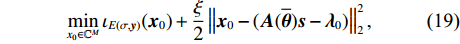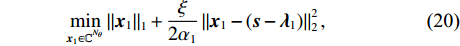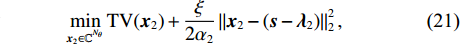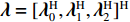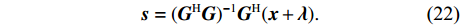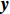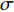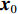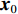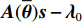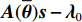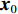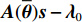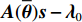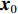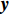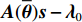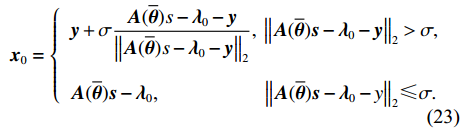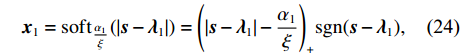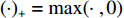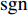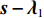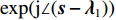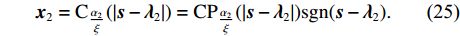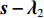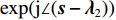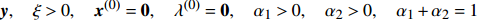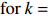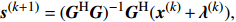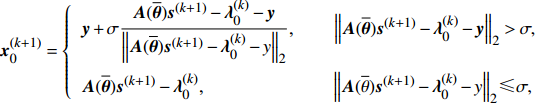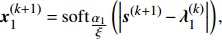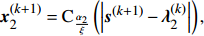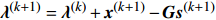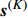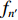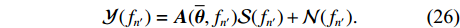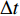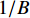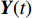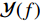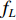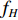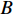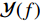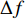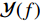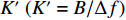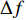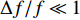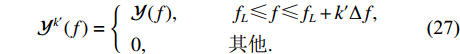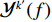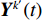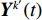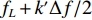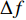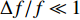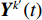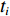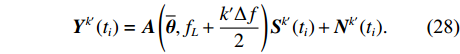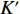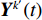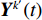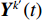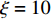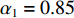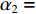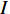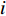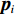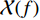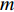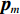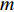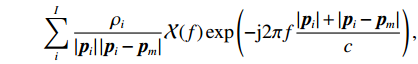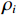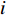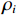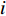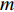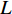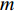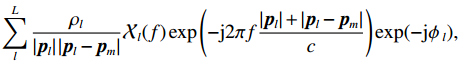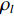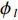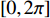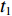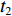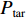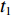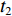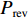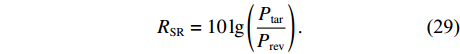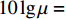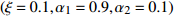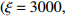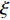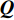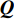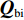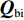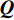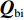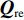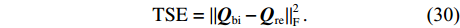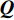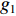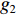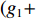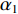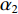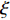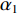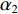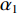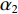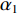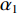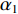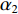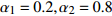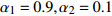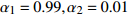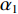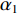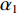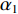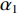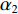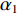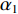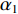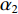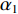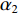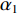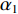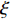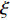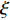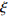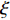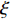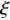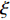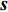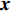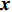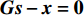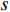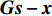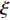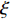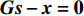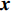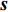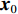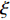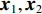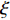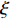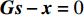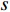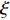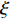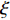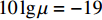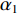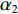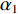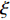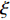Seabed target detection under the constraint of mixed 1-norm and total variation
-
摘要:
提出了一种以1范数与全变分的加权和作为正则项的方位估计算法, 该算法通过1范数稀疏约束来获得高分辨能力, 采用全变分约束来加强目标边缘特征并提高其内部的平滑性, 在提高方位分辨率的同时, 改善了对方位扩展目标估计性能。在宽带条件下对算法进行了扩展, 将接收信号在频域分频后的子频带变换回时域, 再在时域上使用窄带算法进行处理, 这样避免了时域分段处理造成的时间分辨力的损失。结合了海底探测场景进行了仿真实验验证, 结果显示, 所提算法的探测结果不仅获得了方位分辨率提升, 而且总平方误差小于目前常见的同类算法。因此, 在对海底大型方位扩展目标的探测当中, 通过在稀疏优化类方位估计方法中加入全变分约束能够保持目标的结构特征, 有效提升探测性能。
Abstract:This paper presents an innovative sparse-constrained arrival estimation algorithm using a weighted sum of the 1-norm and total variation constraints as a regularization term. The proposed algorithm achieves high resolution under the 1-norm sparsity constraint and enhances the target's edge features and internal smoothness under the total variation constraint. In addition, the proposed algorithm can improve both the direction of arrival resolution and the estimation performance of the direction of arrival extended targets. Further, the proposed algorithm is extended to the broadband scenes, where the received signal is transformed back to the time domain after being divided into sub-bands in the frequency domain. The obtained time-domain signals are processed by narrowband algorithms. The main advantage of the proposed method is that it avoids the loss of range resolution caused by conventional piecewise processing. The effectiveness of the proposed algorithm is verified by simulation experiments in a seabed exploration scenario. The experimental results show that the proposed algorithm not only can enhance the azimuth resolution but can also reduce the total square error compared to the commonly-used algorithms. Finally, the results demonstrate that adding the total variation constraints to the sparse-constrained direction of the arrival estimation algorithm can preserve the structural properties of targets and effectively improve the detection performance of large azimuth-expanding targets on the seabed.
-
引言
在海底目标探测当中, 由发射声波在海底界面上的散射形成的海底混响[1]为主要背景干扰, 其强度的大小受到多种因素的影响, 大量的测量数据表明[2-4], 对于同样的海底底质类型, 海底散射强度大小与声波掠射角呈正相关。为了定量描述这种关系, 学者们提出了多种海底散射模型[4-6], 其中兰伯特散射模型简易方便, 且在掠射角小于45°时能够较好地拟合实验数据[3-4]。基于海底散射强度随掠射角减小而降低这一特性, 可以通过降低设备的工作高度, 使目标探测区域处于较小的掠射角下, 降低海底混响, 提高信混比(SRR), 从而保证探测算法的性能。
海底探测的精度主要取决于两个方面, 方位向分辨能力与时间向分辨能力。由于受到阵列物理孔径的限制, 常规波束形成(CBF)[7]的方位分辨能力较低。Capon通过无失真约束使波束输出噪声最小, 提出了一种自适应的方位估计方法, 提高了方位分辨能力[8]。Schmidt等基于信号子空间与噪声子空间的正交性, 提出了多重子空间分类法, 突破了瑞利限, 实现了超分辨[9]。Yang等通过解卷积算法消除点扩散函数的影响, 从而提高了均匀直线阵对点目标的分辨能力[10]。王朋等对三维成像声呐的结果进行二维解卷积处理, 得到了分辨率更高, 旁瓣更低的成像结果[11]。稀疏优化类的算法, 利用点目标稀疏的先验条件, 通过1范数对解的稀疏性进行约束, 得到了更加优秀的分辨能力[12], 且可以应用于单快拍的条件下。全变分(TV)[13]最早是由Rudin提出的一种图像去噪模型, 它能够使图像中目标更加平滑, 并提高其边缘特征。Güven等将全变分与1范数相结合作为正则项, 利用稀疏恢复模型进行雷达成像[14], 王硕等将其应用在窄带水下三维声成像当中, 取得了较好的成像结果[15], 但并没有将其扩展至宽带情况下。
为了同时能够获得时间向的高分辨能力, 需要使用宽带信号。宽带信号的处理, 传统通常采取以下方式, 对于常规波束形成, 可以直接在频域波束形成后再反变换回时域, 得到方位时间强度图像[16]; 而稀疏优化类方位估计算法一般采用在时域进行分段, 对分段信号采用频域快拍处理[12], 得到该段信号的一个估计结果, 再将各个分段信号的方位估计结果按照时间进行排列, 得到目标区域的方位时间强度探测结果。
上述探测方法中, 在方位向上, 多基于点目标假设, 而实际上海底残骸目标一般是具有一定外形的方位扩展目标, 使用基于点目标假设的高分辨方位估计算法对方位扩展目标进行估计会导致估计结果离散成为多个孤立亮点, 产生失真; 而在时间向上, 针对宽带信号所采取的时域分段处理方法中, 信号分段长度一般会大于宽带信号的时间分辨率, 从而造成探测结果时间分辨率的损失。本文通过在传统1范数稀疏优化的方位估计算法中引入全变分约束来改善算法对方位扩展目标的估计性能, 同时提出了通过FFT对宽带信号在频域分频后, 将子频带反变换回时域, 再对其按照窄带时域下约束分裂增广拉格朗日收缩迭代算法(CSALSA)进行求解[17], 最后对不同频率处理结果进行综合的处理方法, 避免了传统分段处理对时间向分辨能力的损失。通过仿真实验验证, 本文所提的方法获得方位分辨率提升的同时保持了目标的结构特征, 且目标内部平滑性提升, 探测结果的总均方误差小于传统算法, 在对方位扩展目标的探测上具有更高的实际应用价值。
1. 模型建立
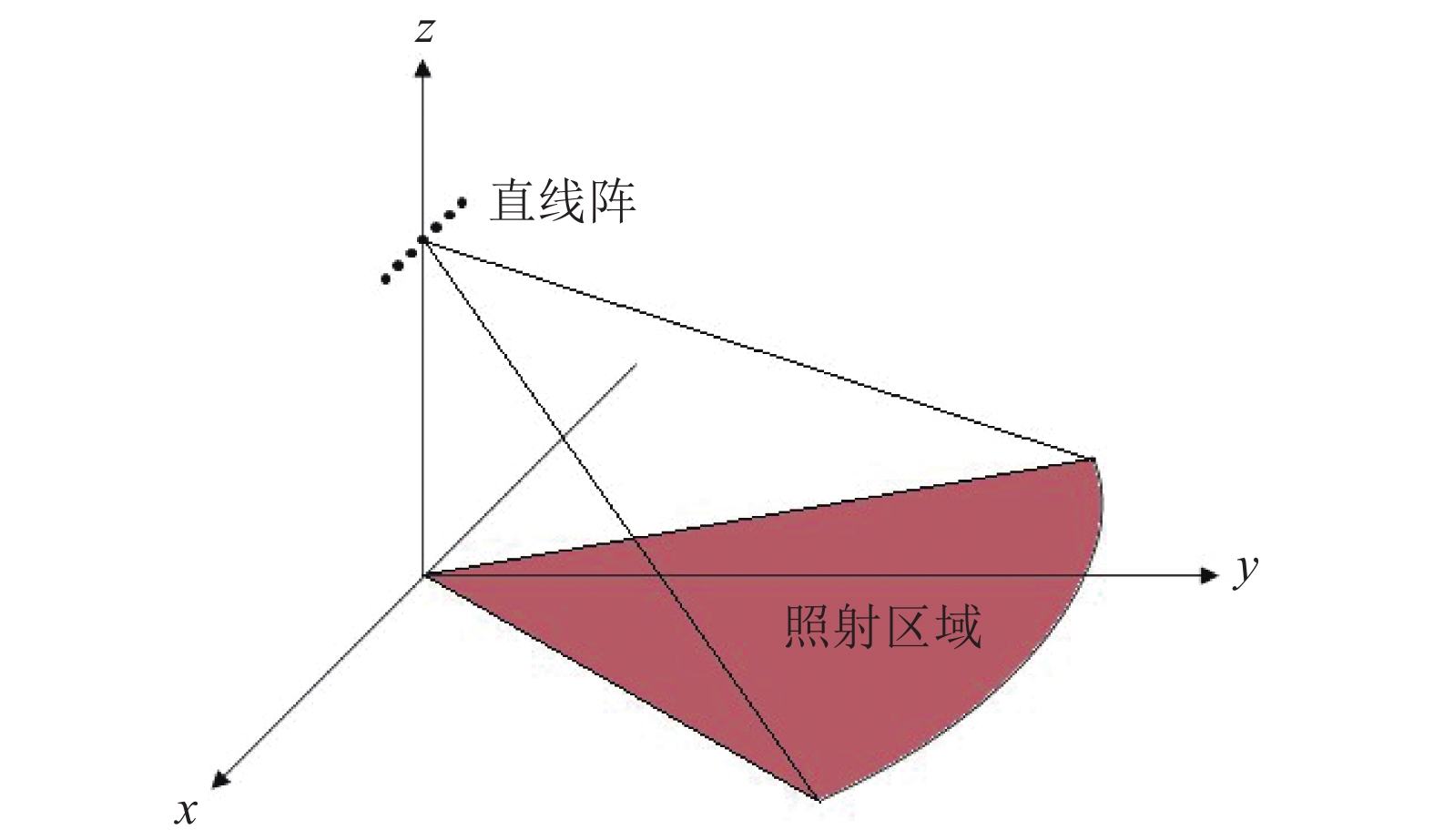
考虑图1所示探测模型, 采用指向性发射, 激励开角为
φ 的扇形海底区域。接收阵列为与发射扇面中轴线垂直的直线阵, 布阵方式使用半波长均匀布阵。通过对接收回波的处理, 得到目标区域的方位时间强度探测结果。现对模型做出一般性假设: (1) 声波沿直线传播, 且考虑球面波衰减; (2) 海底相对平坦, 散射体的数量足够大且其分布是随机均匀的; (3) 只考虑声波的一次散射, 不考虑多次散射回波。设工作高度为
H , 当声波由发射换能器发射后, 以球面波向外扩展, 对于脉冲宽度为τ 的发射脉冲, 声波覆盖区域实际上为厚度为cτ/2 的球壳。所以, 在某一时刻t , 对混响产生贡献的区域为球壳与海底界面相交的部分圆环, 圆环内径r1=√(ct/2)2−H2 , 圆环外径r2=√(c(t+τ)/2)2−H2 。根据有源声呐方程, 阵元接收到的海底混响混响级的大小为RL=SL−2TL+Sb+10lg(S), (1) 式中,
RL 是声源级,TL 是传播损失,S 是在一个脉冲长度内对混响有贡献的海底散射区域的面积, 对于t 时刻,S 的表达式如下:S=φ2π(πr22−πr21), (2) 而
Sb 是海底反向散射强度, 根据兰伯特散射定律[3-4],Sb 的表达式如下:Sb=10lgμ+10lg(sinθisinθo), (3) 其中,
10lgμ 为垂直入射时的散射强度, 该值与海底底质类型相关, 对于同一底质的海底, 该值为常数;θi 为声波入射角,θo 为声波散射角, 对于收发合置声呐来说, 存在θi=θo 。同样, 对于目标强度为
TS 的海底目标, 阵元接收到的目标回波信号级EL 为EL=SL−2TL+TS. (4) SSR=TS−Sb−10lg(S). (5) 从上述推导结果可以看出, 当发射脉宽一定的情况下, 阵元接收信混比的主要影响因素为声波的掠射角
θi , 掠射角越小, 海底混响强度就越小, 接收信号信混比就越大。2. 算法描述
2.1 混合1范数与全变分正则化优化模型
考虑
K 个频率为f0 的远场窄带平面波{{\boldsymbol{u}}_k}(t) 以入射角{\boldsymbol{\theta}} = ({\theta _1}, \cdots ,{\theta _K}) 入射到一个由M{\text{ }}(M > K) 个阵元组成的均匀直线阵上, 阵元间距d 等于半波长。则阵列接收数据矩阵{\boldsymbol{Y}}(t) 可以写作如下形式 :{\boldsymbol{Y}}(t) = {\boldsymbol{A}}({\boldsymbol{\theta}} ){\boldsymbol{U}}(t) + {\boldsymbol{N}}(t), (6) 式中,
{\boldsymbol{Y}}(t) = {[{\boldsymbol{y}}_1^{\rm{H}}(t), \cdots ,{\boldsymbol{y}}_M^{\rm{H}}(t)]^{\rm{H}}} 为M \times T 维矩阵;{\boldsymbol{U}}(t) = {[{\boldsymbol{u}}_1^{\rm{H}}(t), \cdots ,{\boldsymbol{u}}_K^{\rm{H}}(t)]^{\rm{H}}} 为入射信号矩阵, 其维度为K \times T ;{\boldsymbol{N}}(t) 为M \times T 维的加性白噪声; 而{\boldsymbol{A}}({\boldsymbol{\theta}} ) = [{\boldsymbol{a}}({\theta _1}), \cdots , {\boldsymbol{a}}({\theta _K})] 为M \times K 维的阵列方向矩阵, 其中{\boldsymbol{a}}({\theta _k}) = [1, {\rm{exp}}( - {\rm{j}}2\pi {f_0}\sin( {\theta _k})d/c ), \cdots ,{\rm{exp}}( - {\rm{j}}2\pi {f_0}\sin( {\theta _k}) (M - 1)d/c) ]^{\rm{H}} 。在该模型中,\theta 是未知的, 因此{\boldsymbol{A}}({\boldsymbol{\theta}} ) 也是未知的。对上述阵列接收信号模型进行稀疏表示。将目标区域进行等间隔划分为
{N_\theta }({N_\theta } \gg K) 个可能来波角度, 记作\overline {\boldsymbol{\theta}} = ({\overline \theta _1}, \cdots ,{\overline \theta _{{N_\theta }}}) 。定义M \times {N_\theta } 维的过完备基矩阵{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ) = [{\boldsymbol{a}}({\overline \theta _1}), \cdots ,{\boldsymbol{a}}({\overline \theta _{{N_\theta }}})] , 其每一列代表对应划分角度上的方向向量, 因此这里的{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ) 是已知量。考虑取某一固定时刻{t_i} , 得到的稀疏信号模型表达式如下:{\boldsymbol{Y}}({t_i}) = {\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{S}}({t_i}) + {\boldsymbol{N}}({t_i}), (7) 式中,
{\boldsymbol{Y}}({t_i}) 为{t_i} 时刻的M \times 1 维的单快拍阵列接收信号, 代表{\boldsymbol{Y}}(t) 的一列;{\boldsymbol{S}}({t_i}) 为{t_i} 时刻的{{{N}}_\theta } \times 1 维的稀疏信号, 其每个元素均对应一个划分角度{\overline \theta _{{n_\theta }}} , 当{\overline \theta _{{n_\theta }}} 方向不存在来波时, 则{\boldsymbol{S}}({t_i}) 中对应元素为0, 反之, 若{\overline \theta _{{n_\theta }}} 方向存在来波,{\boldsymbol{S}}({t_i}) 中对应元素不为0;{\boldsymbol{N}}({t_i}) 为{t_i} 时刻的噪声。在接下来的推导当中, 为了表达方便, 会忽略式(7)中的{t_i} , 并将{\boldsymbol{Y}}({t_i}) 记作{\boldsymbol{y}} ,{\boldsymbol{S}}({t_i}) 记作{\boldsymbol{s}} ,{\boldsymbol{N}}({t_i}) 记作{\boldsymbol{n}} 。由于真实来波方位相对于整个空间来说是稀疏的, 即划分角度\overline {\boldsymbol{\theta}} 当中只有K 个方向上存在来波。相应地,{\boldsymbol{s}} 的所有元素中, 只存在K 个非零元素, 即{\boldsymbol{s}} 为K 稀疏的。对于上述稀疏信号模型, 需要通过阵列接收数据
{\boldsymbol{y}} 与已知的过完备基矩阵{\boldsymbol{A}}(\overline{\boldsymbol{ \theta}} ) , 恢复出稀疏信号{\boldsymbol{s}} , 而{\boldsymbol{s}} 中的非零项对应的划分角度即为真实来波方向。再观察式(7)可以发现, 忽略噪声项, 一共存在M 个方程与{N_\theta } 个未知数, 由于一般存在{N_\theta } \gg M , 该问题是一个欠定问题, 存在无数多个解。为了求解上述欠定问题, 需要对s 施加稀疏性约束来缩小解空间。0范数能够很好地约束向量的稀疏性, 但是由于其优化求解是一个NP-Hard问题, 所以一般考虑使用1范数对稀疏性进行约束[18]。于是, 对{\boldsymbol{s}} 的求解变为了如下的优化问题:\mathop {\min }\limits_{s \in {\mathbb{C}^{{N_\theta }}}} {\left\| {\boldsymbol{s}} \right\|_1},~{\rm s.t.}~{\left\| {{\boldsymbol{y}} - {\boldsymbol{A}}(\overline{\boldsymbol{ \theta}} ){\boldsymbol{s}}} \right\|_2} \leqslant \sigma . (8) 然而对于图1海底探测场景来说, 式(8)所示优化模型存在着一定的缺陷, 即大型残骸目标是一种方位扩展目标, 其回波方位虽然在整个空间上是稀疏的, 但是在局部上, 则是连续的。1范数稀疏约束只考虑了目标在整个空间上的稀疏性, 没考虑方位扩展目标在局部上的连续性, 仅使用1范数作为正则项约束会使得到的解会过于稀疏, 从而造成失真。下面通过引入全变分约束来改善这一问题。
全变分最早被用于图像去噪与复原, 能够使图像中目标内部更加平滑的同时加强目标的边缘特征[13], 二维全变分的表达式如下所示:
{\rm{TV}}({\boldsymbol{C}}) = \sum\limits_{i,j} {\sqrt {{{\left| {{C_{i + 1,j}} - {C_{i,j}}} \right|}^2} + {{\left| {{C_{i,j + 1}} - {C_{i,j}}} \right|}^2}} .} (9) 在水声探测中, 对接收到的信号按照时间进行处理, 每次处理信号为一维信号, 所以将式(9)中的二维全变分降维成适合探测场景的一维全变分如下:
{\rm{TV}}({\boldsymbol{C}}) = \sum\limits_i {\left| {{C_{i + 1}} - {C_i}} \right| = {{\left\| {\nabla C} \right\|}_1}} , (10) 式中,
\nabla 代表差分算子, 其表达式如下:\nabla=\left[\begin{array}{ccccc} -1 & 1 & & & \\ & -1 & 1 & & \\ & & \ddots & \ddots & \\ & & & -1 & 1 \\ & & & & -1 \end{array}\right] . (11) 向量的一阶差分实际上代表着向量本身的平滑程度, 向量越平滑, 其一阶差分中非零值就越少, 而一阶差分中的非零值意味着原向量在此处发生了突变, 对应目标的边缘。从上面可以看出, 降维后的一维全变分实际上就是对向量的一阶差分进行1范数约束, 希望使一阶差分稀疏, 只在目标的边缘位置有值, 而目标连续存在的区域与没有目标的区域值为0, 从而达到提高目标边缘特征, 增加目标内部平滑性的目的。
通过引入一维全变分, 将其与1范数加权和作为正则项, 可以得到如下新的优化问题:
\mathop {\min }\limits_{s \in {\mathbb{C}^{{N_\theta }}}} {\alpha _1}{\left\| {\boldsymbol{s}} \right\|_1} + {\alpha _2}{\rm{TV}}({\boldsymbol{s}})~~~{\text{ s.t.}}~~~{\left\| {{\boldsymbol{y}} - {\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}}} \right\|_2} \leqslant \sigma , (12) 式中,
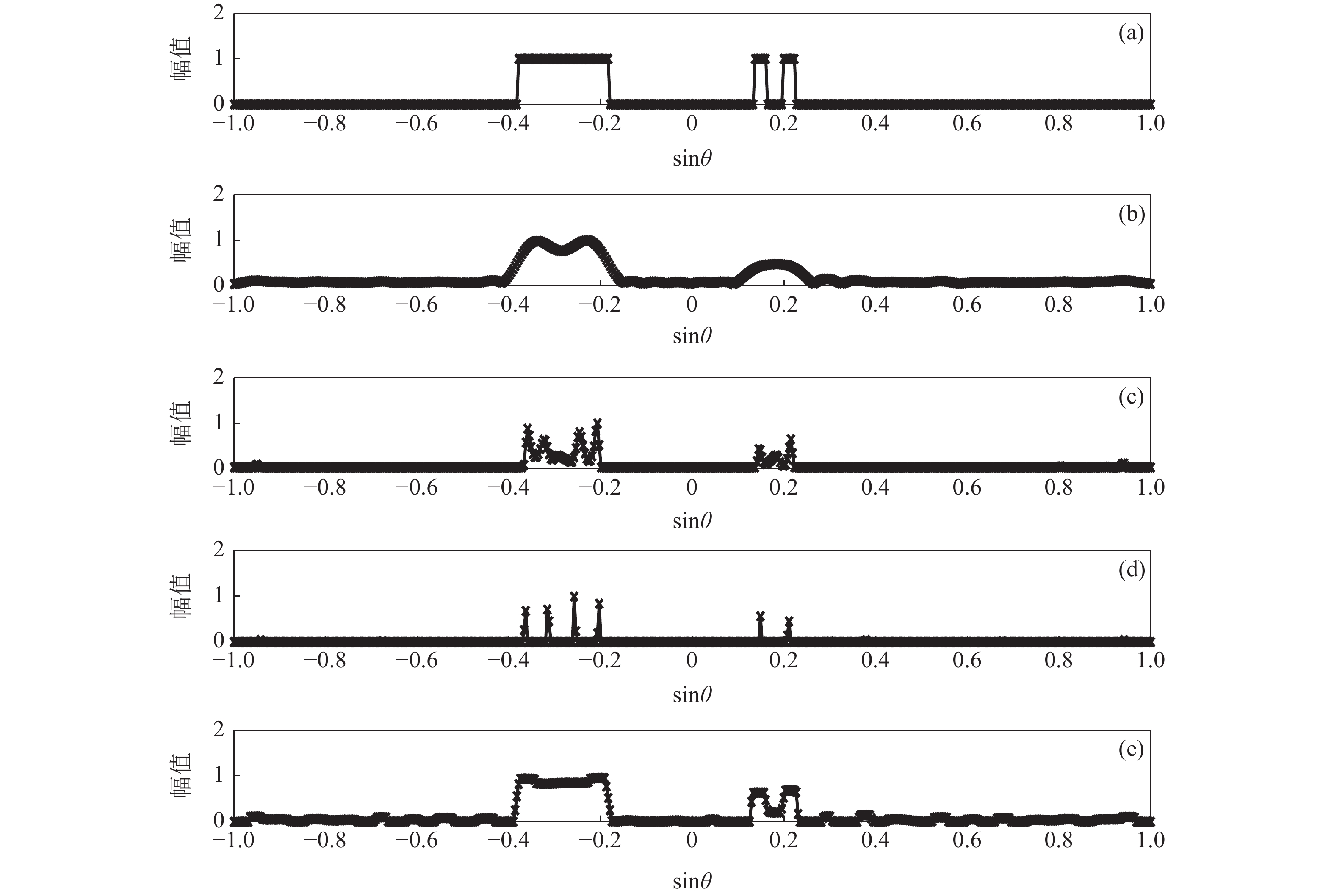
{\alpha _1} 与{\alpha _2} 为1范数与TV范数的权重, 且存在{\alpha _1} + {\alpha _2} = 1 , 提高{\alpha _1} 的值可以使解偏向于更加稀疏, 反之提高{\alpha _2} 则会使解偏向更加平滑, 可以针对不同的应用场景对{\alpha _1} 与{\alpha _2} 进行调节。2.2 分裂增广拉格朗日收缩迭代求解算法
上述优化问题是一个带不等式约束的优化问题, 对其进行求解之前, 通过变形并引入新变量将其转化为一个带等式约束的多变量优化问题。首先将式(12)中的不等式约束项作为惩罚项放入目标函数当中, 得到如下的无约束优化问题:
\mathop {\min }\limits_{{\boldsymbol{s}} \in {\mathbb{C}^{{N_\theta }}}} {\alpha _1}{\left\| {\boldsymbol{s}} \right\|_1} + {\alpha _2}{\rm{TV}}({\boldsymbol{s}}) + {\iota _{E(\sigma ,y)}}({\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}}), (13) 其中
{\iota _{E(\sigma ,y)}}({\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}}) = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {0,}&{{\text{ }}\quad{{\left\| {{\boldsymbol{y}} - {\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}}} \right\|}_2} \leqslant \sigma } \end{array},} \\ {\begin{array}{*{20}{l}} { + \infty ,}&\;{{{\left\| {{\boldsymbol{y}} - {\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}}} \right\|}_2} \leqslant \sigma .} \end{array}} \end{array}} \right. (14) 可以发现式(13)中的3项均为
{\boldsymbol{s}} 的函数, 直接对其进行求解较为困难。这里通过引入新变量对目标函数中3项的优化变量进行替换, 将其变换为下面带等式约束的优化问题:\mathop {\min }\limits_{\begin{subarray}{c} {{\boldsymbol{x}}_0} \in {\mathbb{C}^M} \\ {{\boldsymbol{x}}_1} \in {\mathbb{C}^{{N_\theta }}},{{\boldsymbol{x}}_2} \in {\mathbb{C}^{{N_\theta }}} \end{subarray} }{\alpha _1}{\left\| {{{\boldsymbol{x}}_1}} \right\|_1} + {\alpha _2}{\rm{TV}}({{\boldsymbol{x}}_2}) + {\iota _{E(\sigma ,{\boldsymbol{y}})}}({{\boldsymbol{x}}_0}), (15) {\text{s}}{\text{.t}}{\text{. }}{{\boldsymbol{x}}_0} = {\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}},{\text{ }} {\text{ }}\;\;{{\boldsymbol{x}}_1} = {{\boldsymbol{x}}_2} = {\boldsymbol{s}}. 进一步地, 可以将上式写成如下形式:
\mathop {\min }\limits_{\begin{array}{c} {\boldsymbol{s}} \in {\mathbb{C}^M} \\ {\boldsymbol{x}} \in {\mathbb{C}^{2{N_\theta } + M}} \end{array}} {f_1}({\boldsymbol{s}}) + {f_2}({\boldsymbol{x}})~~~{\rm s.t.}~~~{\boldsymbol{Gs}} - {\boldsymbol{x}} = {\boldsymbol{0}}, (16) 其中
\begin{split}& {f_1}({\boldsymbol{s}}) = 0, \\& {f_2}({\boldsymbol{x}}) = {\alpha _1}{\left\| {{{\boldsymbol{x}}_1}} \right\|_1} + {\alpha _2}{\rm{TV}}({{\boldsymbol{x}}_2}) + {\iota _{E(\sigma ,{\boldsymbol{y}})}}({{\boldsymbol{x}}_0}), \\& {\boldsymbol{x}} = {[{\boldsymbol{x}}_0^{\rm{H}},{\boldsymbol{x}}_1^{\rm{H}},{\boldsymbol{x}}_2^{\rm{H}}]^{\rm{H}}}, \\& {\boldsymbol{G}} = {[{\boldsymbol{A}}{(\overline {\boldsymbol{\theta}} )^{\rm{H}}},{{\boldsymbol{I}}_{{N_\theta }}},{{\boldsymbol{I}}_{{N_\theta }}}]^{\rm{H}}}. \end{split} 式(16)为带等式约束的多变量联合优化问题, 其增广拉格朗日函数如下:
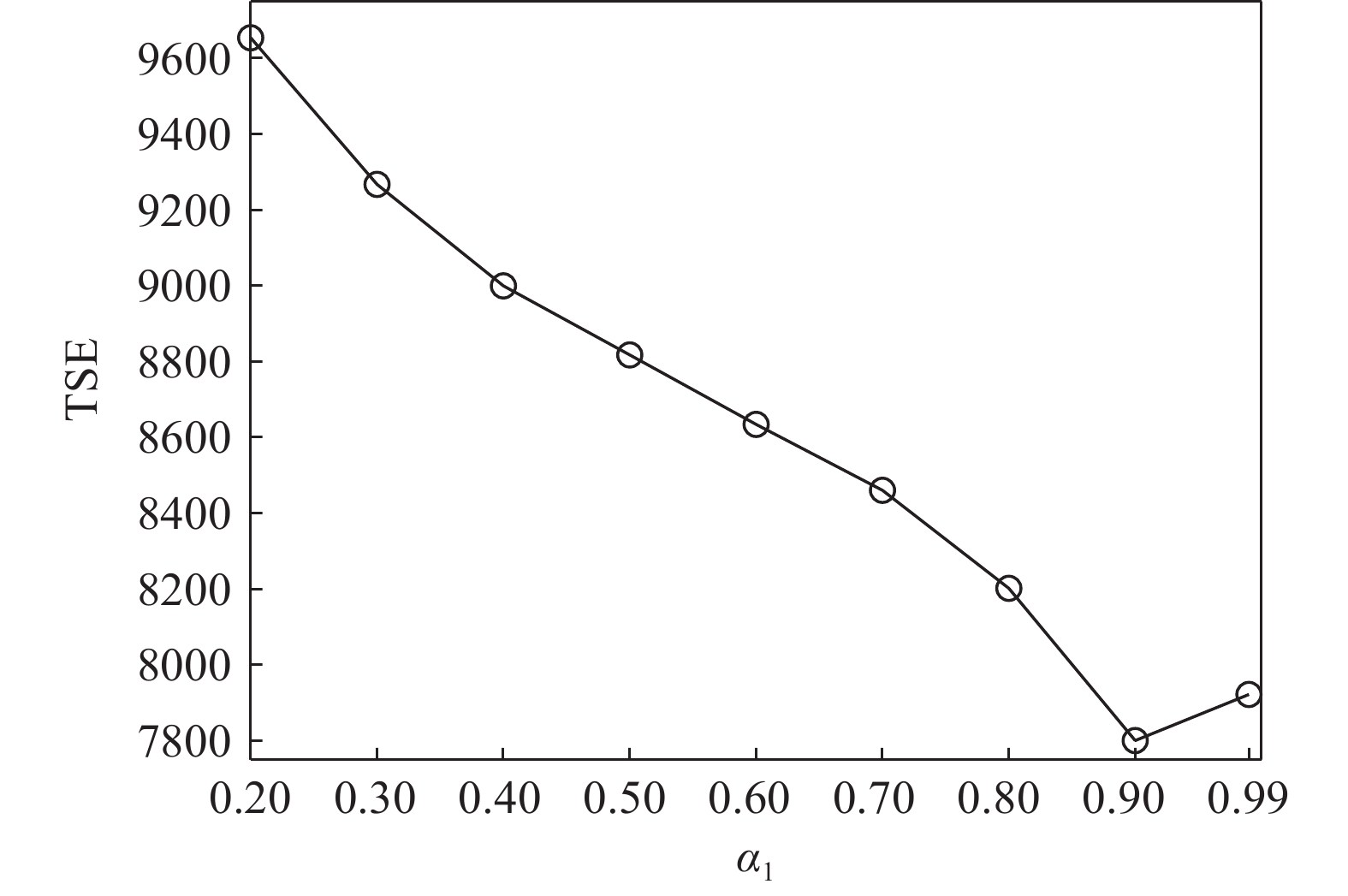
L({\boldsymbol{x}},{\boldsymbol{s}},{\boldsymbol{\lambda}} ) = {f_1}({\boldsymbol{s}}) + {f_2}({\boldsymbol{x}}) - \frac{{\xi {\lambda ^{\rm{H}}}}}{2}({\boldsymbol{Gs}} - {\boldsymbol{x}}) + \frac{\xi }{2}{\left\| {{\boldsymbol{Gs}} - {\boldsymbol{x}}} \right\|^2}, (17) 其中,
\xi 为惩罚因子, 是一常数, 为了后续推导的方便, 这里用- \lambda \xi /2 作为拉格朗日乘子, 对优化结果不产生影响。对式(17), 采用交替方向乘子法的思想, 交替对各个变量进行优化, 在对某个变量进行优化时, 其他变量视为常数, 通过多次迭代得到最优解[19]。所以, 由式(17)可以得到以下几个子问题:\mathop {\min }\limits_{s \in {\mathbb{C}^{{N_\theta }}}} \frac{\xi }{2}\left\| {{\boldsymbol{Gs}} - {\boldsymbol{x}} - {\boldsymbol{\lambda}} } \right\|_2^2, (18) \mathop {\min }\limits_{ {x_0} \in {\mathbb{C}^M}} {\iota _{E(\sigma ,{\boldsymbol{y}})}}({{\boldsymbol{x}}_0}) + \frac{\xi }{2}\left\| {{{\boldsymbol{x}}_0} - ({\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}} - {{\boldsymbol{\lambda}} _0})} \right\|_2^2, (19) \mathop {\min }\limits_{ {{\boldsymbol{x}}_1} \in {\mathbb{C}^{^{{N_\theta }}}}} {\left\| {{{\boldsymbol{x}}_1}} \right\|_1} + \frac{\xi }{{2{\alpha _1}}}\left\| {{{\boldsymbol{x}}_1} - ({\boldsymbol{s}} - {{\boldsymbol{\lambda}} _1})} \right\|_2^2, (20) \mathop {\min }\limits_{ {{\boldsymbol{x}}_2} \in {\mathbb{C}^{^{{N_\theta }}}}} {\rm{TV}}({{\boldsymbol{x}}_2}) + \frac{\xi }{{2{\alpha _2}}}\left\| {{{\boldsymbol{x}}_2} - ({\boldsymbol{s}} - {{\boldsymbol{\lambda}} _2})} \right\|_2^2, (21) 式中,
{\boldsymbol{\lambda}} = {[{\boldsymbol{\lambda}} _0^{\rm{H}},{\boldsymbol{\lambda}} _1^{\rm{H}},{\boldsymbol{\lambda}} _2^{\rm{H}}]^{\rm{H}}} 。现在将式(18)—式(21)命名为子问题①—④。问题①中目标函数仅含有一个二次项, 其最优解可以直接由最小二乘解给出:
{\boldsymbol{s}} = {({{\boldsymbol{G}}^{\rm{H}}}{\boldsymbol{G}})^{ - 1}}{{\boldsymbol{G}}^{\rm{H}}}({\boldsymbol{x}} + {\boldsymbol{\lambda}} ). (22) 问题②实际上是在以
{\boldsymbol{y}} 为球心,\sigma 为半径的超球面内部寻找一个{{\boldsymbol{x}}_0} , 使得{{\boldsymbol{x}}_0} 与{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}} - {{\boldsymbol{\lambda}} _0} 之间的距离最小。若{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}} - {{\boldsymbol{\lambda}} _0} 位于超球面内部, 则{{\boldsymbol{x}}_0} 在恰好取到{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}} - {{\boldsymbol{\lambda}} _0} 的时候两者之间距离最小; 若{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}} - {{\boldsymbol{\lambda}} _0} 在超球面外部, 则{{\boldsymbol{x}}_0} 取到{\boldsymbol{y}} 与{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}} - {{\boldsymbol{\lambda}} _0} 之间连线与超球面的交点上的时候, 距离最小, 即问题②的解为{{\boldsymbol{x}}_0} = \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{y}} + \sigma \dfrac{{{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} )s - {{\boldsymbol{\lambda}} _0} - {\boldsymbol{y}}}}{{{{\left\| {{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} )s - {{\boldsymbol{\lambda}} _0} -{\boldsymbol{ y}}} \right\|}_2}}},{\text{ }}{{\left\| {{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}} - {{\boldsymbol{\lambda}} _0} - {\boldsymbol{y}}} \right\|}_2} > \sigma ,} \\ {{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}} - {{\boldsymbol{\lambda}} _0}{\text{, }}\qquad \qquad\, \quad {{\left\| {{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){\boldsymbol{s}} - {{\boldsymbol{\lambda}} _0} - y} \right\|}_2} \leqslant \sigma .} \end{array}} \right. (23) 问题③可以通过软阈值收缩算子[20]进行求解, 其解为
{{\boldsymbol{x}}_1} = {\rm{sof}}{{\rm{t}}_{\tfrac{{{\alpha _1}}}{\xi }}}(\left| {{\boldsymbol{s}} - {{\boldsymbol{\lambda}} _1}} \right|) = {\left(\left| {{\boldsymbol{s}} - {{\boldsymbol{\lambda}} _1}} \right| - \frac{{{\alpha _1}}}{\xi }\right)_ + }{{\rm{sgn}}} ({\boldsymbol{s}} - {{\boldsymbol{\lambda}} _1}), (24) 式中,
{( \cdot )_ + } = \max ( \cdot {\text{ }},0) ,{{\rm{sgn}}} 为符号函数。值得注意的是, 当{\boldsymbol{ s}} - {{\boldsymbol{\lambda}} _1} 为复数的时候, 需要将符号函数替换为\exp ({\rm j}\angle ({\boldsymbol{s}} - {{\boldsymbol{\lambda}} _1})) [14] 。对于问题④的求解, Chambolle提出了一种迭代求解算法, 其具体求解算法可参考文献[21], 这里将问题④的结果记作如下形式:
{{\boldsymbol{x}}_2} = {{\rm{C}}_{\tfrac{{{\alpha _2}}}{\xi }}}(\left| {{\boldsymbol{s}} - {{\boldsymbol{\lambda}} _2}} \right|) = {\rm{C}}{{\rm{P}}_{\tfrac{{{\alpha _2}}}{\xi }}}(\left| {{\boldsymbol{s}} - {{\boldsymbol{\lambda}} _2}} \right|){{\rm{sgn}}} ({\boldsymbol{s}} - {{\boldsymbol{\lambda}} _2}). (25) 与问题③一样, 当
{\boldsymbol{s}} - {{\boldsymbol{\lambda}} _2} 为复数的时候, 需要将符号函数替换为\exp ({\rm j}\angle ({\boldsymbol{s}} - {{\boldsymbol{\lambda}} _2})) 。综上, 得到了式(12)优化问题的迭代求解算法, 如下所示。
约束分裂增广拉格朗日收缩算法(CSALSA) 输入: {\boldsymbol{y}}, \quad \xi > 0, \quad {\boldsymbol{x}}^{(0)}= \mathbf{0}, \quad \lambda^{(0)}=\mathbf{0},\quad \alpha_1 > 0, \quad \alpha_2 > 0, \quad \alpha_1+\alpha_2=1 {\rm{for}}\; k = 0:K - 1 {{\boldsymbol{s}}^{(k + 1)}} = {({{\boldsymbol{G}}^{\rm{H}}}{\boldsymbol{G}})^{ - 1}}{{\boldsymbol{G}}^{\rm{H}}}({{\boldsymbol{x}}^{(k)}} + {{\boldsymbol{\lambda}} ^{(k)}}), {\boldsymbol{x}}_0^{(k + 1)} = \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{y}} + \sigma \dfrac{{{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){{\boldsymbol{s}}^{(k + 1)}} -{\boldsymbol{ \lambda}} _0^{(k)} - {\boldsymbol{y}}}}{{{{\left\| {{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _0^{(k)} - y} \right\|}_2}}}{\text{, }}\quad\quad{{\left\| {{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _0^{(k)} - {\boldsymbol{y}}} \right\|}_2} > \sigma, } \\ {{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _0^{(k)}{\text{, }}\quad\quad\quad\qquad\qquad{{\left\| {{\boldsymbol{A}}(\overline \theta ){{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _0^{(k)} - y} \right\|}_2} \leqslant \sigma, } \end{array}} \right. {\boldsymbol{x}}_1^{(k + 1)} = {\rm{sof}}{{\rm{t}}_{\tfrac{{{\alpha _1}}}{\xi }}}\left(\left| {{{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _1^{(k)}} \right|\right), {\boldsymbol{x}}_2^{(k + 1)} = {{\rm{C}}_{\frac{{{\alpha _2}}}{\xi }}}\left(\left| {{{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _2^{(k)}} \right|\right), {{\boldsymbol{\lambda}} ^{(k + 1)}} = {{\boldsymbol{\lambda}} ^{(k)}} + {{\boldsymbol{x}}^{(k + 1)}} - {\boldsymbol{G}}{{\boldsymbol{s}}^{(k + 1)}} {\rm{end}} 输出: {{\boldsymbol{s}}^{(K)}} 2.3 宽带处理方法
上述算法是在窄带情况下进行推导, 然而在实际探测当中, 为了同时获得时间向的高分辨能力, 往往需要使用宽带信号, 所以需要进一步将上述算法推广到宽带情况下。对于宽带信号而言, 无法直接写为式(7)形式的模型并通过稀疏优化算法进行求解。通过将阵列接收信号变换至频域, 可以写出在频点
{f_{{n'}}} 处的频域单快拍模型如下:\mathcal{Y}({f_{{n'}}}) = {\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ,{f_{{n'}}})\mathcal{S}({f_{{n'}}}) + \mathcal{{{N}}}({f_{{n'}}}). (26) 根据式(26), 可以在每个频点上通过上述算法得到该频点下的方位估计结果, 最终得到方位频率强度图。虽然理论上可以通过对每个方向上的频域估计信号进行傅里叶逆变换得到方位时间强度图, 但是稀疏优化类算法估计结果较为依赖参数选取, 不合适的参数会导致功率估计误差, 而这一误差在经傅里叶逆变换后导致最终得到的时间方位强度图中目标出现模糊, 效果不佳。而对信号进行时域分段处理的方式, 虽然可以得到时间方位强度图, 但是分段长度
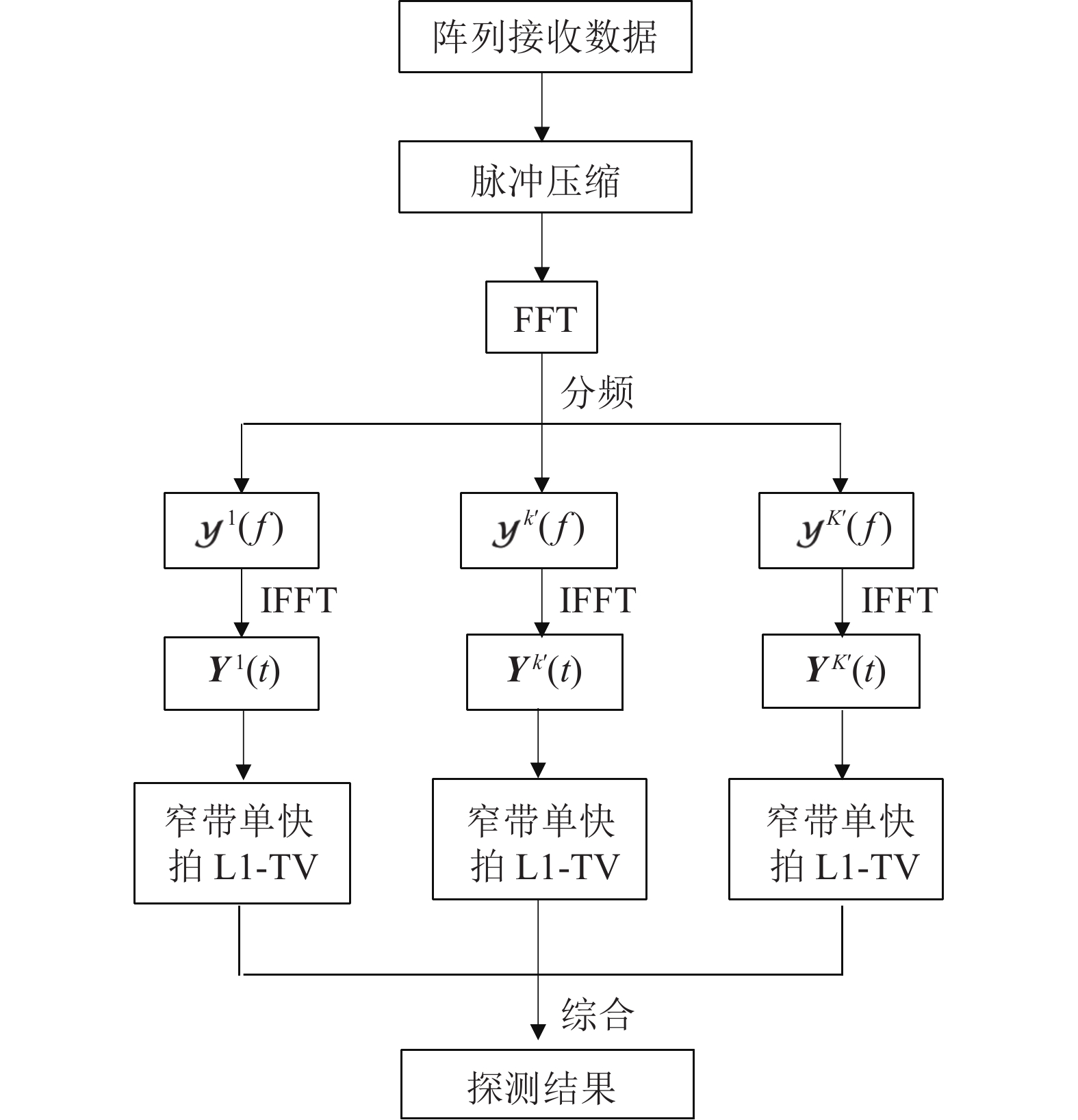
\Delta t 往往要大于宽带信号的时间分辨能力1/B , 从而造成时间向分辨能力的损失。为使所提算法应用于方位向上的处理时不损失宽带信号带来的高时间分辨能力, 本文提出使用如下方式对宽带信号进行处理。首先, 对阵列接收信号
{\boldsymbol Y}(t) 进行傅里叶变换得到频域接收信号\mathcal{Y}(f) 。假设其有效带宽范围从{f_L} 到{f_H} , 带宽为B , 通过\mathcal{Y}(f) 与长度为\Delta f 的矩形窗函数相乘, 将\mathcal{Y}(f) 在其有效带宽内分为{K'}{\text{ }}({K'} = B/\Delta f) 个不重叠的子带频域信号, 为了保证每个子带能够近似为窄带信号,\Delta f 的长度需要满足窄带条件, 即\Delta f/f \ll 1 。其中一个窄带信号的表达式如下:{\mathcal{Y}}^{k'}(f)=\left\{\begin{array}{l}{\mathcal{Y}}(f),\qquad\;\;\;{f}_{L}\leqslant f\leqslant {f}_{L} + {k}{{'}}\Delta f,\\ 0,\qquad\qquad 其他.\end{array}\right. (27) 对
\mathcal{Y}^{k'}(f) 行逆变换得到{{\boldsymbol{Y}}^{{k'}}}(t) , 而{{\boldsymbol{Y}}^{{k'}}}(t) 可以视作频率为{f_L} + {k'}\Delta f/2 的时域窄带信号, 尽管这里用每个子带的中心频率来代替整个子带会引入少量的误差, 但是只要子带的划分宽度\Delta f 满足窄带条件\Delta f/f \ll 1 , 这个误差实际上是相当小的, 几乎不会对最后结果产生影响。这样,{{\boldsymbol{Y}}^{{k'}}}(t) 可以写为式(28)的形式, 即在{t_i} 时刻的时域模型如下:{{\boldsymbol{Y}}^{{k'}}}({t_i}) = {\boldsymbol{A}}\left(\overline {\boldsymbol{\theta}} ,{f_L} + \frac{{{k'}\Delta f}}{2}\right){{\boldsymbol{S}}^{{k'}}}({t_i}) + {{\boldsymbol{N}}^{{k'}}}({t_i}). (28) 通过以上所述处理方式, 将宽带接收时域信号分成了
{K'} 个窄带接收时域信号, 对于每个{{\boldsymbol{Y}}^{{k'}}}(t) 就能够使用所提出的算法对其进行逐快拍处理(为了加快计算, 可以将一个时间分辨单元内的快拍平均后进行处理[22]), 这样每个窄带时域信号{{\boldsymbol{Y}}^{{k'}}}(t) 均可以得到一个方位时间强度探测结果, 将不同{{\boldsymbol{Y}}^{{k'}}}(t) 得到的探测结果进行平均即可得到最终的探测结果。宽带信号的处理流程如图2所示。3. 仿真实验
3.1 一维窄带方位估计仿真分析
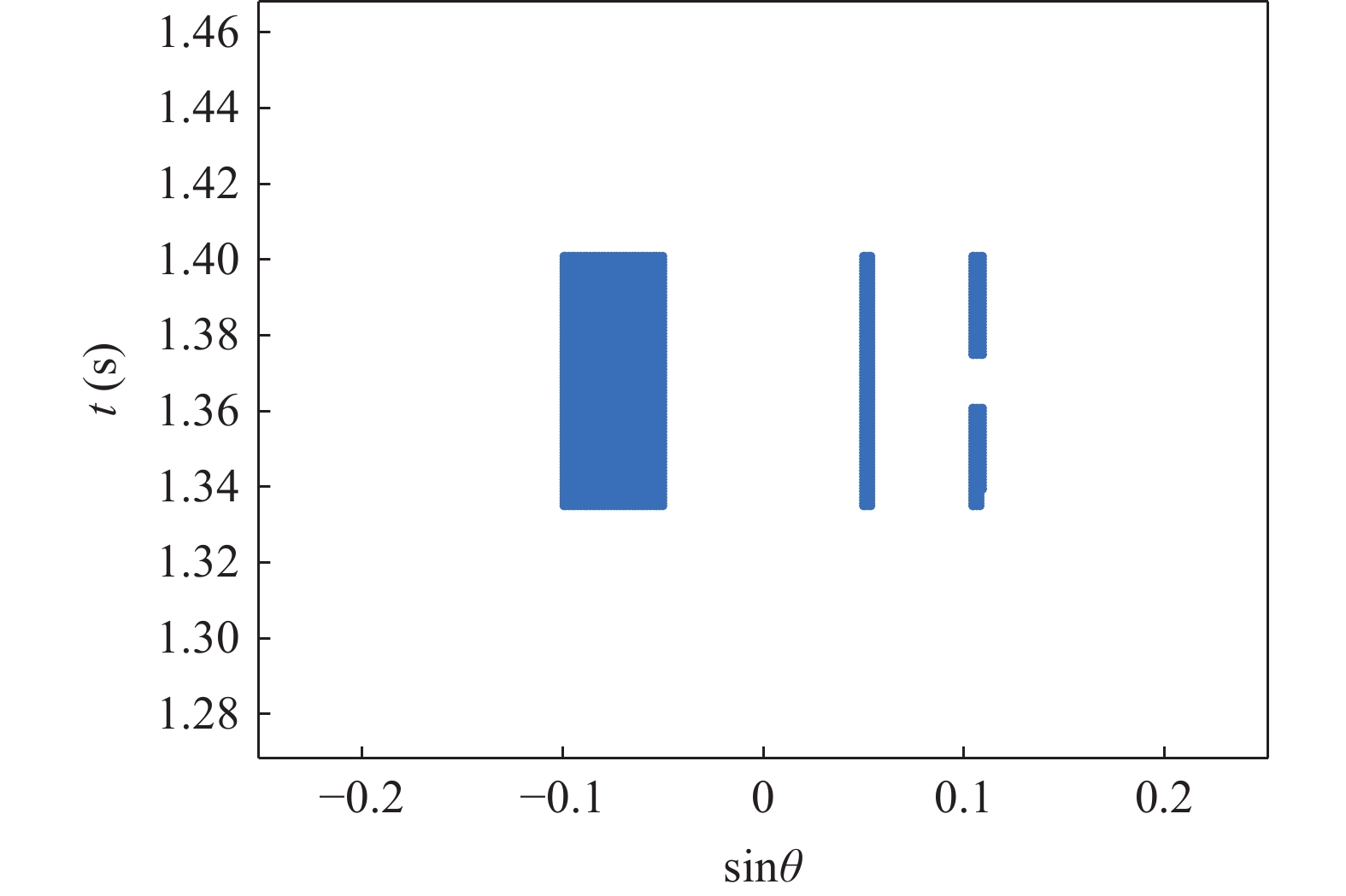
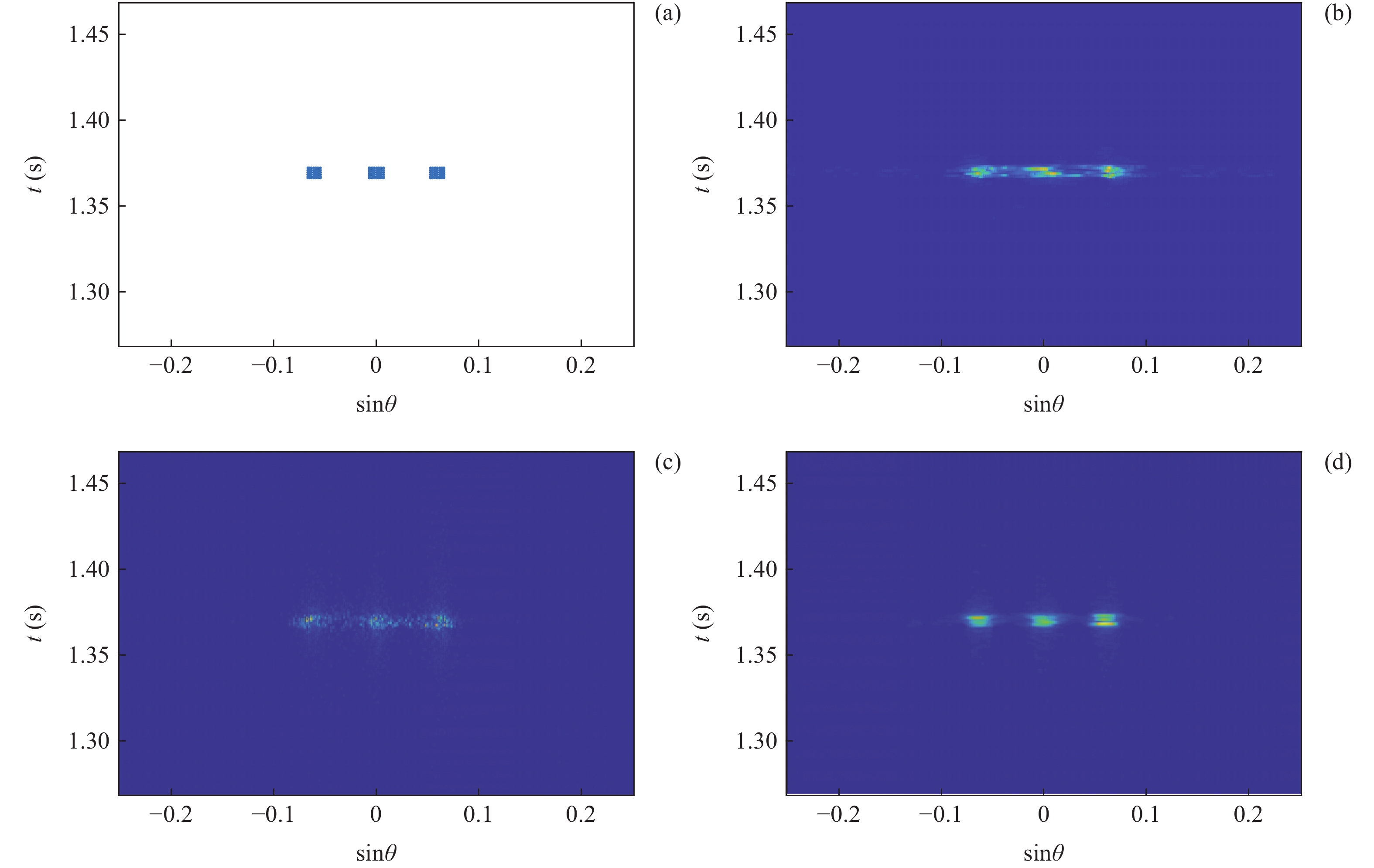
在一维窄带单快拍情况下, 对所提算法的方位估计性能及性能进行仿真验证, 并将结果与常规波束形成算法、解卷积后处理算法及基于1范数正则化算法(cvx软件包求解)进行对比。本次仿真中, 来波并不来自某几个单一方位, 而是在一定方位范围内连续存在, 图3(a)给出了本次仿真中来波方位分布情况。使用的仿真参数如下: 阵列采用半波长布阵的均匀直线阵, 阵元数为41, 接收信噪比为15 dB, 划分网格数为512, 算法参数
\xi = 10 ,{\alpha _1} = 0.85 ,{\alpha _2} = 0.15 。得到的仿真结果如图3(b)— 图3(e)所示。从上面的仿真结果可以看出, 常规波束形成算法的分辨率较低, 无法分辨右侧两个方位上间隔较小的目标, 且对左侧目标的估计结果在方位上存在较大的扩展。解卷积后处理方法与1范数正则化方法的方位分辨能力明显提升, 但是在连续存在来波的角度区域估计结果极度不平滑, 出现了多个孤立峰, 失真较为严重, 并且解卷积算法还出现了较为明显的伪峰。而所提出的混合1范数与全变分正则化方法, 通过CSALSA进行求解后, 不仅在分辨率上有所提高, 并且在连续存在来波的角度区域估计结果较为平滑, 边缘陡峭, 整体结果与真实情况更加接近, 失真较小。
3.2 二维宽带探测场景下仿真分析
在二维宽带探测场景下对所提算法进行验证之前, 需要对各阵元接收数据进行仿真。对于第1节中的探测场景, 阵元接收信号主要由两部分组成, 目标回波与海底混响信号, 本文对两者分别进行仿真, 然后根据式(5)计算的信混比将两者在相应的时刻叠加得到仿真数据, 下面对信号生成模型进行具体介绍。
信号生成采用点散射法, 其主要思想是将目标离散成为大量的随机散射点, 通过计算各个散射点的回波并叠加, 从而得到回波信号[23]。该方法有较为明确的物理意义, 也是一种常用的验证成像算法性能的信号生成方法。将设置目标离散成大量随机散射点, 为了能够对连续目标进行模拟, 这些散射点在方位向上的平均间隔要小于成像探测所使用的网格间隔, 而在时间向上的平均间隔要小于所使用的宽带信号的时间分辨单元。设生成的散射点总数为
I , 第i 个散射点的坐标为{{\boldsymbol{p}}_i} , 发射信号频域记作\mathcal{X}(f) ,m 号阵元的坐标为{{\boldsymbol{p}}_m} , 则m 号阵元接收到的目标回波信号在频域可以表示为\sum\limits_i^I {\frac{{{\rho _i}}}{{\left| {{{\boldsymbol{p}}_i}} \right|\left| {{{\boldsymbol{p}}_i} - {{\boldsymbol{p}}_m}} \right|}}} \mathcal{X}(f)\exp \left( { - {\rm{j}}2\pi f\frac{{\left| {{{\boldsymbol{p}}_i}} \right| + \left| {{{\boldsymbol{p}}_i} - {{\boldsymbol{p}}_m}} \right|}}{c}} \right), 其中,
{\;\rho _i} 为第i 个散射点的散射系数, 该值与目标的材质有关, 对于同类目标{\;\rho _i} 都相同; 而指数项则是代表信号经发射传播至第i 个散射点再散射回m 号阵元过程中产生的时延而造成的相移, 对于不同频率产生的相移并不相同。海底混响为本文探测场景中主要的背景干扰, 其来自于发射激励扇面内的各个方向, 具有方向性, 而这一特性可能会影响稀疏先验条件。为了验证本文所提算法在海底混响条件下的有效性, 对海底混响信号的仿真同样采取点散射法, 该方法能够保证生成混响信号的方向特性与各个阵元之间混响信号的空间相关性。将目标所在区域附近的一片海底离散为
L 个散射点, 同理可以得到m 号阵元接收到的海底混响频域表达式为\sum\limits_l^L {\frac{{{\rho _l}}}{{\left| {{{\boldsymbol{p}}_l}} \right|\left| {{{\boldsymbol{p}}_l} - {{\boldsymbol{p}}_m}} \right|}}} {\mathcal{X}_l}(f)\exp \left( { - {\rm{j}}2\pi f\frac{{\left| {{{\boldsymbol{p}}_l}} \right| + \left| {{{\boldsymbol{p}}_l} - {{\boldsymbol{p}}_m}} \right|}}{c}} \right)\exp ( - {\rm{j}}{\phi _{{\text{ }}l}}), 其中,
{\rho _l} 为兰伯特散射系数,{\phi _{{\text{ }}l}} 为[0,2\pi ] 之间的随机相位跳变, 并且考虑到掠射角较低与复杂的海底环境, 海底散射波与发射信号在波形上畸变严重, 所以对于每个散射点, 其回波使用的是与发射信号同脉宽、同带宽的带限噪声。实际上, 影响混响空间特性的主要因素是离散点回波到各个阵元之间的时延差异, 即上面表达式中的指数项。至此, 通过点散射法仿真得到了目标回波信号与海底混响信号。设目标回波的起始时刻为
{t_1} , 结束时刻为{t_2} , 则可以计算出目标的平均功率{P_{{\rm{tar}}}} , 同样地可以计算出混响信号在{t_1} 至{t_2} 时刻之间的平均功率{P_{{\rm{rev}}}} , 通过调整目标回波的整体幅度, 使得其满足下面的信混比定义表达式, 然后与混响信号在相应的时刻进行叠加则可以得到最终的仿真信号:{R_{\rm SR}} = 10\lg \left(\frac{{{P_{{\rm{tar}}}}}}{{{P_{{\rm{rev}}}}}}\right). (29) 设置的海底目标如图4所示, 左侧为一个大型连续目标, 用于验证算法对连续扩展目标的估计能力, 而右侧是多个相隔较近的棒状目标, 用于验证算法的分辨能力。需要说明的是这里设置的目标仅是为了对所提算法性能进行验证, 并没有考虑阴影。
仿真使用的参数如下: 设备距离海底高度为50 m, 发射扇面开角为60°, 发射信号为宽带线性调频波, 中心频率为20 kHz, 带宽为5 kHz, 脉宽为50 ms, 接收阵列为半波长布阵的均匀直线阵, 阵元数为35, 接收信号在带宽内被分为10个不重叠的子带, 每个子带500 Hz。设置的目标如图4所示, 从左往右目标强度依次为20 dB, 17 dB, 15 dB, 15 dB, 海底底质考虑砂砾沉积物, 对应的兰伯特常数
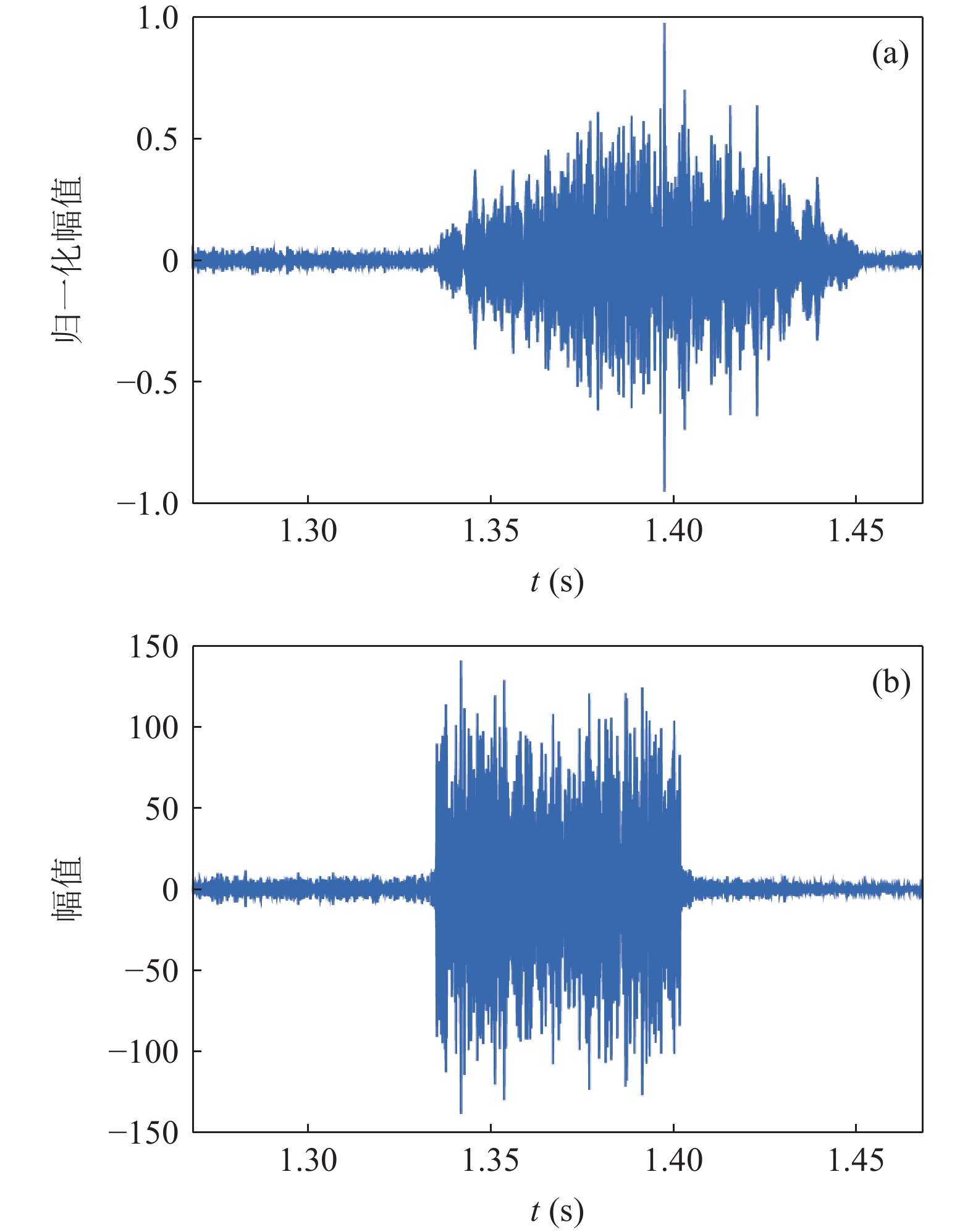
10\lg \mu = - 19 [24]。根据式(5)计算出各个目标的回波信混比为19 dB, 16 dB, 14 dB, 14 dB。图5展示了阵列中心阵元的接收信号的仿真结果以及匹配滤波后的波形。利用本文提出的算法对仿真信号进行处理, 得到的结果如图6所示, 此外还给出了白噪声背景下的处理结果作为对比项, 在下文中, 如无其他特别说明, 海底混响背景指算法仿真的背景干扰为由点散射法生成的海底混响, 而白噪声背景则是指算法仿真的背景干扰仅含有高斯白噪声。
从仿真结果可以看出, 本文算法不仅成功分辨了右侧目标, 而且多个目标边界较为清晰, 与背景的对比度强。此外, 对比图6(a)(b), 可以发现即使在加入海底混响背景后本文算法仍然有效, 只是需要更大的惩罚因子
\xi , 关于这一点将在后文进一步分析。以上只是从主观感受出发进行评价, 还需要从客观上进行评价。图像领域中常使用均方误差(MSE)衡量结果与真实值之间的差距, 但是该指标会过于关注图像在像素级上的差距, 忽略结构上的信息[25]。而本文算法的目的是通过回波信号估计目标在方位时间上的分布, 即更加关注目标的结构信息, 所以在这里引入二值化方法[26], 通过对估计结果进行二值化的处理, 突出结构信息后再与设置目标进行对比求总平方误差(TSE), 将该值作为衡量估计结果好坏的指标。需要说明的是, 二值化后使用TSE而不使用MSE 的原因是本文仿真设置场景中存在大量的背景空白, 求均值后会导致MSE很小, 不够直观。
首先将探测归一化结果
{\boldsymbol{Q}} 进行二值化,{\boldsymbol{Q}} 中大于阈值TH的值被设为1, 而小于阈值TH的值被设为0, 得到{{\boldsymbol{Q}}_{{\rm{bi}}}} ;{{\boldsymbol{Q}}_{{\rm{bi}}}} 能够很好的凸显{\boldsymbol{Q}} 中目标的结构外形特征。然后将{{\boldsymbol{Q}}_{{\rm{bi}}}} 与真实目标{{\boldsymbol{Q}}_{{\rm{re}}}} 逐点计算误差的大小, 得到其总的平方误差:{\rm{TSE }}= \left\| {{{\boldsymbol{Q}}_{{\rm{bi}}}} - {{\boldsymbol{Q}}_{{\rm{re}}}}} \right\|_{\rm{F}}^2. (30) 在评价过程中, 二值化阈值TH采用自适应迭代选定, 将其初值设为0.5, 以其为界限将
{\boldsymbol{Q}} 中的所有值分为两部分, 计算这两部分的平均值{g_1} 与{g_2} , 将({g_1} + {g_2})/2 作为新的阈值, 循环上述步骤多次迭代可以收敛得到最佳二值化阈值。通过以上计算得到的TSE可以在一定程度上反应估计结果的优劣, 该值越低说明估计结果与真实目标更加接近, 性能也越好。下面利用该评价指标, 探究不同的算法参数对所提出算法性能的影响以及各算法性能随信混比的变化。
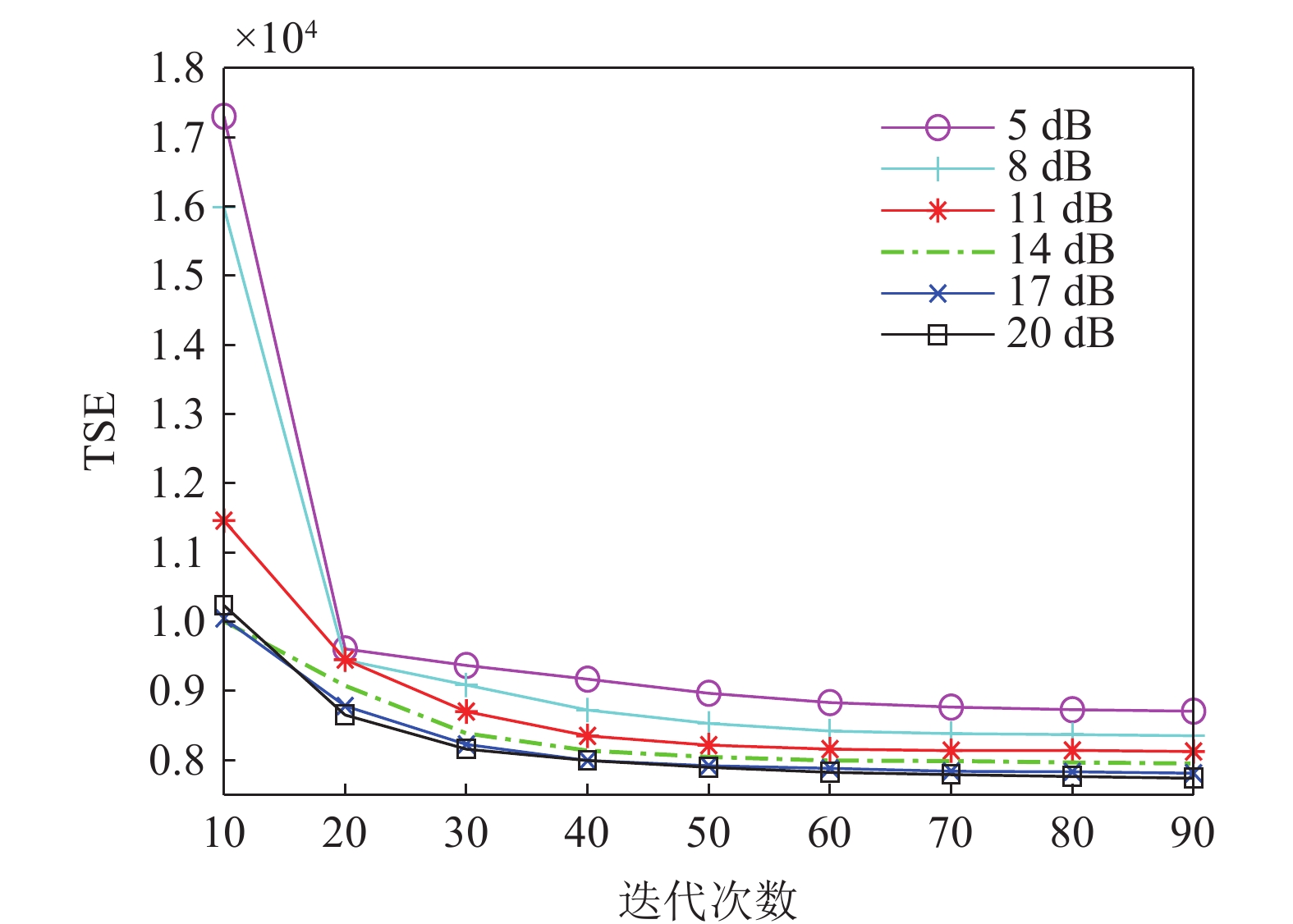
(1) 算法迭代次数的影响
算法的迭代次数会对最后的估计结果产生影响, 当迭代次数较小时, 算法没有收敛完全, 而当迭代次数过大时, 则会加大计算上的压力。为了确定合适的算法迭代次数, 保持上述仿真条件不变, 在图7给出算法的TSE随着迭代次数变化的曲线。随着算法的迭代次数的增加, TSE逐渐下降, 并且下降速率逐渐放缓, 当迭代次数达到60, 随着迭代次数增多, TSE变化不明显, 说明此时算法已经基本收敛。出于算法性能与计算量的考虑, 算法的迭代次数需要大于60。
(2) 算法参数的影响
本文所提的混合1范数与全变分正则化稀疏重构算法的输入参数, 包括1范数约束项的系数
{\alpha _1} 、全变分的约束项系数{\alpha _2} 以及惩罚因子\xi , 均会对算法最终的成像探测性能造成影响, 下面将对各个参数的具体影响进行讨论, 并针对文章中的仿真场景选取相对合适的参数值。首先对优化模型中
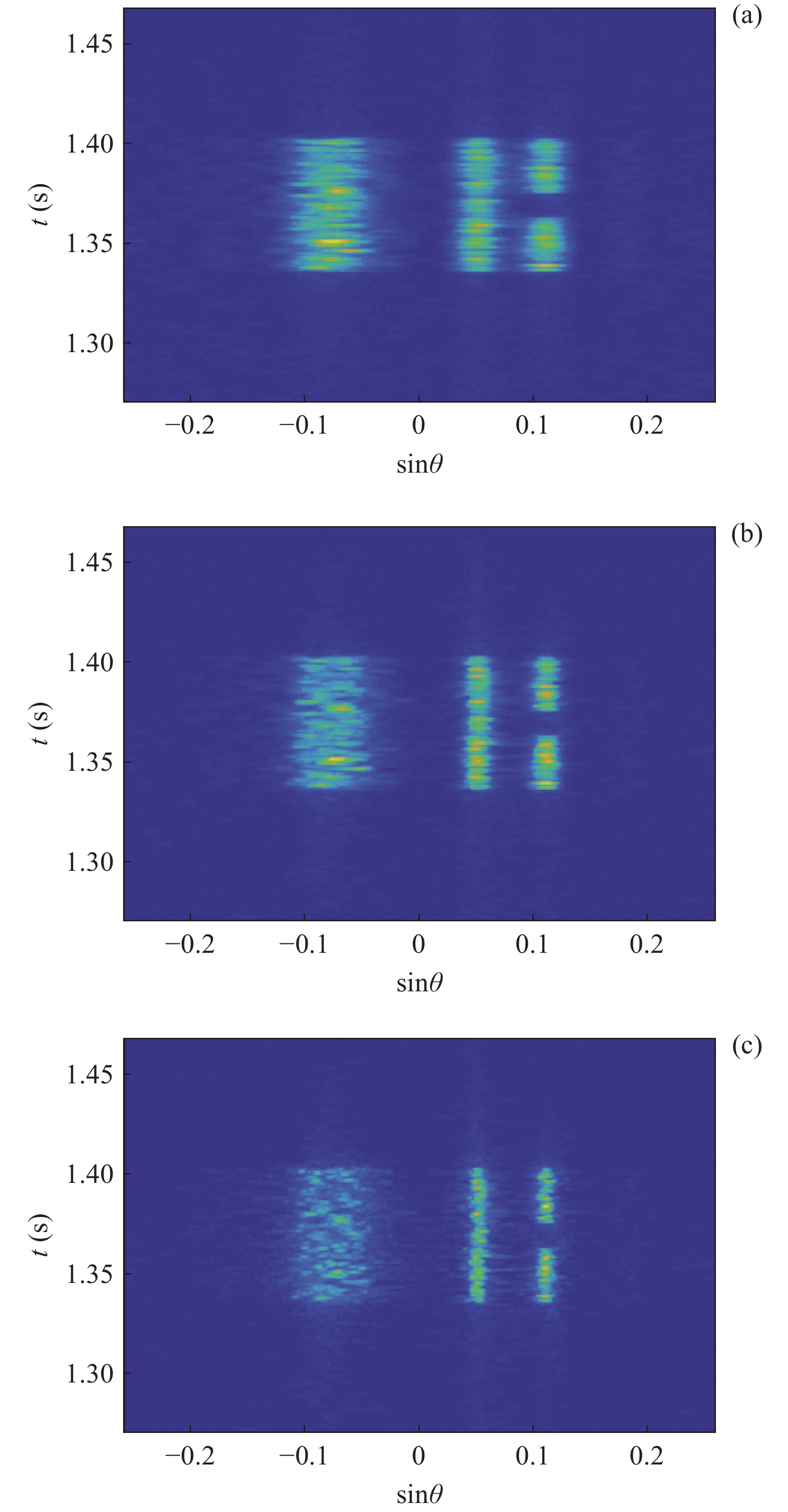
{\alpha _1} 与{\alpha _2} 两个参数对成像结果的影响进行讨论。保持上述仿真参数不变化, 仅改变{\alpha _1} 与{\alpha _2} 的大小, 图8给出了不同加权参数下的估计结果对比。可以看出当{\alpha _1} 较小的时候, 估计结果在方位向的分辨率较低, 目标扩展更宽; 随着{\alpha _1} 增大, 估计结果的分辨率出现了明显的提升; 继续提升{\alpha _1} 到0.99, 此时分辨率的提升较小, 但是由于此时{\alpha _2} 较小, 导致左侧的方位扩展目标内部平滑性下降, 出现了明暗相间的纹路, 且与背景之间对比度下降。图9给出了蒙特卡洛平均后, 估计结果TSE随模型加权参数
{\alpha _1} 的变化曲线。可以看出随着{\alpha _1} 的增大, 估计结果的TSE逐渐降低, 当{\alpha _1} 在0.9附近时TSE达到最低, 之后继续增大{\alpha _1} , TSE并没有继续降低, 反而有一定程度的升高, 这也与图8基本一致。出现这种现象主要因为{\alpha _1} 与{\alpha _2} 在本算法中控制着1范数约束与全变分约束的比例, 而1范数约束主要影响算法的分辨率, 全变分约束影响结果的分段平滑特性。当{\alpha _1} 较小的时候, 1范数约束所占比例较小, 算法的分辨能力较低, 因此估计结果与设置目标相差较大, TSE较高; 而{\alpha _1} 增高后, 算法分辨能力增高, 估计结果与设置目标更接近, TSE迅速下降; 然而当{\alpha _1} 增高到某个界限后, 继续增高对分辨率的提升较小, 反而由于{\alpha _2} 的降低, 全变分约束所占比例减小, 目标内部的平滑性下降, 导致TSE增高, 这一点对于左侧方位扩展目标更加显著。图9的曲线仅针对本文的仿真场景, 对于不同的场景,{\alpha _1} 与{\alpha _2} 的最佳取值可能发生改变, 可以预见, 当目标方位扩展更大时,{\alpha _1} 取值应该更小, 反之当目标更加接近点目标时{\alpha _1} 取值应该更大。实际中需要结合应用场景以及关注点进一步调优, 以获得更好的结果。惩罚因子
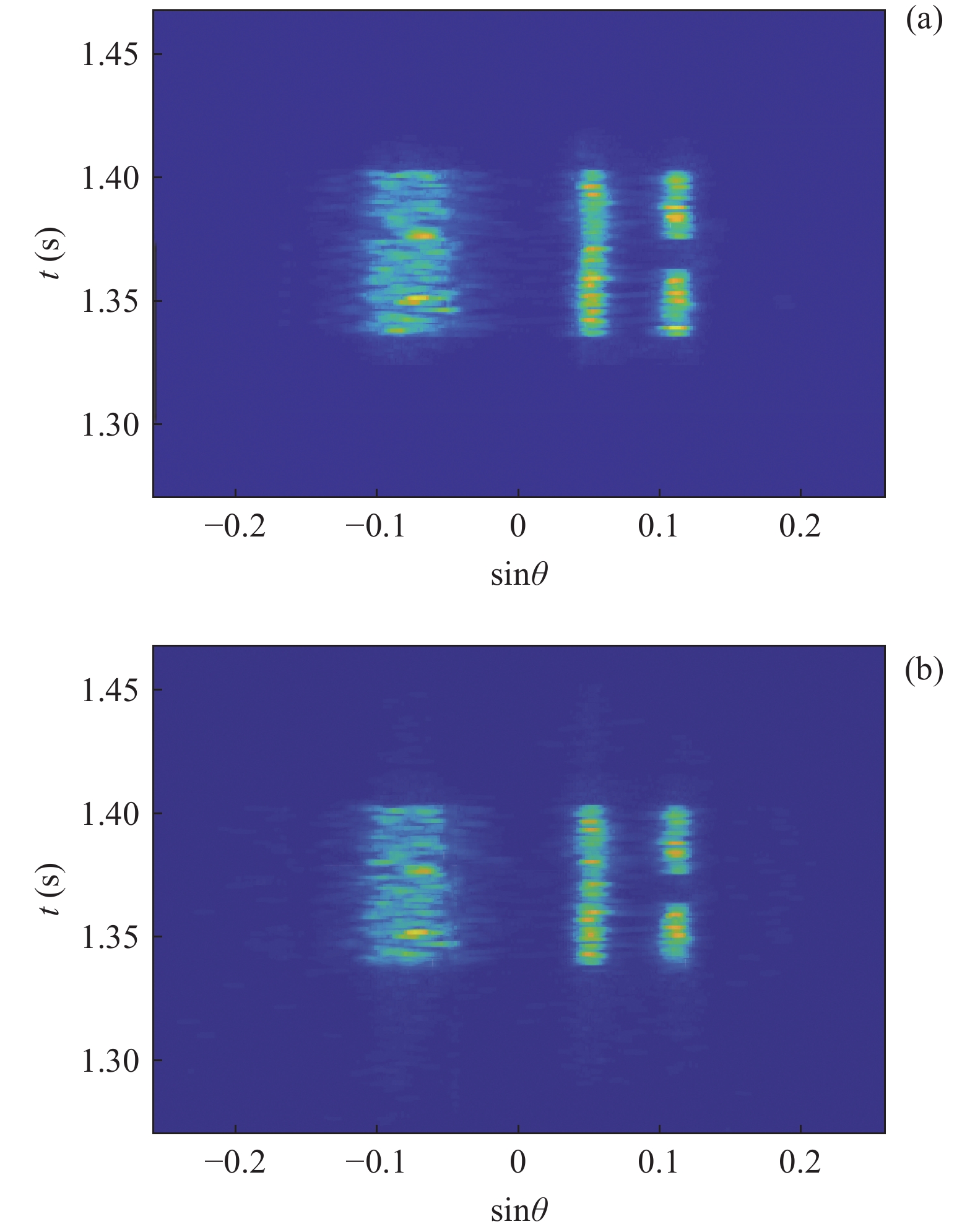
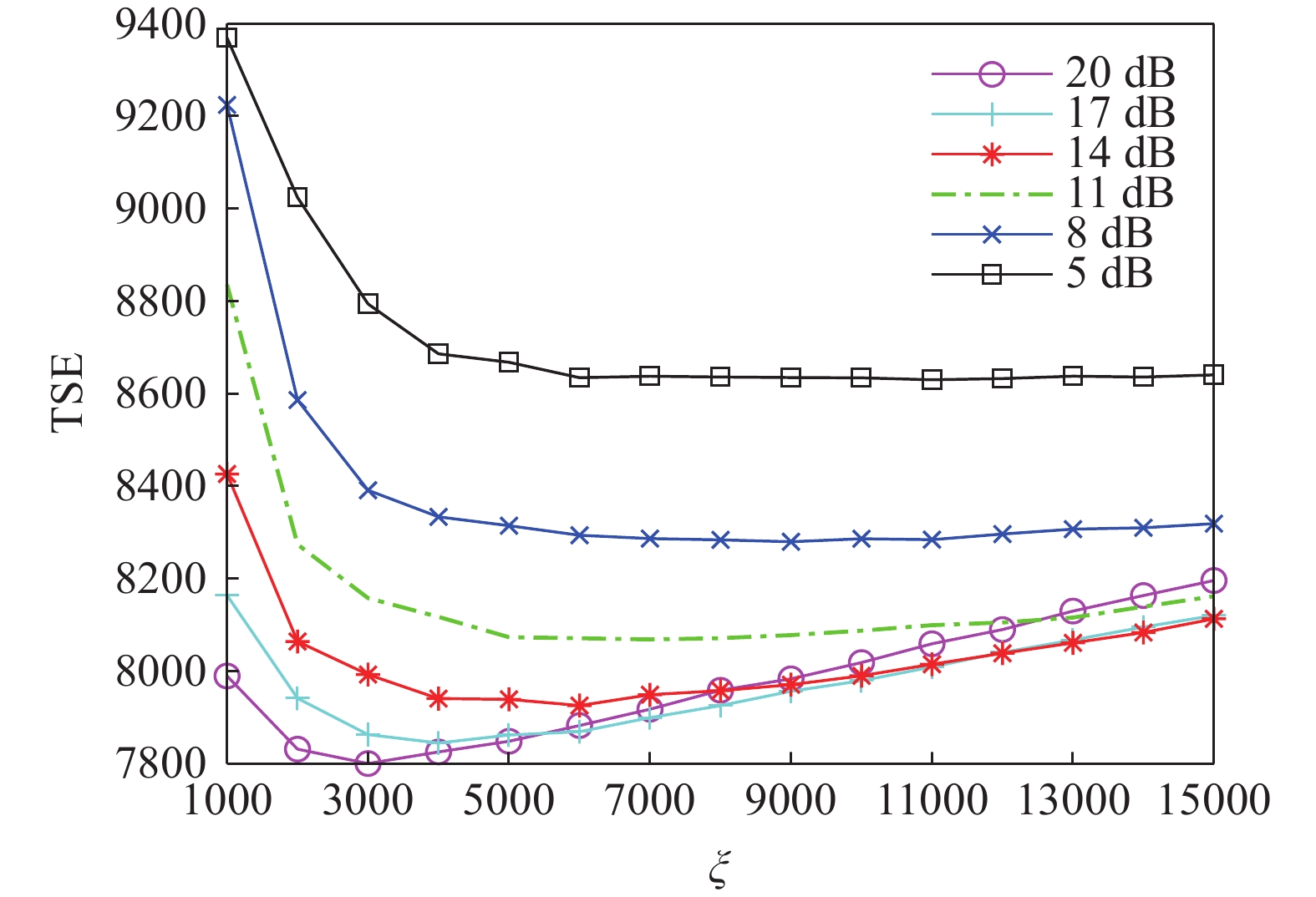
\xi 同样会对算法结果产生影响, 由图6的仿真可知, 本文算法虽然在海底混响背景下仍然有效, 但是相比白噪声背景下需要更大的惩罚因子\xi 。为了探究该参数的具体影响, 在海底混响的背景下, 改变信混比大小, 并对每个信混比计算了不同惩罚因子\xi 下的TSE, 最终结果如图10所示。从仿真结果可以看出, 随着惩罚因子
\xi 的增大, 估计结果的TSE呈现先下降再上升的过程, 即对于每个信混比, 均存在一个最佳的惩罚因子\xi ; 此外, 在低信混比下, 最佳惩罚因子\xi 会更大。这里对上述现象的产生原因及\xi 的具体影响进行分析。在式(16)中,{\boldsymbol{s}} 为最终需要求解的变量,{\boldsymbol{x}} 为引入的中间变量, 而实际上是将保真约束、1范数约束以及全变分约束施加在{\boldsymbol{x}} 上, 然后通过{\boldsymbol{Gs}} - {\boldsymbol{x}} = {\boldsymbol{0}} 这一等式约束去影响最终求解变量s 。在式(17)中,{\boldsymbol{Gs}} - {\boldsymbol{x}} 被作为惩罚项加入了增广拉格朗日函数,\xi 为惩罚因子, 增大\xi 会使{\boldsymbol{Gs}} - {\boldsymbol{x}} = {\boldsymbol{0}} 这一约束更加严格, 从而导致施加在{\boldsymbol{x}} 上的约束对{\boldsymbol{s}} 的影响会更强。进一步求解式(17) , 可以发现施加保真约束的中间变量{{\boldsymbol{x}}_0} 的迭代式(23)中, 其实并不含\xi , 而施加1范数约束与全变分约束的中间变量{{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2} 的迭代式(24)和式(25)中才含有\xi , 所以增大\xi 的最终效果相当于通过{\boldsymbol{Gs}} - {\boldsymbol{x}} = 0 整体上加强了对s 的1范数约束与全变分约束。在混响背景下, 海底混响的存在会一定程度上影响稀疏先验条件, 因此需要比白噪声环境下更大的\xi (本文场景中相差4个数量级)来加强先验约束, 迫使最终解向符合先验约束的方向接近。这也较好地解释了为什么同样在混响背景下, 信混比越低所需要的\xi 值越大, 因为低信混比下混响较强, 对稀疏先验的影响也就越大, 需要更大的惩罚因子\xi 来加强约束。(3) 各算法性能随信混比的变化
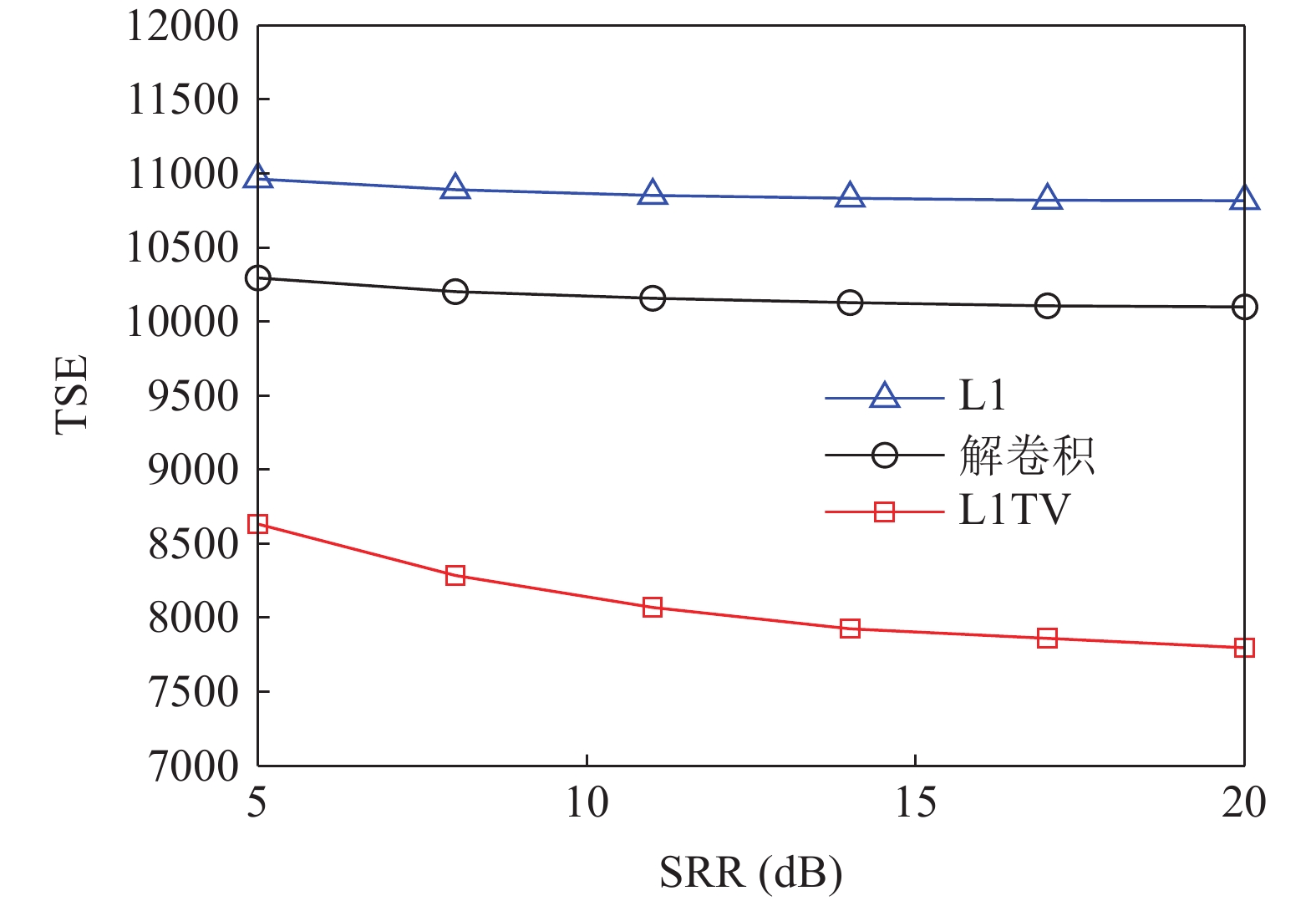
与上文中一维情况下的仿真类似, 这里同样选取常规波束形成算法、解卷积后处理算法与基于1范数正则化算法(cvx软件包求解)作为本文提出算法对比项。保持图6的仿真条件不变, 改变信混比为20 dB, 如无其他说明, 这里与下文的信混比指的是左侧目标的信混比, 右侧几个目标在此基础上分别下降3 dB, 5 dB, 5 dB。各算法的估计结果如图11所示。
将估计结果与设置目标对比可以看出, 常规波束形成的方位分辨能力较差, 对右侧间隔较小的目标无法分辨, 并且由于旁瓣泄露在无目标的区域也出现了亮斑; 解卷积后处理算法虽然方位分辨能力有所提高, 但是对右侧目标的分辨较为模糊, 目标边界也不够清晰; 基于1范数正则化的稀疏恢复算法基于点目标假设, 导致其探测结果中连续的扩展目标被离散为一系列孤立亮点, 呈现点云形式; 而本文所提出的算法不仅在方位分辨能力上有了较好的提升, 并且目标亮度均匀, 边界清晰度也有了较好的提升, 总体上要优于对比算法。同时计算得到各个算法估计结果的TSE如表1所示。
表 1 图11中各算法估计结果TSECBF 解卷积 1范数正则化 L1TV TSE 21648 10115 10863 7781 改变信混比, 通过多次计算平均得到图12中各算法TSE随信混比变化的曲线, 算法参数按照图9和图10中的讨论结果进行选取。图13给出了本文所提算法在不同信混比下的估计结果, 以便直观地观察算法性能随信混比的变化。
由图12可以看出, 本文算法的TSE在整体上均优于另外两种算法。随着信混比的增加, 解卷积算法与1范数正则化算法的TSE下降不明显, 这是因为解卷积算法是以常规波束形成结果为基础进行后处理, 而常规波束形成算法稳健性较高, 其性能在图12中的信混比范围内变化不明显; 1范数正则化算法估计结果呈现孤立点云的形式, 即使随着信混比变化点云的范围发生改变, 但这种改变反映到TSE上实际上并不明显。相比而言, 虽然本文所提出的混合L1TV稀疏重构算法的TSE随着信混比的下降出现了明显的升高, 但其性能仍然优于其他两种算法。另外, 对于算法本身而言, 由图13可以看出, 低信混比下本文算法的估计结果出现了下降, 表现为背景出现噪点, 目标边界更加模糊, 所以为了保证本算法能够取得足够好的成像结果, 建议回波信混比大于10 dB。
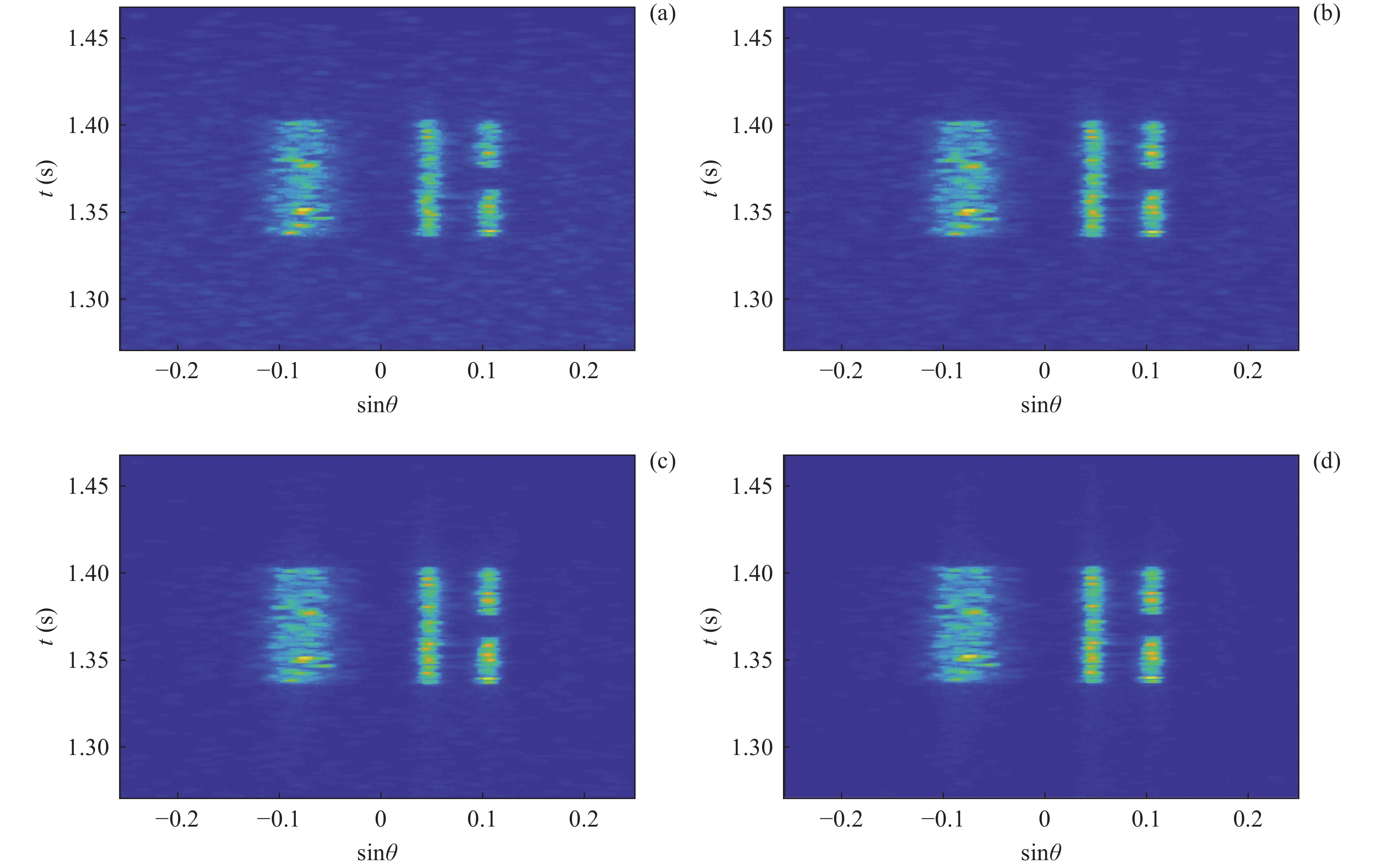
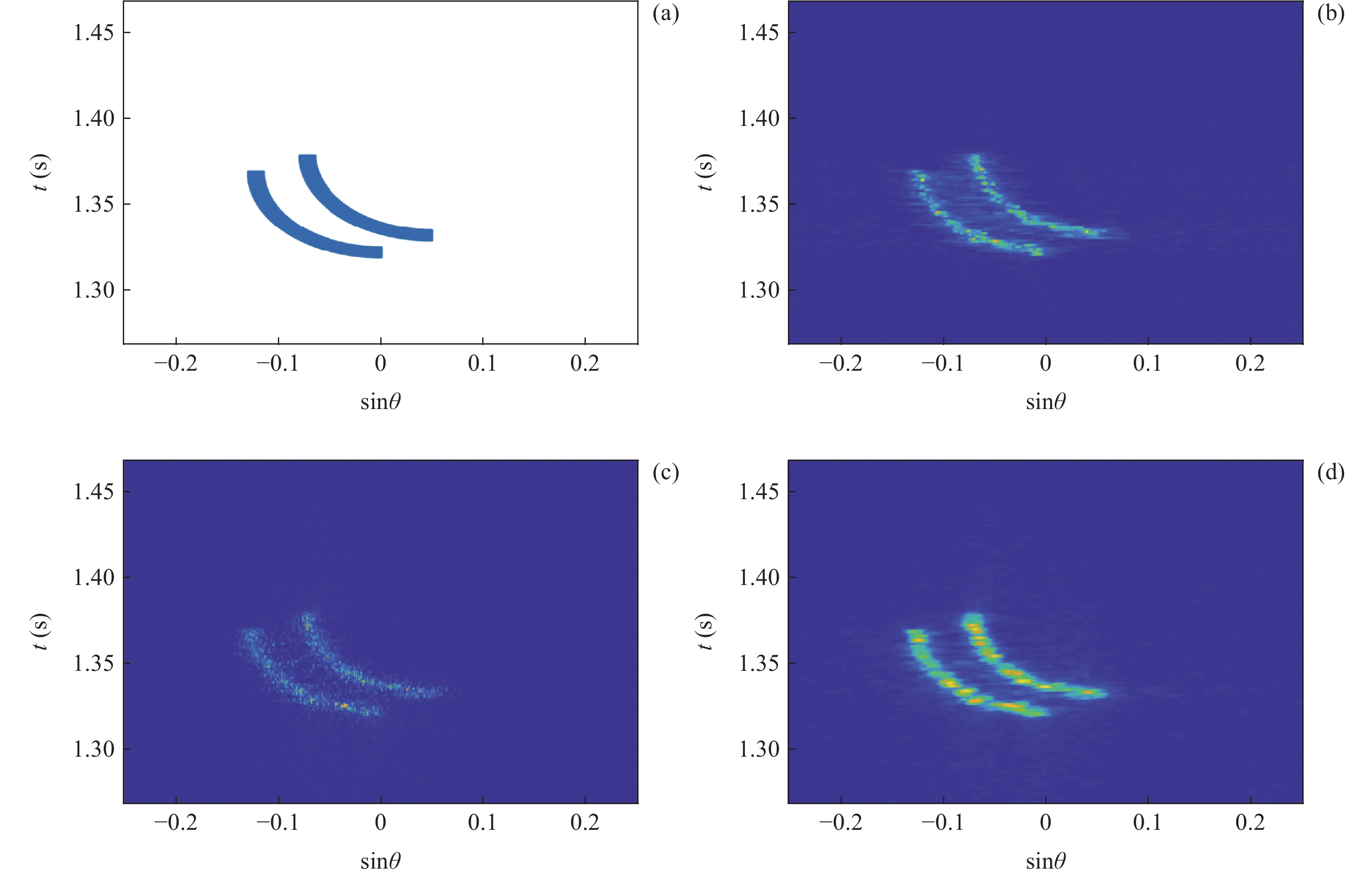
此外, 为了证明本文算法的有效性与优越性, 还针对弯曲目标与小目标进行了仿真, 并将仿真结果与其他算法的估计结果进行了对比。仿真结果如图14与图15所示, 表2与表3中给出了各个算法下的TSE数值。对于不同形状类型的目标, 本文算法均取得了更佳的估计结果, 从而证明了本算法具有一定的普适性。
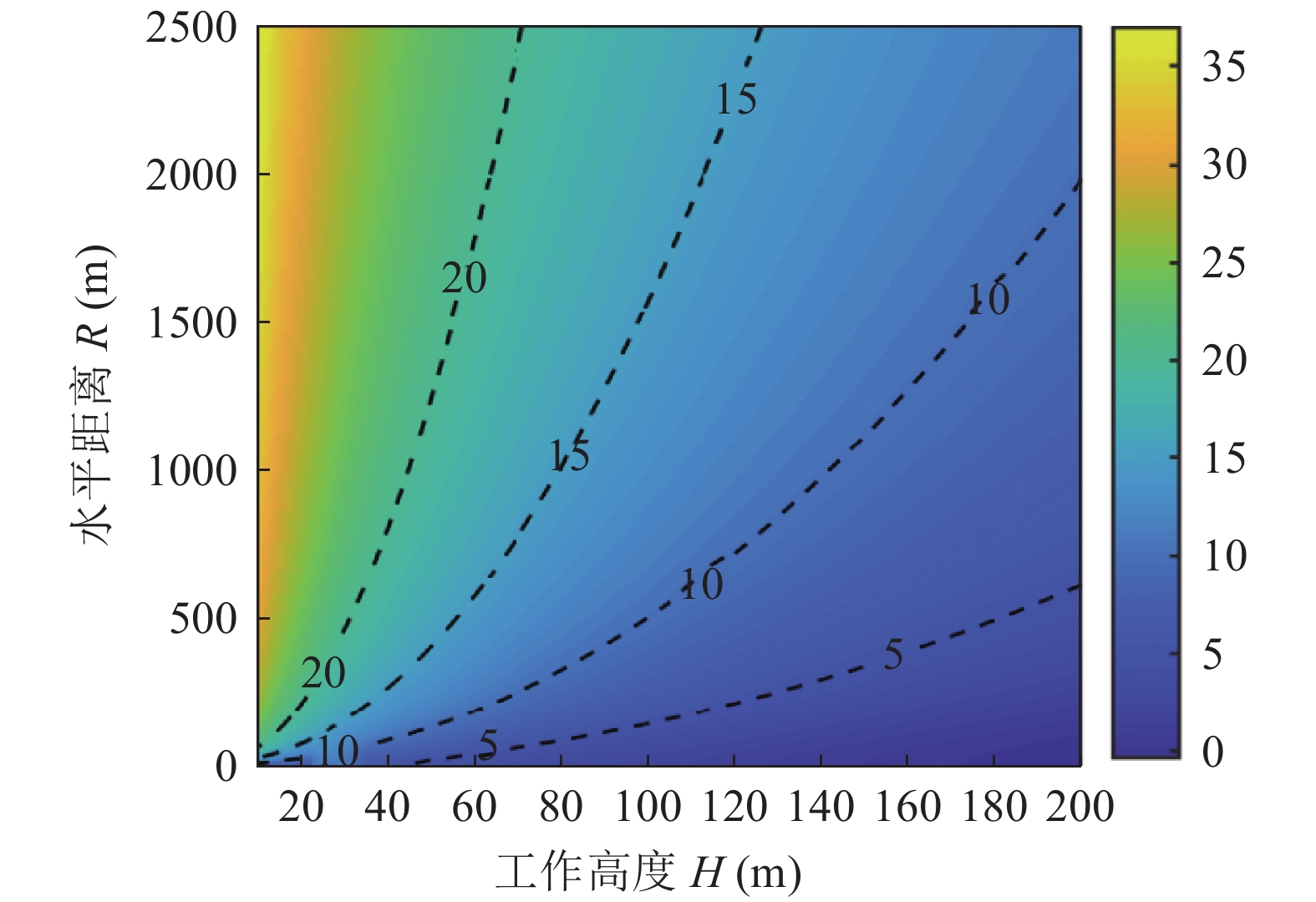
表 2 图14中各算法估计结果TSECBF 解卷积 1范数正则化 L1TV TSE 10918 4403 4750 3085 表 3 图15中各算法估计结果TSECBF 解卷积 1范数正则化 L1TV TSE 2251 600 615 506 对于图1所示的探测场景, 在1.2节对该场景下回波信混比大小进行了推导, 这里结合具体参数对不同高度与不同水平距离下目标回波信混比进行计算。使用的计算参数如下: 发射扇面开角为60°, 信号脉宽为50 ms, 目标强度TS为20 dB, 海底底质假设为砂砾沉积物, 相应的兰伯特常数
10\lg \mu = - 19 , 计算结果如图16 所示。可以看出, 对于同一水平距离, 随着工作高度的降低, 声波的掠射角会逐渐降低, 根据兰伯特散射模型, 此时海底混响减弱, 信号的信混比相应增加。所以通过适当降低探测高度, 使探测区域处于小掠射角下, 可以有效提升信混比。根据图16, 当探测高度选取为50 m的时候, 大部分水平区域的信混比都大于10 dB, 在这种条件下, 本文算法均可以得到较为理想的探测结果。4. 结论
针对海底目标探测当中, 常规波束形成方位分辨能力较低, 而一些高分辨的方位分辨算法对方位扩展目标估计结果不理想的问题, 提出了混合1范数与全变分正则化算法。结合海底探测场景, 针对不同类型的目标, 在不同的信混比下将本文算法与其他算法进行了对比, 结果显示, 所提算法估计结果中目标边界清晰, 对比度更高, 且与设置目标之间具备最低的平方误差。因此本文算法能够提升对方位扩展目标的探测性能。此外, 以二值化后的TSE作为评价指标, 讨论了迭代次数与算法参数对算法性能的影响。其中加权参数
{\alpha _1} 与{\alpha _2} 控制着1范数约束与全变分约束所占比例大小,{\alpha _1} 越大结果分辨率越高, 目标内部平滑性越低, 反之亦然; 而惩罚因子\xi 则控制整体约束的大小, 对于混响背景, 特别是低信混比下, 需要更大的\xi 才能获得理想的结果。最后, 对海底探测场景下的目标回波信混比进行了分析, 在探测高度较低时, 目标回波信混比较高, 此时算法能够达到理想的效果。 -
约束分裂增广拉格朗日收缩算法(CSALSA) 输入: {\boldsymbol{y}}, \quad \xi > 0, \quad {\boldsymbol{x}}^{(0)}= \mathbf{0}, \quad \lambda^{(0)}=\mathbf{0},\quad \alpha_1 > 0, \quad \alpha_2 > 0, \quad \alpha_1+\alpha_2=1 {\rm{for}}\; k = 0:K - 1 {{\boldsymbol{s}}^{(k + 1)}} = {({{\boldsymbol{G}}^{\rm{H}}}{\boldsymbol{G}})^{ - 1}}{{\boldsymbol{G}}^{\rm{H}}}({{\boldsymbol{x}}^{(k)}} + {{\boldsymbol{\lambda}} ^{(k)}}), {\boldsymbol{x}}_0^{(k + 1)} = \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{y}} + \sigma \dfrac{{{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){{\boldsymbol{s}}^{(k + 1)}} -{\boldsymbol{ \lambda}} _0^{(k)} - {\boldsymbol{y}}}}{{{{\left\| {{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _0^{(k)} - y} \right\|}_2}}}{\text{, }}\quad\quad{{\left\| {{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _0^{(k)} - {\boldsymbol{y}}} \right\|}_2} > \sigma, } \\ {{\boldsymbol{A}}(\overline {\boldsymbol{\theta}} ){{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _0^{(k)}{\text{, }}\quad\quad\quad\qquad\qquad{{\left\| {{\boldsymbol{A}}(\overline \theta ){{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _0^{(k)} - y} \right\|}_2} \leqslant \sigma, } \end{array}} \right. {\boldsymbol{x}}_1^{(k + 1)} = {\rm{sof}}{{\rm{t}}_{\tfrac{{{\alpha _1}}}{\xi }}}\left(\left| {{{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _1^{(k)}} \right|\right), {\boldsymbol{x}}_2^{(k + 1)} = {{\rm{C}}_{\frac{{{\alpha _2}}}{\xi }}}\left(\left| {{{\boldsymbol{s}}^{(k + 1)}} - {\boldsymbol{\lambda}} _2^{(k)}} \right|\right), {{\boldsymbol{\lambda}} ^{(k + 1)}} = {{\boldsymbol{\lambda}} ^{(k)}} + {{\boldsymbol{x}}^{(k + 1)}} - {\boldsymbol{G}}{{\boldsymbol{s}}^{(k + 1)}} {\rm{end}} 输出: {{\boldsymbol{s}}^{(K)}} 表 1 图11中各算法估计结果TSE
CBF 解卷积 1范数正则化 L1TV TSE 21648 10115 10863 7781 表 2 图14中各算法估计结果TSE
CBF 解卷积 1范数正则化 L1TV TSE 10918 4403 4750 3085 表 3 图15中各算法估计结果TSE
CBF 解卷积 1范数正则化 L1TV TSE 2251 600 615 506 -
[1] Urick R J. 水声原理. 第3版. 洪申, 译. 哈尔滨: 哈尔滨船舶工程学院出版社, 1990: 190—224 [2] Jackson D R, Baird A M, Crisp J J et al. High-frequency bottom backscatter measurement in shallow water. J. Acoust. Soc. Am., 1986; 80(4): 1188—1199 DOI: 10.1121/1.393809
[3] Stanic S, Briggs K B, Fleischer P et al. Shallow-water high-frequency bottom scattering off Panama City, Florida. J. Acoust. Soc. Am., 1988; 83(6): 2134—2144 DOI: 10.1121/1.396341
[4] Stanic S, Briggs K B, Fleischer P et al. High-frequency acoustic backscattering from a coarse shell ocean bottom. J. Acoust. Soc. Am., 1989; 85(1): 125—136 DOI: 10.1121/1.397720
[5] McKinney C M, Anderson C D. Measurements of backscattering of sound from the ocean bottom. J. Acoust. Soc. Am., 1964; 36(1): 158—163 DOI: 10.1121/1.1918927
[6] Jackson D R, Winebrenner D P, Ishimaru A. Application of the composite roughness model to high-frequency bottom backscattering. J. Acoust. Soc. Am., 1986; 79(5): 1410—1422 DOI: 10.1121/1.393669
[7] van Veen B D, Buckley K M. Beamforming: a versatile approach to spatial filtering. IEEE ASSP Mag., 1988; 5(2): 4—24 DOI: 10.1109/53.665
[8] Capon J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE, 1969; 57(8): 1408—1418 DOI: 10.1109/PROC.1969.7278
[9] Schmidt R, Schmidt R O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag., 1986; 34(3): 276—280 DOI: 10.1109/TAP.1986.1143830
[10] Yang T C. Deconvolved conventional beamforming for a horizontal line array. IEEE J. Oceanic Eng., 2017; 43(1): 160—172 DOI: 10.1109/JOE.2017.2680818
[11] 王朋, 迟骋, 纪永强, 等. 二维解卷积波束形成水下高分辨三维声成像. 声学学报, 2019; 44(4): 613—625 DOI: 10.15949/j.cnki.0371-0025.2019.04.022 [12] Malioutov D, Cetin M, Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process., 2005; 53(8): 3010—3022 DOI: 10.1109/TSP.2005.850882
[13] Rudin L I, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Phys. D, 1992; 60(1-4): 259—268 DOI: 10.1016/0167-2789(92)90242-F
[14] Güven H E, Güngör A, Çetin M. An augmented Lagrangian method for complex-valued compressed SAR imaging. IEEE Trans. Comput. Imaging, 2016; 2(3): 235—250 DOI: 10.1109/TCI.2016.2580498
[15] Wang S, Chi C, Wang P et al. Feature-enhanced beamforming for underwater 3-D acoustic imaging. IEEE J. Oceanic Eng., 2023; 48(2): 401—415 DOI: 10.1109/JOE.2022.3214326
[16] Chi C, Li Z, Li Q. Ultrawideband underwater real-time 3-D acoustical imaging with ultrasparse arrays. IEEE J. Oceanic Eng., 2017; 42(1): 97—108 DOI: 10.1109/JOE.2016.2549838
[17] Afonso M V, Bioucas-Dias J M, Figueiredo M A T. An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems. IEEE Trans. Image Process., 2011; 20(3): 681—695 DOI: 10.1109/TIP.2010.2076294
[18] Foucart S, Rauhut H. A mathematical introduction to compressive sensing. New York : Springer, 2013
[19] Boyd S, Parikh N, Chu E et al. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn., 2010; 3(1): 1—122 DOI: 10.1561/2200000016
[20] Wright S J, Nowak R D, Figueiredo M. Sparse reconstruction by separable approximation. IEEE Trans. Signal Process., 2009; 57(7): 2479—2493 DOI: 10.1109/TSP.2009.2016892
[21] Chambolle A. An algorithm for total variation minimization and applications. J. Math. Imaging Vision, 2004; 20(1—2): 89—97 DOI: 10.1023/B:JMIV.0000011325.36760.1e
[22] Lei Z, Yang K, Zhang Q et al. Two dimensional TV-L1 regularization for underwater acoustic source tracking. IEEE OCEANS, IEEE, Shanghai, China, 2016
[23] Palmese M, Trucco A. Acoustic imaging of underwater embedded objects: Signal simulation for three-dimensional sonar instrumentation. IEEE Trans. Instrum. Meas., 2006; 55(4): 1339—1347 DOI: 10.1109/TIM.2006.876402
[24] Gensane M. A statistical study of acoustic signals backscattered from the sea bottom. IEEE J. Oceanic Eng., 1989; 14(1): 84—93 DOI: 10.1109/48.16818
[25] 张小利, 李雄飞, 李军. 融合图像质量评价指标的相关性分析及性能评估. 自动化学报, 2014; 40(2): 306—315 DOI: 10.3724/SP.J.1004.2014.00306 [26] 万新光, 李岩, 姜中林. 计算机图象分割及其算法. 哈尔滨科学技术大学学报, 1991; 15(3): 59—65 -
期刊类型引用(1)
1. 杨泽慧,聂炜航,程高峰,吴姚振,徐及,赵庆卫,颜永红. 全变分约束的解卷积常规波束形成方位谱估计算法. 声学学报. 2025(01): 68-76 .  本站查看
本站查看
其他类型引用(0)



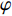
 下载:
下载: