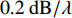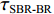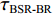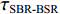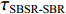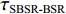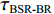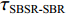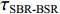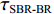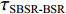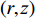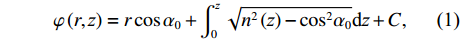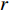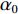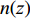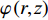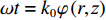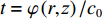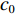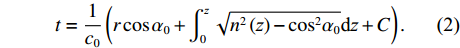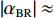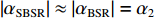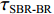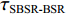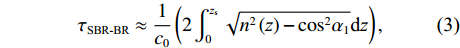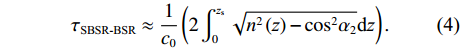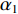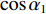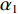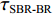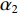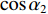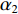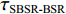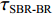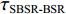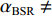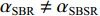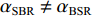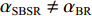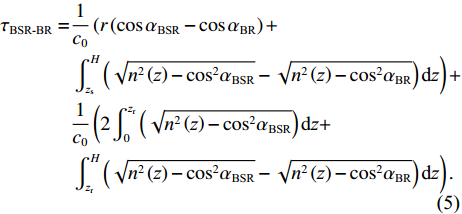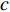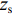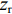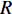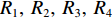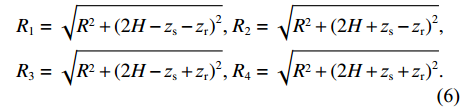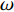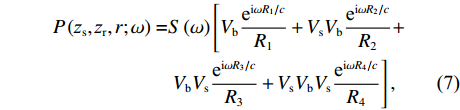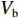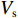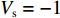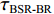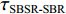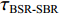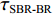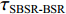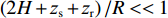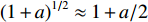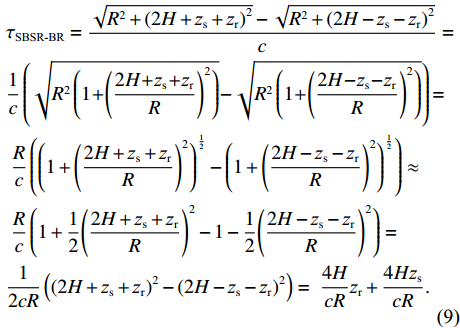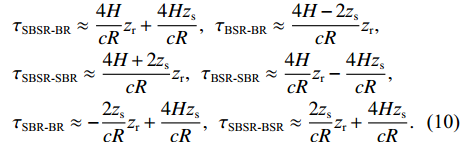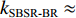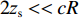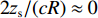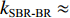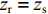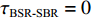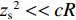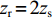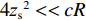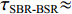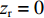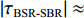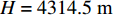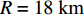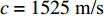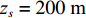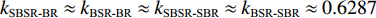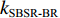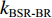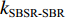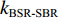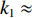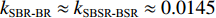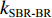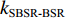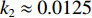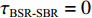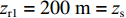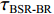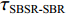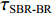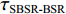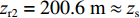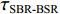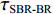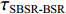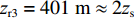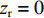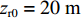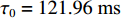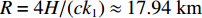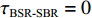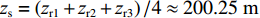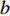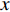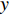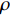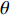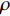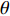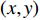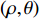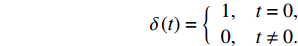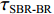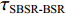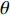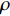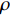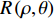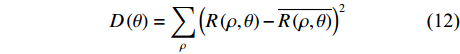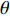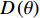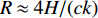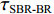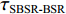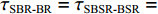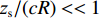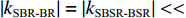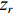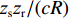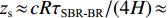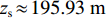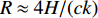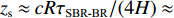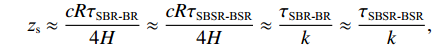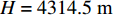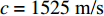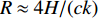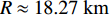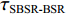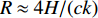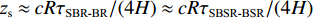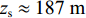深海海底声反射区多途时延差分析与近海面声源定位

徐嘉璘; 郭良浩; 任云

doi:10.15949/j.cnki.0371-0025.2023.04.013

深海海底声反射区多途时延差分析与近海面声源定位

徐嘉璘^{1, 2,},
郭良浩^1, ,,
任云¹

1.
中国科学院声学研究所声场声信息国家重点实验室　北京　100190
2.
中国科学院大学　北京　100049

基金项目: 国家自然科学基金项目(11874061)资助

详细信息

作者简介:
徐嘉璘, xujialin@mail.ioa.ac.cn

通讯作者:
郭良浩, glh2002@mail.ioa.ac.cn

PACS:
- 43.30 (水声学)
- 43.60 (声学信号处理)
计量
- 文章访问数: 344
- HTML全文浏览量: 31
- PDF下载量: 69
出版历程
- 收稿日期: 2022-10-15
- 修回日期: 2023-01-01
- 网络出版日期: 2023-07-12
- 刊出日期: 2023-07-10

Analysis of multipath time delay difference in deep ocean bottom bounce area and its application in near-surface target location

XU Jialin^{1, 2,},
GUO Lianghao^1, ,,
REN Yun¹

1.
State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences　Beijing　100190
2.
University of Chinese Academy of Sciences　Beijing　100049

摘要

摘要:
深海海底反射声工作方式下的声场主要由4条一次海底反射声线路径构成。根据4条声线路径到达接收点的时间不同, 可以得到6个不同的声线到达时延差值, 当声源位于近海面时, 6条声线路径的时延差曲线随接收深度近似呈线性变化。本文基于虚源理论推导了海底声反射区的多途到达时延结构, 给出了6条声线路径的时延差曲线随接收深度变化的近似表达式, 通过分析时延差曲线与声源水平距离和深度之间的关系, 提出了一种利用多途时延差估计深海海底声反射区近海面声源距离与深度的方法, 仿真实验与影响因素分析验证了该原理的正确性。南海实验结果表明, 当收发距离在10~33 km时, 距离估计结果和深度估计结果都同实际声源距离和深度吻合较好, 估计误差不超过15%, 验证了该方法的有效性。
- 海底声反射区 /
- 多途时延结构 /
- 无源定位 /
- 大接收深度
Abstract:
The bottom bounce areas in the first shadow zone in deep ocean are mostly contributed by four eigenrays including bottom-reflected path, surface-bottom-reflected path, bottom-surface-reflected path and surface-bottom-surface-reflected path, all of which arrive at different time with different time delay. On the basis of the time delay of four eigenrays, six arrival delay differences in deep ocean bottom bounce area can be obtained. As for a near-surface target source in deep ocean, six delay difference curves of eigenrays change approximately linearly with receiving depth. In this paper, the multipath arrival time delay structure of the bottom bounce areas in deep ocean is derived by the virtual source theory, and the approximate formulae of the time delay difference curves varying with the receiving depth are deduced. By analyzing the relationship between the time delay curves and the source range and depth, a method for source ranging and depth estimation in deep ocean bottom bounce area is proposed. The approach is demonstrated valid by the simulated data. Experimental results in the South China Sea show that when the transmitting and receiving distance is between 10 km and 30 km, the range and depth estimation results are in good agreement with the actual explosion range and depth, and the estimation error is less than 12%, which verifies the effectiveness of this method.
- Bottom bounce area /
- Multipath delay structure /
- Passive localization /
- Large receiving depth

HTML全文

引言

在国家建设海洋强国政策的大力驱动下，对于水下目标定位技术的需求越来越迫切^[1]。伴随科技的不断发展, 我国对水下目标的定位逐渐从近岸走向远洋, 从浅水走向深海。目前, 深海目标定位已成为未来地球科学领域的重要发展方向和可能取得重大突破的领域之一。

匹配场定位^[2-4]作为深海无源定位中最常用的定位方法, 最早的实验研究可追溯至20世纪80年代, Fizell等^[5]使用一个垂直线列阵成功定位到260 km远处的低频声源信号; Transfer等^[6]在太平洋东北部进行了深海匹配场定位实验, 结果表明该方法在距离估计上能取得较好的效果, 而在深度估计上存在较大模糊; Westwood^[7]利用宽带频间相关匹配场处理, 成功实现了对墨西哥湾4500 m 深海中43 km内声源的定位, 实验结果表明增加信号带宽可以提高定位精度; 周士弘等^[8]将快速而精确的WKBZ简正波方法用于计算拷贝声场, 利用实验数据验证了垂直短阵实现深海匹配场定位的可能性。尽管有诸多实验成功验证了匹配场处理在深海无源定位中的有效性, 但是匹配场方法对环境敏感性高的问题一直没有得到很好的解决^[9-13], 使得匹配场方法在深海无源定位中始终没有突破性的进展。

由于可以利用接收阵列获得较为明显的多途信号到达结构, 近年来学者逐渐将研究的重心放在了基于多途时延和多途到达角的无源定位方法上^[14-16]。Li等^[17]研究了深海可靠声路径环境下的声线到达结构, 通过匹配直达声和海面反射声的时延差实现了目标测距。Duan等^[18]分析了可靠声路径条件下的移动声源定位方法, 利用自相关函数提取直达声和海面反射声的时延差实现了对运动目标的无源定位。Lei等^[19]利用不同深度的两个水听器的时延互相关匹配, 实现了深海目标的距离估计和深度估计。吴俊楠等^[20]研究了拖曳水平线列阵在深海直达声区对目标检测时的方位分裂现象, 并利用直达声线和海底反射声线所造成的目标方位角差异来实现直达声区声源距离的估计。孙梅等^[21]根据矢量水听器接收到的声信号, 利用水平振速和垂直振速的能量差实现了近水面声源的距离估计。高飞等^[22]研究了单水听器多途声到达时间差, 利用扩展卡尔曼滤波(EKF)算法对深海浅层移动声源进行定位。王梦圆等^[23-24]根据南海实验数据对海底附近脉冲多途传播特性进行分析, 利用直达波和海底−海面反射波的到达时间差实现了对深海直达声区水下声源的距离估计, 并通过直达波与海面反射波到达时间差随声源深度的变化特性提出了一种距离深度联合的目标定位方法。谢亮等^[25]通过分析典型深海环境中脉冲信号的到达结构特征, 提出了一种匹配到达信号簇特征参数的水下脉冲信号目标定位方法。刘炎堃等^[26]利用深海直达波与海面反射波到达时延与位置之间的关系, 预先构建出候选运动路径, 通过使用候选路径对目标运动轨迹进行模拟, 实现了对直达声区目标的深度估计。

已有的利用深海声场多途到达结构进行声源定位的方法中, 对可靠声路径和直达声区的声传播特性研究较多, 对海底声反射区和影区的声场特性研究涉及较少, 尤其是针对不同接收深度下海底声反射区多途到达结构的研究尚不充分, 相关定位方法对环境敏感性较高。本文主要研究深海海底声反射区近海面声源多途到达结构的变化规律, 基于虚源理论推导了6条时延差曲线随接收深度变化的近似表达式, 通过分析时延差曲线与声源水平距离和深度之间的关系, 提出了一种利用多途时延差估计深海海底声反射区近海面声源距离与深度的方法, 并开展仿真实验与影响因素分析验证了方法在原理上的正确性, 最后利用实际海试数据对该方法的可行性和有效性进行了验证。

1. 海底声反射区多途时延到达结构分析

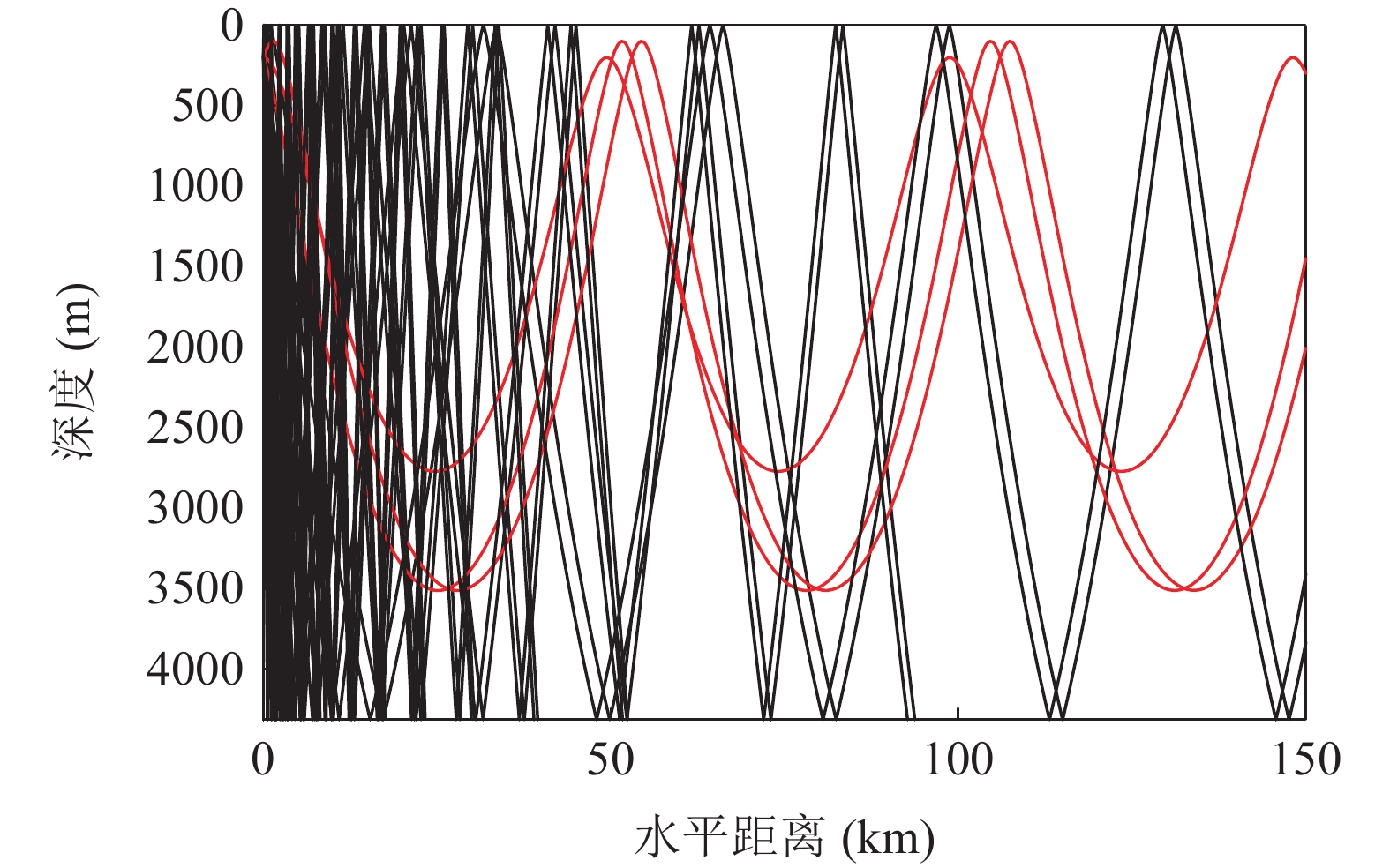
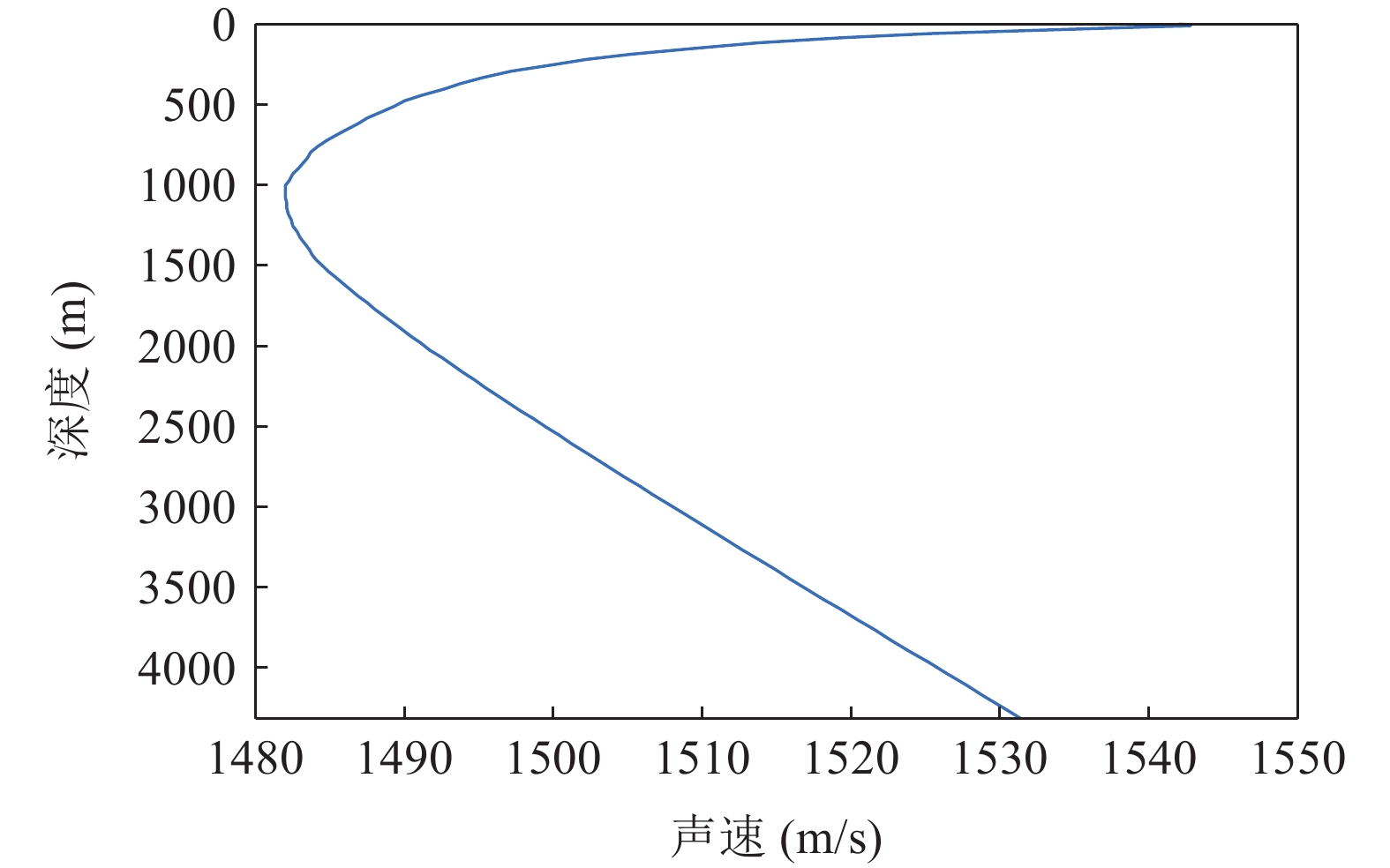
当接收器与声源都接近海面时, 根据收发距离的不同, 可以将典型深海声场在空间上划分为直达声区、影区和会聚区三大区域。直达声区是指声线未经海底反射或未经海底附近反转的声场区域, 影区是指直达声线和反转声线无法到达的声场区域, 会聚区是指反转声线在海面附近形成的高声强焦散声场区域。图1和图2分别为典型深海声道的垂直声速剖面图和声线传播图, 其中海深为4314.5 m, 声源深度为200 m, 声道轴深度为1000 m。

图 1 深海典型垂直声速剖面

下载: 全尺寸图片幻灯片

图 2 深海典型声线传播图

下载: 全尺寸图片幻灯片

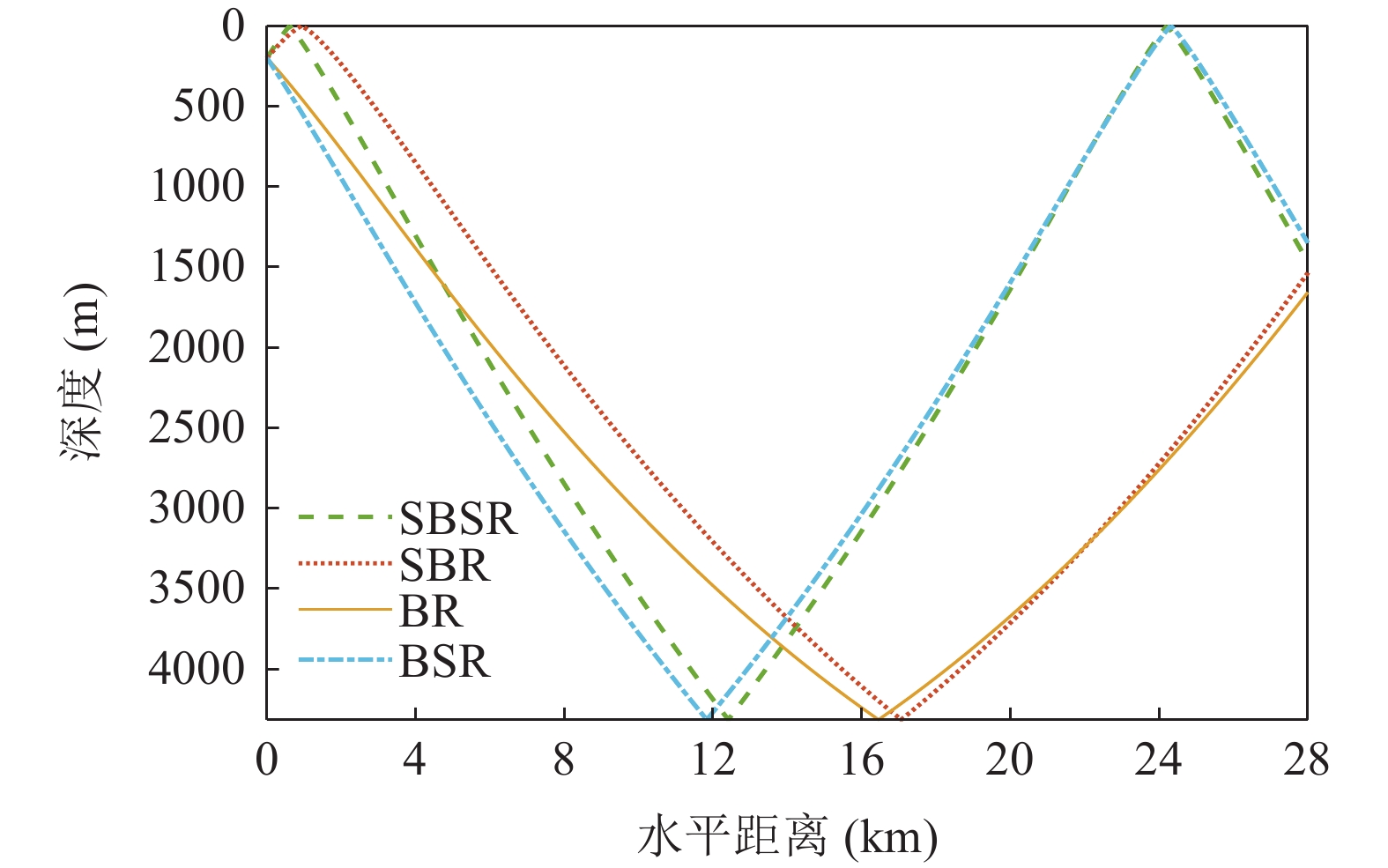
海底声反射区是指主要由海底海面反射声线构成的声场区域, 是深海影区的重要组成部分。本文所要关注的海底声反射区是指第一会聚区以近距离内的海底声反射区, 其主要是由一次海底反射声线构成, 是第一影区内的重要组成部分, 它主要由4条声线传播路径构成, 如图3所示, 分别是海底声反射声线(BR)、海面−海底声反射声线(SBR)、海底−海面声反射声线(BSR)、海面−海底−海面声反射声线(SBSR)。

图 3 深海海底声反射区本征声线结构图

下载: 全尺寸图片幻灯片

根据海底声反射区4条声线路径到达接收点的时间, 可以得到6个不同的声线到达时延差。时延差定义为各路径声线的传播时间之差, 其物理意义为各声线的声程差所产生的时延。时延差中蕴含着声源位置信息, 可以通过提取6个时延差中的信息量对海底声反射区声源进行距离估计和深度估计。首先通过Bellhop计算模型进行仿真分析。

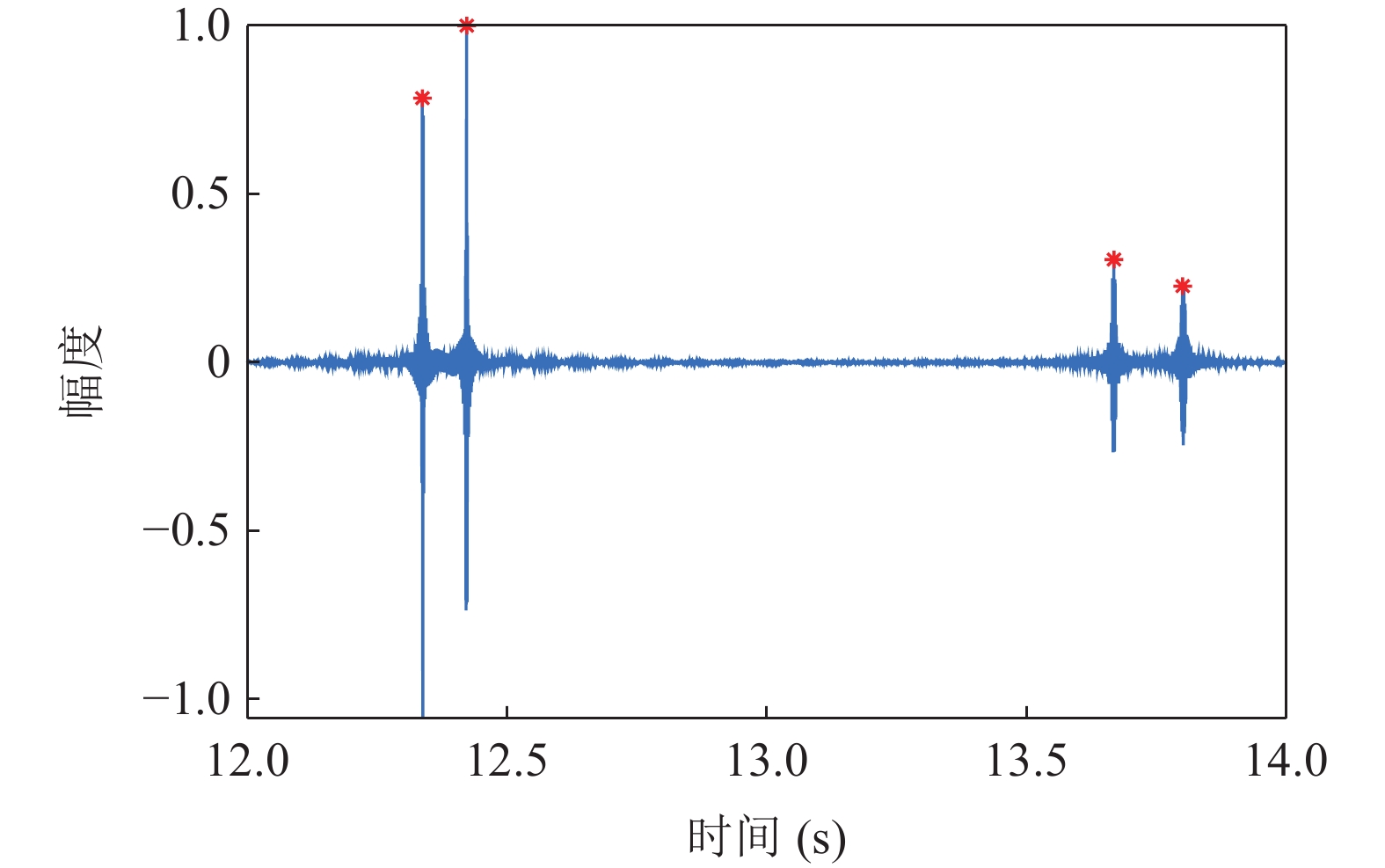
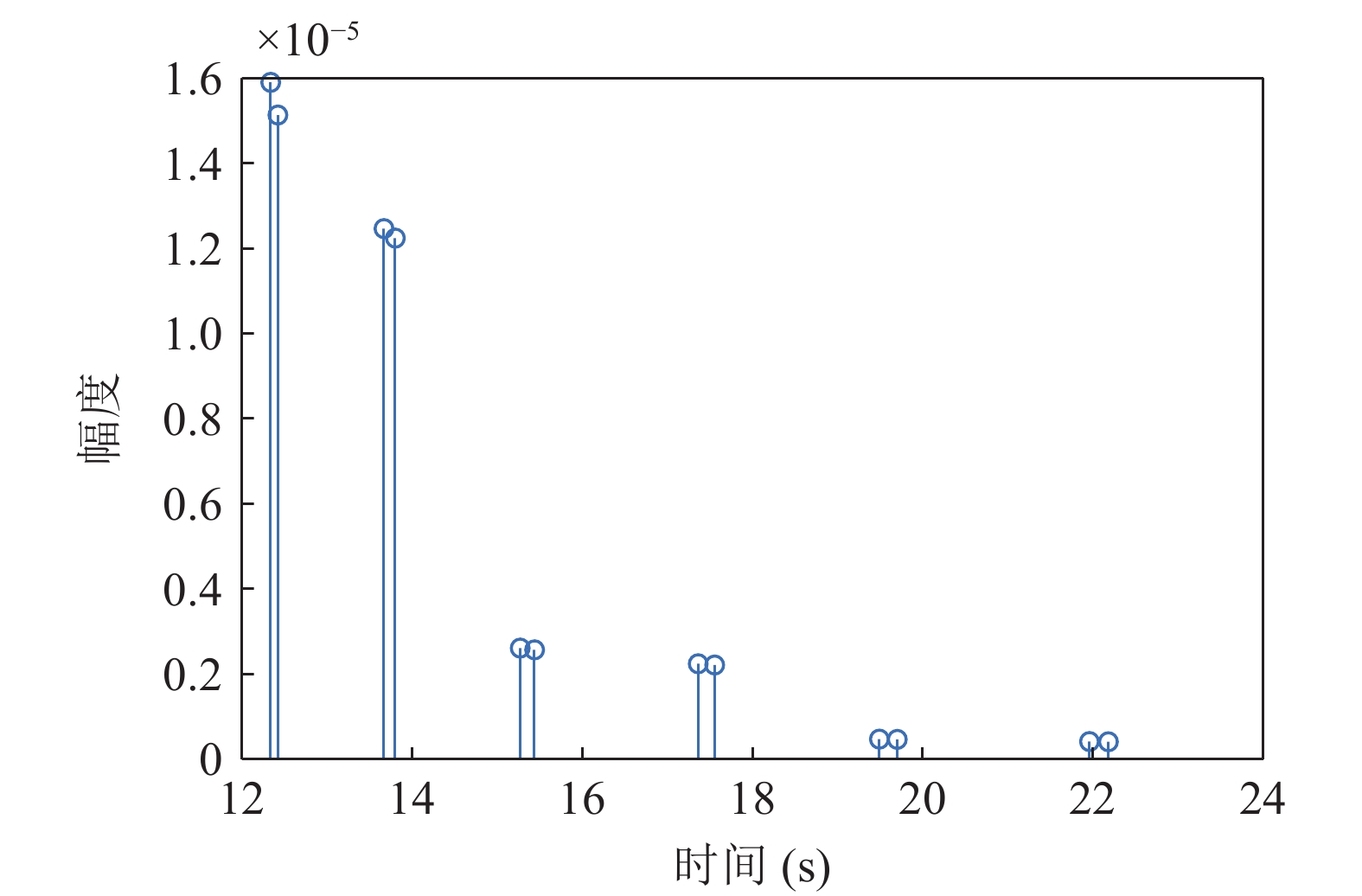
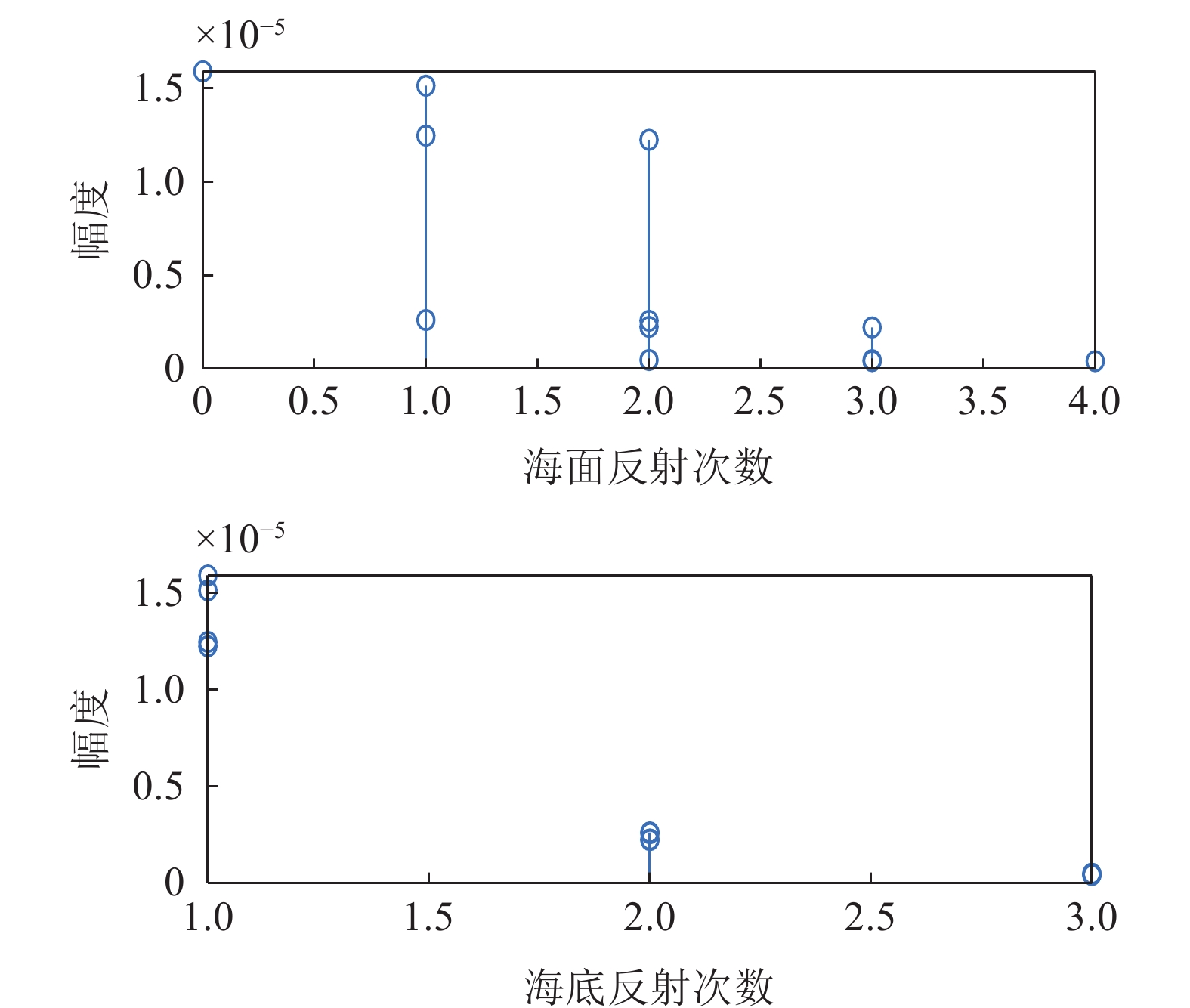
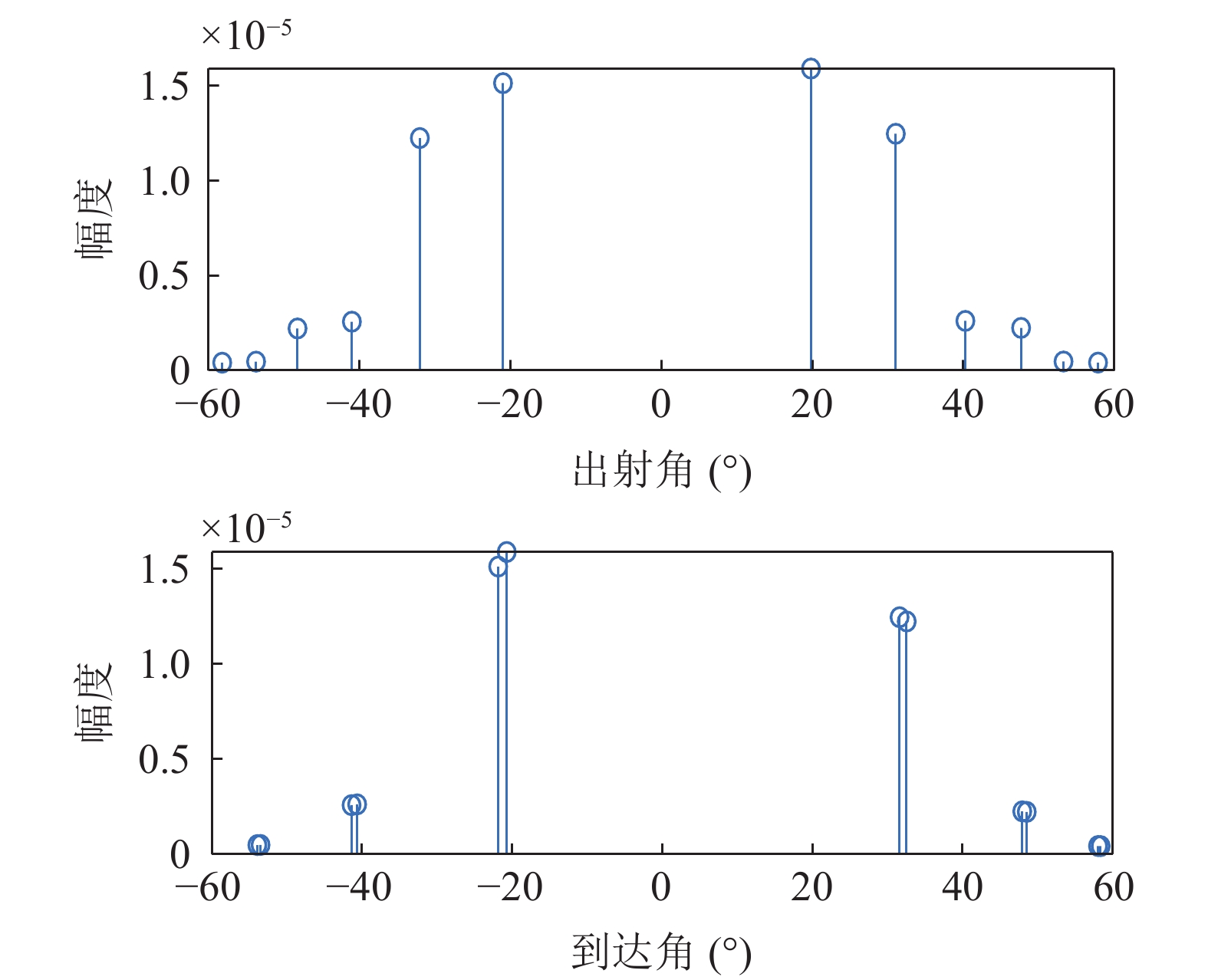
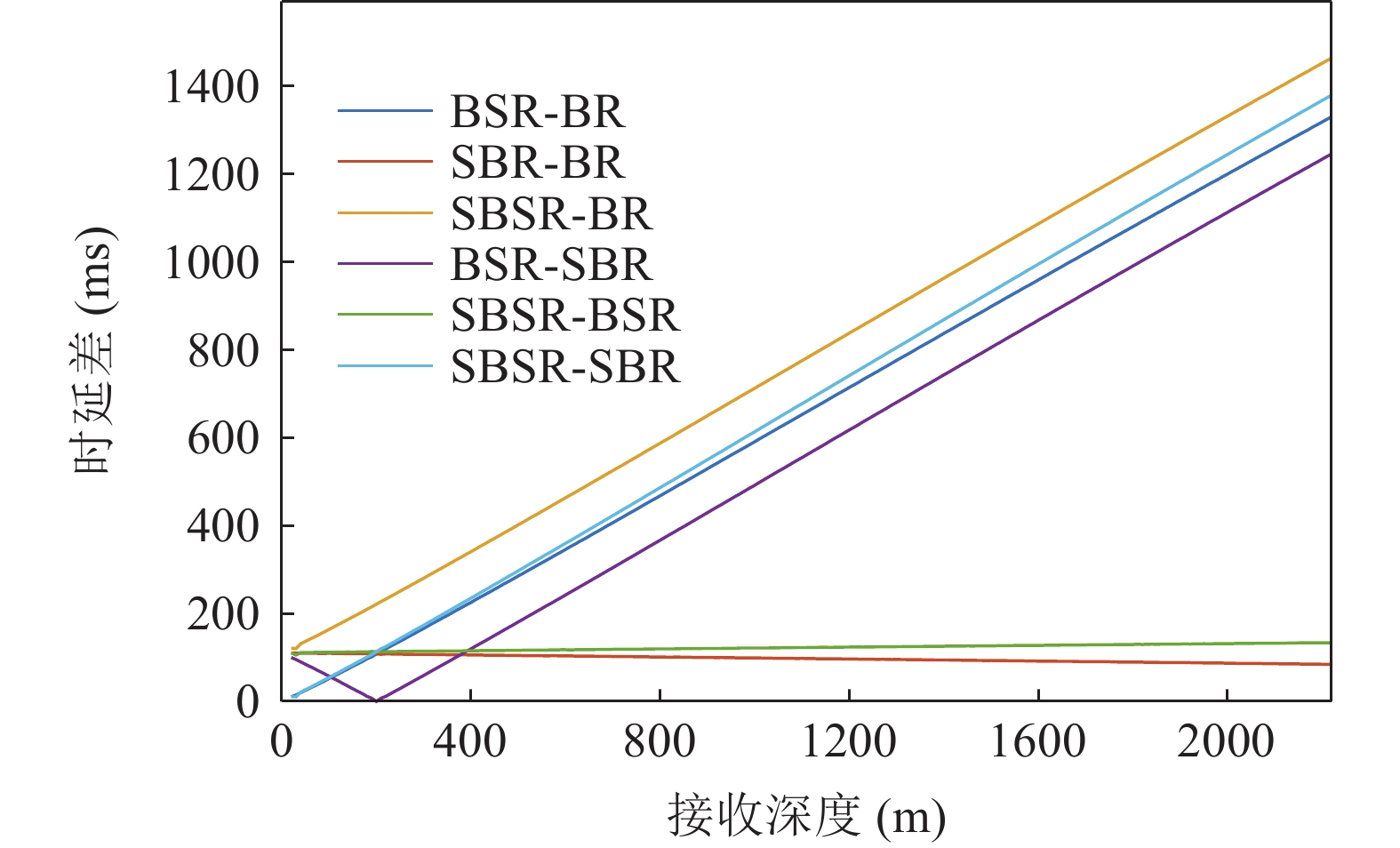
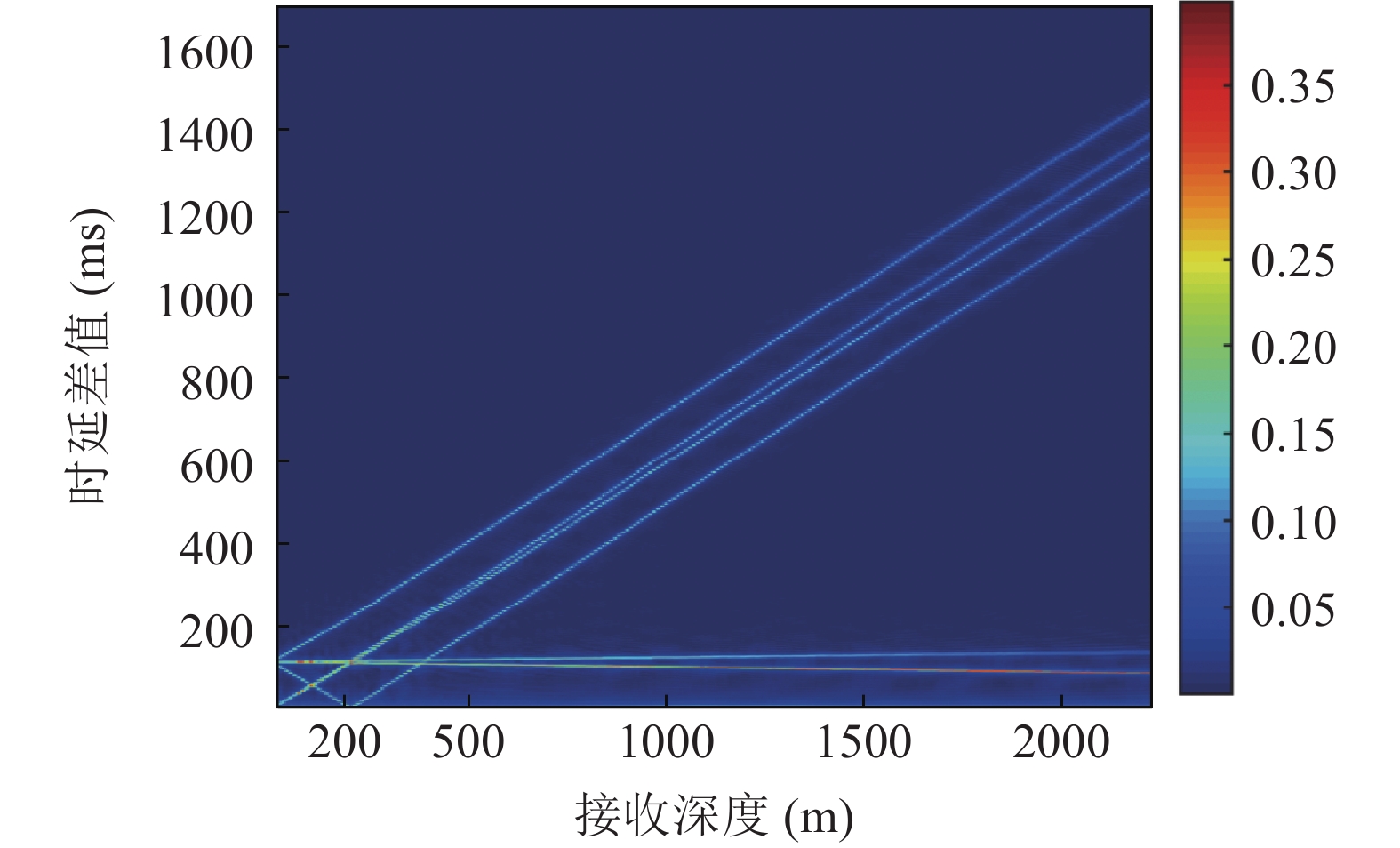
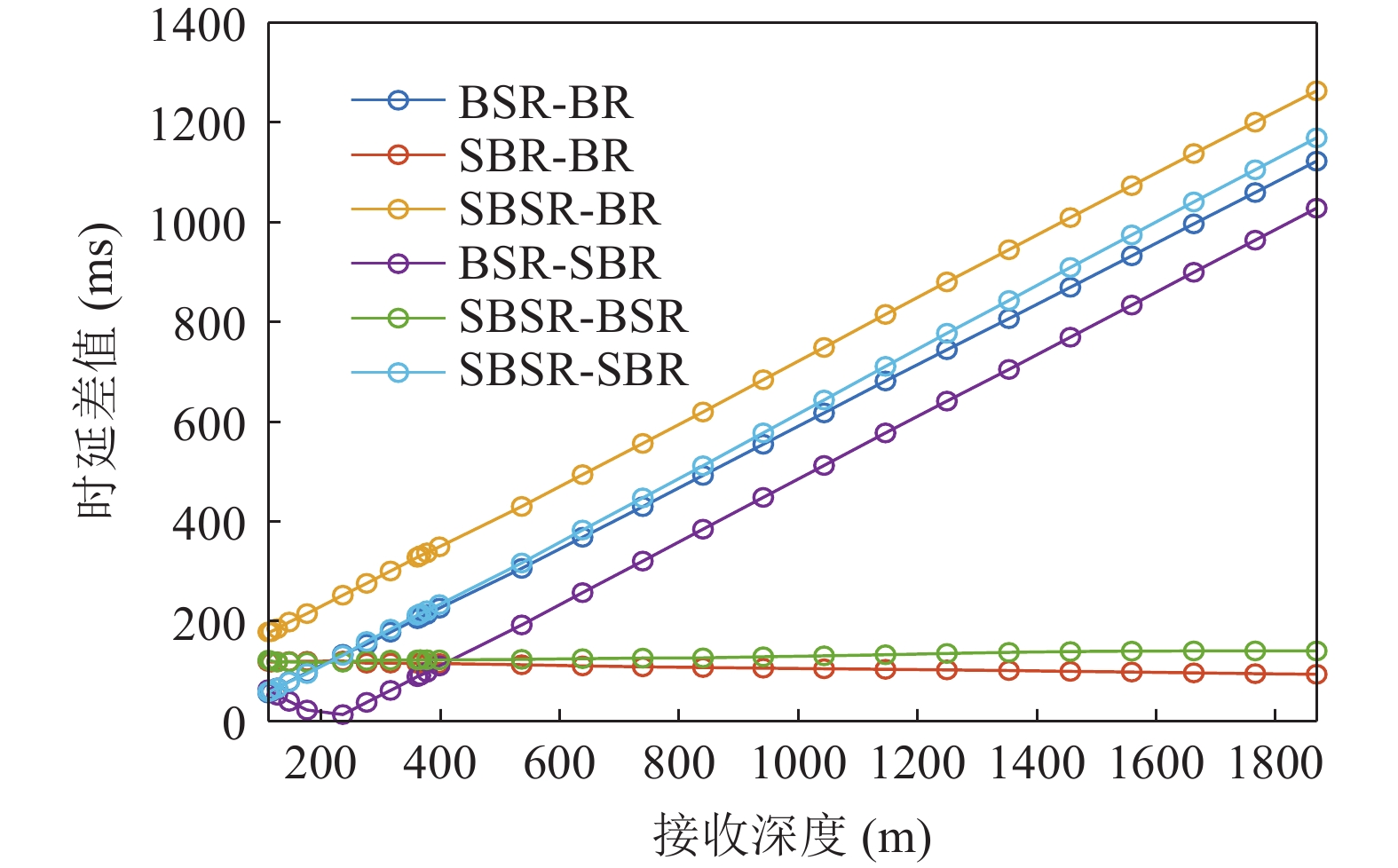
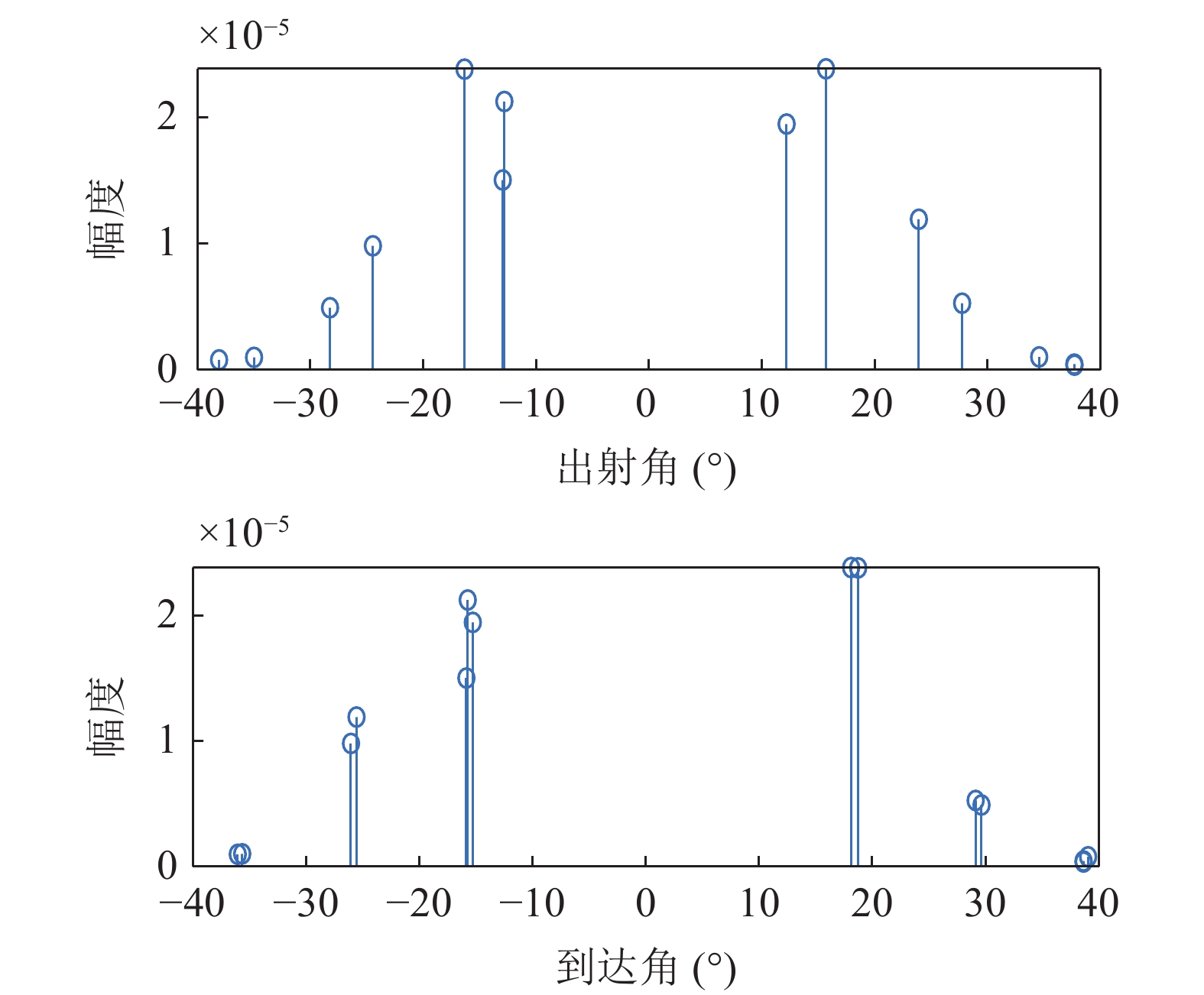
仿真环境为4314.5 m深海, 水中垂直声速剖面如图1所示, 声道轴深度为1000 m。海底为半无限空间, 海底声速为1550 m/s, 海底密度为1.6 g/cm³, 吸收系数为 $0.2\;{{ {\rm{dB}}/\lambda }}$ 。垂直阵阵长为2200 m, 阵元间距为10 m, 均匀分布在海面以下20~2220 m的深度上。声源深度为200 m, 收发距离为18 km。声源发射LFM信号, 信号频率为350~750 Hz。图4给出了不同接收深度经过脉冲压缩的时域信号。图5—图8分别给出了接收深度为2220 m时经过脉冲压缩的时域接收信号、声线时间到达结构、声线反射次数以及声线出射角和到达角。从图中可以看出, 不同接收深度的到达时间结构主要由4个到达时间簇构成, 分别对应海底声反射区4条一次海底反射声线的到达时间。当接收深度小于声源深度时, 到达接收阵元的声线路径按时间先后顺序分别为: 海底反射声线、海底−海面反射声线、海面−海底反射声线和海面−海底−海面反射声线。当接收深度大于声源深度时, 到达接收阵元的声线路径按时间先后顺序分别为: 海底反射声线、海面−海底反射声线、海底−海面反射声线和海面−海底−海面反射声线。当接收深度等于声源深度时, 由于海底−海面反射声线和海面−海底反射声线的到达时间相等, 此时到达该接收深度的时间结构主要由3个时间簇构成, 对应海底反射声线、海底−海面反射声线 (海面−海底反射声线)和海面−海底−海面反射声线的到达时间。随着接收深度的增加, 海底反射声线和海面−海底反射声线的到达时间越来越短, 而海底−海面反射声线和海面−海底−海面反射声线的到达时间越来越长。为表述方便, 下文将4条声线路径分别用BR、BSR、SBR和SBSR代称。

图 4 不同阵元经过脉冲压缩的时域接收信号

下载: 全尺寸图片幻灯片

图 5 接收深度2220 m时经过脉冲压缩的时域接收信号

下载: 全尺寸图片幻灯片

图 6 接收深度2220 m时的声线到达时间结构

下载: 全尺寸图片幻灯片

图 7 接收深度2220 m时的声线反射次数

下载: 全尺寸图片幻灯片

图 8 接收深度2220 m时的声线出射角和到达角

下载: 全尺寸图片幻灯片

将不同阵元接收信号的4个时间簇峰值提取出来, 两两组合, 可以得到6个不同的时延差值, 分别为 ${\tau _{{\text{SBR-BR}}}}$ , ${\tau _{{\text{BSR-BR}}}}$ , ${\tau _{{\text{SBSR-BR}}}}$ , ${\tau _{{\text{SBR-BSR}}}}$ , ${\tau _{{\text{SBSR-SBR}}}}$ , ${\tau _{{\text{SBSR-BSR}}}}$ 。图9给出了6个时延差值随接收深度的变化曲线。从图中可以看出, 随着接收深度的增加, ${\tau _{{\text{BSR-BR}}}}$ , ${\tau _{{\text{SBSR-BR}}}}$ , ${\tau _{{\text{SBSR-SBR}}}}$ 逐渐增大, ${\tau _{{\text{SBR-BSR}}}}$ 先减小后增大, ${\tau _{{\text{SBR-BR}}}}$ 和 ${\tau _{{\text{SBSR-BSR}}}}$ 基本不变。

图 9 时延差值随接收深度的变化结果

下载: 全尺寸图片幻灯片

考虑声线位于 $\left( {r,\textit{z}} \right)$ 平面内, 海洋波导通常具有水平分层特性, 海水声速只与深度坐标 $\textit{z}$ 有关, 则射线声学模型中程函方程可以表示如下

$\varphi \left( {r,\textit{z}} \right) = r\cos {\alpha _0} + \int_0^\textit{z} {\sqrt {{n^2}\left( \textit{z} \right) - {{\cos }^2}{\alpha _0}} {\text{d}}\textit{z} + C} ,$

(1)

其中, $r$ 为水平距离, ${\alpha _0}$ 为声线的出射掠射角, $n(\textit{z})$ 为折射率, $C$ 为积分常数。声线的传播时间可以表示为声线经过程函 $\varphi \left( {r,\textit{z}} \right)$ 所需要的时间, 根据 $\omega t = {k_0}\varphi \left( {r,\textit{z}} \right)$ 可得 $t = \varphi \left( {r,\textit{z}} \right)/{c_0}$ , ${c_0}$ 为声源处的海水声速, 则声线的传播时间表达式为

$t = \frac{1}{{{c_0}}}\left( {r\cos {\alpha _0} + \int_0^\textit{z} {\sqrt {{n^2}\left( \textit{z} \right) - {{\cos }^2}{\alpha _0}} {\text{d}}\textit{z} + C} } \right).$

(2)

表1给出了Bellhop模型计算的3个接收深度下声源信号对应的每条声线的出射掠射角。

表 1 不同接收深度对应的4条声线的出射掠射角

接收深度 (m)	${\alpha _{{\text{SBR}}}}$ (°)	${\alpha _{{\text{SBSR}}}}$ (°)	${\alpha _{{\text{BR}}}}$ (°)	${\alpha _{{\text{BSR}}}}$ (°)
200	−26.11	−27.2	24.99	26.12
1000	−24.07	−29.17	22.92	28.12
2000	−21.57	−31.51	20.36	30.52

下载: 导出CSV

| 显示表格

可以看出, 当声源深度较小时, 海底声反射区内无论接收深度的深浅, 声线都满足: $\left| {{\alpha _{\rm BR}}} \right| \approx \left| {{\alpha _{\rm SBR}}} \right| = {\alpha _1}$ , $\left| {{\alpha _{\rm SBSR}}} \right| \approx \left| {{\alpha _{\rm BSR}}} \right| = {\alpha _2}$ 。由于4条声线路径传播的水平距离相等, 因此当出射角近似相等时, 4条声线路径在距离维的声程差近似为0, 于是不同声线的时延差可以表示为不同声线在深度维的声程差所产生的时延, 则 ${\tau _{{\text{SBR-BR}}}}$ 和 ${\tau _{{\text{SBSR-BSR}}}}$ 可以写为

${\tau _{{\text{SBR-BR}}}} \approx \frac{1}{{{c_0}}}\left( {2\int_0^{{\textit{z}_{\rm s}}} {\sqrt {{n^2}\left( \textit{z} \right) - {{\cos }^2}{\alpha _1}} {\text{d}}\textit{z}} } \right),$

(3)

${\tau _{{\text{SBSR-BSR}}}} \approx \frac{1}{{{c_0}}}\left( {2\int_0^{{\textit{z}_{\rm s}}} {\sqrt {{n^2}\left( \textit{z} \right) - {{\cos }^2}{\alpha _2}} {\text{d}}\textit{z}} } \right).$

(4)

由式(3)和式(4)可以看出, 当声源深度和收发距离保持不变时, 由于 ${\alpha _1}$ 随着接收深度的增大而减小, $\cos {\alpha _1}$ 随 ${\alpha _1}$ 的变化幅度较小, 因此SBR路径与BR路径的时延差 ${\tau _{{\text{SBR-BR}}}}$ 随着接收深度的增大而缓慢减小; 由于 ${\alpha _2}$ 随着接收深度的增大而增大, $\cos {\alpha _2}$ 随 ${\alpha _2}$ 的变化幅度较小, 因此SBSR路径与BSR路径的时延差 ${\tau _{{\text{SBSR-BSR}}}}$ 随着接收深度的增大而缓慢增大, 这一规律符合图9中 ${\tau _{{\text{SBR-BR}}}}$ 和 ${\tau _{{\text{SBSR-BSR}}}}$ 曲线的变化情况。

从表1中还可以发现, 当接收深度较大时, ${\alpha _{{\text{BSR}}}} \ne {\alpha _{{\text{BR}}}}$ , ${\alpha _{{\text{SBR}}}} \ne {\alpha _{{\text{SBSR}}}}$ , ${\alpha _{{\text{SBR}}}} \ne {\alpha _{{\text{BSR}}}}$ , ${\alpha _{{\text{SBSR}}}} \ne {\alpha _{{\text{BR}}}}$ , 此时不同声线传播距离维的声程差所产生的时延不再近似为0, 不同声线路径的时延差由距离维声程差和深度维声程差所产生的时延共同组成, 以BSR路径和BR路径的时延差为例, 其时延差公式可以表示为

$\begin{split} {\tau _{{\text{BSR-BR}}}} =& \frac{1}{{{c_0}}}\left( r\left( {\cos {\alpha _{{\text{BSR}}}} - \cos {\alpha _{{\text{BR}}}}} \right) +\right. \\&\left.\int_{{\textit{z}_{\rm s}}}^H {\left( {\sqrt {{n^2}\left( \textit{z} \right) - {{\cos }^2}{\alpha _{{\text{BSR}}}}} - \sqrt {{n^2}\left( \textit{z} \right) - {{\cos }^2}{\alpha _{{\text{BR}}}}} } \right){\text{d}}\textit{z}} \right) + \\& \frac{1}{{{c_0}}}\left( 2\int_0^{{\textit{z}_{\rm r}}} \left( {\sqrt {{n^2}\left( \textit{z} \right) - {{\cos }^2}{\alpha _{{\text{BSR}}}}} } \right){\rm d}\textit{z} + \right.\\&\left. \int_{{\textit{z}_{\rm r}}}^H {\left( {\sqrt {{n^2}\left( \textit{z} \right) - {{\cos }^2}{\alpha _{{\text{BSR}}}}} - \sqrt {{n^2}\left( \textit{z} \right) - {{\cos }^2}{\alpha _{{\text{BR}}}}} } \right){\text{d}}\textit{z}} \right). \end{split}$

(5)

同理可得其他路径的时延差表达式。由于该表达式难以化简, 且随接收深度的变化情况不够直观, 因此试引入四元虚源法来简化模型。尽管四元虚源理论在原理上只适用于声源和接收器都接近海面的情况, 但通过观察图9中的曲线变化可以发现, 在一定的深度范围内, 6条声线路径的时延差曲线随接收深度近似呈线性变化, 即时延差的变化规律在接收深度变化时近似保持一致, 因此可以通过推导接收深度较浅时时延差随接收深度的变化规律来研究接收深度较深时时延差随接收深度的变化规律。

2. 定位原理及仿真研究

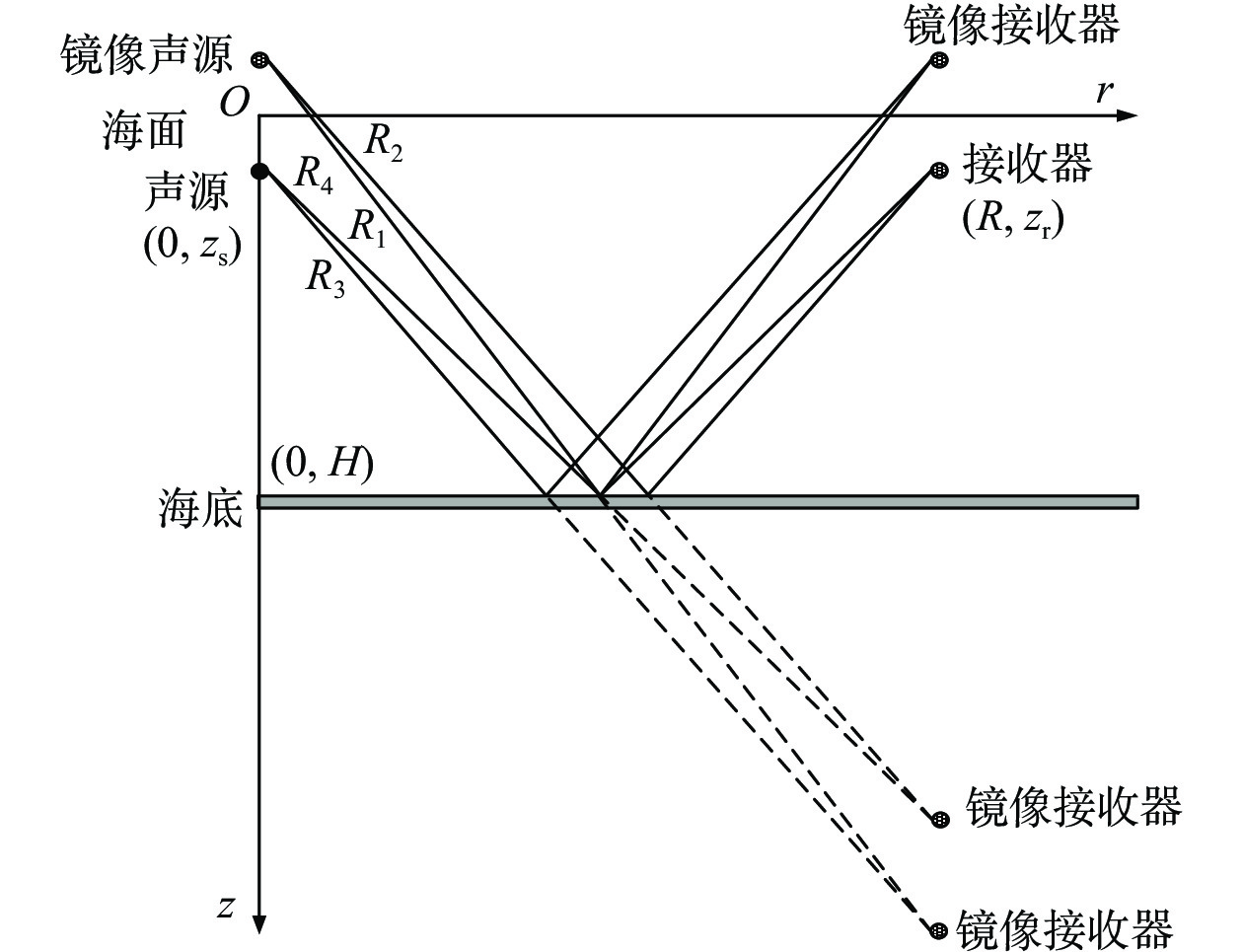
这里把经海面和海底反射的声线看成是由各自虚源发出的声线,可以将海底声反射区声场用虚源模型进行表示。建立如图10所示的坐标系 $rO\textit{z}$ , 假设深海海深为 $H$ , 水中声速取等效的常数值(值为 $c$ ), 声源距海面垂直深度为 ${\textit{z}_{\rm s}}$ , 接收器距海面垂直深度为 ${\textit{z}_{\rm r}}$ , 收发水平距离为 $R$ , 声源与镜像声源到接收器与镜像接收器之间的斜距分别为 ${R_1},{\text{ }}{R_2},{\text{ }}{R_3},{\text{ }}{R_4}$ 。从图中根据几何关系可以推导出4条声线路径的斜距分别为

图 10 基于虚源理论的海底声反射区示意图

下载: 全尺寸图片幻灯片

$\begin{split}& {R_1} = \sqrt {{R^2} + {{\left( {2H - {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}} \right)}^2}} {\text{, }}{R_2} = \sqrt {{R^2} + {{\left( {2H + {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}} \right)}^2}} , \\& {R_3} = \sqrt {{R^2} + {{\left( {2H - {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}} \right)}^2}} {\text{, }}{R_4} = \sqrt {{R^2} + {{\left( {2H + {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}} \right)}^2}} . \end{split}$

(6)

经过一次海底反射的接收信号是图中4条声线到达信号的叠加。声源发射角频率为 $\omega$ 的信号, 不考虑海洋环境各向异性声散射给声场带来的背景干扰影响, 略去时间因子, 当声源和接收器都接近海面时, 接收点的叠加声场可以近似表示为

$\begin{split} P\left( {{\textit{z}_{\rm s}},{\textit{z}_{\rm r}},r;\omega } \right) =& S\left( \omega \right)\left[ {V_{\rm b}}\frac{{{{\text{e}}^{{\text{i}}\omega {R_1}/c}}}}{{{R_1}}} + {V_{\rm s}}{V_{\rm b}}\frac{{{{\text{e}}^{{\text{i}}\omega {R_2}/c}}}}{{{R_2}}} +\right.\\&\left. {V_{\rm b}}{V_{\rm s}}\frac{{{{\text{e}}^{{\text{i}}\omega {R_3}/c}}}}{{{R_3}}} + {V_{\rm s}}{V_{\rm b}}{V_{\rm s}}\frac{{{{\text{e}}^{{\text{i}}\omega {R_4}/c}}}}{{{R_4}}} \right], \end{split}$

(7)

其中, $S$ 为声源强度, ${V_{\rm b}}$ 为海底声压反射系数, ${V_{\rm s}}$ 为海面声压反射系数, 默认海面近似为自由界面, 则 ${V_{\rm s}} = - 1$ 。根据声线时延差的定义可以将 ${\tau _{{\text{SBSR-BR}}}}$ , ${\tau _{{\text{BSR-BR}}}}$ , ${\tau _{{\text{SBSR-SBR}}}}$ , ${\tau _{{\text{BSR-SBR}}}}$ , ${\tau _{{\text{SBR-BR}}}}$ , ${\tau _{{\text{SBSR-BSR}}}}$ 表示为如下表达式

$\begin{split}& {\tau _{{\text{SBSR-BR}}}} = \frac{{\sqrt {{R^2} + {{\left( {2H + {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}} \right)}^2}} - \sqrt {{R^2} + {{\left( {2H - {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}} \right)}^2}} }}{c}, \\& {\tau _{{\text{BSR-BR}}}} = \frac{{\sqrt {{R^2} + {{\left( {2H - {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}} \right)}^2}} - \sqrt {{R^2} + {{\left( {2H - {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}} \right)}^2}} }}{c}, \\& {\tau _{{\text{SBSR-SBR}}}} = \frac{{\sqrt {{R^2} + {{\left( {2H + {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}} \right)}^2}} - \sqrt {{R^2} + {{\left( {2H + {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}} \right)}^2}} }}{c}, \\& {\tau _{{\text{BSR-SBR}}}} = \frac{{\sqrt {{R^2} + {{\left( {2H - {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}} \right)}^2}} - \sqrt {{R^2} + {{\left( {2H + {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}} \right)}^2}} }}{c}, \\& {\tau _{{\text{SBR-BR}}}} = \frac{{\sqrt {{R^2} + {{\left( {2H + {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}} \right)}^2}} - \sqrt {{R^2} + {{\left( {2H - {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}} \right)}^2}} }}{c}, \\& {\tau _{{\text{SBSR-BSR}}}} = \frac{{\sqrt {{R^2} + {{\left( {2H + {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}} \right)}^2}} - \sqrt {{R^2} + {{\left( {2H - {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}} \right)}^2}} }}{c}. \end{split}$

(8)

以 ${\tau _{{\text{SBSR-BR}}}}$ 为例, 说明化简过程。由于在深海海底声反射区环境下, $\left( {2H + {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}} \right)/R < < 1$ , 因此可以通过小量近似 ${\left( {1 + a} \right)^{1/2}} \approx 1 + a/2$ 来化简 ${\tau _{{\text{SBSR-BR}}}}$ 表达式, 具体过程如下:

$\begin{split}& {\tau _{{\text{SBSR-BR}}}} = \frac{{\sqrt {{R^2} + {{\left( {2H + {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}} \right)}^2}} - \sqrt {{R^2} + {{\left( {2H - {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}} \right)}^2}} }}{c} = \\& \frac{1}{c}\left( {\sqrt {{R^2}\left( {1 + {{\left( {\frac{{2H + {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}}}{R}} \right)}^2}} \right)} - \sqrt {{R^2}\left( {1 + {{\left( {\frac{{2H - {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}}}{R}} \right)}^2}} \right)} } \right) = \\& {\text{ }} \frac{R}{c}\left( {{{\left( {1 + {{\left( {\frac{{2H + {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}}}{R}} \right)}^2}} \right)}^{\frac{1}{2}}} - {{\left( {1 + {{\left( {\frac{{2H - {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}}}{R}} \right)}^2}} \right)}^{\frac{1}{2}}}} \right)\approx \\& {\text{ }} \frac{R}{c}\left( {1 + \frac{1}{2}{{\left( {\frac{{2H + {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}}}{R}} \right)}^2} - 1 - \frac{1}{2}{{\left( {\frac{{2H - {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}}}{R}} \right)}^2}} \right)= \\& \frac{1}{{2cR}}\left( {{{\left( {2H + {\textit{z}_{\rm s}} + {\textit{z}_{\rm r}}} \right)}^2} - {{\left( {2H - {\textit{z}_{\rm s}} - {\textit{z}_{\rm r}}} \right)}^2}} \right) = {\text{ }}\frac{{4H}}{{cR}}{\textit{z}_{\rm r}} + \frac{{4H{\textit{z}_{\rm s}}}}{{cR}}. \end{split}$

(9)

同理可化简其他时延差表达式, 分别为

$\begin{split}& {\tau _{{\text{SBSR-BR}}}} \approx \frac{{4H}}{{cR}}{\textit{z}_{\rm r}} + \frac{{4H{\textit{z}_{\rm s}}}}{{cR}}, \;\; {\tau _{{\text{BSR-BR}}}} \approx \frac{{4H - 2{\textit{z}_{\rm s}}}}{{cR}}{\textit{z}_{\rm r}}, \\& {\tau _{{\text{SBSR-SBR}}}} \approx \frac{{4H + 2{\textit{z}_{\rm s}}}}{{cR}}{\textit{z}_{\rm r}},\;\; {\tau _{{\text{BSR-SBR}}}} \approx \frac{{4H}}{{cR}}{\textit{z}_{\rm r}} - \frac{{4H{\textit{z}_{\rm s}}}}{{cR}}, \\& {\tau _{{\text{SBR-BR}}}} \approx - \frac{{2{\textit{z}_{\rm s}}}}{{cR}}{\textit{z}_{\rm r}} + \frac{{4H{\textit{z}_{\rm s}}}}{{cR}}, \;\; {\tau _{{\text{SBSR-BSR}}}} \approx \frac{{2{\textit{z}_{\rm s}}}}{{cR}}{\textit{z}_{\rm r}} + \frac{{4H{\textit{z}_{\rm s}}}}{{cR}}. \end{split}$

(10)

根据上述表达式可以总结出以下特征:

(1) 由于 $2{\textit{z}_{\rm s}} < < cR$ , ${\textit{z}_{\rm s}}/(cR) \approx 0$ , 因此4条曲线的斜率 ${k_{{\text{SBSR-BR}}}} \approx {k_{{\text{BSR-BR}}}} \approx {k_{{\text{SBSR-SBR}}}} \approx {k_{{\text{BSR-SBR}}}} \approx 4H/(cR)$ ;

(2) 由于 $2{\textit{z}_{\rm s}} < < cR$ , $2{\textit{z}_{\rm s}}/(cR) \approx 0$ , 因此2条曲线的斜率 ${k_{{\text{SBR-BR}}}} \approx {k_{{\text{SBSR-BSR}}}} \approx 0$ ;

(3) 当 ${\textit{z}_{\rm r}} = {\textit{z}_{\rm s}}$ 时, ${\tau _{{\text{BSR-SBR}}}} = 0$ , 由于 ${\textit{z}_{\rm s}}^2 < < cR$ , 因此时延差 ${\tau _{{\text{BSR-BR}}}} \approx {\tau _{{\text{SBSR-SBR}}}} \approx {\tau _{{\text{SBR-BR}}}} \approx {\tau _{{\text{SBSR-BSR}}}} \approx 4H{\textit{z}_{\rm s}}/(cR)$ ;

(4) 当 ${\textit{z}_{\rm r}} = 2{\textit{z}_{\rm s}}$ 时, 由于 $4{\textit{z}_{\rm s}}^2 < < cR$ , 因此时延差 ${\tau _{{\text{SBR-BSR}}}} \approx {\tau _{{\text{SBR-BR}}}} \approx {\tau _{{\text{SBSR-BSR}}}} \approx 4H{\textit{z}_{\rm s}}/(cR)$ ;

(5) 当 ${\textit{z}_{\rm r}} = 0$ 时, 初始时延差值 $\left| {{\tau _{{\text{BSR-SBR}}}}} \right| \approx \left| {{\tau _{{\text{SBR-BR}}}}} \right| \approx \left| {{\tau _{{\text{SBSR-BSR}}}}} \right| \approx 4H{\textit{z}_{\rm s}}/(cR)$ 。

为验证上述特征的正确性, 将图9中的仿真条件 $H = 4314.5{\text{ m}}$ , $R = 18{\text{ km}}$ , $c = 1525{\text{ m/s}}$ , ${\textit{z}_s} = 200{\text{ m}}$ 代入式(10), 可得:

(1) ${k_{{\text{SBSR-BR}}}} \approx {k_{{\text{BSR-BR}}}} \approx {k_{{\text{SBSR-SBR}}}} \approx {k_{{\text{BSR-SBR}}}} \approx 0.6287$ , 利用线性拟合函数对图9中 ${k_{{\text{SBSR-BR}}}}$ , ${k_{{\text{BSR-BR}}}}$ , ${k_{{\text{SBSR-SBR}}}}$ , ${k_{{\text{BSR-SBR}}}}$ 4条斜率进行拟合, 拟合的平均斜率 ${k_1} \approx 0.6308$ , 平均残差范数为20.83;

(2) ${k_{{\text{SBR-BR}}}} \approx {k_{{\text{SBSR-BSR}}}} \approx 0.0145$ , 利用线性拟合函数对图9中 ${k_{{\text{SBR-BR}}}}$ 和 ${k_{{\text{SBSR-BSR}}}}$ 2条斜率进行拟合, 拟合的平均斜率 ${k_2} \approx 0.0125$ , 平均残差范数为2.51;

(3) 当 ${\tau _{{\text{BSR-SBR}}}} = 0$ 时, 图9中横坐标对应的深度 ${\textit{z}_{\rm r1}} = 200{\text{ m}} = {\textit{z}_{\rm s}}$ ;

(4) 当 ${\tau _{{\text{BSR-BR}}}}$ , ${\tau _{{\text{SBSR-SBR}}}}$ , ${\tau _{{\text{SBR-BR}}}}$ , ${\tau _{{\text{SBSR-BSR}}}}$ 4条曲线两两相交时, 图9中交点处对应横坐标的平均值 ${\textit{z}_{\rm r2}} = 200.6{\text{ m}} \approx {\textit{z}_{\rm s}}$ ;

(5) 当 ${\tau _{{\text{SBR-BSR}}}}$ , ${\tau _{{\text{SBR-BR}}}}$ , ${\tau _{{\text{SBSR-BSR}}}}$ 3条曲线两两相交时, 图9中交点处对应横坐标的平均值 ${\textit{z}_{\rm r3}} = 401~ {\rm m} \approx 2{\textit{z}_{\rm s}}$ ;

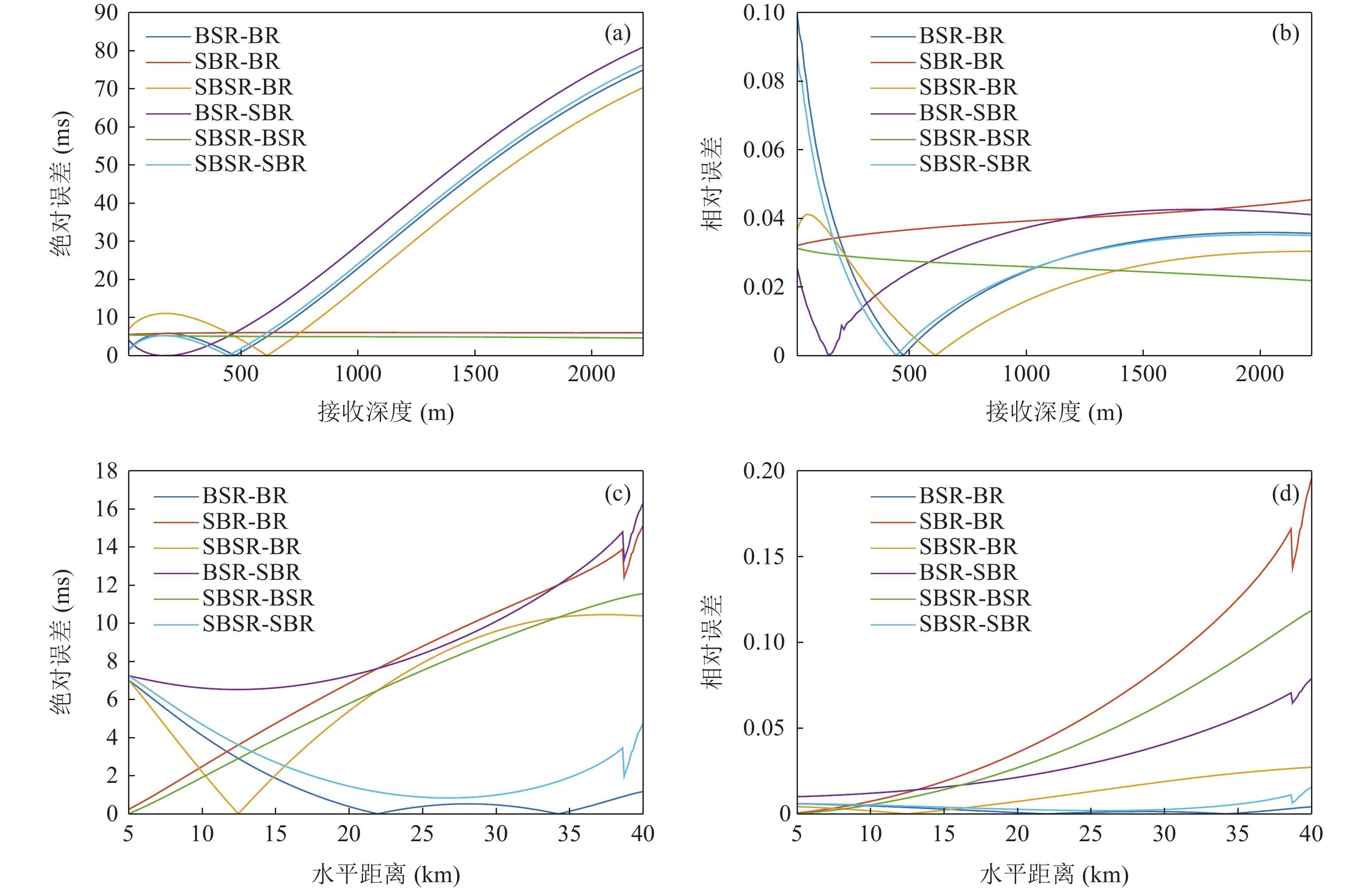
(6) 当 ${\textit{z}_{\rm r}} = 0$ 时, $\left| {{\tau _{{\text{BSR-SBR}}}}} \right| \approx \left| {{\tau _{{\text{SBR-BR}}}}} \right| \approx \left| {{\tau _{{\text{SBSR-BSR}}}}} \right| \approx 125.74{\text{ ms}}$ , 图9中初始深度 ${\textit{z}_{\rm r0}} = 20{\text{ m}}$ 时3条曲线的平均时延差 ${\tau _0} = 121.96{\text{ ms}}$ 。

以上6项信息均符合表达式推导得到的特征, 证明了利用四元虚源理论推导海底声反射区4条声线到达路径时延差表达式的正确性。图11分别给出了水平距离为18 km时利用虚源模型计算的4条声线到达路径时延差与射线模型计算的4条声线到达路径时延差之间随接收深度变化的绝对误差值和相对误差值以及接收深度在500 m时利用虚源模型计算的4条声线到达路径时延差与射线模型计算的4条声线到达路径时延差之间随水平距离变化的绝对误差值和相对误差值。从图中可以看出, 随着接收深度和水平距离的增大, 虚源模型与射线模型计算的时延差之间的相对误差值逐渐增大, 但始终保持在0.2以内。因此, 利用虚源模型推导的时延差表达式, 结合图9中拟合的6条曲线斜率可以估计声源的水平距离, 距离估计值 $R = 4H/(c{k_1}) \approx 17.94{\text{ km}}$ , 距离估计误差为0.33%; 利用图9中 ${\tau _{{\text{BSR-SBR}}}} = 0$ 和两个相交点集的平均横坐标可以估计声源的深度, 深度估计值 ${\textit{z}_{\rm s}} = \left( {{\textit{z}_{\rm r1}} + {\textit{z}_{\rm r2}} + {\textit{z}_{\rm r3}}} \right)/4 \approx 200.25{\text{ m}}$ , 深度估计误差为0.13%。

图 11 虚源模型与射线模型计算的时延差误差值随水平距离和深度的变化结果 (a) 水平距离为18 km时的绝对误差; (b) 水平距离为18 km时的相对误差; (c) 接收深度为500 m时的绝对误差; (d) 接收深度为500 m时的相对误差

下载: 全尺寸图片幻灯片

3. 基于Radon变换的改进定位方法

当接收信噪比较低、利用接收信号难以准确提取出4条声线路径的到达时间结构时, 可以运用自相关的方法直接求出时延差, 得到的时延差值随接收深度的变化如图12所示，仿真条件同第1节。图中曲线的变化规律与图9一致, 引入Radon技术对该图像进行处理。

图 12 时延差值随接收深度的变化结果

下载: 全尺寸图片幻灯片

Radon图像处理技术是Johann Radon提出的一种曲线参数估计方法, 本文只考虑直线情况。假定图像中的直线表达式为: $y = kx + b$ , $k$ 为直线的斜率, $b$ 为直线的截距, $x$ 和 $y$ 为变量, 利用Radon变换进行积分, 可以将原图像转换为以 $\rho$ 和 $\theta$ 为变量的参数空间, 其中 $\rho$ 为图像空间在参数空间中投影的长度, 表示原点到直线的垂直距离, 有正负号; $\theta$ 为参数空间相对于图像空间旋转的角度, 表示直线法线方向的夹角, 直线与x轴平行为90°, 垂直为0°或180°。Radon变换技术对图像空间中的各点 $\left( {x,y} \right)$ 进行逐个积分, 将满足要求的直线上的点全部积分累加到参数空间的点 $\left( {\rho ,\theta } \right)$ 上, 根据记录累积量的相对大小来确定 $\left( {x,y} \right)$ 空间上直线的存在性。设 $f\left( {x,y} \right)$ 为定义在 $\left( {x,y} \right)$ 平面 $D$ 上的普通任意连续函数, 则 $f$ 的Radon变换表达式如下:

$R\left( {\rho ,\theta } \right) = \iint_D {f\left( {x,y} \right)\delta \left( {\rho - x\cos \theta - y\sin \theta } \right){\text{d}}x{\text{d}}y},$

(11)

其中, $\delta$ 为狄拉克函数,

$\delta \left( t \right) = \left\{ {\begin{array}{*{20}{c}} {1,}&{t = 0,} \\ {0,}&{t \ne 0.} \end{array}} \right.$

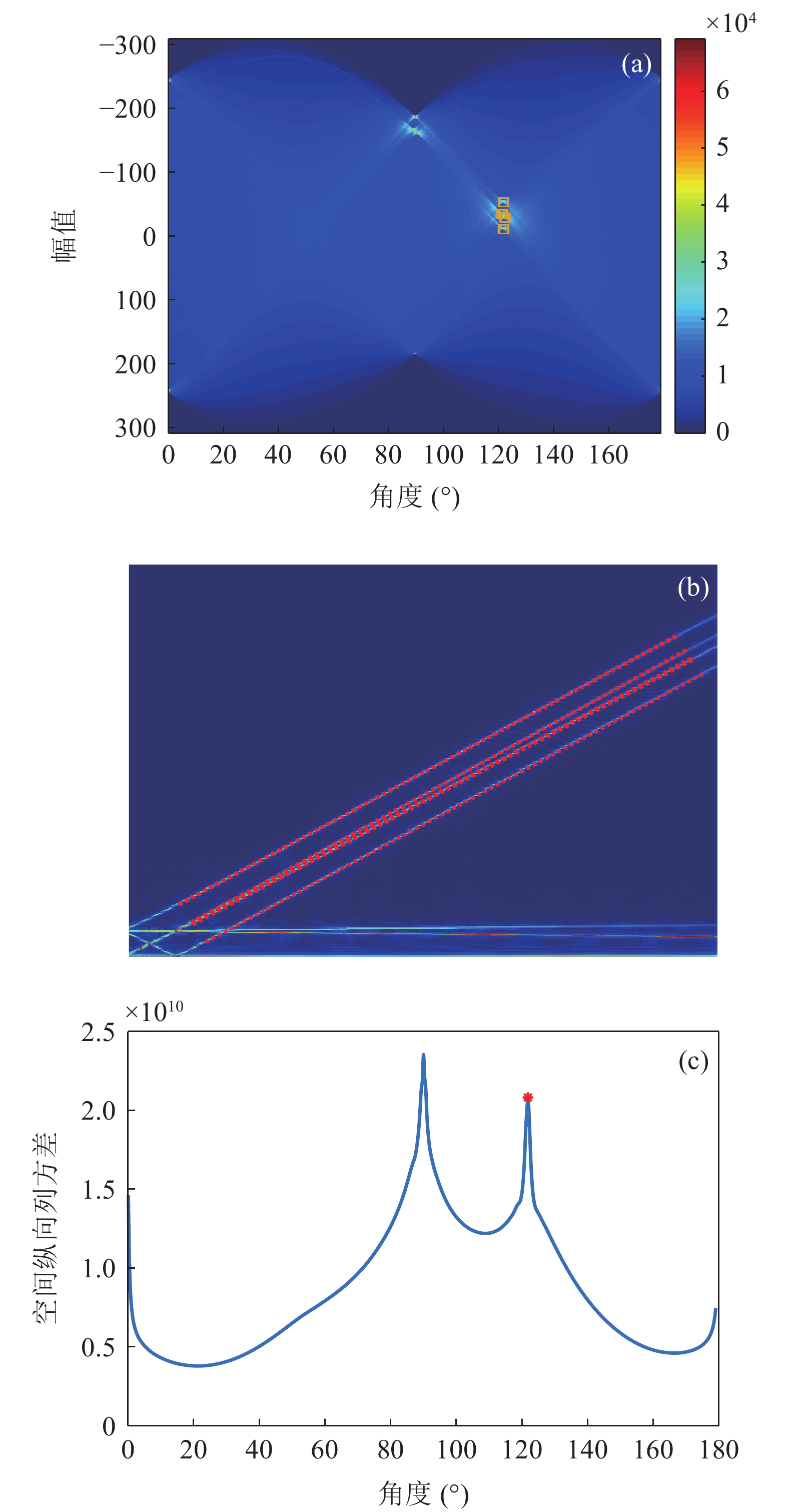
以图12为例, 进行Radon变换后得到的变换结果如图13(a)所示。图中横坐标角度接近90°的极值点为 ${\tau _{{\text{SBR-BR}}}}$ 和 ${\tau _{{\text{SBSR-BSR}}}}$ 曲线, 斜率近似为0。图13(b)给出了通过Radon变换恢复的4条曲线, 可以看出, 4条曲线的斜率角 $\theta$ 近似相等, 投影长度 $\rho$ 不等。由于本文只需要获得直线的斜率, 因此对Radon空间沿 $\rho$ 方向求方差以获得更高的估计精度和更好的稳健性。考虑到实际情况下 $R\left( {\rho ,\theta } \right)$ 分布离散, 因此利用

图 13 Radon变换仿真结果 (a) 参数空间; (b) 恢复图像; (c) 纵向列方差

下载: 全尺寸图片幻灯片

$D\left( \theta \right) = {\sum\limits_\rho {\left( {R\left( {\rho ,\theta } \right) - \overline {R\left( {\rho ,\theta } \right)} } \right)} ^2}{\text{ }}$

(12)

计算Radon变换矩阵在 $\theta$ 处的列方差值 $D\left( \theta \right)$ , 得到的空间纵向列方差结果如图13(c)所示。

通过图13(c)可以得到, 4条声线路径的时延差曲线与x轴的夹角为31.9°, 斜率值为0.6224, 代入表达式 $R \approx 4H/(ck)$ 可得声源的水平估计距离为18.18 km, 估计误差为1%。

接下来对声源深度进行估计。上文提到的“零点”和“交点”估计法在声源深度附近接收阵元较密集或信噪比较高的情况下是较为简单直观的, 可以不经过计算, 直接通过图像估计出大致的声源深度值。然而在实际操作中, 接收阵元的布置往往是稀疏且随机的, 尤其当信噪比较低的时候, 很难再通过“零点”和“交点”直接估计出声源深度。此时需要利用声源已估计出的水平距离结果, 结合 ${\tau _{{\text{SBR-BR}}}}$ 和 ${\tau _{{\text{SBSR-BSR}}}}$ 曲线的初始时延差值对声源深度进行间接估计。已知接收深度为0时, ${\tau _{{\text{SBR-BR}}}} = {\tau _{{\text{SBSR-BSR}}}} = 4H{\textit{z}_{\rm s}}/(cR)$ 。由于 ${\textit{z}_{\rm s}}/(cR) < < 1$ , 且 $\left| {{k_{{\text{SBR-BR}}}}} \right| = \left| {{k_{{\text{SBSR-BSR}}}}} \right| < < 1$ , 因此 ${\textit{z}_r}$ 在一定取值范围内都可以认为 ${\textit{z}_{\rm s}}{\textit{z}_{\rm r}}/(cR)$ 趋近于0, 因此初始时延差值 ${\tau _{{\text{SBR-BR}}}} \approx {\tau _{{\text{SBSR-BSR}}}} \approx 4H{\textit{z}_{\rm s}}/(cR)$ 。根据图12可以得到, 接收阵元在最浅深度20 m时， ${\tau _{{\text{SBR-BR}}}} = {\tau _{{\text{SBSR-BSR}}}} = 1{\text{21}}{\text{.96 ms}}$ , 结合前面估计出的声源水平距离18.18 km, 代入表达式 ${\textit{z}_{\rm s}} \approx cR{\tau _{{\text{SBR-BR}}}}/(4H) \approx cR{\tau _{{\text{SBSR-BSR}}}}/ (4H)$ 可得声源深度的估计值 ${\textit{z}_{\rm s}} \approx 195.93{\text{ m}}$ , 深度估计误差为2%。

4. 影响因素分析

影响本文所提方法的主要因素有信噪比、声速和阵列孔径, 下面通过对这3个参数进行仿真分析来研究本文所提方法的适用性能。

4.1 接收信噪比

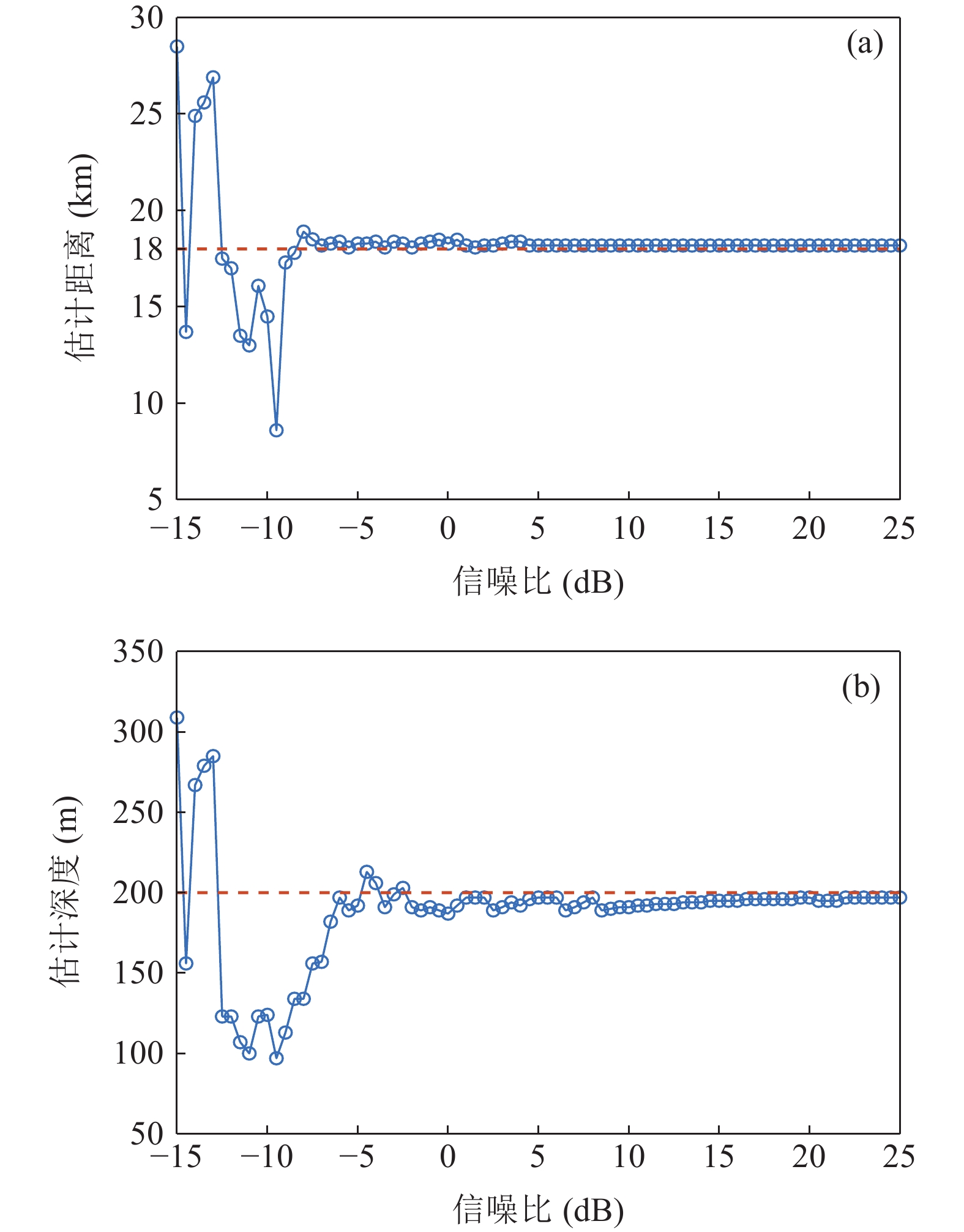
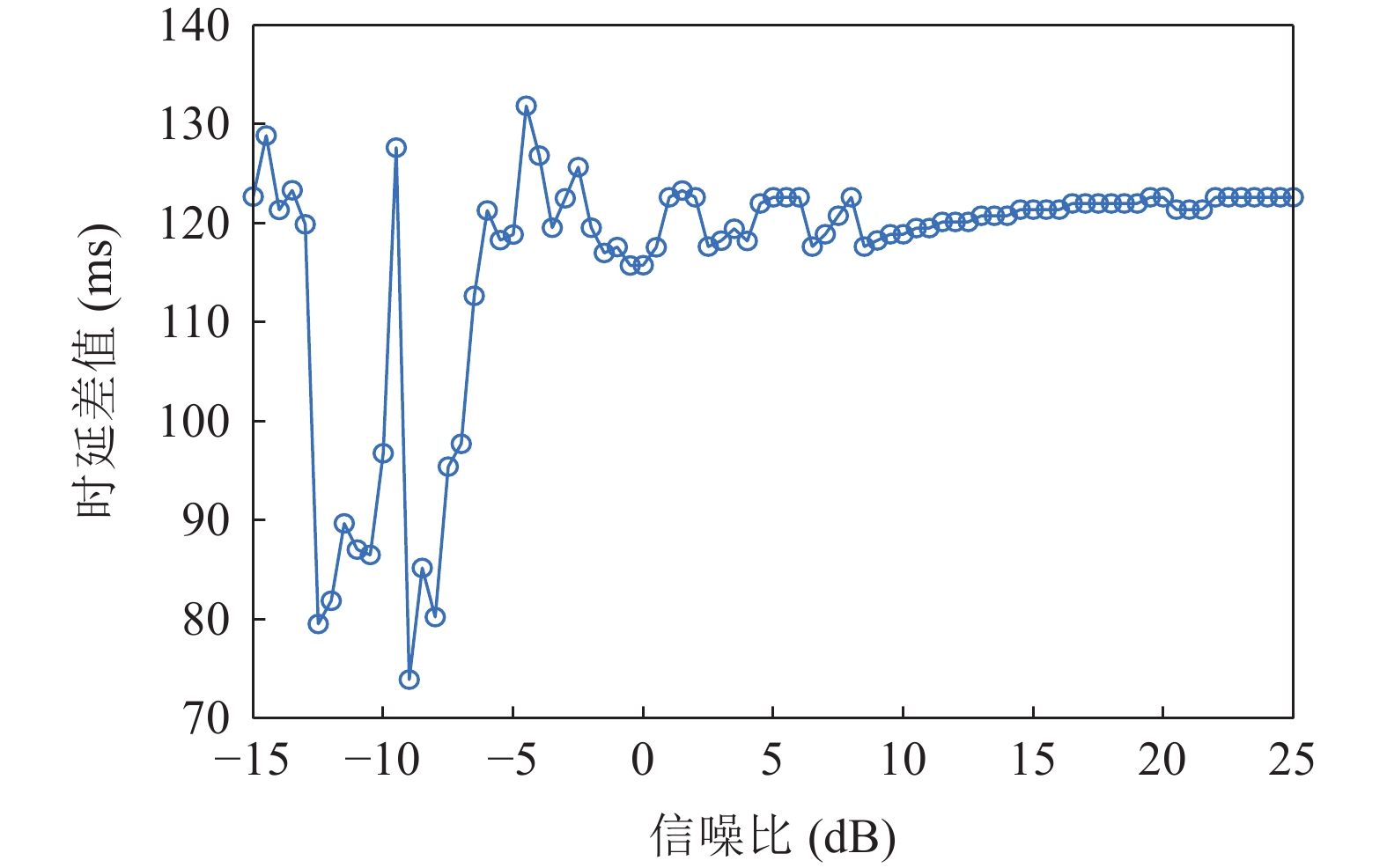
为了研究平均接收阵元信噪比变化对声源距离和深度估计性能的影响, 仿真研究了收发距离为18 km、深度为200 m的声源在不同信噪比条件下的距离估计结果和深度估计结果, 如图14所示。仿真条件同第1节。可以看出, 当接收信噪比低于−9 dB时, 难以估计出有效的声源距离信息; 当接收信噪比高于−9 dB时，声源距离估计结果逐渐接近真实值; 当接收信噪比高于5 dB时, 声源距离估计结果趋于稳定。当接收信噪比低于−7 dB时, 深度估计结果有明显的振荡现象, 声源深度估计结果错误; 当接收信噪比高于−7 dB时，声源深度估计结果逐渐接近真实深度; 当接收信噪比高于8 dB时, 声源深度估计结果趋于稳定。对比图14(a)和图14(b)可以看出, 声源有效估计深度的临界信噪比高于有效估计距离的临界信噪比, 这是因为在声源深度估计时, 除了运用到距离估计信息以外, 还需要提取初始接收深度的时延差值, 时延差值随接收信噪比的变化如图15所示。从图中可以看出, 当接收信噪比高于8 dB时, 初始接收深度的时延差值结果趋于稳定, 由此可以得出, 声源深度的估计误差受初始接收深度的时延差值误差影响要大于距离估计误差的影响。

图 14 声源估计结果随接收信噪比的变化关系 (a) 距离估计结果; (b) 深度估计结果

下载: 全尺寸图片幻灯片

图 15 初始时延差值随接收信噪比的变化关系

下载: 全尺寸图片幻灯片

4.2 等效声速

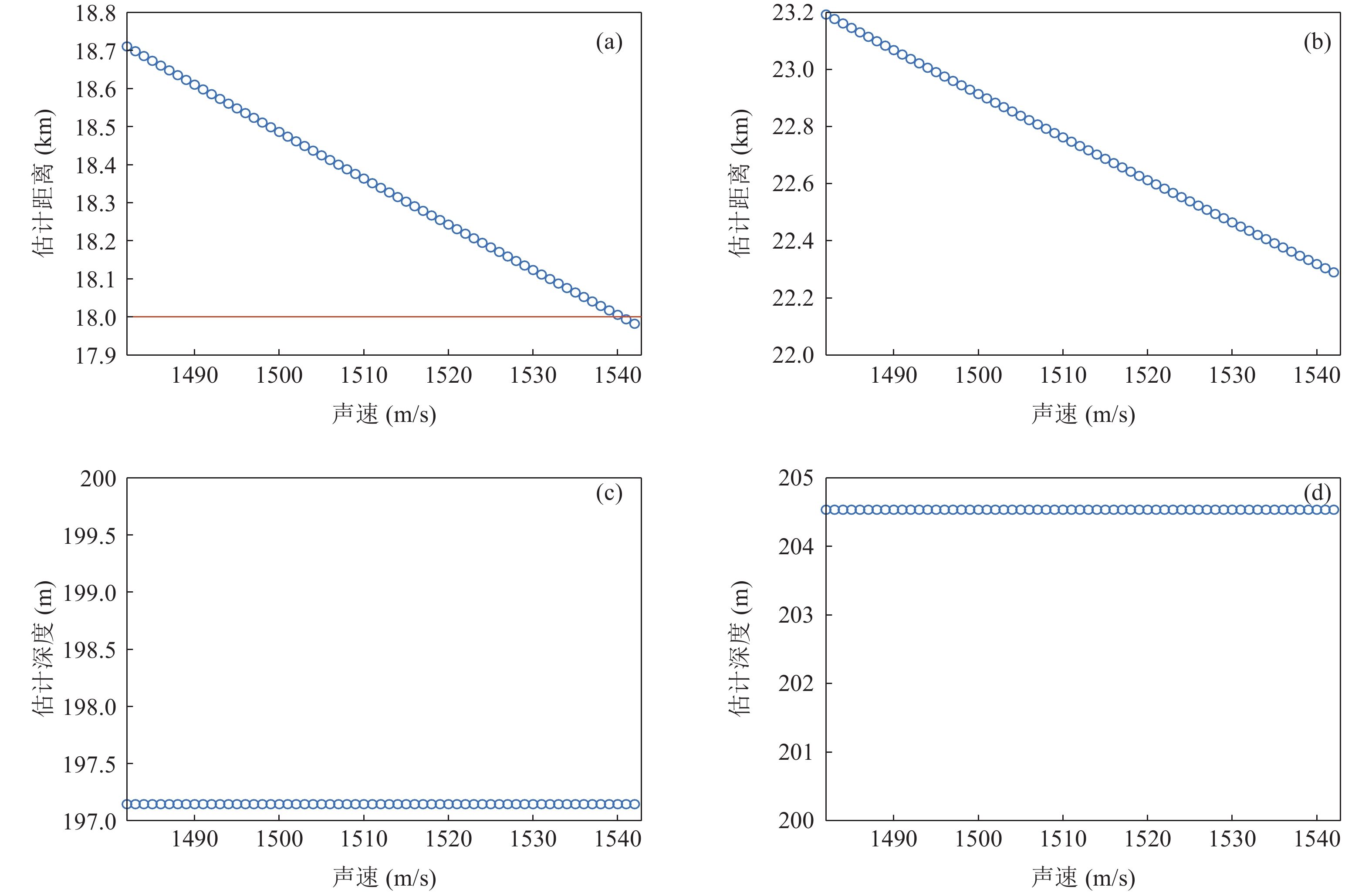
根据表达式 $R \approx 4H/(ck)$ 和 ${z_{\rm s}} \approx cR{\tau _{{\text{SBR-BR}}}}/(4H) \approx cR{\tau _{{\text{SBSR-BSR}}}}/ (4H)$ 可以看出, 声源的距离和深度估计均涉及到等效声速c, 等效声速c在计算过程中默认为一个常量, 但在实际情况下, 声速剖面通常随深度的变化而变化, 取不同深度的声速会得到不同的距离、深度估计结果。为了研究等效声速变化对声源距离和深度估计性能的影响, 在已知声速剖面的情况下, 改变声速取值, 开展声源距离和深度估计性能的仿真研究。

仿真研究收发距离为18 km和22 km、深度为200 m的声源, 在不同等效声速下的声源距离和深度估计结果，环境参数同第1节。声源信号频率范围为350~750 Hz, 声速范围由声速剖面决定, 取1482.0~1542.8 m/s，得到的声源距离和深度估计结果如图16所示。可以看出, 声源距离估计结果随声速取值的增大而减小, 声速取值对距离估计结果造成的整体影响较小。另外, 遍历垂直声速剖面声速值后可以发现, 声源距离估计结果始终接近真实值, 这是因为虚源理论建立在等声速环境的假设下, 没有考虑海水垂直声速梯度结构造成的影响。由图11可知，利用虚源模型和射线模型计算的时延差之间存在一定的误差, 因此导致声源距离估计结果也存在一定的理论误差。根据表达式

图 16 声源估计结果随等效声速的变化关系 (a) 水平距离为18 km时距离估计结果; (b) 水平距离为22 km时距离估计结果; (c) 水平距离为18 km时深度估计结果; (d) 水平距离为22 km时深度估计结果

下载: 全尺寸图片幻灯片

${\textit{z}_{\rm s}} \approx \frac{{cR{\tau _{{\text{SBR-BR}}}}}}{{4H}} \approx \frac{{cR{\tau _{{\text{SBSR-BSR}}}}}}{{4H}} \approx \frac{{{\tau _{{\text{SBR-BR}}}}}}{k} \approx \frac{{{\tau _{{\text{SBSR-BSR}}}}}}{k},$

声源深度估计结果只与初始接收深度的时延差值和计算得到的曲线斜率有关, 与等效声速没有直接关系, 又因为直线斜率与初始接收深度的时延差值受声速取值影响较小, 因此声源深度估计结果在声速取值变化时基本保持不变。

4.3 阵列孔径

阵列孔径表示的是阵列在空间占据的尺寸大小, 阵列孔径越大, 实际应用的工程实现越困难。相对阵列孔径指的是绝对阵列孔径与波长之比。一般情况下, 信噪比一定时, 适当增大阵列孔径和接收单元规模可以获得更多的空间增益。研究阵列孔径变化对声源距离和深度估计性能的影响, 可以在工程上利用最小的代价实现较好的声源距离和深度估计效果。

仿真研究收发距离为18 km、深度为200 m的声源, 在不同阵列长度下的声源距离和深度估计结果, 环境参数同第1节。声源频率为350~750 Hz, 第一个阵元的接收深度为20 m, 阵元间距为20 m, 阵列长度由200 m变化到1500 m。中心频率为550 Hz, 声速取1525 m/s, 则参考波长为2.77 m。取接收信噪比为−5 dB、5 dB和10 dB时的情况, 得到的声源距离和深度估计结果如图17所示。可以看出, 不同信噪比条件下所需要的基阵相对阵列孔径下限不同, 信噪比越高, 估计距离和深度所需要的相对阵列孔径越小。当信噪比大于5 dB时, 相对阵列孔径只需大于150即可获得有效的距离和深度估计结果; 而当信噪比小于−5 dB时, 相对阵列孔径则需要至少大于450才能获得可靠的距离和深度估计结果。本文所提方法对于相对阵列孔径的要求与信噪比一样, 来源于Radon变换中对时延差曲线斜率的提取和计算, 因此当相对阵列孔径过小或信噪比过低时, 会导致Radon变换计算直线斜率发生错误, 从而使得距离和深度的估计结果失效。

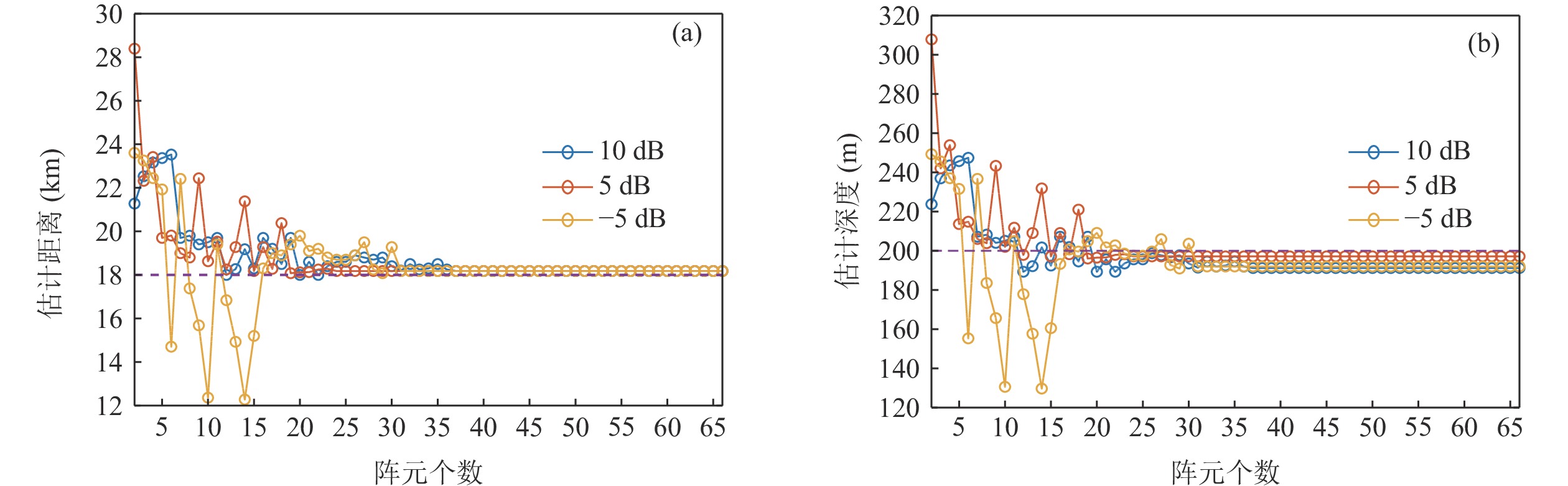
图 17 声源估计结果随相对阵列孔径的变化关系 (a) 距离估计结果; (b) 深度估计结果

下载: 全尺寸图片幻灯片

现研究阵元个数变化对声源距离和深度估计性能的影响。仿真研究收发距离为18 km、深度为200 m的声源, 在不同阵元个数下的声源距离和深度估计结果, 环境参数同第1节。声源频率为350~750 Hz, 第一个阵元的接收深度为20 m, 最后一个阵元的接收深度为2220 m, 阵元个数在2~70之间变化。取接收信噪比为−5 dB、5 dB和10 dB时的情况, 得到的声源距离和深度估计结果如图18所示。可以看出, 基阵相对阵列孔径一定时, 阵元个数下限几乎不随信噪比的变化而变化。当信噪比大于−5 dB时, 阵元个数只需大于32即可获得有效的距离和深度估计结果。对比图17和图18还可以发现, 本文所提方法对基阵相对阵列孔径的要求要高于对阵元个数的要求, 事实上研究信噪比与基阵相对阵列孔径和阵元个数下限的关系是有意义的, 可以明确针对不同信噪比目标所需要的基阵孔径和阵元个数, 减少布放成本。

图 18 声源估计结果随阵元个数的变化关系 (a) 距离估计结果; (b) 深度估计结果

下载: 全尺寸图片幻灯片

5. 实验数据验证

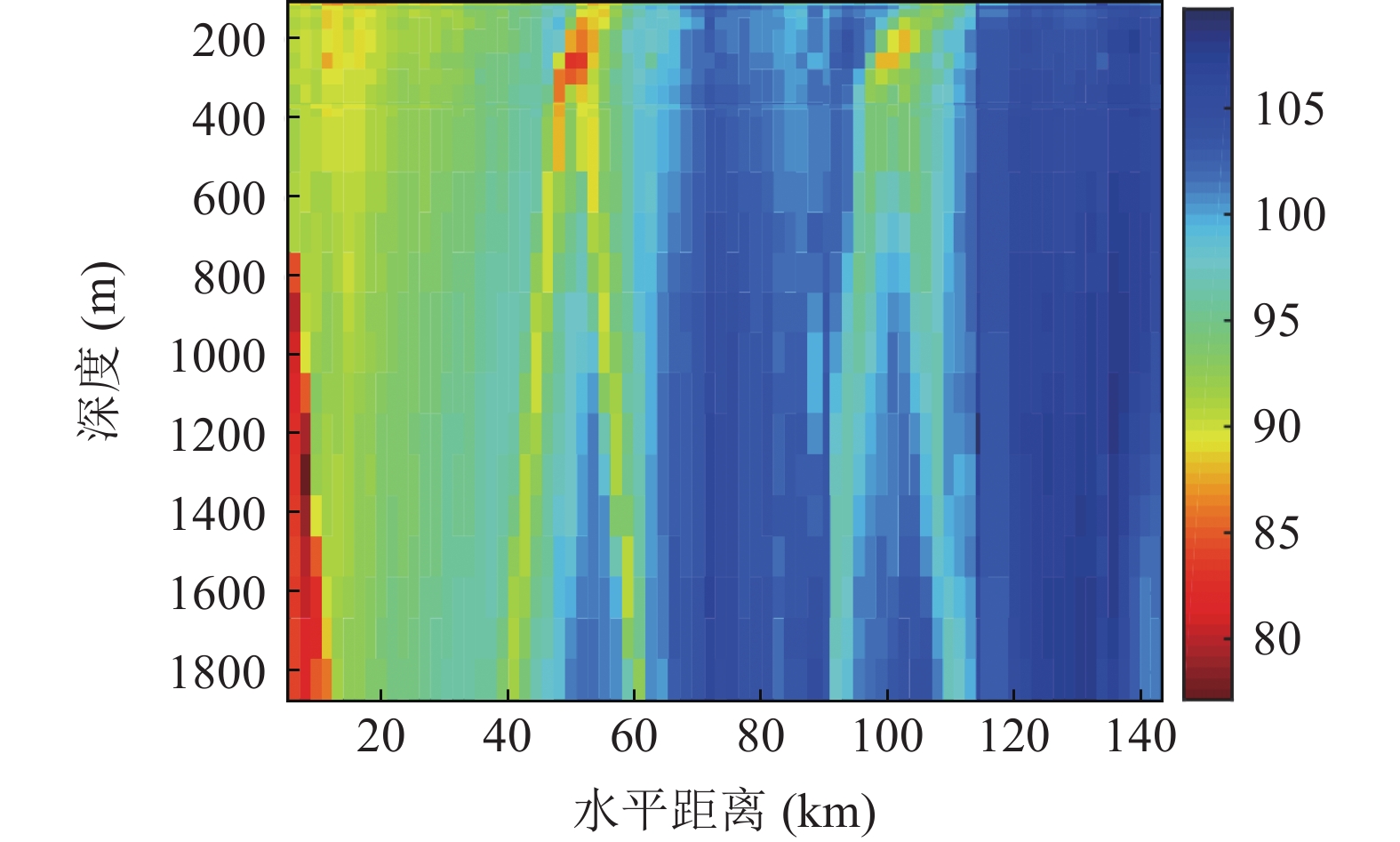
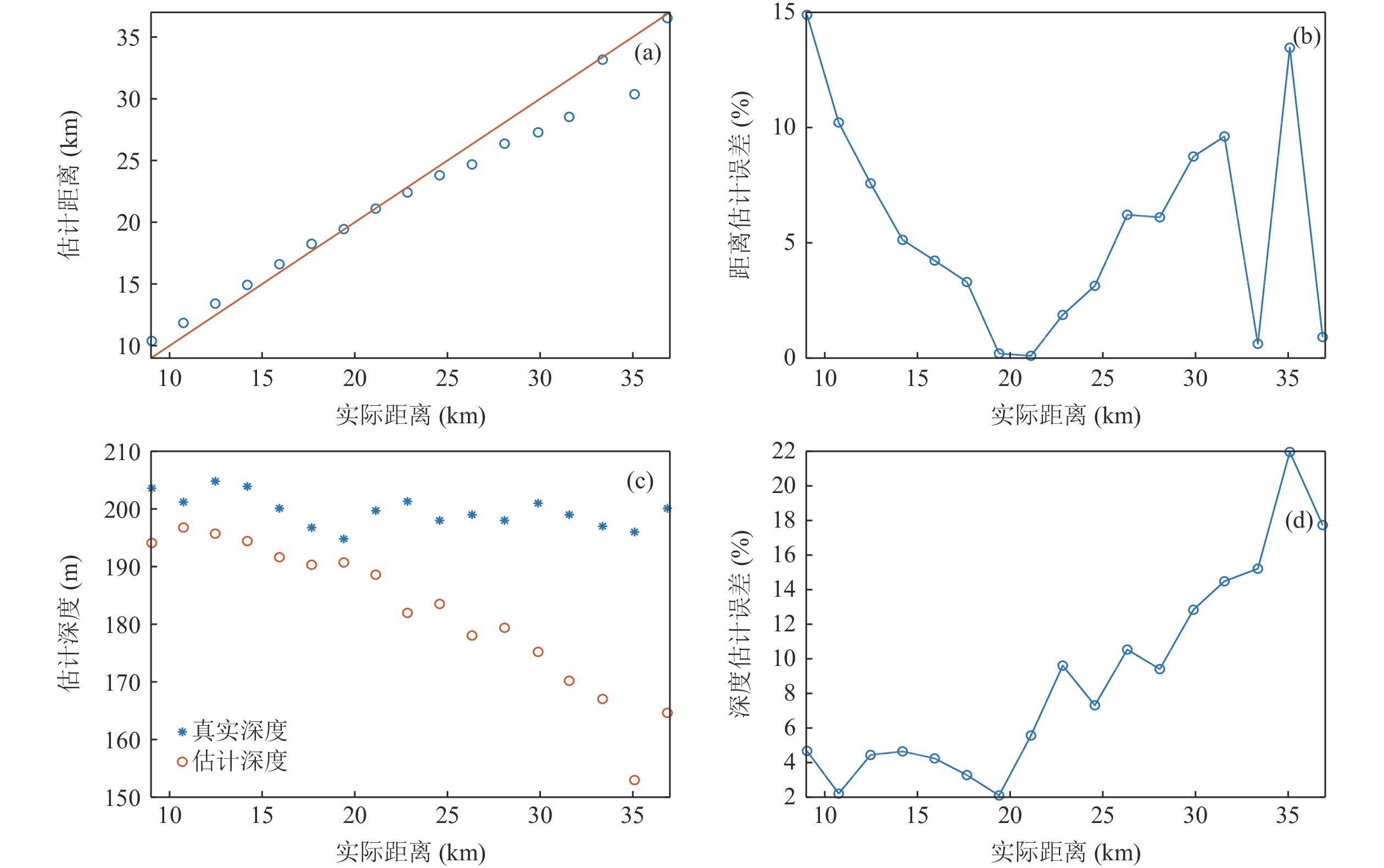
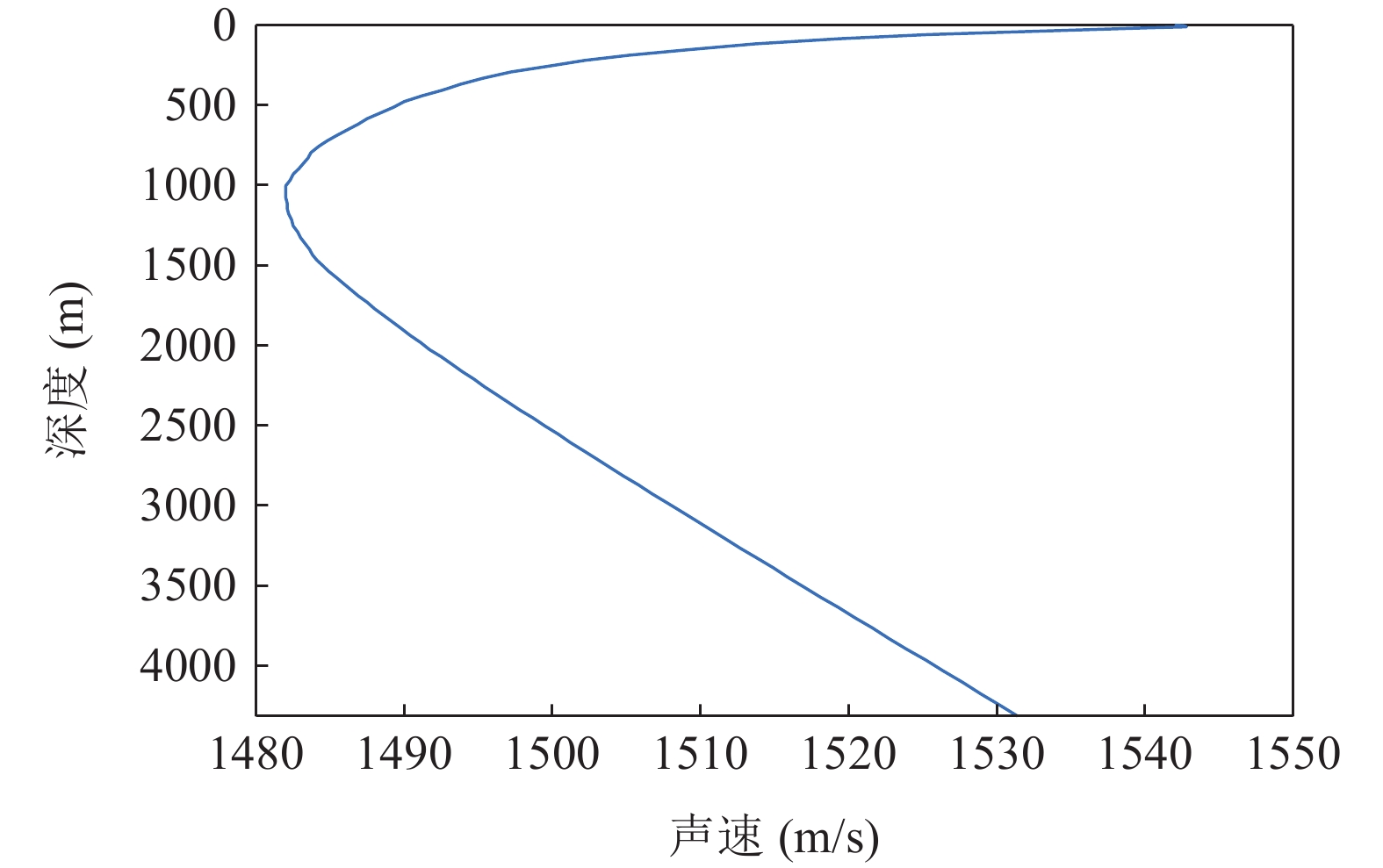
2014年6月在南海深海进行了一次深海声传播实验。接收阵为26阵元的自容式水听器阵, 非均匀地分布在111~1869 m的深度范围内, 采样率为16 kHz。实验船在传播测线上使用宽带爆炸声源作为发射信号, 爆炸声源标定深度为200 m, 当量为1000 g TNT。实验测线全程为350 km, 海底较为平坦, 平均海深约为4314.5 m。声传播实验期间测量的海水声速剖面如图19所示, 声道轴位于1000 m左右的深度上, 海底声速为1531 m/s, 海面处海水声速为1543 m/s。利用垂直阵得到的接收信号计算不同水平距离和深度处的传播损失, 得到的结果如图20所示。从图中可以看出, 本次实验中海底声反射区所在水平距离范围为9~37 km。

图 19 实验海区的垂直声速剖面

下载: 全尺寸图片幻灯片

图 20 实验测得的声传播损失图

下载: 全尺寸图片幻灯片

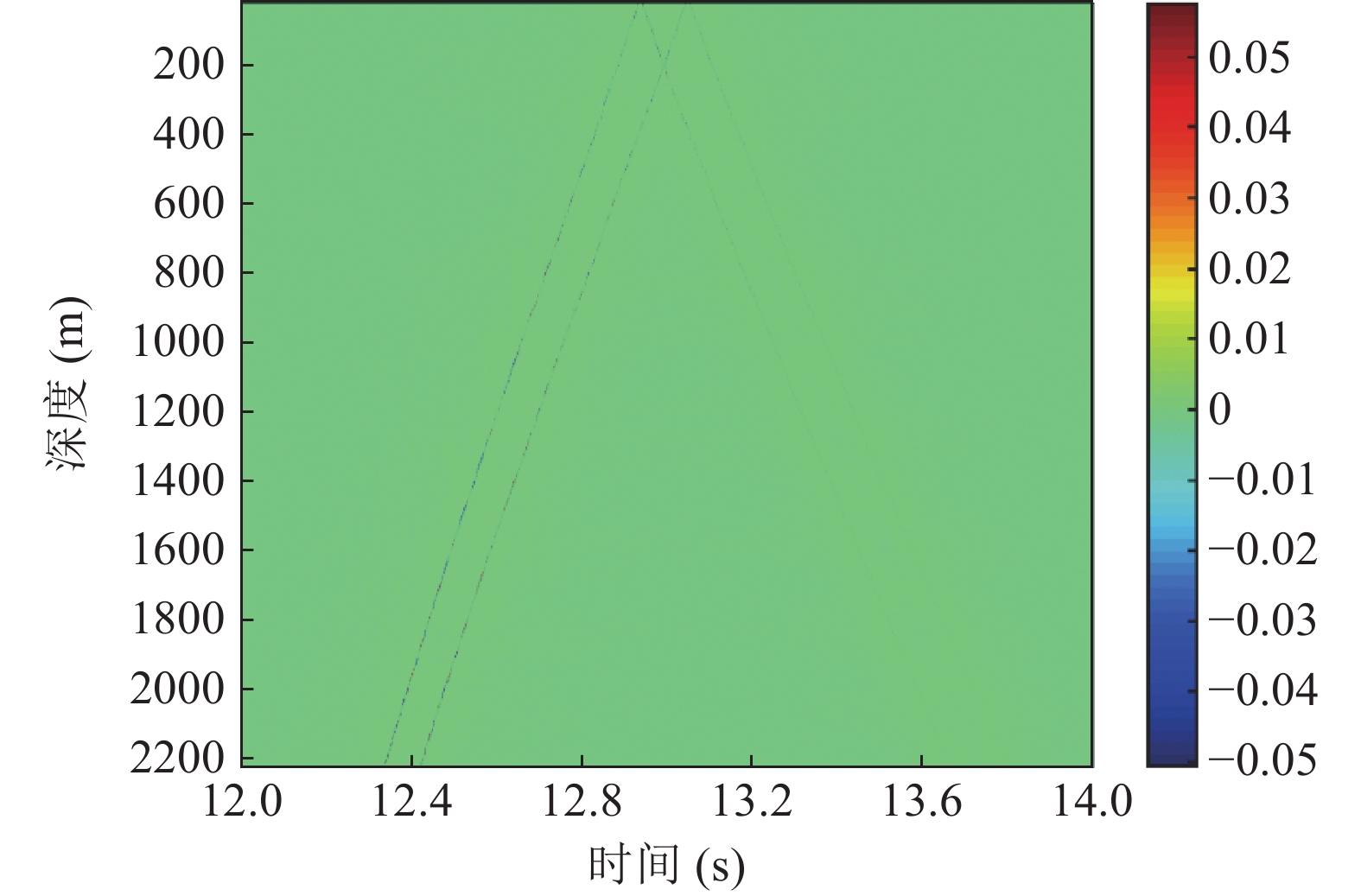
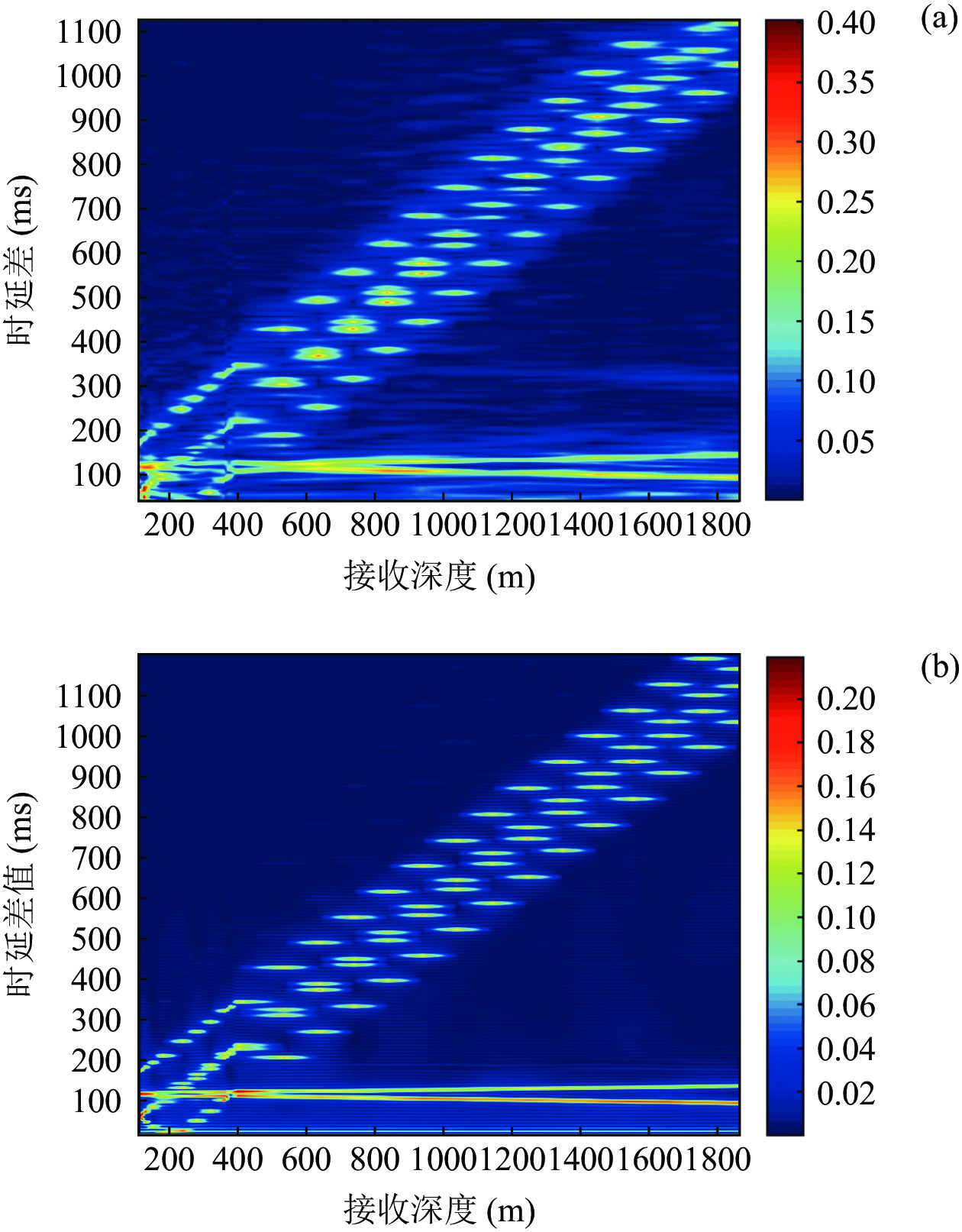
图21给出了实验中收发距离为17.67 km、接收深度为1869 m时的归一化接收信号包络图, 截取信号的频率范围为20~85 Hz。可以看出, 由于本次实验爆炸声源的信噪比较高, 因此利用接收信号的包络可以直接提取4条声线路径的时间簇峰值计算时延差, 时延差值随接收深度的变化曲线如图22所示。利用线性拟合函数对图22中的曲线斜率进行拟合, 拟合得到的平均斜率为0.6194, 取 $H = 4314.5{\text{ m}}$ , $c = 1525{\text{ m/s}}$ , 代入表达式 $R \approx 4H/(ck)$ 可得距离估计结果 $R \approx 18.27{\text{ km}}$ , 距离估计误差为3.4%。由于实验中接收阵元个数较少, 因此在提取相交点横坐标之前需要先对6条曲线进行线性插值, 提取插值后2个交点的横坐标平均值，分别为213.56 m和412.23 m (2倍声源深度), 平均声源深度估计结果 ${\textit{z}_{\rm r}} \approx 209.84{\text{ m}}$ , 深度估计误差为4.9％。

图 21 归一化接收信号包络

下载: 全尺寸图片幻灯片

图 22 时延差值随接收深度的变化结果

下载: 全尺寸图片幻灯片

为追求普遍性, 现模拟无法直接提取接收信号时间簇峰值的情况, 采用自相关方法对本次实验数据进行处理, 得到的时延差值随接收深度的变化如图23(a)所示，截取的信号频率范围为20~150 Hz。图23(b)给出了相同实验环境下Bellhop模型的计算结果。

图 23 时延差值随接收深度的变化结果 (a) 实验结果; (b) 模型计算结果

下载: 全尺寸图片幻灯片

对图23(a)进行Radon变换, 得到的变换结果如图24(a)所示。图中横坐标角度接近90°的极值点为 ${\tau _{{\text{SBR-BR}}}}$ 和 ${\tau _{{\text{SBSR-BSR}}}}$ 曲线, 斜率近似为0。图24(b)和图24(c)分别给出了通过Radon变换恢复的曲线和Radon空间纵向列方差结果。

图 24 Radon变换结果 (a) 参数空间; (b) 恢复图像; (c) 纵向列方差

下载: 全尺寸图片幻灯片

从图24(c)中可以得到, 4条声线路径的时延差曲线与x轴的平均夹角约为31.8°, 则斜率估计值为0.62, 代入表达式 $R \approx 4H/(ck)$ 可得水平估计距离为18.25 km, 估计误差为3.3%。根据图23可以得到, 接收阵元在最浅深度111 m处的时延差值 ${\tau _{{\text{SBR-BR}}}} = {\tau _{{\text{SBSR-BSR}}}} = 1{\text{15 ms}}$ , 将估计出的声源水平距离18.25 km代入表达式 ${\textit{z}_{\rm s}} \approx cR{\tau _{{\text{SBR-BR}}}}/(4H) \approx cR{\tau _{{\text{SBSR-BSR}}}}/ (4H)$ 可得声源深度估计值 ${\textit{z}_{\rm s}} \approx 1{\text{87 m}}$ , 深度估计误差为6.5%。

为避免偶然性, 利用本文所提方法将本次实验中收发距离在9~37 km范围内的声源进行距离估计和深度估计, 图25给出了收发距离在9~37 km范围内的距离估计值、距离估计误差、深度估计值与深度估计误差, 其中以根据爆炸声信号的二次脉动现象推算出的真实声源深度为真实深度值，深度估计误差为真实深度与估计深度之间的相对误差大小。

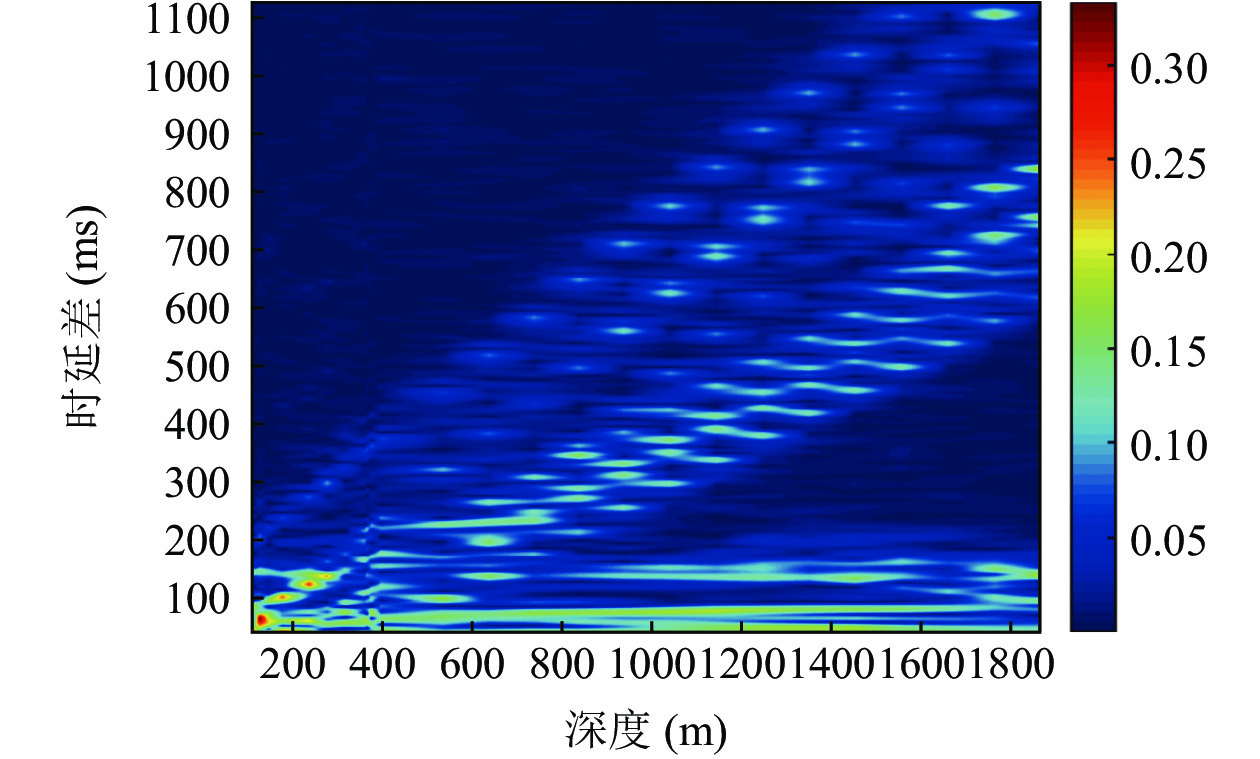
图 25 声源估计结果与实验结果的对比 (a) 距离估计结果; (b) 距离估计误差; (c) 深度估计结果; (d) 深度估计误差

下载: 全尺寸图片幻灯片

从图中可以看出, 当收发距离在10~33 km时, 距离估计结果和深度估计结果都同实际声源距离和深度吻合较好, 估计误差不超过15%; 当收发距离大于33 km时, 距离估计结果不稳定, 深度估计误差也较大, 下面通过声场到达结构分析误差原因。不失一般性, 取水平距离为35 km处的声场, 其时延差值随接收深度的变化结果如图26所示。

图 26 时延差值随接收深度的变化结果

下载: 全尺寸图片幻灯片

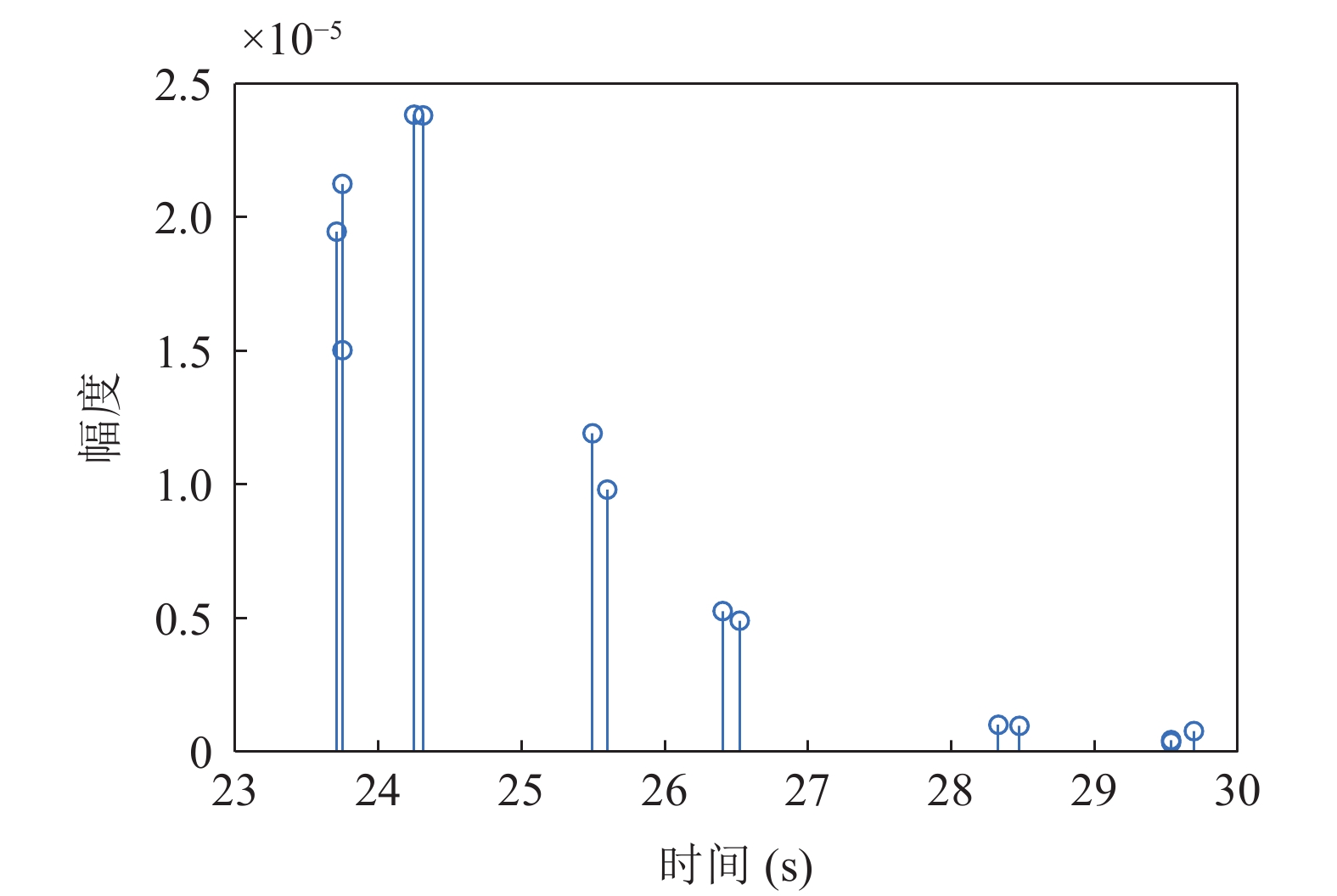
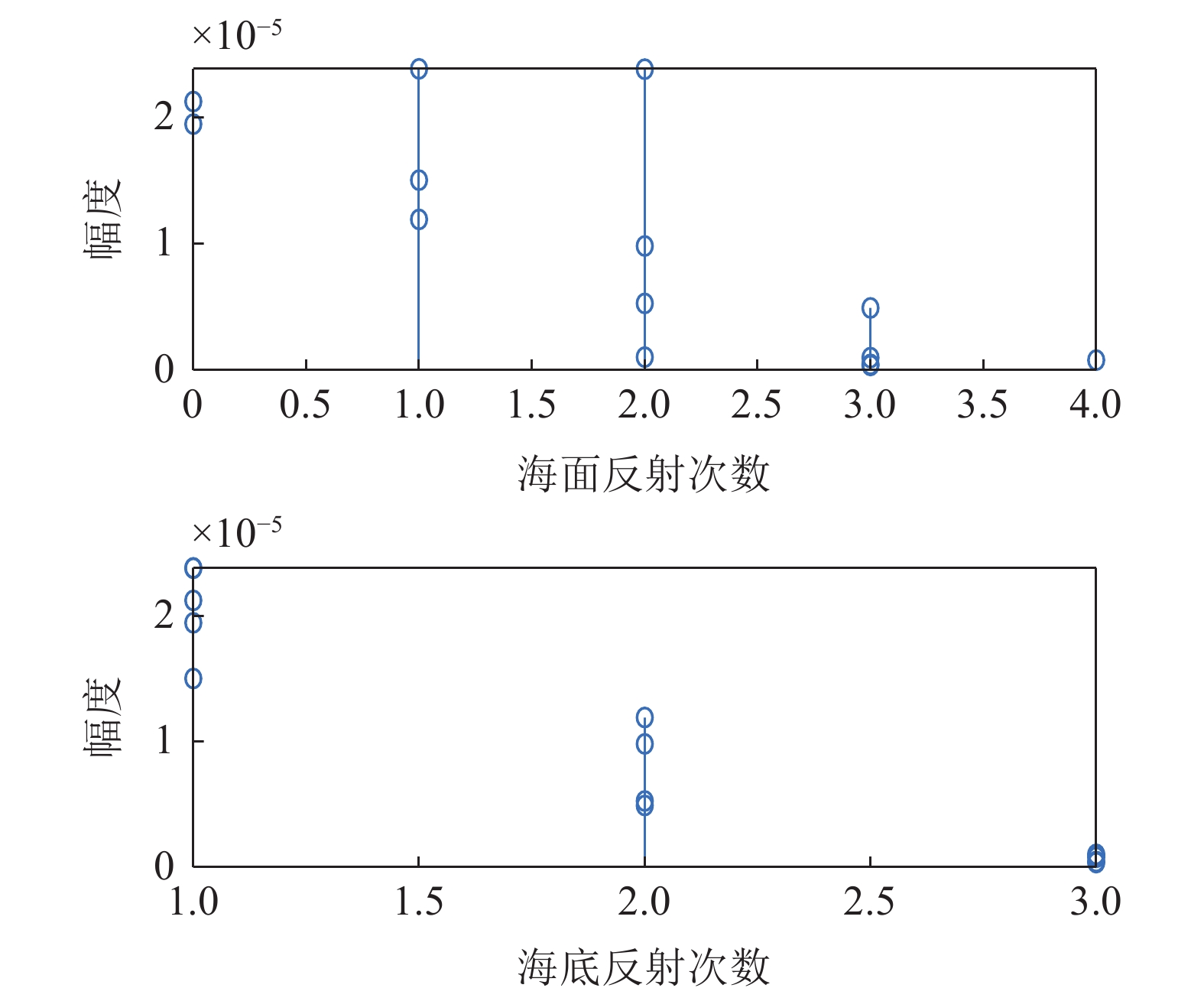
从图26中可以看出, 该声场情况下的时延差值随接收深度的变化曲线不再是6条。图27—图29给出了接收深度为1500 m时的声线到达时间结构、声线反射次数以及声线出射角和入射角。从图中可以看出, 当收发距离较大时, 二次海底反射声线能量不能忽略, 声场不再只由一次海底反射声线构成, 求出的时延差值中包含了二次海底反射声线部分, 时延差结构变得复杂, 利用Radon变换计算的直线斜率误差增大, 从而导致声源距离估计误差增大; 除此之外，声源深度估计结果与距离估计结果和初始时延差值的选取有关, 当时延差结构发生变化后, 初始时延差值的选取也会发生混淆, 使得声源深度的估计误差增大。

图 27 接收深度1500 m时的声线到达时间结构

下载: 全尺寸图片幻灯片

图 28 接收深度1500 m时的声线反射次数

下载: 全尺寸图片幻灯片

图 29 接收深度1500 m时的声线出射角和到达角

下载: 全尺寸图片幻灯片

6. 结论

本文根据深海海底声反射区近海面声源的多途到达结构, 提出了一种利用多途时延差估计深海海底声反射区近海面声源距离和深度的方法。主要结论如下:

(1) 在一定接收深度范围内, 主要构成海底声反射区的4条一次海底反射声线的时延差曲线随接收深度近似呈线性变化。通过推导时延差曲线随接收深度变化的近似表达式, 可以用来估计声源目标的距离和深度。

(2) 仿真实验表明, 当相对阵列孔径为700的情况下，接收信噪比不小于5 dB时, 所提方法能有效估计出声源的水平距离; 接收信噪比不小于8 dB时, 所提方法能有效估计出声源深度, 声源深度的估计误差受初始接收深度的时延差值误差影响要大于距离估计误差的影响。

(3) 南海实验结果表明, 当收发距离在10~33 km时, 距离和深度估计结果都同实际声源距离和深度吻合较好, 估计误差不超过15%, 验证了本文所提方法的有效性。

(4) 与传统的无源测距测深方法相比, 该方法不需要精确的海洋环境参数、提前预知声源的运动状态, 也不需要大规模的拷贝场计算, 具有较好的应用价值。

值得一提的是, 当声场中存在多个声源目标时, 不同声源形成的声线到达结构相互叠加, 会导致该方法的定位性能下降或失效, 有待后续进一步地研究和改善。

图 1 深海典型垂直声速剖面

下载: 全尺寸图片幻灯片

图 2 深海典型声线传播图

下载: 全尺寸图片幻灯片

图 3 深海海底声反射区本征声线结构图

下载: 全尺寸图片幻灯片

图 4 不同阵元经过脉冲压缩的时域接收信号

下载: 全尺寸图片幻灯片

图 5 接收深度2220 m时经过脉冲压缩的时域接收信号

下载: 全尺寸图片幻灯片

图 6 接收深度2220 m时的声线到达时间结构

下载: 全尺寸图片幻灯片

图 7 接收深度2220 m时的声线反射次数

下载: 全尺寸图片幻灯片

图 8 接收深度2220 m时的声线出射角和到达角

下载: 全尺寸图片幻灯片

图 9 时延差值随接收深度的变化结果

下载: 全尺寸图片幻灯片

图 10 基于虚源理论的海底声反射区示意图

下载: 全尺寸图片幻灯片

图 12 时延差值随接收深度的变化结果

下载: 全尺寸图片幻灯片

图 13 Radon变换仿真结果 (a) 参数空间; (b) 恢复图像; (c) 纵向列方差

下载: 全尺寸图片幻灯片

图 14 声源估计结果随接收信噪比的变化关系 (a) 距离估计结果; (b) 深度估计结果

下载: 全尺寸图片幻灯片

图 15 初始时延差值随接收信噪比的变化关系

下载: 全尺寸图片幻灯片

图 17 声源估计结果随相对阵列孔径的变化关系 (a) 距离估计结果; (b) 深度估计结果

下载: 全尺寸图片幻灯片

图 18 声源估计结果随阵元个数的变化关系 (a) 距离估计结果; (b) 深度估计结果

下载: 全尺寸图片幻灯片

图 19 实验海区的垂直声速剖面

下载: 全尺寸图片幻灯片

图 20 实验测得的声传播损失图

下载: 全尺寸图片幻灯片

图 21 归一化接收信号包络

下载: 全尺寸图片幻灯片

图 22 时延差值随接收深度的变化结果

下载: 全尺寸图片幻灯片

图 23 时延差值随接收深度的变化结果 (a) 实验结果; (b) 模型计算结果

下载: 全尺寸图片幻灯片

图 24 Radon变换结果 (a) 参数空间; (b) 恢复图像; (c) 纵向列方差

下载: 全尺寸图片幻灯片

图 25 声源估计结果与实验结果的对比 (a) 距离估计结果; (b) 距离估计误差; (c) 深度估计结果; (d) 深度估计误差

下载: 全尺寸图片幻灯片

图 26 时延差值随接收深度的变化结果

下载: 全尺寸图片幻灯片

图 27 接收深度1500 m时的声线到达时间结构

下载: 全尺寸图片幻灯片

图 28 接收深度1500 m时的声线反射次数

下载: 全尺寸图片幻灯片

图 29 接收深度1500 m时的声线出射角和到达角

下载: 全尺寸图片幻灯片

表 1 不同接收深度对应的4条声线的出射掠射角

接收深度 (m)	${\alpha _{{\text{SBR}}}}$ (°)	${\alpha _{{\text{SBSR}}}}$ (°)	${\alpha _{{\text{BR}}}}$ (°)	${\alpha _{{\text{BSR}}}}$ (°)
200	−26.11	−27.2	24.99	26.12
1000	−24.07	−29.17	22.92	28.12
2000	−21.57	−31.51	20.36	30.52

下载: 导出CSV

参考文献(26)

[1]	Gaul R D, Knobles D P, Shooter J A, et al. Ambient noise analysis of deep-ocean measurements in the Northeast Pacific. IEEE J. Oceanic Eng., 2007; 32(2): 497—512 DOI: 10.1109/JOE.2007.891885
[2]	Yang T C. A method of range and depth estimation by modal decomposition. J. Acoust. Soc. Am., 1987; 82(5): 1736—1745 DOI: 10.1121/1.395825
[3]	Yang T C. Effectiveness of mode filtering: A comparison of matched-field and matched-mode processing. J. Acoust. Soc. Am., 1990; 87(5): 2072—2084 DOI: 10.1121/1.399334
[4]	Bucker H P. Use of calculated sound fields and matched-field detection to locate sound sources in shallow water. J. Acoust. Soc. Am., 1976; 59(2): 368—373 DOI: 10.1121/1.380872
[5]	Fizell R G, Wales S C. Source localization in range and depth in an Arctic environment. J. Acoust. Soc. Am., 1985; 78(S1): S57—S58 DOI: 10.1121/1.2022889
[6]	Tran J Q D, Hodgkiss W S. Matched-field processing of 200-Hz continuous wave (cw) signals. J. Acoust. Soc. Am., 1991; 89(2): 745—755 DOI: 10.1121/1.1894634
[7]	Westwood, Evan K. Broadband matched-field source localization. J. Acoust. Soc. Am., 1992; 91(5): 2777—2789 DOI: 10.1121/1.402958
[8]	周士弘, 张仁和, 龚敏, 等. WKBZ简正波方法在深海匹配场定位中的应用. 自然科学进展, 1997; 7(6): 661—667 DOI: 10.3321/j.issn:1002-008X.1997.06.004
[9]	Hinich M J. Maximum-likelihood signal processing for a vertical array. J. Acoust. Soc. Am., 1973; 54(2): 499—503 DOI: 10.1121/1.1913606
[10]	Shang E C, Wang Y Y. Environmental mismatching effects on source localization processing in mode space. J. Acoust. Soc. Am., 1991; 89(5): 2285—2290 DOI: 10.1121/1.400919
[11]	Richardson A M, Nolte L W. A posteriori probability source localization in an uncertain sound speed, deep ocean environment. J. Acoust. Soc. Am., 1999; 89(5): 2280—2284 DOI: 10.1121/1.400918
[12]	Krolik J L. Matched-field minimum variance beamforming in a random ocean channel. J. Acoust. Soc. Am., 1992; 92(3): 1408—1419 DOI: 10.1121/1.403935
[13]	陈连荣, 彭朝晖, 南明星. 高斯射线束方法在深海匹配场定位中的应用. 声学学报, 2013; 38(6): 715—723 DOI: 10.15949/j.cnki.0371-0025.2013.06.020
[14]	Baggeroer A B, Scheer E K, Heaney K, et al. Reliable acoustic path and convergence zone bottom interaction in the Philippine Sea 09 Experiment. J. Acoust. Soc. Am., 2010; 128(4): 2385 DOI: 10.1121/1.3508530
[15]	Tiemann C O, Thode A M, Straley J, et al. Three-dimensional localization of sperm whales using a single hydrophone. J. Acoust. Soc. Am., 2006; 120(4): 2355—2365 DOI: 10.1121/1.2335577
[16]	Li H, Xu Z Z, Yang K D, et al. Use of multipath time-delay ratio for source depth estimation with a vertical line array in deep water. J. Acoust. Soc. Am., 2021; 149(1): 524—539 DOI: 10.1121/10.0003364
[17]	李辉. 深海大深度声场特性与目标定位技术研究. 博士学位论文, 西安: 西北工业大学, 2017
[18]	Duan R, Yang K D, Ma Y L, et al. Moving source localization with a single hydrophone using multipath time delays in the deep ocean. J. Acoust. Soc. Am., 2014; 136(2): 159—165 DOI: 10.1121/1.4890664
[19]	Lei Z X, Yang K D, Ma Y L. Passive localization in the deep ocean based on cross-correlation function matching. J. Acoust. Soc. Am., 2016; 139(6): 196—201 DOI: 10.1121/1.4954053
[20]	Wu J N, Zhou S H, Peng Z H, et al. Bearing splitting and near-surface source ranging in the direct zone of deep water. Chin. Phys. B, 2016; 25(12): 81—88 DOI: 10.1088/1674-1056/25/12/124311
[21]	孙梅, 周士弘. 大深度接收时深海直达波区的复声强及声线到达角估计. 物理学报, 2016; 65(16): 134—143 DOI: 10.7498/aps.65.164302
[22]	高飞, 孙磊. 基于首达波与次达波到达时差的深海浅层移动声源定位. 兵工学报, 2018; 39(11): 2243—2248 DOI: 10.3969/j.issn.1000-1093.2018.11.019
[23]	王梦圆, 李整林, 吴双林, 等. 深海大深度声传播特性及直达声区水下声源距离估计. 声学学报, 2019; 44(5): 905—912 DOI: 10.15949/j.cnki.0371-0025.2019.05.011
[24]	王梦圆, 李整林, 秦继兴, 等. 深海直达声区水下声源距离深度联合估计. 信号处理, 2019; 35(9): 1535—1543 DOI: 10.16798/j.issn.1003-0530.2019.09.011
[25]	谢亮, 王鲁军, 林旺生. 深海脉冲信号簇到达结构特征及其在水下声源定位中的应用. 声学学报, 2021; 46(2): 171—181 DOI: 10.15949/j.cnki.0371-0025.2021.02.002
[26]	刘炎堃, 郭永刚, 李整林, 等. 基于路径选择的深海水下运动目标被动深度估计. 应用声学, 2020; 39(5): 647—655 DOI: 10.11684/j.issn.1000-310X.2020.05.001

施引文献(4)

期刊类型引用(4)

1.	刘与涵，郭良浩，董阁，章伟裕，徐嘉璘，徐鹏，刘建军，任岁玲，屈嵩岳. 深海移动水平阵声源被动定位方法研究进展. 应用声学. 2025(01): 36-54 . 百度学术
2.	谢其宸，迟骋，张博，黄海宁. 利用海底反射时延结构的深海海底反射区目标距离深度估计方法. 声学学报. 2024(04): 627-635 . 本站查看
3.	XIE Qichen，CHI Cheng，ZHANG Bo，HUANG Haining. A range and depth estimation method using the time delay structure of bottom reflection in deep sea bottom bounce area. Chinese Journal of Acoustics. 2024(03): 275-289 . 必应学术
4.	白宗龙，张君燕，刘成刚. 一种面向高分辨率声学成像的频带加权方法. 仪器仪表学报. 2024(10): 253-262 . 百度学术

其他类型引用(0)

资源附件(0)

图(29) / 表(1)

计量

文章访问数: 344
HTML全文浏览量: 31
PDF下载量: 69
被引次数: 4

引言
1. 海底声反射区多途时延到达结构分析
2. 定位原理及仿真研究
3. 基于Radon变换的改进定位方法
4. 影响因素分析
4.1 接收信噪比
4.2 等效声速
4.3 阵列孔径
5. 实验数据验证
6. 结论

深海海底声反射区多途时延差分析与近海面声源定位

作者简介: 徐嘉璘, xujialin@mail.ioa.ac.cn

通讯作者: 郭良浩, glh2002@mail.ioa.ac.cn

计量

出版历程

Analysis of multipath time delay difference in deep ocean bottom bounce area and its application in near-surface target location

引言

1. 海底声反射区多途时延到达结构分析

2. 定位原理及仿真研究

3. 基于Radon变换的改进定位方法

4. 影响因素分析

4.1 接收信噪比

4.2 等效声速

4.3 阵列孔径

5. 实验数据验证

6. 结论

期刊类型引用(4)

其他类型引用(0)

计量

出版历程

目录

引言

1. 海底声反射区多途时延到达结构分析

2. 定位原理及仿真研究

3. 基于Radon变换的改进定位方法

4. 影响因素分析

4.1 接收信噪比

4.2 等效声速

4.3 阵列孔径

5. 实验数据验证

6. 结论

作者简介:
徐嘉璘, xujialin@mail.ioa.ac.cn

通讯作者:
郭良浩, glh2002@mail.ioa.ac.cn