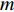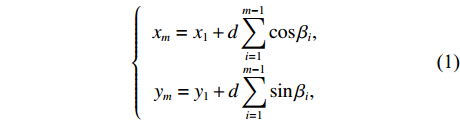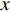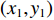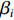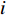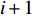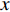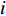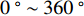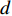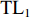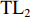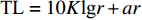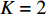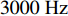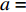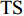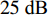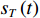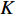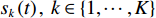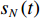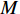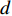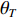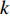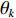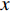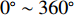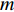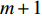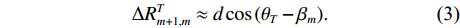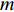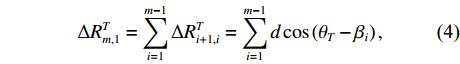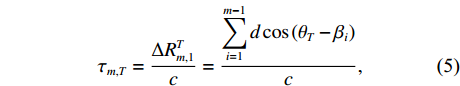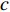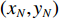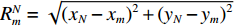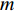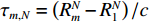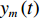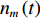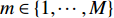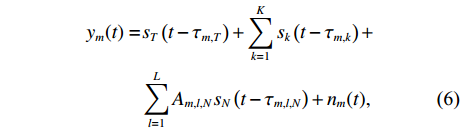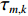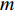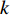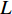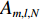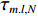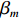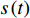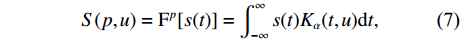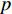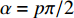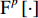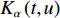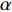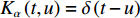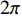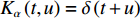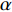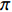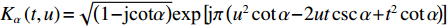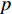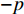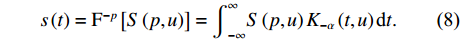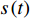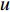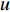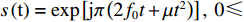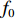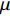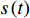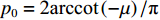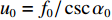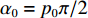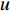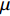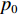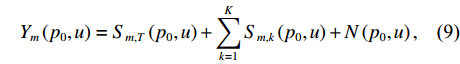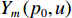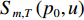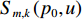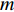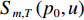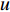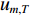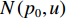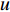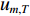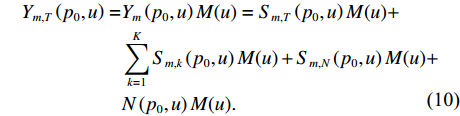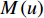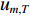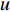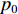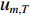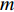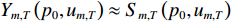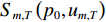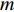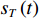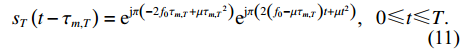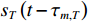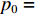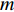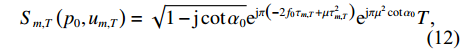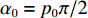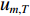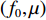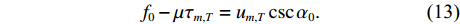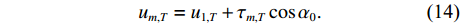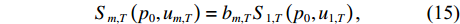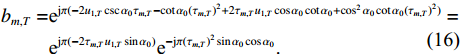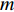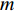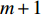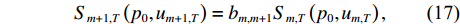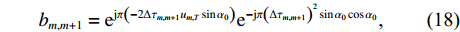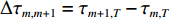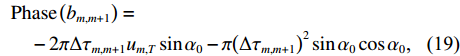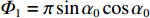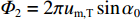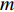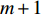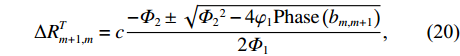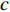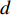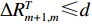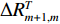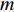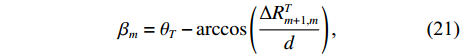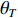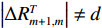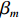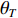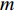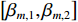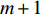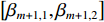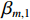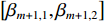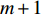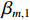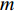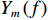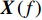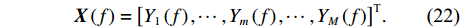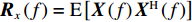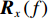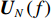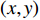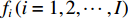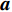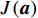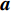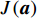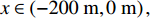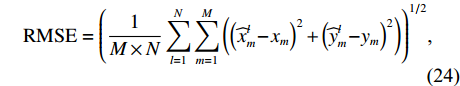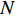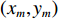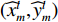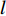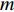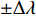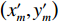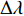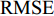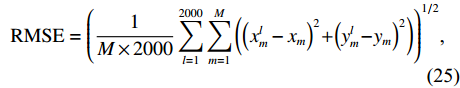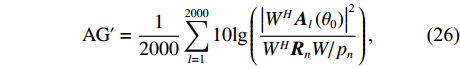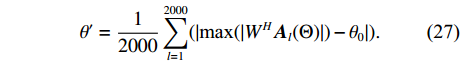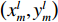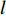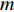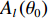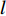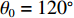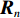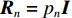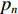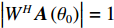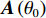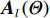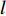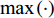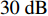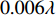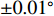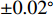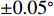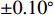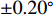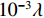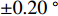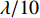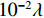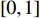Real-time calibration method of flexible horizontal array for bistatic active detection
-
摘要:
双基地有源模式下接收基地搭载的柔性水平阵在运动过程中, 阵形会发生实时的畸变。针对阵形误差的存在会严重影响水听器阵列探测性能的问题, 本文提出一种基于发射信号为线性调频(LFM)信号, 利用直达波实现阵形参数估计的方法。该方法首先利用分数阶傅里叶变换(FRFT)对LFM信号在特定阶数的分数阶傅里叶变换域上的能量聚集性, 实现直达波与目标回波的分离, 避免了目标回波对于阵形参数估计的影响。而后利用各阵元直达波FRFT后对应峰值点之间的相位差实现了阵形参数估计, 并提出了一种基于拖曳船辐射噪声的阵形解模糊方法。计算机仿真表明该方法对于噪声及干扰影响、入射角度误差以及多普勒频移均有一定的宽容性, 湖上实验验证了阵形估计方法的有效性, 是一种可实时校准、高精度、稳健的柔性水平阵阵形估计算法。
Abstract:The flexible horizontal array carried by the receiving base in the bistatic base of active mode has real-time array shape distortion during the motion. The detection performance of hydrophone arrays is seriously affected by the existence of array shape errors. A method is proposed in this paper to estimate the array shape parameters using direct waves based on LFM signal to solve the problem. In the method, the FRFT is firstly used to separate the direct wave from the target echo, avoiding the influence of the target echo on the array parameter estimation. The phase difference between the corresponding peak points after FRFT of each array element is used to estimate the array parameters, and an array deblurring method based on the radiation noise of the towing vessel is proposed. Computer simulation shows that the method is tolerant to noise and interference effects, incident angle errors and Doppler shifts. The effectiveness of the array estimation method is verified by the experiments on the lake, which is a flexible horizontal array estimation algorithm that can be calibrated in real time with high accuracy and robustness.
-
Keywords:
- Bistatic base /
- Active detection /
- Array calibration /
- Fractional Fourier transform
-
引言
随着潜艇隐身技术的发展, 低频、大孔径的拖曳阵受到了广泛关注[1]。在过去的十几年里, 多基地声呐系统由于其配置方式灵活、隐蔽性强、探测范围大等优点受到广泛关注, 多基地模式下的拖曳声呐逐渐成为反潜探测的重要手段[2]。这种声呐不受平台尺寸的限制, 搭载方式灵活, 但在拖曳过程中不可避免地会受到拖船运动、海流等实时因素的影响, 导致阵形发生畸变[3]。而在实际应用中常常假设拖曳阵阵形始终为一条直线, 使得拖曳阵探测目标的能力降低, 因此迫切需要一种可实现多基地模式下拖曳阵阵形参数实时校准的方法。
目前拖曳阵阵形参数估计方法可分为两大类, 第一类是利用非声学的方法进行估计[4-7]: 在拖曳阵各段加入姿态传感器, 利用不同位置处的姿态信息估计出阵列阵形, 或对拖曳阵的受力状态进行力学建模, 通过求解力学方程估计拖曳阵的阵形。这类方法虽然能实时获取阵形姿态信息, 不过需要在拖曳阵上大量加装非声传感器, 硬件设计难度大, 阵列可靠性下降, 同时其估计效果受传感器数量和精度限制、流体动力学校准算法的准确性等因素影响较大。第二类算法是基于声学的方法估计阵形[8-15], 可分为自校正算法和有源校正算法。其中自校正算法中将校正源方位看作未知参数[8-9], 通过构造优化函数将阵列误差和信源方位进行联合优化求解, 同时得到信源方位和阵形估计结果, 可适用于多基地模式下的拖曳阵阵形校准, 但拖曳阵阵元数较多, 自校正方法的迭代过程计算量过大, 难以及时得到阵形校准结果。有源校正算法是通过人为在空间中放置方位或位置已知的校正声源, 对阵列接收的信号进行后置处理从而实现阵形参数估计的方法。梁国龙等通过构造阵元位置模型, 利用入射声源信号与阵元位置的对应关系实现阵形估计[10-12], 该方法的估计精度与阵元位置误差及其建模的合理性、校正声源信息获取的实时性和声传播特性相关, 在构造阵元位置模型时仅考虑在理论位置的基础上小的偏移从而简化位置模型, 对于拖曳阵来说, 实际工作中阵形畸变程度较大, 位置模型与实际吻合程度不高。Brian等提出了特征矢量法, 通过对接收信号的协方差矩阵进行特征分解, 得到校正声源方向的特征矢量, 进而实现阵形校准, 又针对宽带声源提出了分子带的特征矢量方法[13-14]。但特征矢量法是基于单校正声源的情况, 存在其他方向的来波干扰时, 其参数估计性能降低。汪俊等提出了一种利用双声源对阵形参数进行估计的算法[15], 需要两个方位已知声源, 而在拖曳阵实际工作的条件下, 难以满足设置双校正声源的条件。目前有源校正方法主要应用于校正源与目标位置相对固定, 阵形畸变较小的情况, 对于运动的拖曳阵来说, 难以满足其时变阵形的校准需求。收发分置的双基地声呐系统中, 发射信号广泛采用多普勒宽容性良好的LFM信号作为探测信号, 同时一般会选择增大信号脉宽以获得更高的时间增益[16], 但长脉宽信号会增大直达波的掩蔽区域, 导致其与目标回波时域上部分重叠。若利用直达波进行校准, 目标回波干扰是影响校正算法的重要因素。
上述估计阵形参数的方法中, 非声学方法受非声传感器数量及精度等因素的限制, 阵元位置参数估计有效性和准确度难以实时掌握; 声学方法对于双基地有源模式下阵元数较多的拖曳阵来说, 自校正方法计算量过大, 有源校正方法难以配备合作校正源, 且缺少相干干扰抑制算法, 难以实现准确、实时的阵元位置参数估计。在双基地有源模式下, 发射基地和接收基地的位置已知, 此时发射基地相当于一个位置已知的校正声源, 在每个发射周期内可实现对接收基地的拖曳阵阵形校准, 发射周期较短时, 当前周期其他时刻的阵形与校准时刻阵形接近。基于这一假设, 本文提出了一种利用直达波对阵形参数实时校准的方法。介绍了柔性水平阵阵列接收信号模型; 针对可能存在的回波干扰, 提出了一种基于FRFT的直达波提取算法, 并在直达波提取的基础上给出了阵元位置参数估计算法; 针对估计阵形的双解问题, 利用拖曳船辐射噪声在两阵形下近场空间谱强度的差异, 实现了模糊阵形的辨识。计算机仿真验证表明本文算法精度较高, 不受目标回波的影响, 对于校正声源的入射角度误差和多普勒频移均具有良好的宽容性。在实际湖上实验数据处理中, 该算法被证明可实现干扰的剔除, 并在阵形校准后提高目标回波的估计精度。
1. 柔性水平阵及阵列信号模型
1.1 柔性水平阵模型
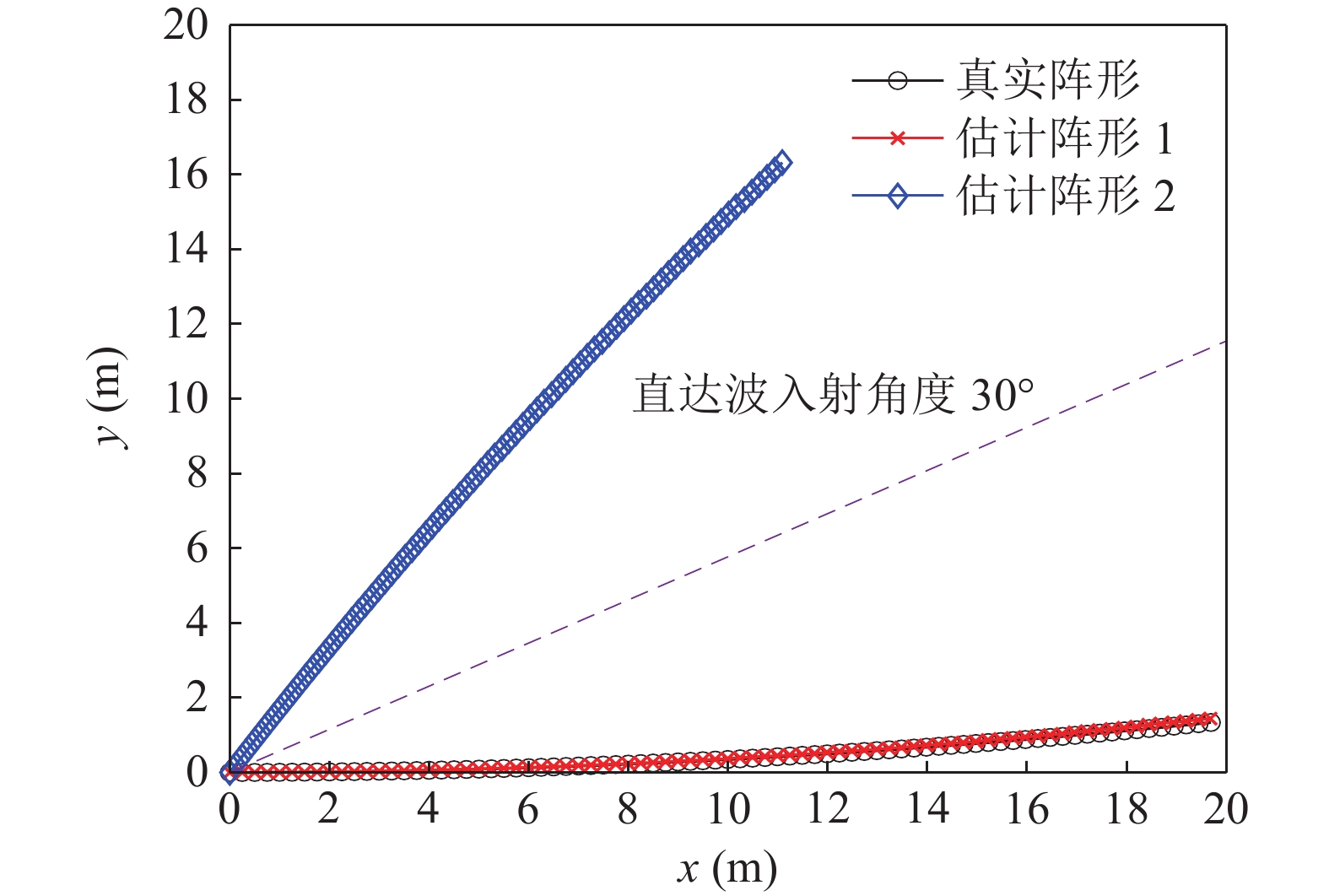
本节介绍了柔性水平阵模型, 假设该模型由
M 元等间距的水听器组成。在拖曳船机动过程中, 拖曳船航速远大于海流速度时, 发生畸变的阵形可近似为抛物线形或圆弧形[5,17], 阵列会保持平滑的形状[8], 各相邻阵元的航向角应为连续变化。图1展示了该柔性水平阵发生畸变时示意图, 其中红线为柔性水平阵的默认阵形(一条直线), 蓝线为实际工作中受到船舶机动、洋流等因素影响导致柔性水平阵可能发生的畸变。柔性水平阵充分展开状态下, 相邻阵元之间的间距可以被认为是固定的, 利用该性质可以得到同一时刻内第
m 个阵元坐标的表达式[7,8,18]:{xm=x1+dm−1∑i=1cosβi,ym=y1+dm−1∑i=1sinβi, (1) 其中,
x 轴正方向为拖曳船航向的反方向,(x1,y1) 为当前时刻的首阵元坐标, 在柔性水平阵示意图中被认为原点,βi 为当前时刻第i 阵元与第i+1 阵元的连线与x 轴正方向逆时针夹角, 被称为第i 阵元的航向角, 角度范围为0 ∘∼360 ∘ ,d 为相邻阵元间距, 式(1)表明同一时刻内, 阵元坐标只与首阵元坐标以及前序各阵元处的航向角有关。1.2 阵列信号模型
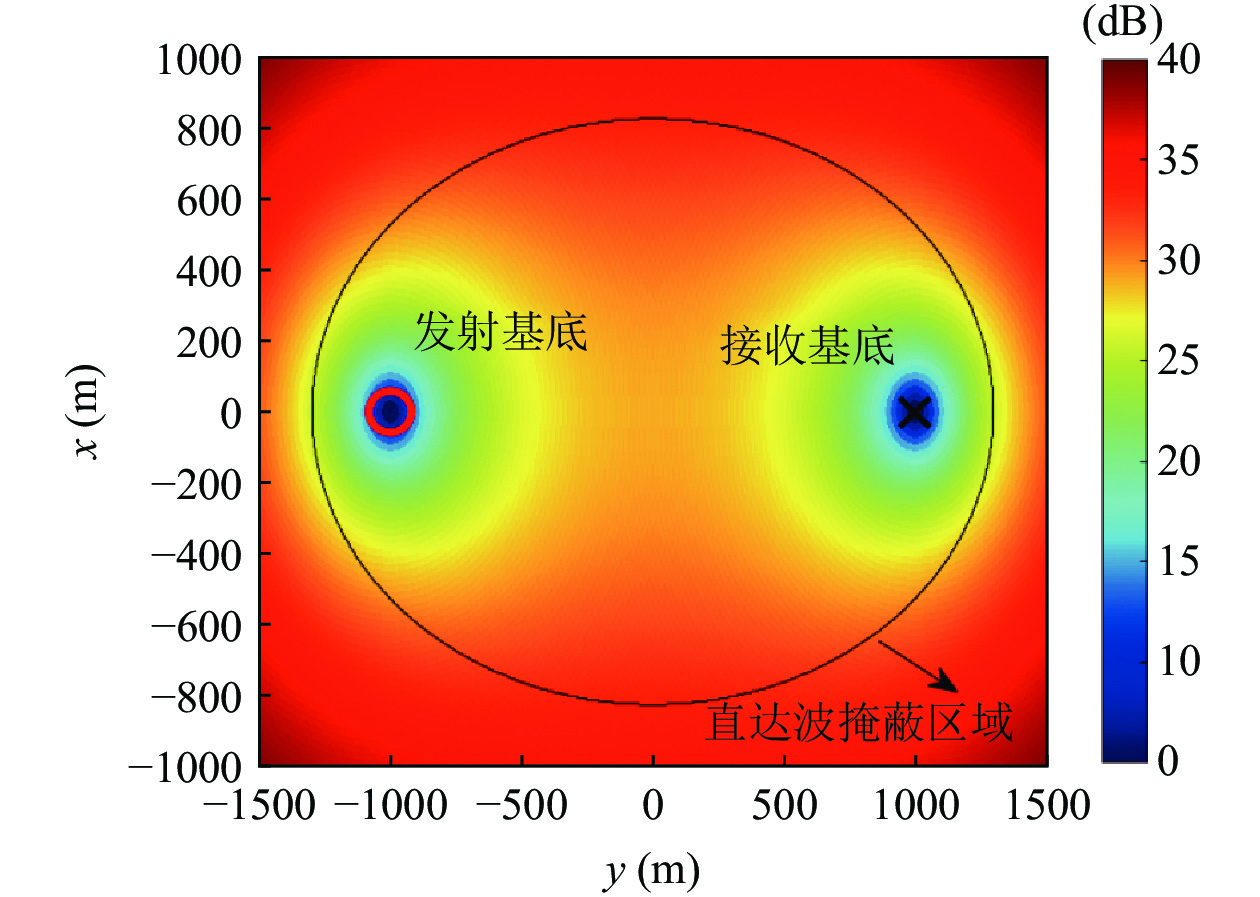
对于收发分置的双基地声呐系统来说, 接收基地会收到未经目标反射的直达波、探测目标的回波以及拖曳船的本地辐射噪声[19], 当目标回波前沿到达时刻早于直达波后沿到达时刻与发射信号脉宽之和时, 直达波与目标回波在时域上会部分重叠, 对后续利用直达波进行阵形参数估计产生影响。下面将对直达波的掩蔽效果进行仿真分析, 将目标回波视为干扰, 计算目标在不同位置处时直达波与目标回波在接收基地处的信干比, 信干比表达式如下:
SIR=−TL+TL1+TL2−TS, (2) 其中,
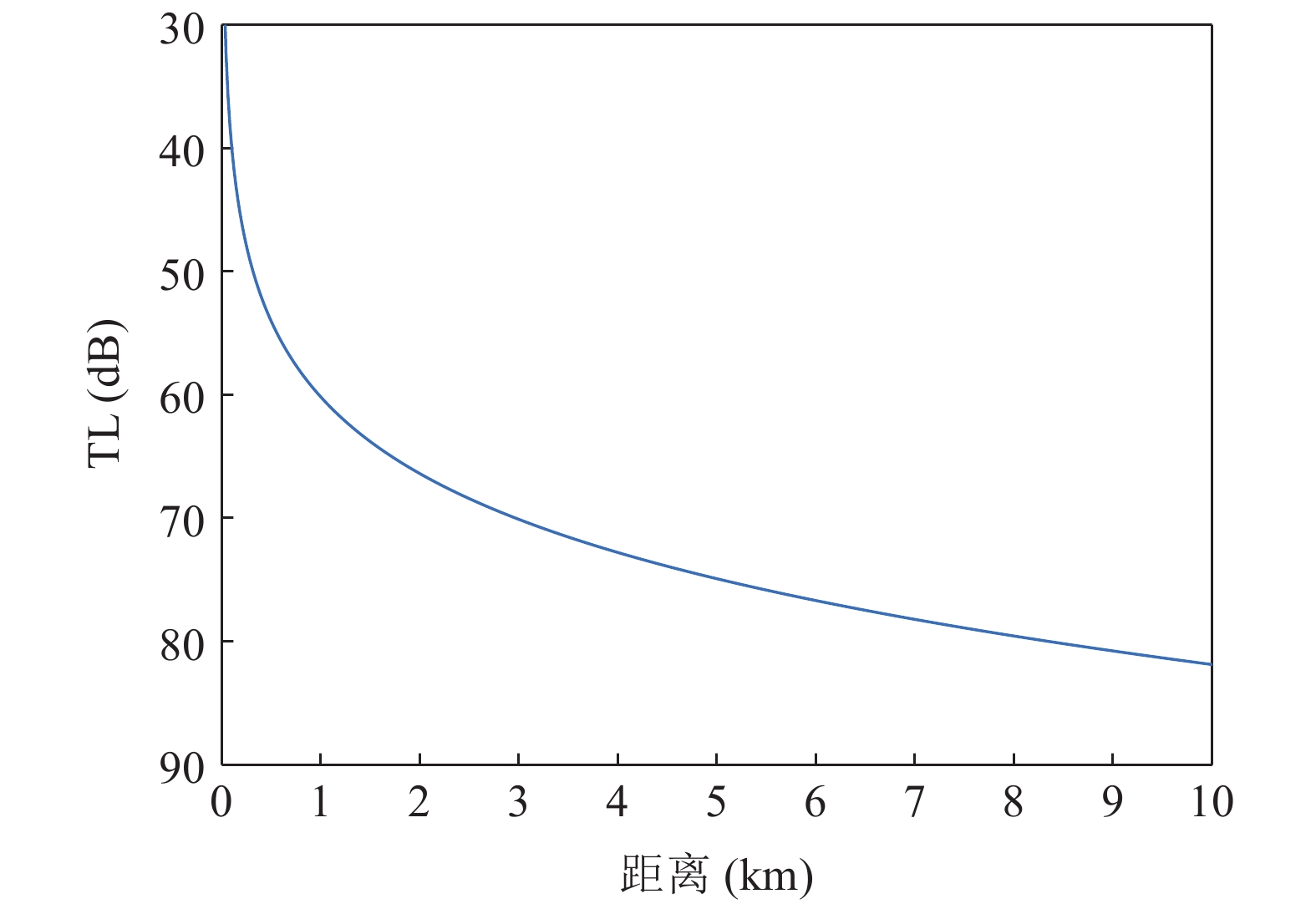
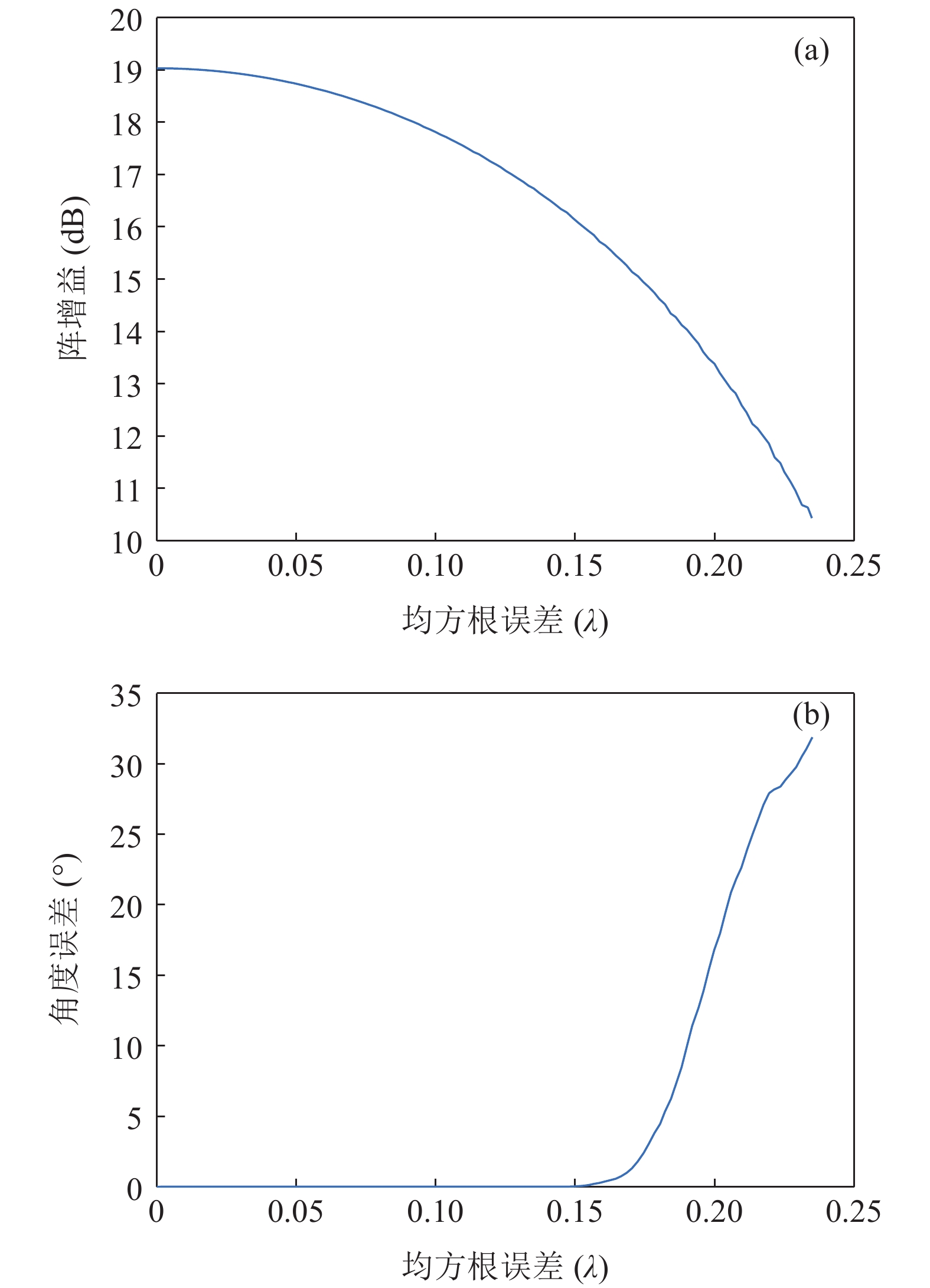
TL 为直达波的传播损失,TL1 为发射基地至目标处的传播损失,TL2 为目标至接收基地处的传播损失, 可利用传播损失方程TL=10Klgr+ar 粗略估算不同传播距离处的传播损失, 其中考虑球面扩展时K=2 , 海水吸收系数在中心频率为3000 Hz 时,a=0.1871 dB/km [20],TS 为目标强度, 假设为25 dB [21]。利用传播损失方程得到不同传播距离处的传播损失如图2所示。图3为双基地声呐系统的俯视图, 图中各点处的色棒值代表着目标在当前位置时接收基地处直达波与目标回波的信干比。信号脉宽为0.4 s时, 当目标位于椭圆黑线内, 目标回波与直达波存在时域重叠, 该区域被称为直达波掩蔽区域。从图3可以看出, 在直达波掩蔽区域内, 直达波作为信号, 目标回波作为干扰, 直达波与目标回波的信干比基本小于30 dB, 当目标位于发射基地和接收基地附近时, 直达波与目标回波的信干比最低, 在3.2节中分析了直达波掩蔽区域内信干比在5~30 dB区间内变化对于阵形估计的影响。
考虑直达波信号为
sT(t) , 存在K 个目标回波信号sk(t), k∈{1,⋯,K} , 拖曳船辐射噪声为sN(t) , 入射到阵元数为M 、相邻阵元间距为d 的等间距柔性水平阵上。直达波的入射角度为θT , 第k 个目标回波信号的入射角度为θk , 如图1所示, 入射角度表示与x 轴正方向逆时针夹角, 角度范围为0∘∼360∘ 。以直达波为例, 依据1.1节中所提柔性水平阵模型可得到第m 个阵元与第m+1 个阵元的声程差为ΔRTm+1,m≈dcos(θT−βm). (3) 假设以首阵元为参考点, 第
m 个阵元与参考点的声程差为ΔRTm,1=m−1∑i=1ΔRTi+1,i=m−1∑i=1dcos(θT−βi), (4) 则相应的时延量为
τm,T=ΔRTm,1c=m−1∑i=1dcos(θT−βi)c, (5) 其中,
c 为声波在水中的传播速度。拖曳船辐射噪声为近场声源, 声源位置为
(xN,yN) , 声源到各个阵元的距离为RNm=√(xN−xm)2+(yN−ym)2 , 以首阵元为参考点, 第m 个阵元与参考点的时延量为τm,N=(RNm−RN1)/c 。柔性水平阵各阵元输出用
ym(t) 表示,nm(t) 为各接收阵元的加性噪声干扰, 其中,m∈{1,⋯,M} , 则阵列接收信号可写为ym(t)=sT(t−τm,T)+K∑k=1sk(t−τm,k)+L∑l=1Am,l,NsN(t−τm,l,N)+nm(t), (6) 其中, 第1项为直达波; 第2项为目标回波,
τm,k 为第m 个阵元与参考点对于第k 个目标回波的时延差, 计算方法同直达波; 第3项为拖曳船辐射噪声,L 表示多径传播的声线个数,Am,l,N 为幅度,τm.l,N 为时间延迟。2. 基于FRFT的阵形参数估计方法
阵列接收信号中包含着阵形参数(阵元航向角
βm ), 直达波的入射角度可由发射、接收基地相对位置得到, 因此可以利用直达波作为校准源实现阵形参数的估计。针对可能存在的目标回波干扰, 利用LFM信号在分数阶域的能量聚集性实现直达波与回波的分离, 下文将提出一种利用FRFT实现直达波提取与阵形参数估计的方法。2.1 FRFT方法概述
分数阶傅里叶变换是傅里叶变换的一种广义形式, 信号的FRFT可以理解为信号在时频平面上绕坐标轴逆时针旋转[22], 信号
s(t) 的FRFT定义为S(p,u)=Fp[s(t)]=∫∞−∞s(t)Kα(t,u)dt, (7) 其中,
p 为FRFT的阶数, 可以为任意实数,α=pπ/2 ,Fp[⋅] 为FRFT的算子符号,Kα(t,u) 为FRFT的变换核。当α 是2π 的倍数时,Kα(t,u)=δ(t−u) ; 当α+π 是2π 的倍数时,Kα(t,u)=δ(t+u) ; 当α 不是π 的倍数时,Kα(t,u)=√(1−jcotα)exp[jπ(u2cotα−2utcscα+t2cotα)] 。FRFT是一种酉变换,p 阶FRFT的逆变换为−p 阶FRFT,s(t)=F−p[S(p,u)]=∫∞−∞S(p,u)K−α(t,u)dt. (8) 式(8)说明, 信号
s(t) 可被分解为u 域上一组正交LFM基的线性组合,u 域一般被称为分数阶傅里叶变换域。LFM信号在合适的FRFT域中具有能量聚集特性, 即形成一个冲激函数, 利用这一特性可以实现LFM信号的提取。LFM信号可表示为
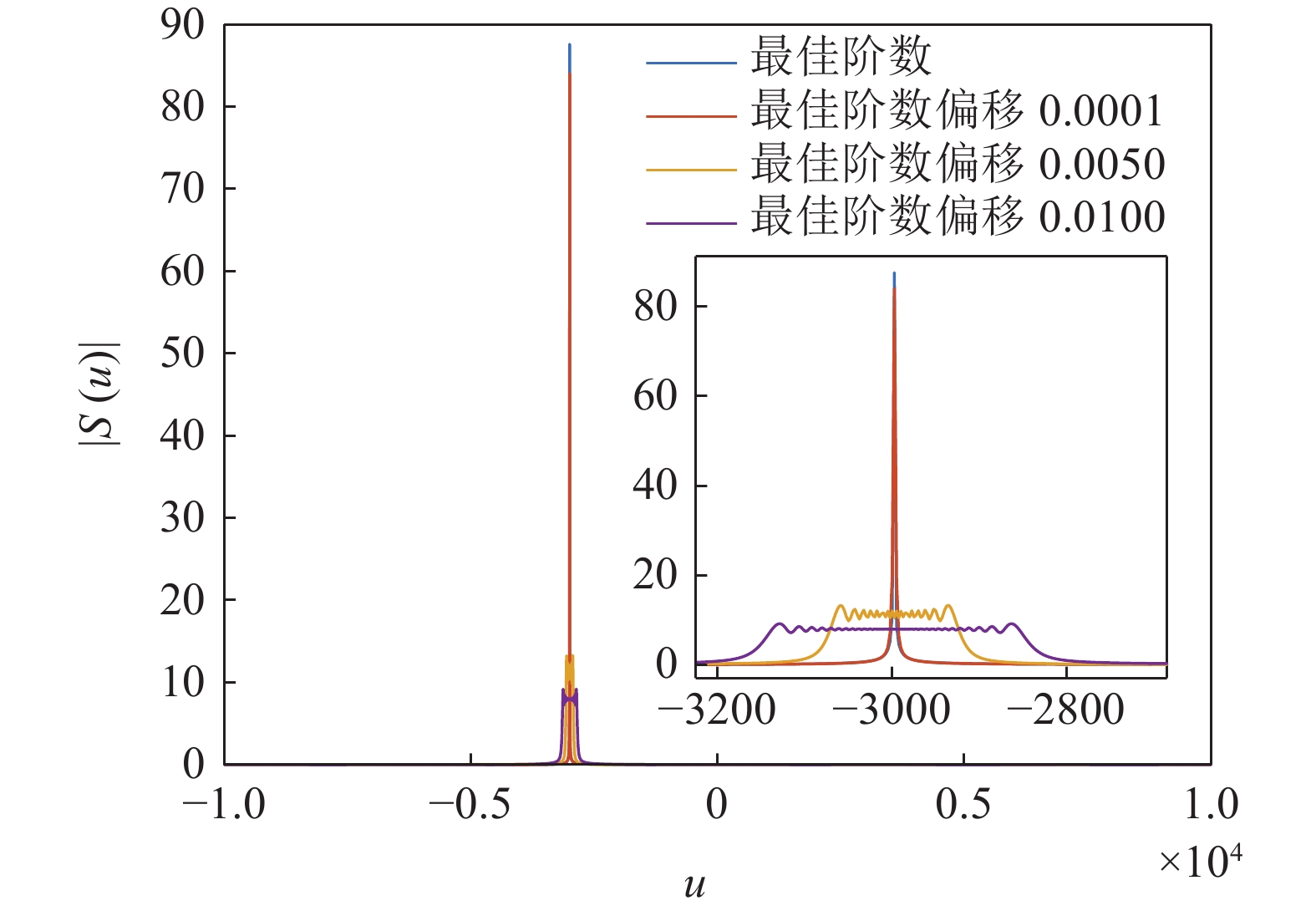
s(t)=exp[jπ(2f0t+μt2)], 0⩽ ,其中{f_0} 为初始频率,\mu 为调频斜率。信号s\left( t \right) 在{p_0} = 2{\text{arccot}}\left( { - \mu } \right)/{\text{π }} 阶的FRFT上, 以{u_0} = {f_0}/ \csc{\alpha _0} 为中心的窄带内具有最佳的能量聚焦特性,{\alpha _0} = {p_0}\pi /2 。图4展示了LFM信号在最佳阶数和非最佳阶数上的分数阶傅里叶变换, 该信号参数为脉宽0.4 s, 带宽500 Hz, 中心频率3000 Hz。从图中可以看出LFM信号在最佳阶数的FRFT上具有最佳的能量聚集特性, 随着FRFT变换阶数逐渐远离最佳阶数, 信号在FRFT域形成的峰值逐渐降低, 宽度逐渐增大, 可以利用FRFT对LFM信号的能量聚集特性实现后续的直达波信号提取与阵形参数估计。2.2 直达波信号提取算法
由2.1节可知, LFM信号可通过特定阶数的FRFT达到能量最佳聚集效果。直达波与回波的能量会集中在
u 域上以其各自峰值点为中心的一个窄带内, 利用这一特点可实现各阵元信号的直达波的提取。提取步骤如下:(1) 由发射信号参数得到FRFT的最佳聚焦阶数
{p_0} = 2{\text{arccot}}\left( { - \mu } \right)/{\text{π }} , 其中\mu 为发射信号的调频斜率。(2) 对各阵元接收信号(式(6))进行
{p_0} 阶的FRFT, 得到变换后的信号表示为Y_m\left(p_0, u\right)=S_{m, T}\left(p_0, u\right) + \sum_{k=1}^K S_{m, k}\left(p_0, u\right) + N\left(p_0, u\right), (9) 其中,
{Y_m}\left( {{p_0},u} \right) ,{S_{m,T}}\left( {{p_0},u} \right) ,{S_{m,k}}\left( {{p_0},u} \right) 分别为第m 个阵元的接收信号、直达波信号以及回波信号的FRFT,{S_{m,T}}\left( {{p_0},u} \right) 的能量绝大部分集中在u 域上以{u_{m,T}} 为中心的一个窄带内。N\left( {{p_0},u} \right) 为噪声的FRFT, 一般不会出现聚集特性。(3) 在
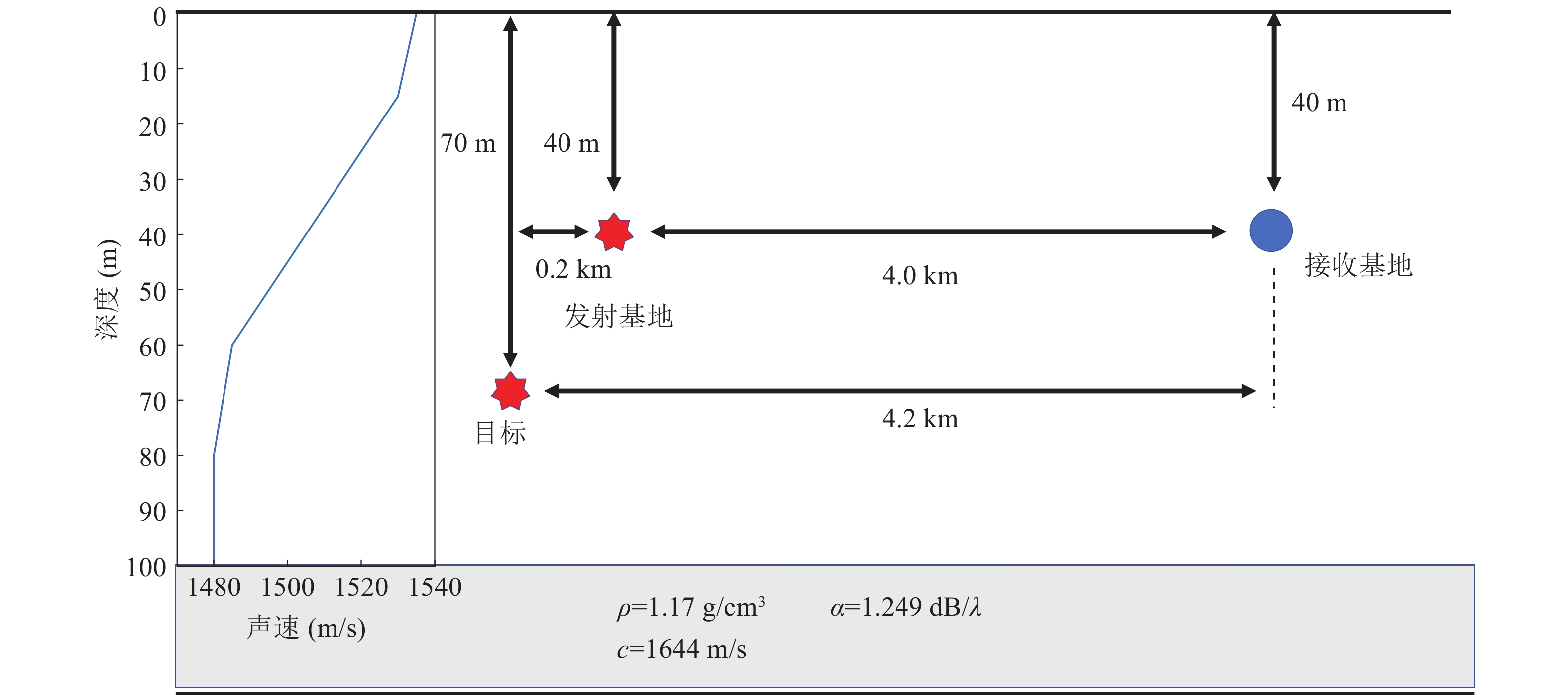
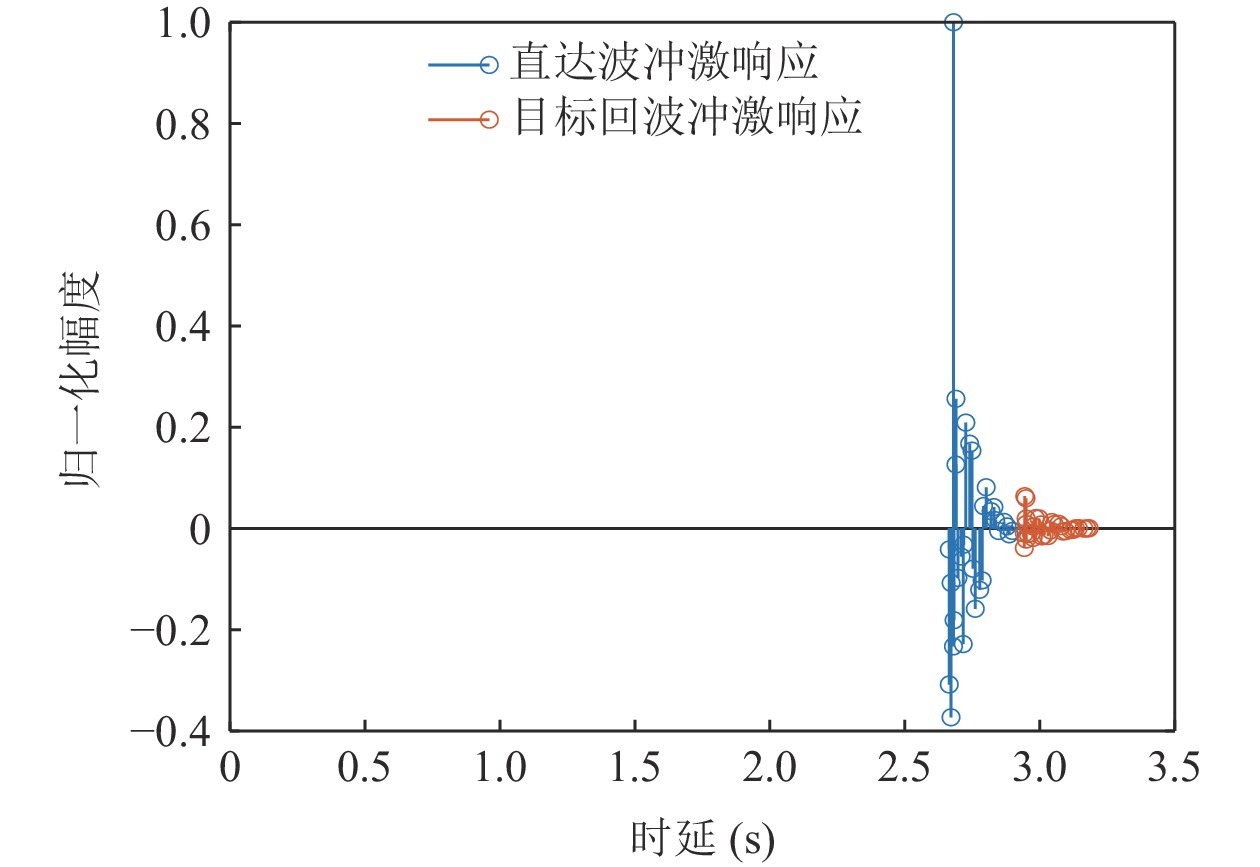
u 域内对以{u_{m,T}} 为中心的窄带之外的区间置零, 即\begin{split} Y_{m, T}\left(p_0, u\right)=&Y_m\left(p_0, u\right) M(u)=S_{m, T}\left(p_0, u\right) M(u) + \\&\sum_{k=1}^K S_{m, k}\left(p_0, u\right) M(u) + S_{m, N}\left(p_0, u\right) M(u) + \\&N\left(p_0, u\right) M(u) .\\[-12pt] \end{split} (10) M\left( u \right) 为中心频率为{u_{m,T}} 的时变u 域带通滤波器, 适当选择其带宽, 经过u 域内的带通滤波后可保留直达波的能量并且去除掉回波以及绝大部分的噪声能量。针对本节提出的直达波信号的提取算法在信道仿真背景下进行验证, 仿真实验中环境参数以及发射、接收基地与目标间相对位置如图5所示, 目标强度为25 dB, 发射信号为脉宽0.4 s、带宽500 Hz、中心频率3000 Hz的LFM信号。利用Bellhop实现对直达波以及目标回波传播信道的仿真, 得到的直达波与目标回波的信道冲激响应如图6所示。FRFT域内直达波与目标回波的信号分离能力如图7所示。仿真结果说明FRFT可以实现直达波与目标回波的分离, 并利用
u 域带通滤波器在FRFT域内实现对直达波的提取。2.3 阵形参数估计算法
参数估计的步骤紧跟直达波提取算法, 由双基地声呐的发射基地与接收基地的相对位置及拖曳船航向可得直达波的入射角度, 此时将阵形参数估计的问题转变为利用方位已知的单声源发射固定参数的LFM信号对柔性水平阵阵形参数进行实时估计的问题。在对直达波和目标回波信号分离的基础上, 本文进一步研究提出了一种基于FRFT的阵形参数估计方法。
经过直达波提取后的信号如式(10)所示, 各阵元信号直达波的能量大部分都集中在
{p_0} 阶FRFT对应的峰值点处,{u_{m,T}} 为第m 个阵元直达波所对应的峰值点位置, 可得{Y_{m,T}}\left( {{p_0},{u_{m,T}}} \right) \approx {S_{m,T}}\left( {{p_0},{u_{m,T}}} \right) 。下面将推导各阵元峰值点{S_{m,T}}\left( {{p_0},{u_{m,T}}} \right) 之间的关系实现阵形参数估计。由式(6)可得, 当发射信号为LFM信号时, 第
m 个阵元接收到的直达波{s_T}\left( t \right) 为{s}_{T}\left(t-{\tau }_{m,T}\right)={\rm e}^{{\rm{j}}\pi \left(-2{f}_{0}{\tau }_{m,T} + \mu {\tau }_{m,T}{}^{2}\right)}{\rm e}^{{\rm{j}}\pi \left(2\left({f}_{0}-\mu {\tau }_{m,T}\right)t + \mu {t}^{2}\right)}\text{, }\;\;0\leqslant t\leqslant T. (11) 由2.1节可知,
{s_T}\left( {t - {\tau _{m,T}}} \right) 在FRFT阶数{p_0} = 2{\text{arccot}}\left( { - \mu } \right)/{\text{π }} 时具有最佳的能量聚焦特性, 第m 个阵元信号直达波FRFT的峰值为{S}_{m,T}\left({p}_{0},{u}_{m,T}\right)=\sqrt{1-\text{j}\cot{\alpha }_{0}}{\rm e}^{{\rm{j}}\pi \left(-2{f}_{0}{\tau }_{m,T} + \mu {\tau }_{m,T}^{2}\right)}{\rm e}^{{\rm{j}}\pi {\mu }^{2}\cot{\alpha }_{0}}T\text{, } (12) 其中,
{\alpha _0} = {p_0}\pi /2 , 此时{u_{m,T}} 与\left( {{f_0},\mu } \right) 之间的关系为{{f_0} - \mu {\tau _{m,T}} = {u_{m,T}}\csc{\alpha _0}.} (13) 以首阵元为参考点, 由式(13)可得
{{u_{m,T}} = {u_{1,T}} + {\tau _{m,T}}\cos{\alpha _0}.} (14) {S}_{m,T}\left({p}_{0},{u}_{m,T}\right)={b}_{m,T}{S}_{1,T}\left({p}_{0},{u}_{1,T}\right)\text{, } (15) 其中
\begin{split} {b_{m,T}} =& {\text{e}}^{{\rm{j}}\pi ( { - 2{u_{1,T}}\csc{\alpha _0}{\tau _{m,T}} - \cot{\alpha _0}{{( {{\tau _{m,T}}} )}^2} + 2{\tau _{m,T}}{u_{1,T}}\cos{\alpha _0}\cot{\alpha _0} + \cos ^2 {\alpha _0}\cot{\alpha _0}{{( {{\tau _{m,T}}} )}^2}} )} = \\& {\text{e}}^{{\rm{j}}\pi ( { - 2{\tau _{m,T}}{u_{1,T}}\sin{\alpha _0}} )}{\text{e}}^{ - {\rm{j}}\pi {{( {{\tau _{m,T}}} )}^2}\sin{\alpha _0}\cos{\alpha _0}}. \\[-12pt] \end{split} (16) 式(14)和式(15)反映了不同阵元的直达波信号在FRFT域中出现峰值的位置和幅度的变化情况。式(16)给出了第
m 个阵元与首阵元之间峰值的相位差。信道衰落会导致阵元间信号的相关性减弱, 且后续阵元与首阵元之间峰值的相位差具有周期性, 会导致两阵元间的声程差计算产生模糊, 基于上述考虑, 在相位差计算中将当前阵元的前一阵元作为参考阵元, 由式(15)可得第
m 个阵元与第m + 1 个阵元之间峰值幅度的关系为{S_{m + 1,T}}\left( {{p_0},{u_{m + 1,T}}} \right) = {b_{m,m + 1}}{S_{m,T}} \left( {{p_0},{u_{m,T}}} \right), (17) 其中, 相位差为
{b}_{m,m + 1}={\rm e}^{{\rm{j}}\pi \left(-2\Delta {\tau }_{m,m + 1}{u}_{m,T}\sin{\alpha }_{0}\right)}{\rm e}^{-{\rm{j}}\pi {\left(\Delta {\tau }_{m,m + 1}\right)}^{2}\sin{\alpha }_{0}\cos{\alpha }_{0}}\text{, } (18) 其中,
\Delta {\tau _{m,m + 1}} = {\tau _{m + 1,T}} - {\tau _{m,T}} ,接下来可以通过该相位差实现阵形参数估计。\begin{split}& {\rm{Phase}}\left({b}_{m,m + 1}\right)=\\&\quad -2\pi \Delta {\tau }_{m,m + 1}{u}_{m,T}\sin{\alpha }_{0}-\pi {\left(\Delta {\tau }_{m,m + 1}\right)}^{2}\sin{\alpha }_{0}\cos{\alpha }_{0}\text{, } \end{split} (19) 其中,
{\rm{Phase}}\left( \cdot \right) 为求相位的计算, 令{\varPhi}_{1}=\pi \sin{\alpha }_{0}\cos{\alpha }_{0} ,{\varPhi}_{2}=2\pi {u}_{\text{m},\text{T}}\sin{\alpha }_{0} , 则第m 个阵元与第m + 1 个阵元间的声程差可表示为\Delta {R}_{m + 1,m}^{T}=c\frac{-{\varPhi}_{2}\pm \sqrt{{\varPhi}_{2}{}^{2}-4{\varphi}_{1}{\rm{Phase}}\left({b}_{m,m + 1}\right)}}{2{\varPhi}_{1}}\text{, } (20) 其中,
c 为声波在水中的传播速度, 相邻阵元间的声程差应小于相邻阵元间距d , 即{{\Delta }}R_{m + 1,m}^T \leqslant d , 根据此关系可很容易地从式(20)中选出真实的声程差。将{{\Delta }}R_{m + 1,m}^T 代入式(3), 可得第m 个阵元航向角为{\beta }_{m}={\theta }_{T}-\mathrm{arccos}\left(\frac{\Delta{R}_{m + 1,m}^{T}}{d}\right)\text{, } (21) 其中,
{\theta _T} 为直达波的入射角度。2.4 阵形解模糊方法
2.3节给出了阵形参数估计方法, 利用式(21)可实现对柔性水平阵各阵元航向角的估计, 但需要注意的是, 当
\left| {{{\Delta }}R_{m + 1,m}^T} \right| \ne d 时,{\beta _m} 存在两个关于{\theta _T} 对称的解, 其中一个为真实航向角, 另一个为模糊航向角。1.1节提出拖曳船机动过程中, 阵列一般会保持平滑的形状, 因此同一校准周期内各相邻阵元的航向角的关系应为连续变化, 本文根据该性质对各阵元估计航向角进行分组。此时由于模糊问题, 第
m 个阵元航向角为\left[ {{\beta _{m,1}},{\beta _{m,2}}} \right] , 第m + 1 个阵元航向角为\left[ {{\beta _{m + 1,1}},{\beta _{m + 1,2}}} \right] , 以{\;\beta _{m,1}} 为例, 分别计算其与\left[ {{\beta _{m + 1,1}},{\beta _{m + 1,2}}} \right] 之间差值的绝对值, 较小绝对值所对应的m + 1 阵元航向角与{\;\beta _{m,1}} 为一组航向角。由首阵元逐个递推, 从而实现全部航向角的分组, 并依据1.1节中提出的柔性水平阵模型得到估计出的两组阵形, 其中一组与柔性水平阵的真实阵形接近, 另一组为模糊阵形, 如图8所示。针对阵形模糊问题, 本节提出一种利用拖曳船辐射噪声对应的MUSIC空间谱幅度差异解阵形模糊的方法, 下面将对该方法进行详细描述: 拖曳船辐射噪声为宽带信号在拖曳过程中始终存在, 首先在当前阵形校准周期内从时域上挑选出不存在直达波及目标回波干扰的拖曳船辐射噪声, 将其划分为多个窄带, 由式(6)可得, 第
m 个阵元接收的拖曳船辐射噪声分频带后的信号为{Y_m}\left( f \right) , 阵列输出为{\boldsymbol{X}}\left( f \right) :{{\boldsymbol{X}}\left( f \right) = {{\left[ {{Y_1}\left( f \right), \cdots ,{Y_m}\left( f \right), \cdots ,{Y_M}\left( f \right)} \right]}^{\text{T}}}.} (22) 信号的协方差矩阵为
{{\boldsymbol{R}}_x}\left( f \right) = {\rm E}\left[ {{\boldsymbol{X}}\left( f \right){{\boldsymbol{X}}^{\rm H}}\left( f \right)} \right] , 对{{\boldsymbol{R}}_x}\left( f \right) 进行特征分解, 选取小特征值对应的特征矢量张成的子空间为噪声子空间{{\boldsymbol{U}}_N}\left( f \right) 。由于噪声子空间与真实阵形的导向矢量张成的空间相互正交, 与模糊阵形生成的导向矢量不满足正交性, 两阵形得到的空间谱幅度存在差异, 因此可对拖曳船辐射源所在区域\left( {x,y} \right) 内进行空间谱扫描, 式(23)为去模糊算法的空间谱扫描结果:J\left({\boldsymbol{a}}\right)=\underset{\text{x},\text{y}}{\text{max}}\left(\displaystyle \sum _{i=1}^{I}\frac{1}{{{\boldsymbol{a}}}^{\rm H}\left(x,y,{f}_{i}\right){{\boldsymbol{U}}}_{N}\left({f}_{i}\right){{\boldsymbol{U}}}_{N}^{\rm H}\left({f}_{i}\right){\boldsymbol{a}}\left(x,y,{f}_{i}\right)}\right)\text{, } (23) 其中,
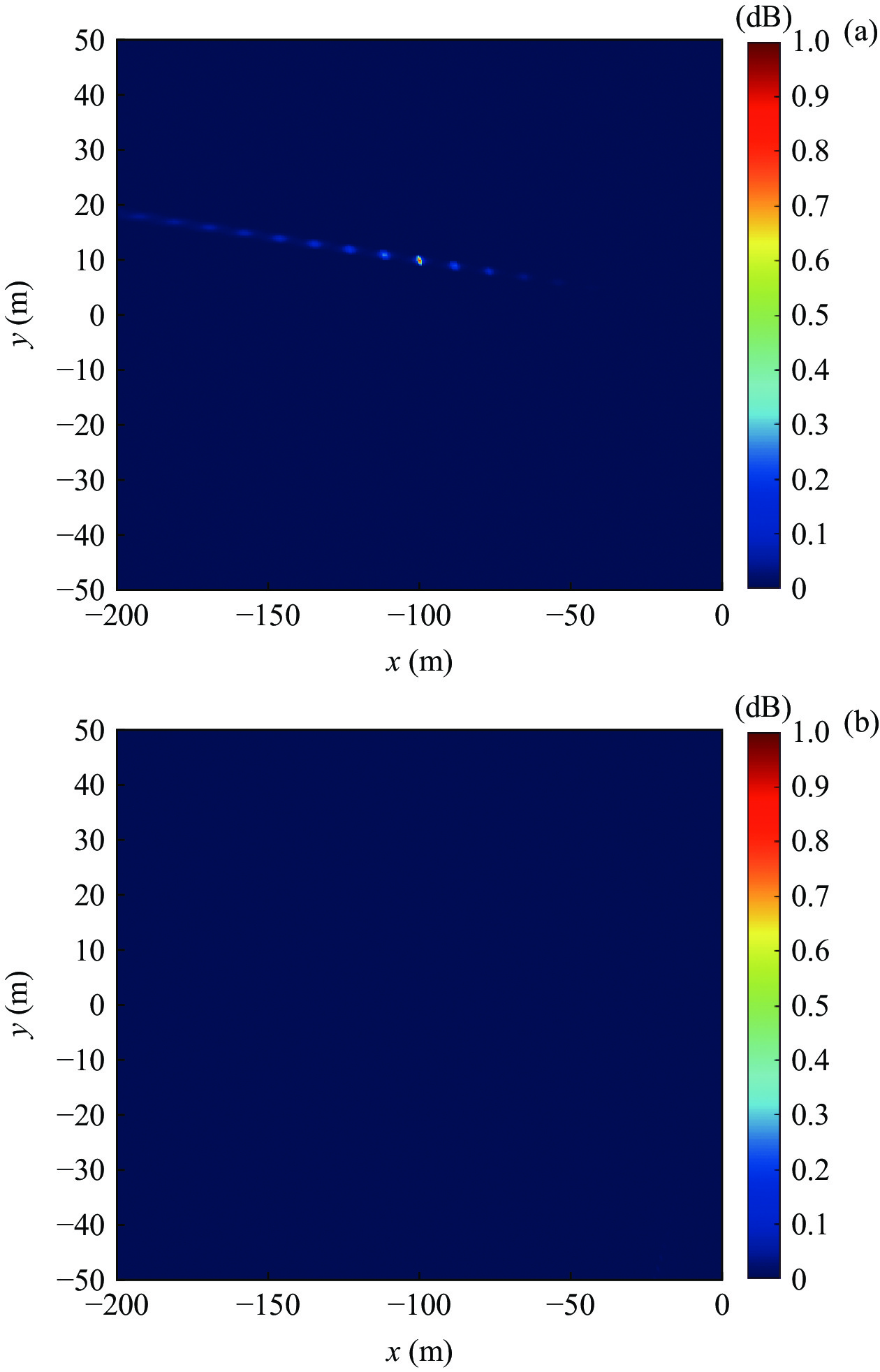
{f_i}\left( {i = 1,2, \cdots ,I} \right) 为各窄带的中心频率,{\boldsymbol{a}} 为利用两估计阵形得到的近场阵列流形矩阵。无噪声的情况下, 当J\left( {\boldsymbol{a}} \right) 的分母为0时, 此时对应生成该阵列流形矩阵{\boldsymbol{a}} 的阵形即为真实阵形。利用该性质,J\left( {\boldsymbol{a}} \right) 最大值所对应的阵形与真实阵形更加接近, 从而实现阵形解模糊。需要注意的是当拖曳船辐射噪声与直达波入射角度一致时, 两估计阵形计算得到的辐射噪声的空间谱强度相同, 无法实现阵形的模糊辨识, 此时可考虑利用阵形的时间连续性进行估计阵形辨识, 阵形随时间的变化连续且缓慢, 当某一校准周期拖曳船辐射噪声入射角度与直达波入射角度一致时, 可利用前一校准周期阵形辨识后的估计阵形, 计算其与当前校准周期估计阵形的均方根差值, 较小差值所对应的阵形即为当前周期的真实阵形。通过仿真验证本节提出阵形解模糊方法的有效性, 仿真参数为: 接收阵为80 元等间距的柔性水平阵, 阵元间距为0.25 m, 拖曳船噪声源为宽带近场噪声源, 信噪比为0 dB, 声源坐标为
\left( { - 100{\text{ }}{\rm{m}},10{\text{ }}{\rm{m}}} \right) , 利用图8中两估计阵形分别计算拖曳船辐射噪声的近场宽带归一化MUSIC谱, 扫描范围为x\in \left(-200\text{ }{\rm{m}},0\text{ }{\rm{m}}\right), y\in \left(-50\text{ }{\rm{m}},50\text{ }{\rm{m}}\right) 的长方形区域, 扫描间隔为1 m, 如图9所示。可以看出, 估计阵形1相比估计阵形2得到的空间谱存在明显亮点, 验证了阵形解模糊方法的有效性。3. 数值仿真验证
本节将通过计算机仿真详细分析本文提出的算法对直达波提取以及阵形参数校准的性能, 如无特殊说明, 本节实验均采用第2节所述算法。
3.1 方法有效性验证
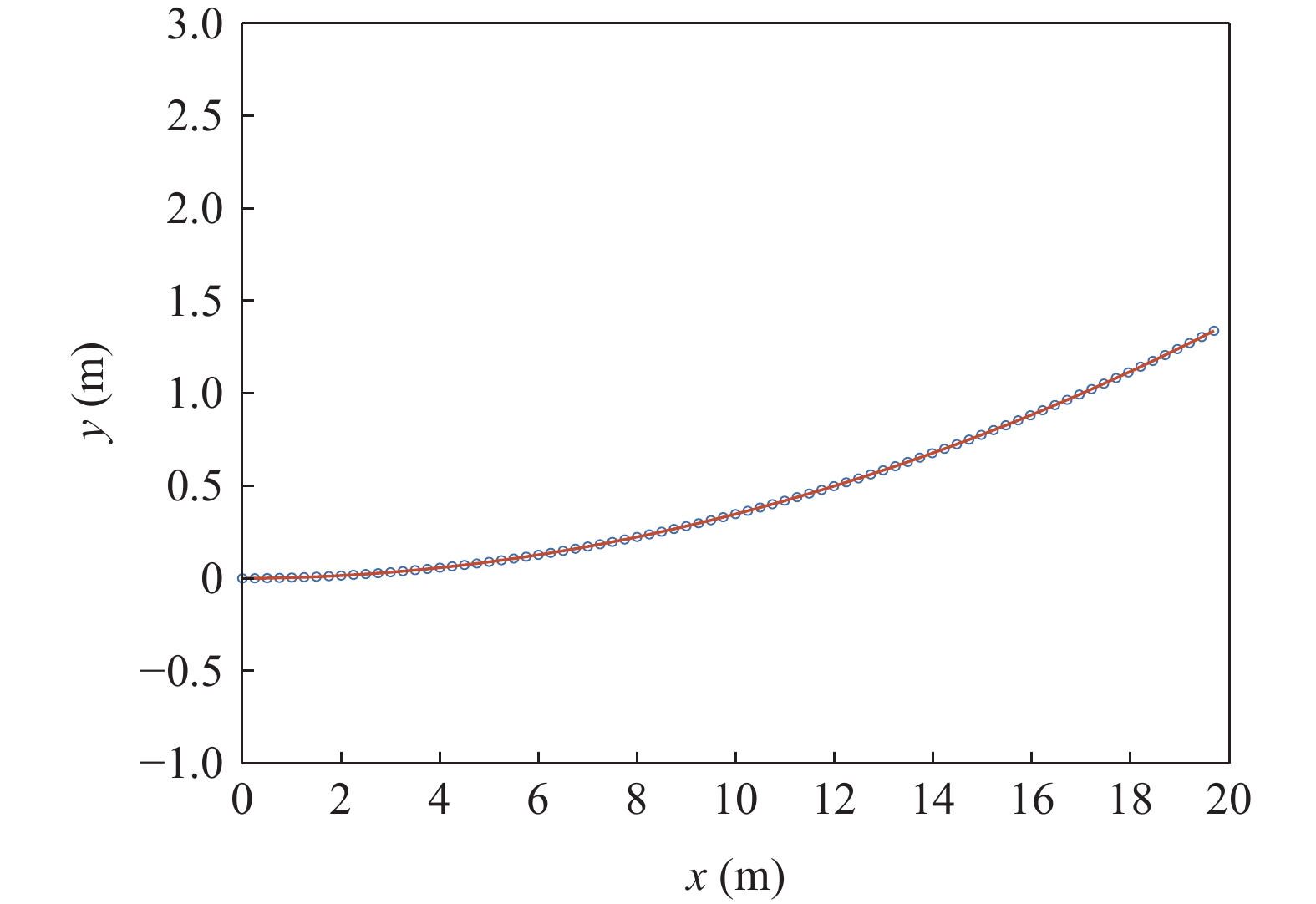
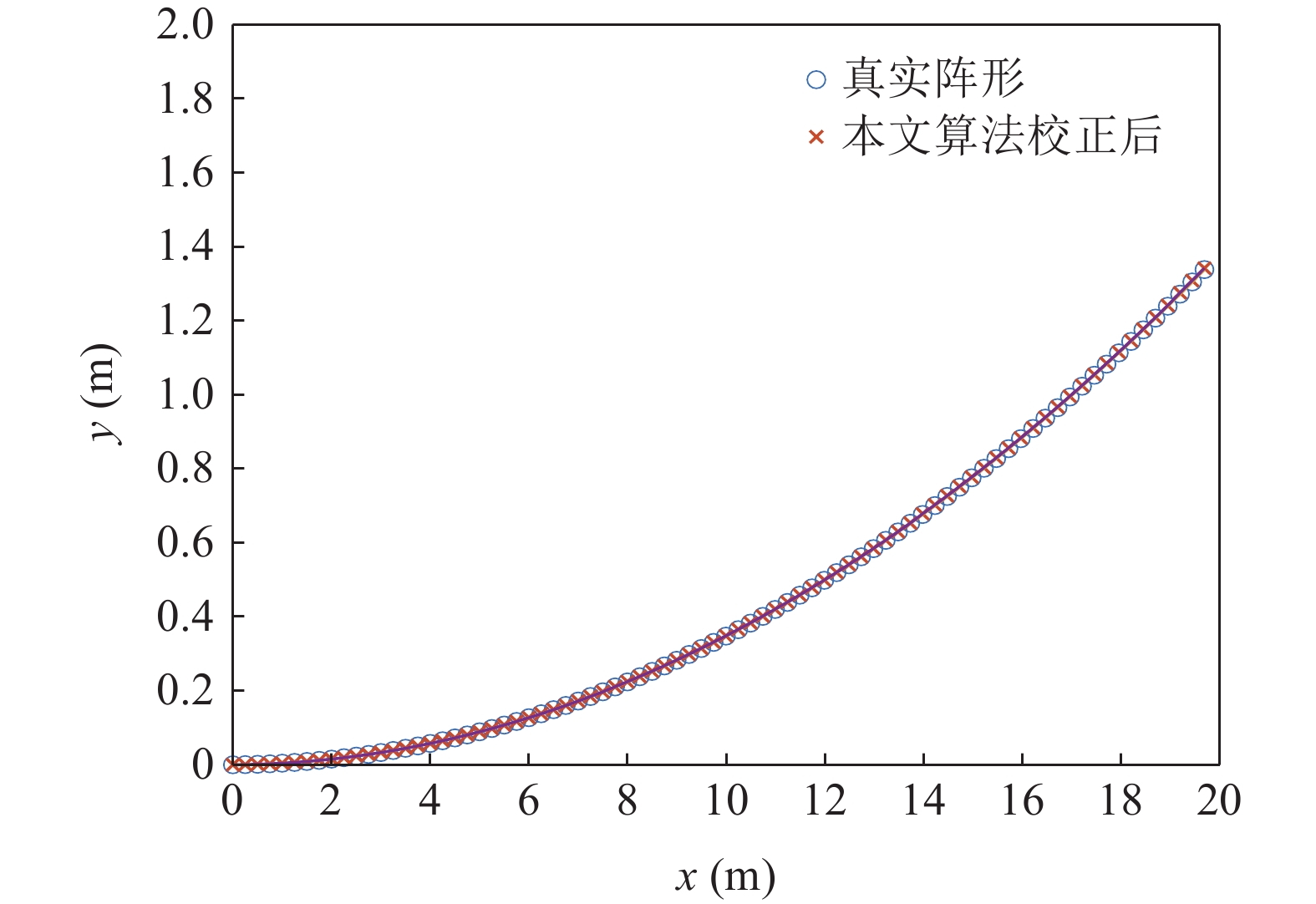
验证直达波提取后本文提出算法进行阵形估计的效果。仿真中, 接收阵为80 元等间距的柔性水平阵, 阵元间距为0.25 m, 发生畸变时的柔性水平阵模型如图10所示。
由于常规波束形成中需选取参考声速, 声速剖面存在变化对目标测向精度的影响不可忽视[23], 因此仿真背景考虑在等声速平面下, 参考声速为1500 m/s。2.2节已验证了FRFT在信道仿真背景下信号分离能力, 因此本节仿真的直达波和目标回波信号仅考虑不经海面海底反射的首达信号。发射信号为脉宽0.4 s、带宽500 Hz、中心频率3000 Hz的LFM信号。直达波信噪比为30 dB, 将目标回波视作干扰, 直达波与目标回波的信干比为20 dB, 入射角度分别为30 °和120 °。参考阵元中直达波与目标回波信号的时频图如图11所示, 此时直达波与目标回波信号时域部分重叠。
直达波提取后利用本文所提算法估计阵形参数, 如图12所示。比较阵形参数估计前后目标回波方位的估计情况, 其中目标回波方位谱的计算过程如下: 常规波束形成后进行拷贝相关, 得到的方位历程图在目标回波结束时刻的时间切片即为目标回波方位谱图, 如图13所示。
从图12可以看出本文算法估计得到的阵形估计结果与真实阵形接近, 验证了本文提出算法对于阵形估计的有效性。由图13可以看出经过阵形参数估计后, 方位估计精度得到明显的改善, 方位谱估计结果与利用真实阵列阵形信息得到的估计结果更加接近, 验证了阵形估计结果的准确性。
3.2 阵形参数估计精度分析
阵形参数估计精度可由阵元估计位置与真实位置偏差的均方根误差(RMSE)体现, RMSE计算公式为
{\rm{RMSE}}={\left(\frac{1}{M\times N}\displaystyle \sum _{l=1}^{N}\displaystyle \sum _{m=1}^{M}\left({\left({\widehat{x}}_{m}^{l} - {x}_{m}\right)}^{2} + {\left({\widehat{y}}_{m}^{l} - {y}_{m}\right)}^{2}\right)\right)}^{1/2}\text{, } (24) 其中,
N 为蒙特卡洛次数,\left( {{x_m},{y_m}} \right) 为第m 个阵元的真实坐标,( {\widehat x_m^l,\widehat y_m^l} ) 为第l 次独立实验中第m 个阵元的估计坐标。阵形参数估计的均方根误差常与发射信号中心频率对应的波长进行比较, 以验证参数估计的准确性。在下面的分析中均将RMSE的坐标刻度转变为波长。为分析不同均方根误差下, 阵列阵增益以及波束图主瓣指向角度偏差的变化情况, 对各阵元位置分别加入
\pm \Delta \lambda 的均匀随机误差得到\left( {x_m',y_m'} \right) , 通过调整\Delta \lambda 的范围获得不同的均方根误差, 每种范围内的蒙特卡洛次数为2000, 此时均方根误差{\text{RMSE}} 按照式(25)进行计算, 每种范围内的阵增益及波束图主瓣指向角度偏差的变化情况分别按照式(26)和式(27)计算:{\rm{RMSE}}={\left(\frac{1}{M\times 2000}\displaystyle \sum _{l=1}^{2000}\displaystyle \sum _{m=1}^{M}\left({\left({x}_{m}^{l}-{x}_{m}\right)}^{2} + {\left({y}_{m}^{l} - {y}_{m}\right)}^{2}\right)\right)}^{1/2}\text{, } (25) {\rm AG}{{'}}=\frac{1}{2000}\displaystyle \sum _{l=1}^{2000}10\text{lg}\left(\frac{{\left|{W}^{H}{{\boldsymbol{A}}}_{l}\left({\theta }_{0}\right)\right|}^{2}}{{W}^{H}{{\boldsymbol{R}}}_{n}W/{p}_{n}}\right)\text{, } (26) {\theta ' = \frac{1}{{2000}}\mathop \sum \limits_{l = 1}^{2000} (| {{\text{max}}( {| {{W^H}{{\boldsymbol{A}}_l}( \Theta )} |}) - {\theta _0}} |).} (27) 式(25)中
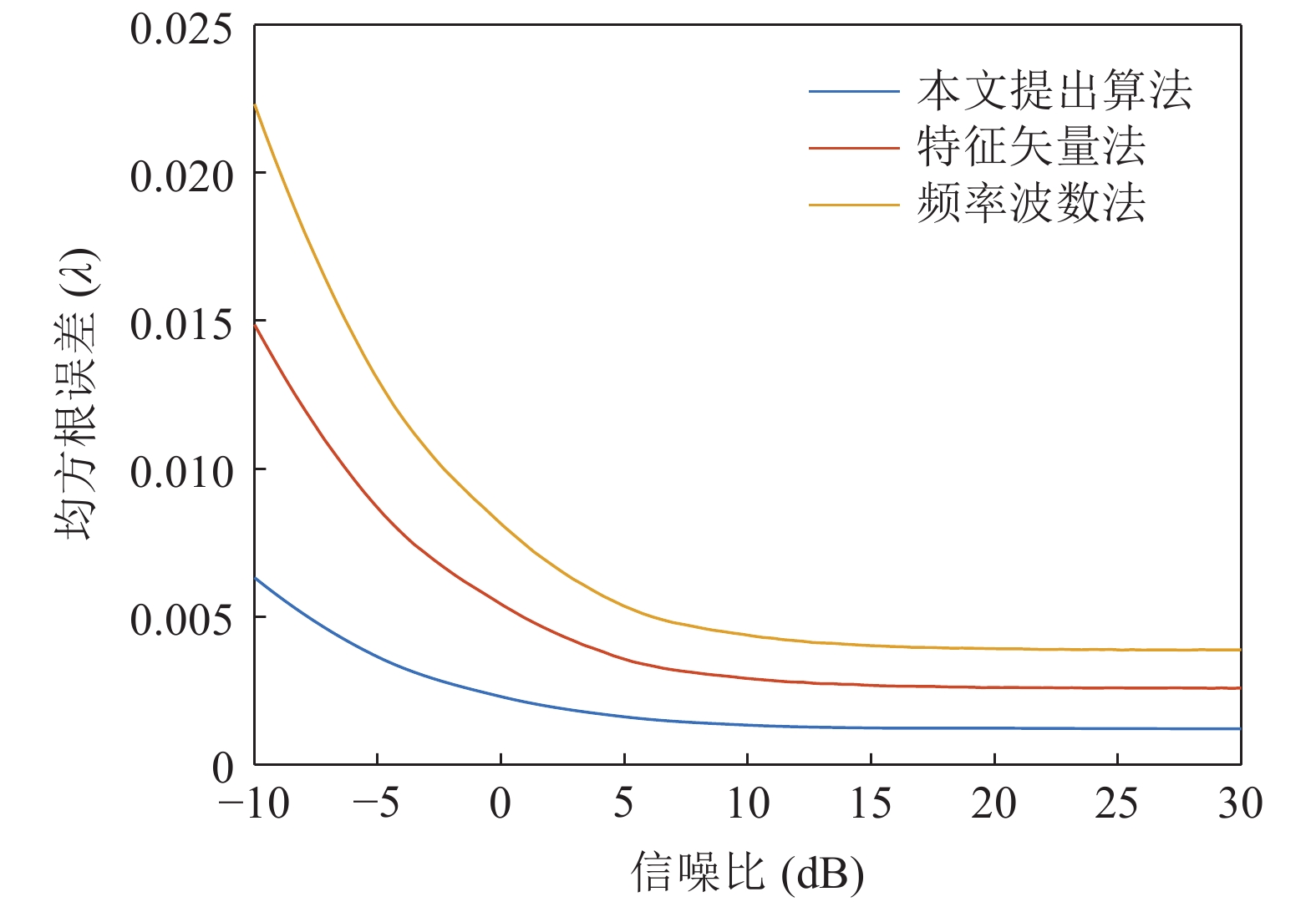
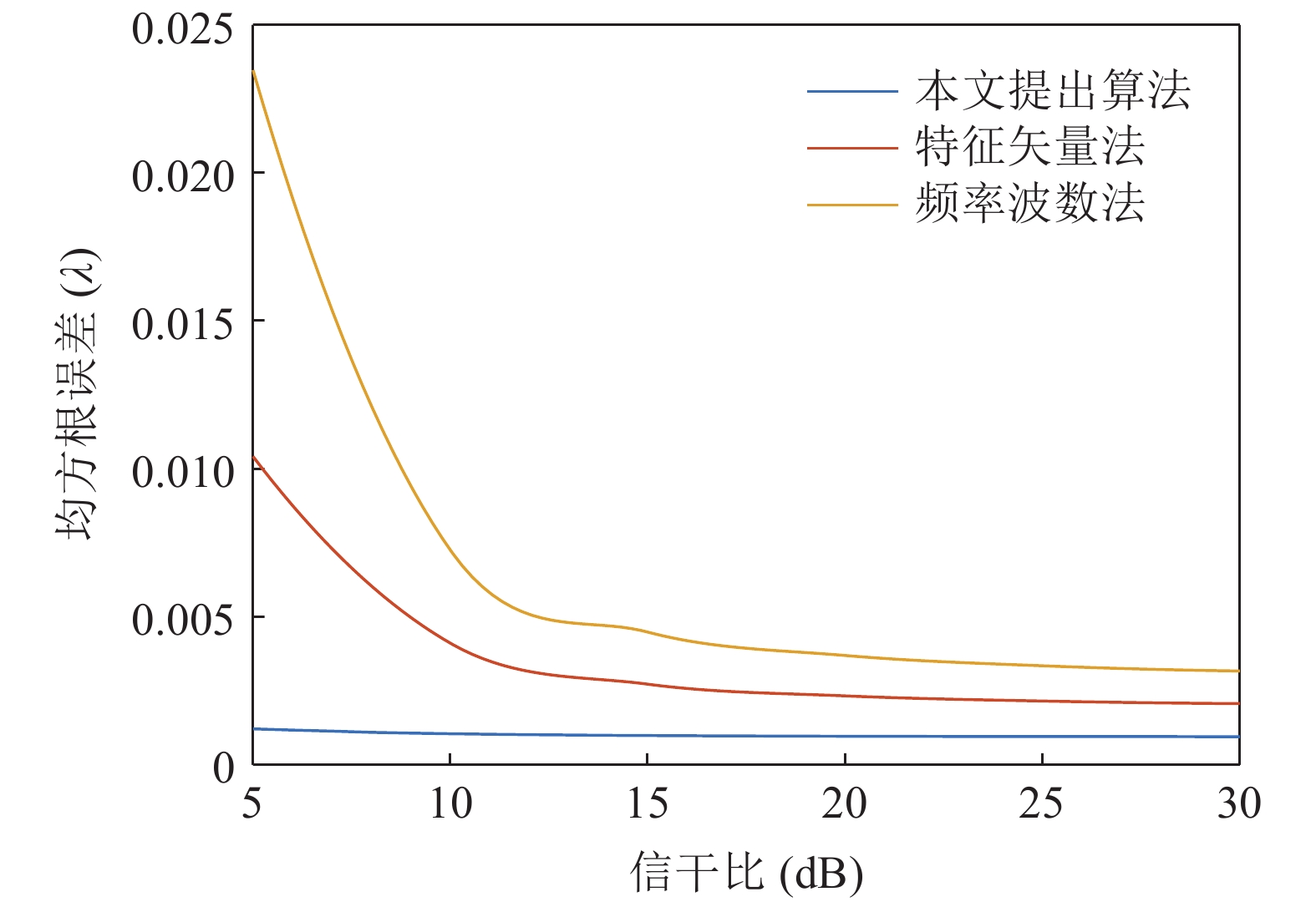
\left( {x_m^l,y_m^l} \right) 为第l 次独立实验中第m 个阵元的偏移坐标。式(26)中{A_l}\left( {{\theta _0}} \right) 表示第l 次独立实验中偏移阵列对应的入射信号方向矢量, 其中{\theta _0} = 120^\circ ,{{\boldsymbol{R}}_n} 表示噪声协方差矩阵, 噪声为空间白噪声时,{{\boldsymbol{R}}_n} = {p_n}{\boldsymbol{I}} ,{p_n} 为噪声平均功率。在波束设计中, 一般对加权向量进行归一化, 即让\left| {{W^H}{\boldsymbol{A}}\left( {{\theta _0}} \right)} \right| = 1 , 其中{\boldsymbol{A}}\left( {{\theta _0}} \right) 为阵列无偏移时入射信号方向矢量。式(27)中{{\boldsymbol{A}}_l}\left( \varTheta \right) 表示第l 次独立实验中偏移阵列对应的阵列流形矩阵,{\text{max}}\left( \cdot \right) 表示波束图最大幅度所对应的角度。阵列阵形存在不同均方根误差时对应的阵增益以及波束图主瓣指向角度偏差的变化情况如图14所示。仿真条件同3.1节, 分析直达波的信噪比以及信干比对RMSE的影响情况。固定信干比为20 dB, 每种信噪比下蒙特卡洛实验次数为2000 , 3种算法估计结果的RMSE随信噪比的变化情况如图15所示。固定直达波信噪比为
30{\text{ }}{\rm{dB}} , 每种信干比下蒙特卡洛实验次数为2000, 三种算法估计结果的RMSE随信干比的变化情况如图16所示。从图15可以看出, RMSE随着信噪比的提高逐渐降低, 信噪比为−10 dB时, 本文提出算法对应的RMSE仍然可以达到
0.006\lambda , 相比于特征矢量法和频率波数法阵形估计精度有所提高。由图16同样可以看出信干比也是影响RMSE的因素之一, 随着信干比的降低, 本文算法的RMSE并未明显增加, 这也验证了本文提出的直达波提取算法的有效性, 相比于特征矢量法和频率波数法具有更好的抗干扰特性。3.3 入射角度误差分析
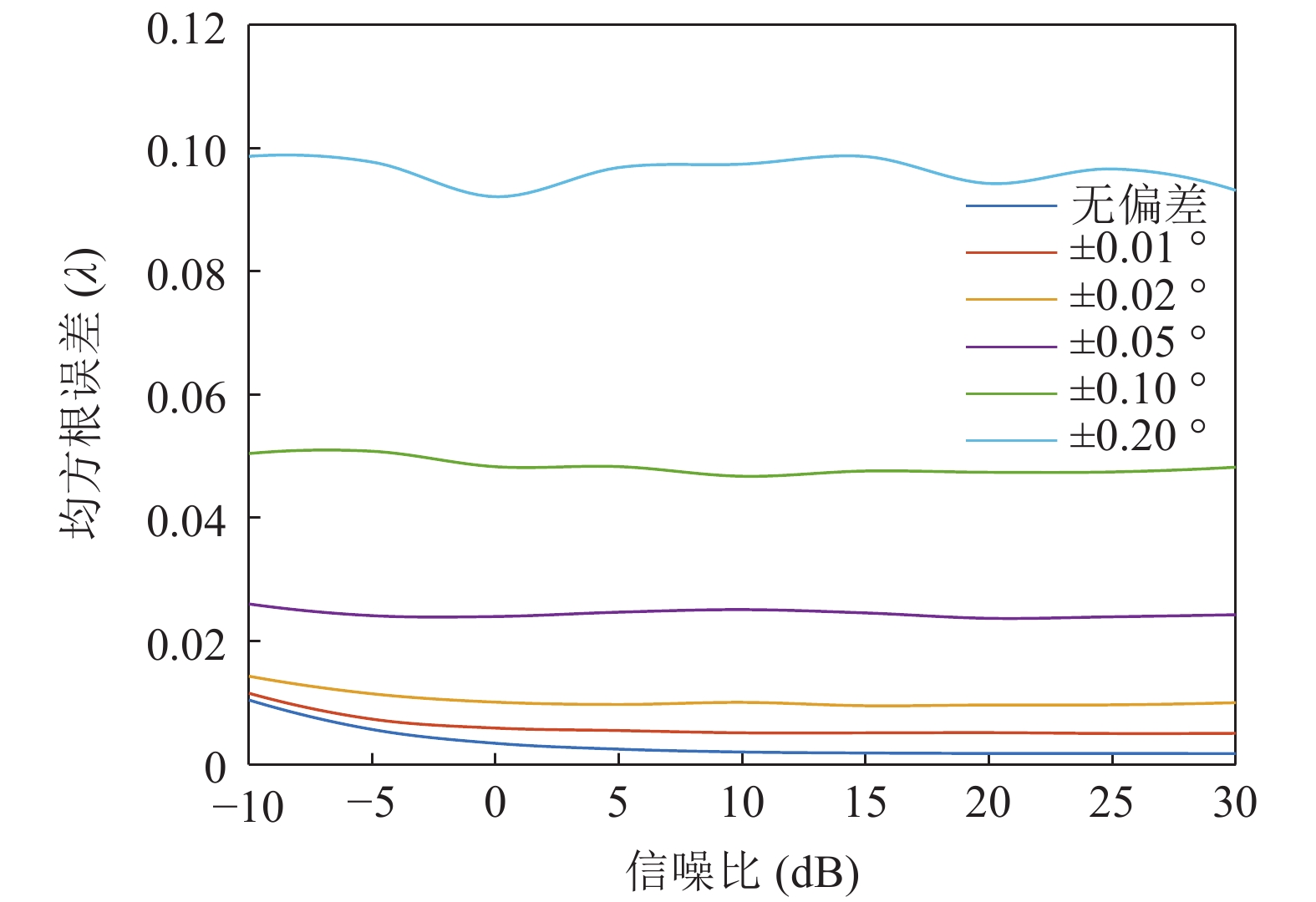
直达波入射角度可由发射基地与接收基地之间的先验位置信息得到, 下面分析由于接收和发射基地的GPS、拖曳船航向等测量误差所引起的入射角度计算误差, 即算法稳健性。仿真条件同3.1节, 对直达波入射角度分别加入
\pm 0.01^\circ ,\pm 0.02^\circ ,\pm 0.05^\circ ,\pm 0.10^\circ ,\pm 0.20^\circ 的均匀随机误差, 每种信噪比下的蒙特卡洛次数为2000, 不同角度误差下的RMSE曲线如图17所示。从图17可以看出, 在入射角度的先验信息无误差时, 阵元位置估计RMSE可达到
{10^{ - 3}}\lambda 数量级, 随着入射角度误差增大, RMSE也随之增大。相比于信噪比对RMSE的影响, 可以看出入射角度误差对RMSE影响更大, 当角度误差在\pm 0.20{\text{ }}^\circ 以内时, RMSE仍然小于\lambda /10 , 说明该算法对于入射角度误差具有宽容性。3.4 多普勒影响分析
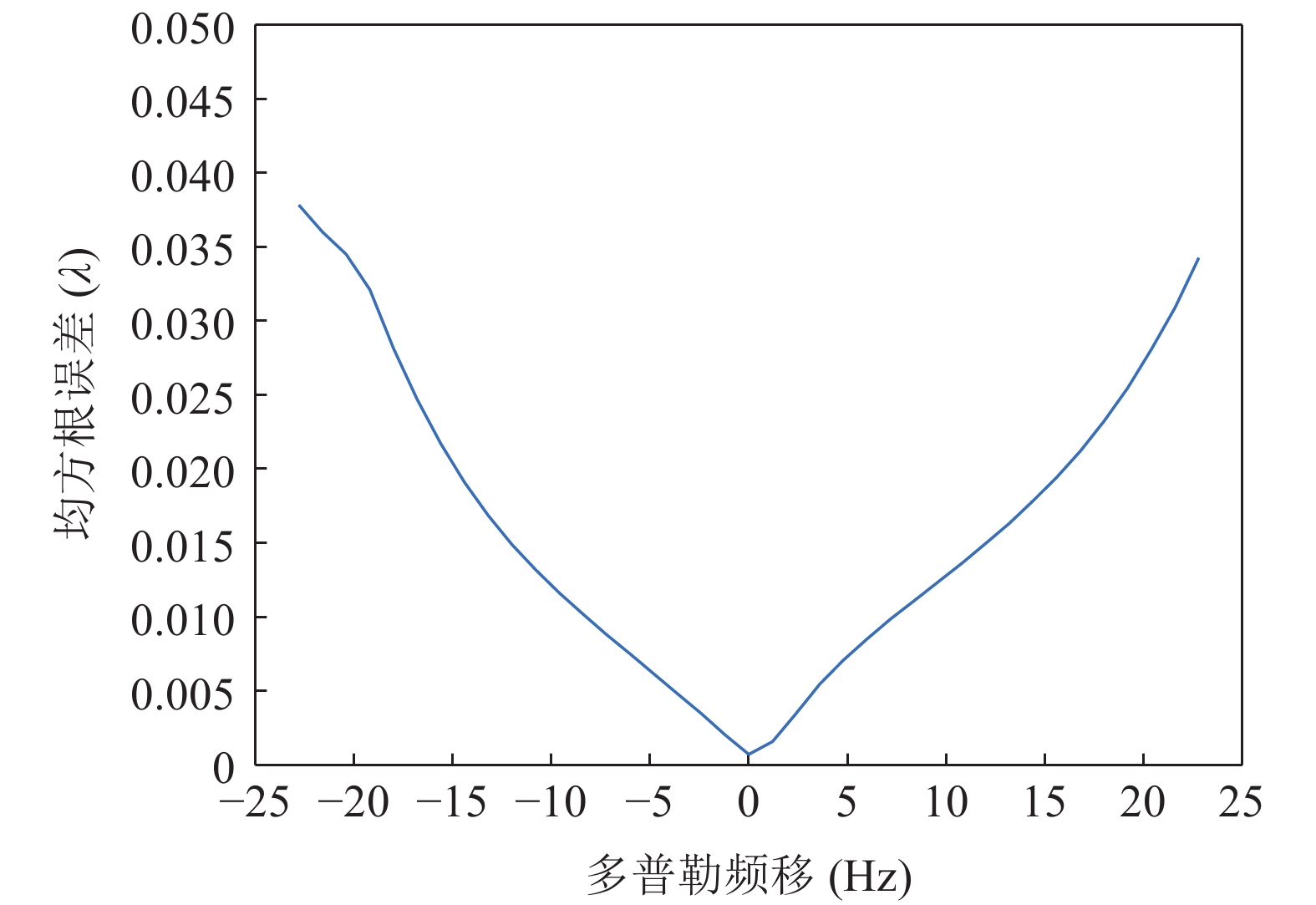
发射、接收基地的相对运动, 会导致接收的直达波信号最佳FRFT阶数偏离预成的FRFT阶数。仿真条件同3.1节, 发射基地与接收基地间存在多普勒频移时, 阵列参数估计的RMSE曲线如图18所示。
从图18可以看出, 当存在不同程度的多普勒频移时, 阵元估计位置的均方误差会发生改变, 随着多普勒频移的增大, RMSE逐渐增大。这是由于信号无法在预成的FRFT阶数下形成能量聚焦, 如图4所示, 从而导致了RMSE增大。但RMSE仍然可以达到
{10^{ - 2}}\lambda 级, 说明该方法对于多普勒频移具有良好的宽容性。4. 实验数据验证
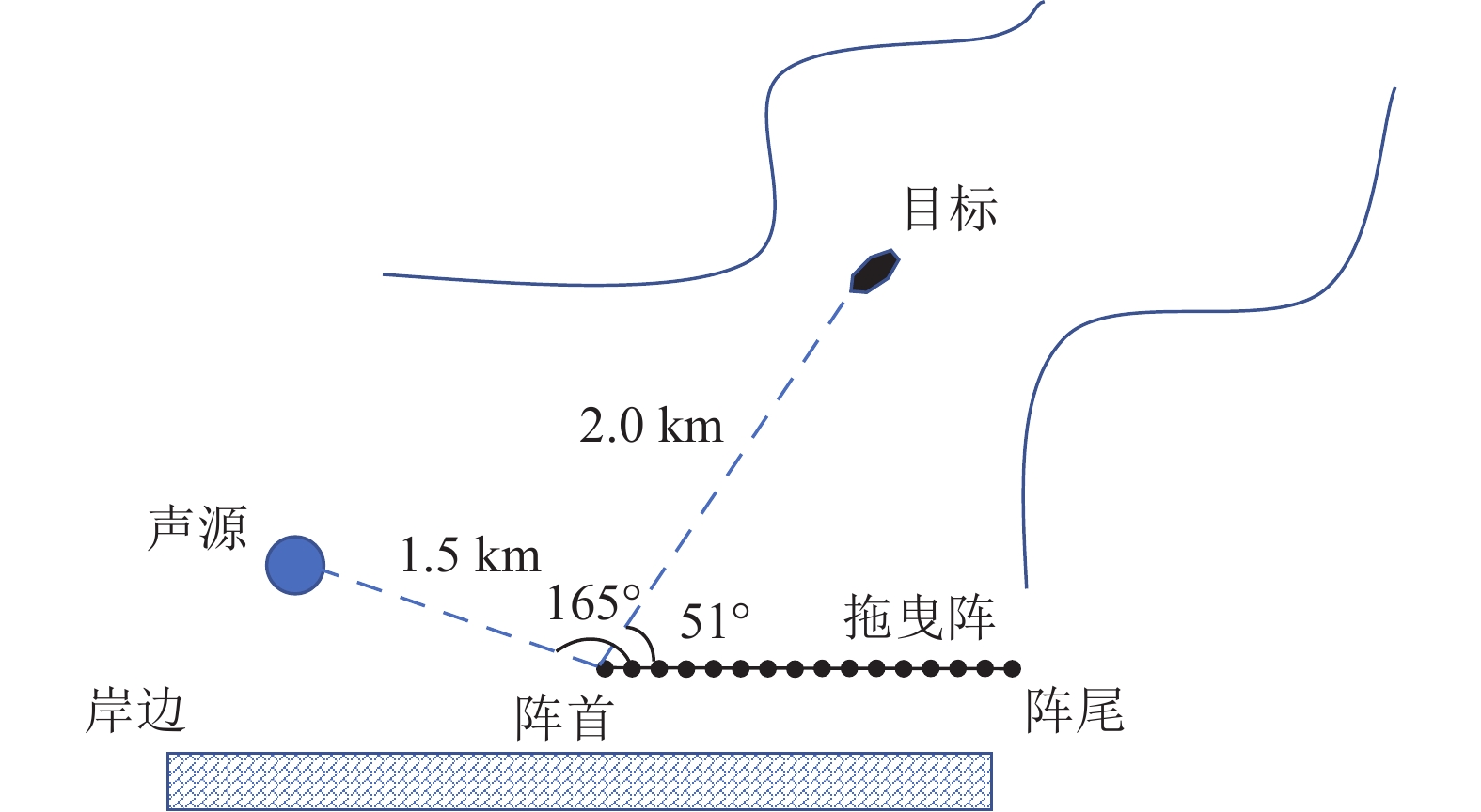
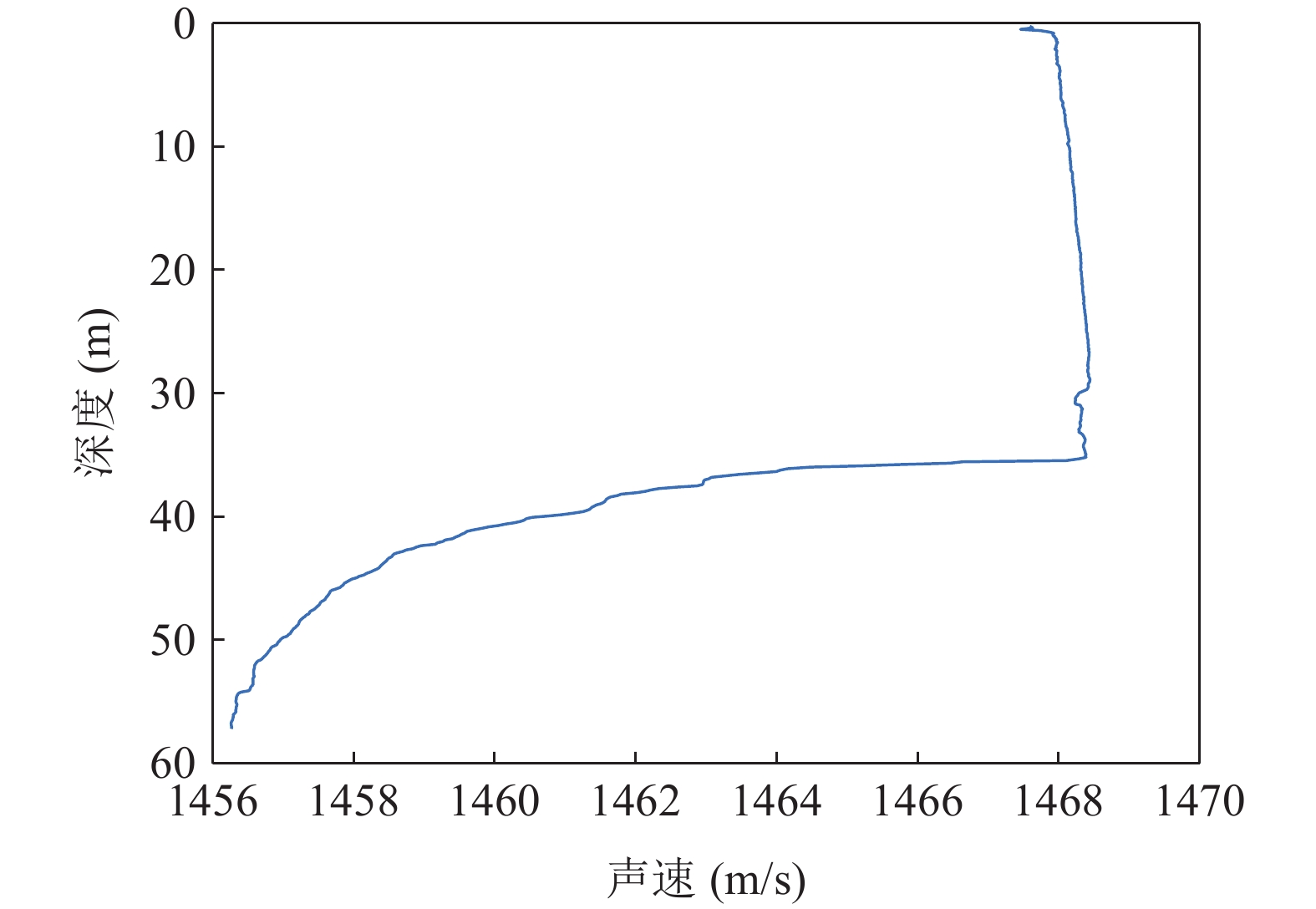
实验数据来自2021年1月在千岛湖开展的一次光纤柔性水平阵有源探测实验, 光纤柔性水平阵为80元等间距线阵, 阵元间距为信号中心频率的半波长, 实际阵列的阵元间距较短, 柔性水平阵阵形与图1展示的柔性水平阵模型匹配度较高。由于试验场地水深较浅, 两侧岸边距离较近, 不具备拖曳条件, 将柔性水平阵阵首与趸船连接, 在柔性水平阵各处捆绑浮球使其悬浮于水中, 只考虑由于试验场地中水流影响柔性阵产生的水平面内畸变。探测信号为LFM信号, 脉宽0.4 s, 归一化起止频率分别为0.1625, 0.1975, 其中归一化频率范围在
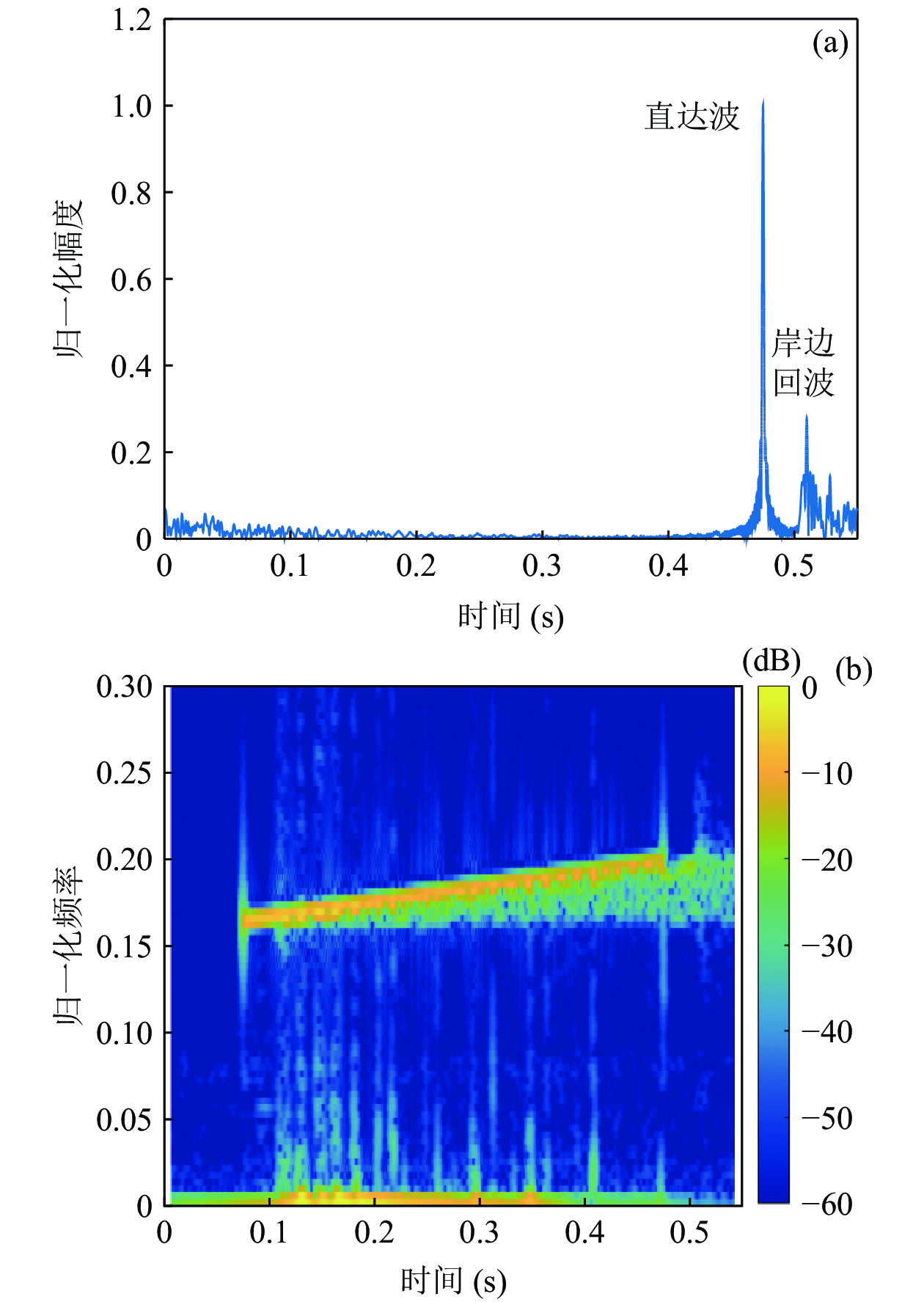
\left[ {0,1} \right] 之间, 以采样频率的一半作为频率归一化处理的分母。发射信号时声源、目标和接收阵的相对位置如图19所示, 其中声源深度10 m, 目标深度20 m, 接收阵深度5 m, 直达波及目标回波入射角度由阵首、阵尾、目标及声源的GPS位置得到, GPS定位精度受天气、物体遮挡等因素影响, 在宽阔湖面上并无物体遮挡, 且当日天气状况良好, 定位精度较高, 声速剖面如图20所示。首阵元接收信号的拷贝相关结果及短时傅里叶变换结果如图21所示, 由于声源位置靠近岸边, 接收信号的直达波中存在来自沿岸的回波干扰, 其中首阵元接收的直达波信噪比约为45 dB, 与岸边回波干扰的信干比约为10 dB, 阵尾阵元接收信号的信噪比约为42 dB, 信干比约为10 dB。目标位于直达波掩蔽区域以外, 因此目标回波时域上与直达波不重叠。
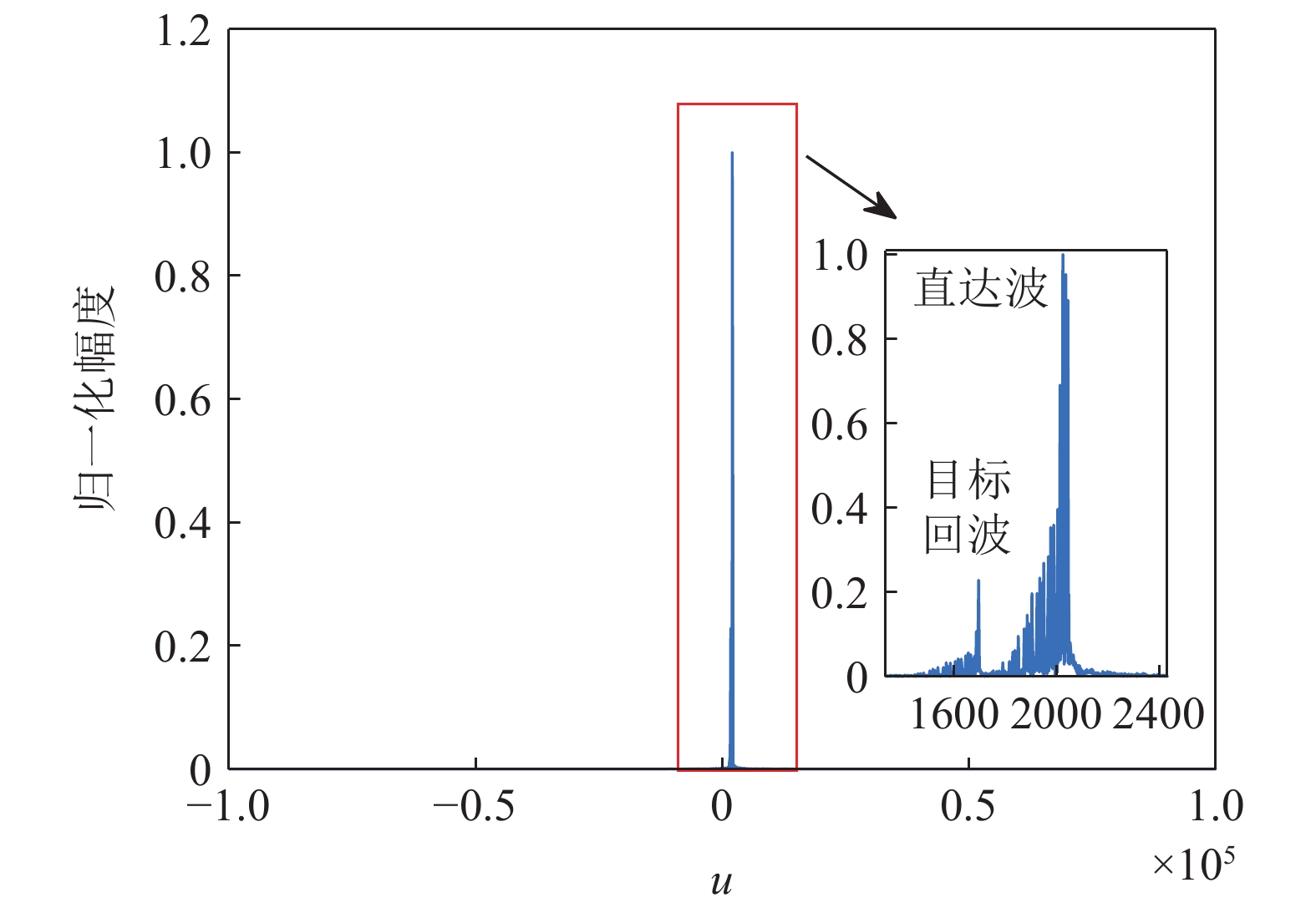
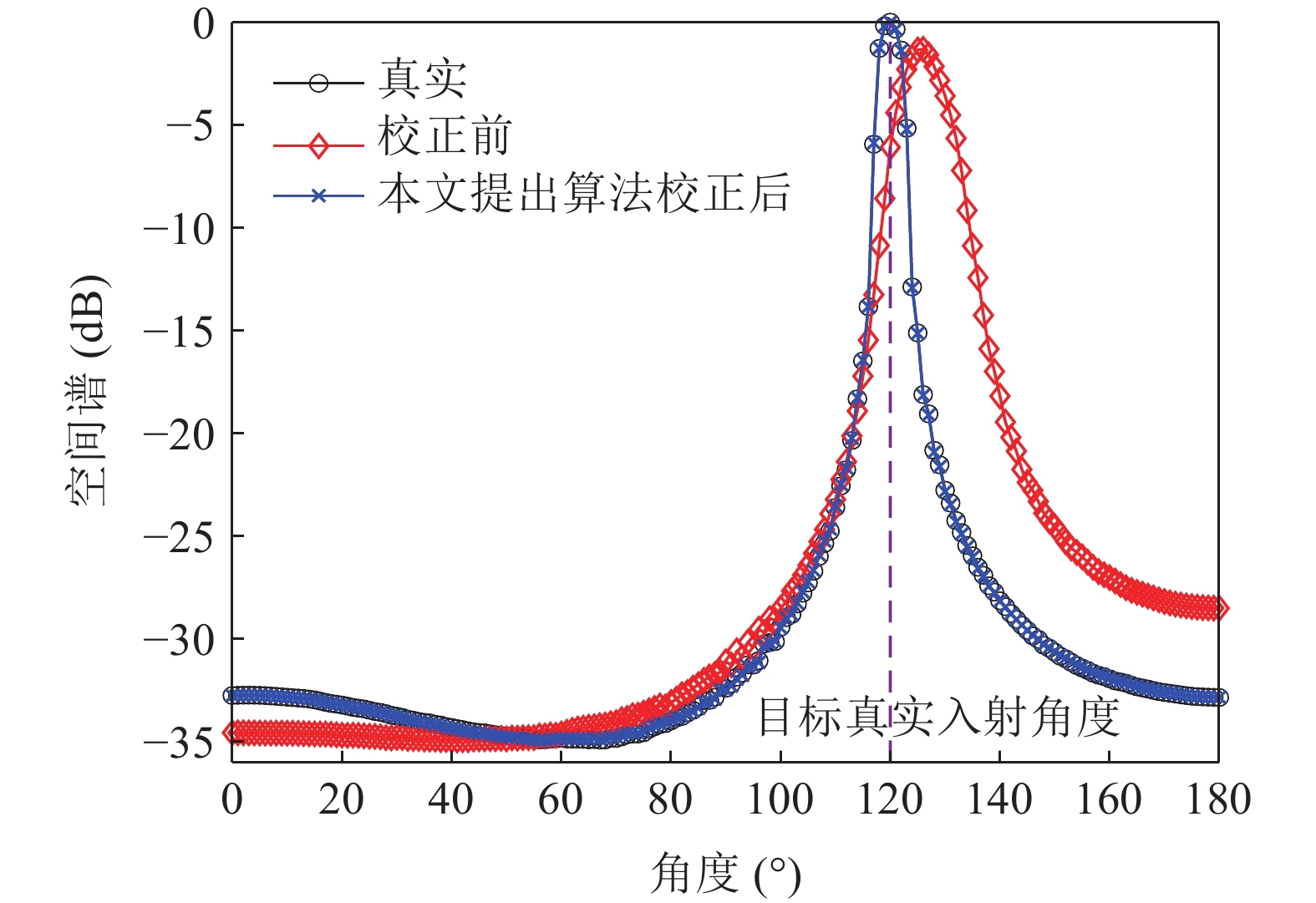
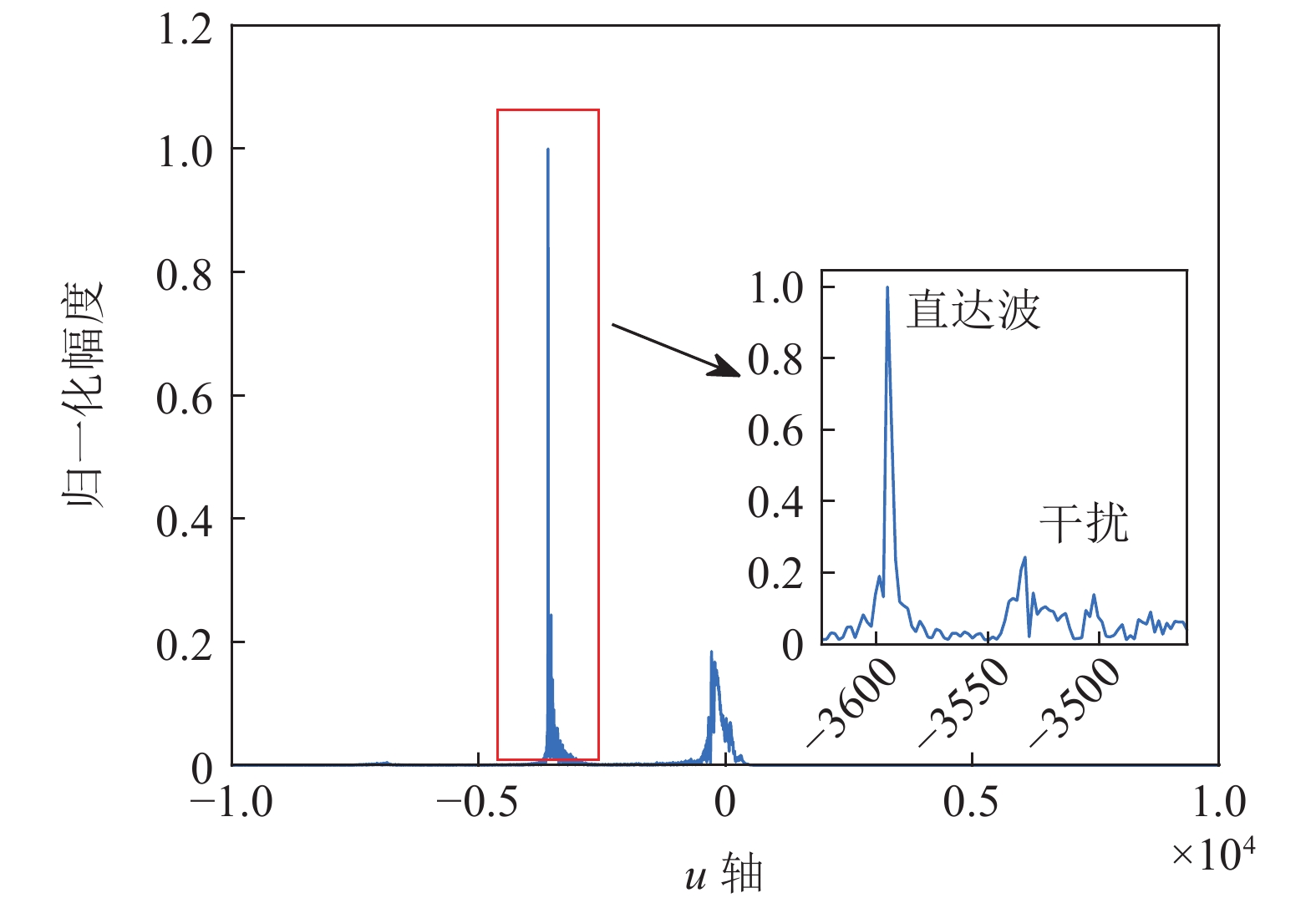
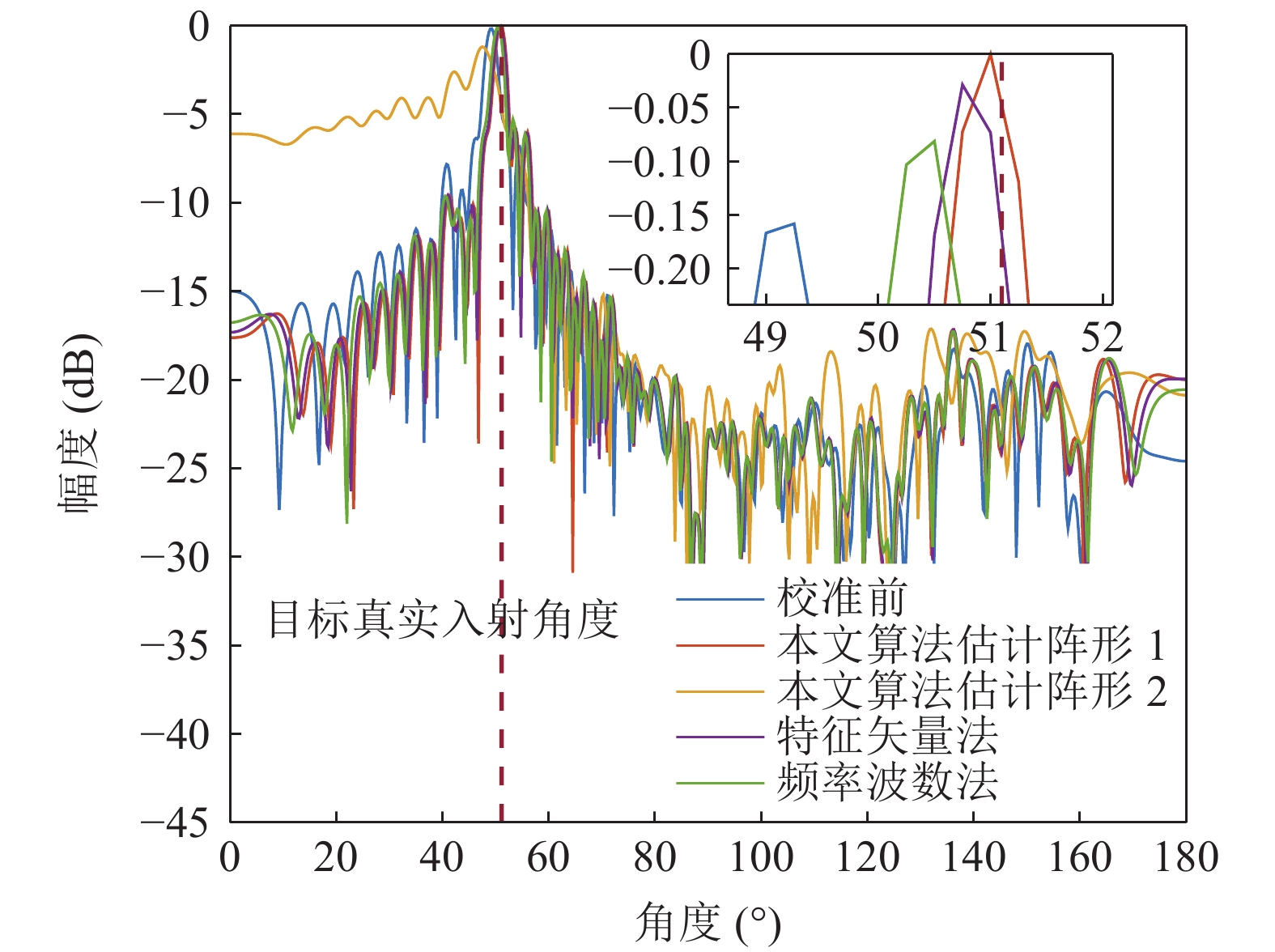
直达波在分数阶傅里叶变换后的结果如图22所示。利用默认阵形(校准前的标称阵形)、特征矢量法、频率波数法、本文提出算法估计阵形得到的目标回波方位谱图如图23所示, 其中黄色实线为模糊阵形条件下得到的目标回波方位谱估计,。
图22展示出分数阶傅里叶变换对于直达波良好的提取效果, 存在图21中所示干扰的情况下, 仍然可以在FRFT域实现直达波的能量聚集, 并与干扰分离, 提高后续利用直达波对应峰值进行柔性水平阵形估计的准确性。
图23中橘色实线及黄色实线分别为本文算法估计两阵形对应的目标回波方位谱, 可以看出阵形2得到的方位谱峰值对应角度大幅偏离目标回波真实入射角度, 且相比于阵形1幅度下降1.2 dB, 可轻易从两阵形中实现模糊阵形的辨识, 局部放大图展示了经过本文算法与校准前及其他算法校准阵形后测向的结果, 其中本文算法、特征矢量法、频率波数法得到的阵形, 以及校准前的阵形的测向偏差分别为0.10°, 0.35°, 0.60°, 1.85°, 本文提出算法与目标真实角度更加接近, 且方位谱峰值幅度更高, 验证了本文提出算法的有效性。
5. 结论
针对双基地有源模式下接收基地的柔性水平阵阵形参数估计的问题, 本文提出了一种利用直达波作为校准源对接收基地进行阵形参数估计的方法。对于可能出现的回波干扰, 利用FRFT进行直达波的提取, 并在信号提取的基础上, 实现了对阵形的参数估计, 并利用拖曳船辐射噪声的近场空间谱解决了阵形估计的模糊问题。该算法相比于传统参数估计方法, 抑制了信号干扰, 提高了阵形参数的估计精度, 且对噪声及干扰影响、入射角度误差、多普勒频移具有较强的宽容性, 实际数据处理结果验证了阵形参数估计方法的可行性。
-
[1] 李启虎. 水声信号处理领域新进展. 应用声学, 2012; 31(1): 2—9 DOI: 10.11684/j.issn.1000-310X.2012.01.002 [2] 王鲁军. 国外低频主动拖曳声呐发展现状和趋势. 水下无人系统学报, 2018; 26(3): 193—199 DOI: 10.11993/j.issn.2096-3920.2018.03.002 [3] 徐雅南. 高海况下拖曳阵阵形扰动及接收信号特性研究. 舰船电子工程, 2016; 36(4): 146—150 DOI: 10.3969/j.issn.1672-9730.2016.04.039 [4] Park H Y, Youn D H, Lee C, et al. Evaluation of the calibration method using iterative spline interpolation for array estimation. IEEE Oceans, Kobe, Japan, 2004: 593—597
[5] 焦君圣. 本艇机动时拖曳阵的阵形估计及左右舷分辨方法. 声学与电子工程, 2007(4): 16—19 [6] 罗薇, 张攀. 拖缆系统运动仿真. 武汉理工大学学报(交通科学与工程版), 2005; 29(5): 724—726 DOI: 10.3963/j.issn.2095-3844.2005.05.022 [7] Odom J L, Krolik J L. Passive towed array shape estimation using heading and acoustic data. IEEE J. Oceanic Eng., 2015; 40(2): 465—474 DOI: 10.1109/JOE.2014.2318531
[8] Park H Y, Kim K M, Kang H W, et al. A simplified subspace fitting method for estimating shape of a towed array. IEEE J. Oceanic Eng., 2008; 33(2): 215—223 DOI: 10.1109/JOE.2008.923556
[9] 梁国龙, 张柯, 安少军, 等. 声矢量阵阵元姿态误差自校正算法研究. 兵工学报, 2014; 35(8): 1236—1242 DOI: 10.3969/j.issn.1000-1093.2014.08.016 [10] Bucker H. Beamforming a towed array of unknown shape. J. Acoust. Soc. Am., 1978; 63(2): 1451—1454 DOI: 10.1121/1.381890
[11] 王燕, 邹男, 梁国龙. 强多途环境下水听器阵列位置近场有源校正方法. 物理学报, 2015; 64(2): 287—296 DOI: 10.7498/aps.64.024304 [12] 梁国龙, 邱龙皓, 邹男. 基于稀疏信号重构的阵元位置误差校正方法. 声学学报, 2017; 42(6): 677—684 DOI: 10.15949/j.cnki.0371-0025.2017.06.005 [13] Ferguson B G, Gray D A, Riley J L. Comparison of sharpness and eigenvector methods for towed array shape estimation. J. Acoust. Soc. Am., 1998; 91(3): 1565—1570 DOI: 10.1121/1.402437
[14] Smith J J, Leung Y H, Cantoni A. Broadband eigenvector methods for towed array shape estimation with a single source. IEEE International Conference on Acoustics, Speech, and Signal Processing, Atlanta, GA, USA, 1996: 3193—3196
[15] 汪俊, 吴立新, Lynch J, 等. 一种基于时延估计的双辅助声源阵形校准方法. 声学学报, 2007; 32(2): 165—170 DOI: 10.15949/j.cnki.0371-0025.2007.02.011 [16] 顾怡鸣, 宫在晓, 陈艳丽, 等. 浅海双基地有源探测调频信号直达波消除. 声学学报, 2022; 47(2): 187—197 DOI: 10.15949/j.cnki.0371-0025.2022.02.002 [17] 何心怡, 蒋兴舟, 李启虎, 等. 拖线阵的阵形畸变与左右舷分辨. 声学学报, 2004; 27(5): 409—413 DOI: 10.15949/j.cnki.0371-0025.2004.05.005 [18] Wu Q, Xu Y. A nonlinear data-driven towed array shape estimation method using passive underwater acoustic data. Remote Sens., 2022; 14(2): 304 DOI: 10.3390/rs14020304
[19] 张小凤, 张光斌. 双/多基地声呐系统. 北京: 科学出版社, 2014: 3—7 [20] 田坦. 声呐技术. 哈尔滨: 哈尔滨工程大学出版社, 2009: 18 [21] 范军, 卓琳凯. 水下目标回波特性计算的图形声学方法. 声学学报, 2006; 31(6): 511—516 DOI: 10.3321/j.issn:0371-0025.2006.06.006 [22] 陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用. 北京: 清华大学出版社, 2009: 12—19 [23] 宫在晓, 林京, 郭良浩. 浅海声传播相速度对测向精度的影响. 声学学报, 2002; 27(6): 492—496 DOI: 10.3321/j.issn:0371-0025.2002.06.003 -
期刊类型引用(1)
1. 王冠群,黄海宁,张舒然,迟骋,高善国,曾腾,张武. 基于吉布斯采样的方位自聚焦阵形校正方法. 网络新媒体技术. 2024(02): 45-52 .  百度学术
百度学术
其他类型引用(1)



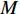
 下载:
下载: