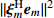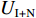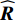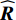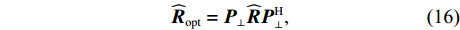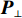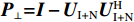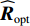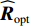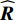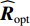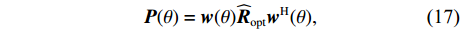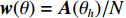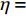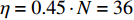Strong interference suppression for subspace judgment analysis
-
摘要:
针对海洋中存在的强干扰和环境噪声导致水下目标方位估计算法性能剧烈下降的问题, 提出了一种子空间判决分析的强干扰抑制方法(SSJ), 可实现多个强干扰下的目标方位估计。根据常规波束形成粗估的目标角度区间, 利用目标−干扰−噪声子空间与导向矢量的相关性, 设置判决项和估计合适的判决阈值来分离和抑制样本协方差矩阵中的非目标信息, 降低干扰和噪声的输出功率, 同时提高输出信干噪比, 为增强阵列的目标方位分辨能力提供方法支撑。仿真和海试数据处理结果显示, SSJ方法可抑制目标角度区间外的强干扰和噪声, 明显降低了干扰的输出功率和目标主瓣附近的旁瓣级, 提高了目标方位角度的分辨力。相比于现有的子空间干扰抑制方法, 所提方法具有更加稳健的干扰抑制能力。
Abstract:In the presence of strong underwater interferences, the performance of existing target of interest (TOI) bearing estimation algorithms significantly degrades. In this paper, a subspace judgment (SSJ)-based interference suppression method is proposed, which aims to enhance the ability of TOI-bearing estimation under multiple strong interferences. Specifically, with prior knowledge of the TOI bearing interval, the proposed method builds a judgment item exploiting the correlation between the TOI-interference-noise subspace and steering vector. Then the eigenvectors not dominated by the TOI can be accurately identified with a comparison of the aforementioned threshold. Finally, the identified ones will be subtracted from the sample covariance matrix (SCM). As a result, a residual SCM that primarily contains TOI is obtained, which provides methodical support for improving the capability of TOI-bearing resolution. Simulation and experimental results demonstrate that the method effectively suppresses strong interferences outside TOI-bearing intervals. It also reduces the output power of interference and sidelobe levels while improving the capability of TOI-bearing resolution. The proposed method outperforms other state-of-the-art subspace-based interference suppression methods.
-
Keywords:
- Subspace judgment /
- Judgment item /
- Judgment threshold /
- Interference suppression
-
引言
水下无源探测过程中, 强干扰和强噪声的存在导致水下目标方位估计算法的性能严重下降。特别是当干扰源的功率大于目标源的功率时, 强干扰往往会淹没目标, 从而影响水下目标方位估计的准确性。因此, 有效地抑制强干扰和强噪声, 提高目标的输出信干噪比, 是水下目标方位估计中的关键问题和研究重点。
空域矩阵滤波器是一种使用较为广泛的干扰抑制方法。它通过设置合适的通带和阻带来定义矩阵滤波器, 以实现对干扰的抑制, 并确保目标能够无失真地通过。在此方面, Vaccaro的工作为空域矩阵滤波器的设计奠定了基础[1]。随着研究的深入, 空域矩阵滤波器的设计和优化方法得到了进一步的发展。鄢社峰等[2]将滤波器的设计问题转化为凸优化问题, 为矩阵滤波器的设计提供了有效的解决方案。韩东等[3]引入Lagrange乘子理论和广义奇异值分解, 为宽带最优空域矩阵滤波器的设计提供了新的思路。梁国龙等[4-5]从信号加干扰子空间提取目标的特征分量, 为子区域多源检测提供了高效的解决方案。赵文彬等[6]通过K-L变换对矩阵进行降维处理, 构造了维数较低的矩阵滤波器。这些方法在干扰抑制方面取得了显著的效果, 但通常需要获得目标和干扰的已知或粗估角度的先验信息。
基于子空间类的干扰抑制方法也在不断发展中, 为解决实际应用中的复杂难题提供了更多选择。Kirsteins等[7]通过分解数据矩阵得到其主成分, 将干扰从数据中分离且去除, 以此来抑制干扰, 但是在信号功率相对波动以及动态变化引起目标和干扰相关特征向量的层次交换时该方法会存在一定的局限性。为解决此难题, 准确识别和确定数据矩阵的干扰分量, Harrison[8]利用目标和干扰的功率比形成判决项, 通过对每个特征向量进行分析, 自适应地识别和去除干扰子空间, 有效地抑制了与目标位置相近的干扰, 但需已知确切的目标角度, 且未给出具体的判决阈值, 同时干扰角度只选取与目标相邻的角度范围, 无法处理阵列端射方向的本舰噪声。针对此问题, 任岁玲等[9-10]在ECA的基础上, 通过设置目标角度区间, 给出了合适的判决阈值和判决准则, 对每个特征向量滤波处理, 自适应估计和去除非目标子空间, 更加稳健地抑制了干扰, 更适用于实际场景。然而, 在宽带处理中其判决准则会使目标子空间内存在较多的干扰和噪声分量, 导致旁瓣级较高。此外, Chen等[11]将基于特征分析的自适应干扰抑制方法(EAAIS)和卡尔曼滤波相结合进行联合干扰抑制和目标跟踪, 但需利用高分辨的DOA方法[12-13]减少干扰对目标跟踪的影响。除上述方法, 干扰抑制领域的其他研究, 如理论干扰预测的加权抑制[14]、多干扰抑制波束形成后的干扰抵消方法[15]等, 为海洋环境中强干扰和噪声的抑制提供了新的思路和解决方案。
针对上述问题, 提出了一种子空间判决分析的强干扰抑制方法(SSJ), 可应用于水下目标方位估计研究。SSJ方法根据粗估的目标角度区间, 利用非目标子空间和目标角度区间内的导向矢量的正交性来构造判决项, 通过设定适当的判决阈值来识别和分离出非目标子空间, 采用正交投影的方式去除样本协方差矩阵中的非目标信息, 从而抑制了目标角度区间外的强干扰和噪声, 提高了目标的输出信干噪比, 改善了多个强干扰下目标方位估计能力。仿真和海试数据处理结果表明, SSJ方法在抑制强干扰和提高目标方位角度分辨力方面的性能提升显著。
1. 基本理论
考虑
N 个传感器组成均匀水平直线阵, 相邻阵元间距为半波长d , 接收K 个从不同方向{θk}Kk=1 入射的信号, 其中有1个目标和K −1个干扰, 则阵列接收的数据建模为{\boldsymbol{x}}(t) ={\boldsymbol{ As}}(t) + {\boldsymbol{n}}(t), (1) 式中,
{\boldsymbol{A}}({\theta _k}) = {[1,{{\rm{e}}^{ - {\rm{j}}2\pi fd\cos \left( {{\theta _k}} \right)/c}}, \cdots ,{{\rm{e}}^{ - {\rm{j}}2\pi f\left( {N - 1} \right)d\cos \left( {{\theta _k}} \right)/c}}]^{\rm T}} 是对应于{\theta _k} 方向的阵列导向矢量,c 是声速,f 是信号频率,{\boldsymbol{A}} = [{\boldsymbol{A}}({\theta _1}), \cdots ,{\boldsymbol{A}}({\theta _k}), \cdots ,{\boldsymbol{A}}({\theta _K})] 是{{K}} 个目标的导向矢量矩阵,{\boldsymbol{s}}(t) = {[{{\boldsymbol{s}}_1}(t), \cdots ,{{\boldsymbol{s}}_k}(t), \cdots ,{{\boldsymbol{s}}_K}(t)]^{\rm T}} 为入射信号分量,{\boldsymbol{N }}={[{{\boldsymbol{n}}_1}(t), \cdots ,{{\boldsymbol{n}}_N}(t)]^{\rm T}} 是阵列接收到的噪声矩阵, 上标“T”表示矩阵转置。通过将样本协方差矩阵
{\boldsymbol{\widehat R}} 进行特征分解, 可得{{\widehat {\boldsymbol{R}} = }}\frac{1}{L}\sum\limits_{i = 1}^L {{ {\boldsymbol{x}_i}(t)} {\boldsymbol{x}_i}(t)^{\rm H}} {\boldsymbol{ = }}\sum\limits_{i = 1}^N {{\lambda _i}{{\boldsymbol{e}}_i}{\boldsymbol{e}}_i^{\rm H}} = \sum\limits_{i = 1}^K {{\lambda _i}{{\boldsymbol{e}}_i}{\boldsymbol{e}}_i^{\rm H}} + \sum\limits_{i = K{\boldsymbol{ + }}1}^N {{\lambda _i}{{\boldsymbol{e}}_i}{\boldsymbol{e}}_i^{\rm H}} , (2) 式中, 上标“H”表示共轭转置,
K 表示信源数,L 表示快拍数,{\boldsymbol{\widehat R}} 为N \times N 的复数矩阵,{\lambda _1},{\lambda _2}, \cdots ,{\lambda _N} 和{{\boldsymbol{e}}_1},{{\boldsymbol{e}}_2}, \cdots ,{{\boldsymbol{e}}_N} 分别为样本协方差矩阵{\boldsymbol{\widehat R}} 特征分解得到的特征值和特征向量, 且特征向量之间相互正交。特征值由大到小的顺序为{\lambda _1} > \cdots > {\lambda _d} > {\lambda _{d + 1}} > \cdots > {\lambda _N}. (3) 根据NE_AIC方法[16]来估计目标和干扰数目, 即基于随机矩阵理论(RMT)中MP律分析高斯白噪声下接收数据的样本噪声特征值, 再结合其统计特性和AIC准则来观测统计量。NE_AIC方法的信源数估计表达式为
\begin{split} {D_{{\rm{NE\_AIC}}}} =& \mathop {\arg {\rm{ min}}}\limits_D \frac{{{L^2}}}{2}{\left[ {\left( {N - D} \right)\frac{{\displaystyle\sum\limits_{i = D + 1}^N {\lambda _i^2} }}{{{{\left( {\displaystyle\sum\limits_{i = D + 1}^N {{\lambda _i}} } \right)}^2}}} - \left( {1 + \frac{N}{L}} \right)} \right]^2} + \\& 2\left( {D + 1} \right),\\[-12pt] \end{split} (4) 式中,
D 表示估计的信源数,{\lambda _i} 表示样本协方差矩阵的特征值,N 表示阵元数。经过NE_AIC方法的信源数估计, 当目标信噪比较大或快拍数足够大时, 将前
D 个大特征值对应的特征向量组成目标 − 干扰子空间(目标子空间和干扰子空间){{\boldsymbol{U}}_Z} , 剩余N - D 个小特征值对应的特征向量组成噪声子空间{{\boldsymbol{U}}_N} , 分别表示为{{\boldsymbol{U}}_Z} = \left[ {{{\boldsymbol{e}}_1},{{\boldsymbol{e}}_2}, \cdots ,{{\boldsymbol{e}}_D}} \right],\;\;{\boldsymbol{ }}{{\boldsymbol{U}}_N} = \left[ {{{\boldsymbol{e}}_{D + 1}},{{\boldsymbol{e}}_2}, \cdots ,{{\boldsymbol{e}}_N}} \right]. (5) 根据式(5), NE_AIC方法估计信源数
D = K , 目标和干扰的特征向量可表示为对应导向矢量的单位标准基, 即目标和干扰张成的子空间与导向矢量张成的子空间存在包含关系, 而噪声分量张成的噪声子空间与导向矢量张成的空间相互正交, 满足{\boldsymbol{span}}\left\{ {{{\boldsymbol{e}}_1},{{\boldsymbol{e}}_2}, \cdots ,{{\boldsymbol{e}}_D}} \right\} \simeq {\boldsymbol{span}}\left\{ {{\boldsymbol{A}}({\theta _1}),{\boldsymbol{A}}({\theta _2}), \cdots ,{\boldsymbol{A}}({\theta _D})} \right\}, (6) {\boldsymbol{span}}\left\{ {{{\boldsymbol{e}}_{D + 1}},{{\boldsymbol{e}}_{D + 2}}, \cdots ,{{\boldsymbol{e}}_N}} \right\} \bot {\boldsymbol{span}}\left\{ {{\boldsymbol{A}}({\theta _1}),{\boldsymbol{A}}({\theta _2}), \cdots ,{\boldsymbol{A}}({\theta _D})} \right\}. (7) 目标或干扰在
{\theta _g} 方向处对应的导向矢量可表示为{\boldsymbol{A}}({\theta _g}) \simeq {{\boldsymbol{e}}_g}{\boldsymbol{e}}_g^{\rm H}{\boldsymbol{A}}({\theta _g}). (8) 将式(8)等号两侧同时乘以
{\boldsymbol{A}}{({\theta _g})^{\rm H}} , 根据{\boldsymbol{A}}{({\theta _g})^{\rm H}}{\boldsymbol{A}}({\theta _g}) = N 及式(6)和式(7), 可得N \simeq {\left\| {{\boldsymbol{A}}{{({\theta _g})}^{\rm H}}{{\boldsymbol{e}}_g}} \right\|^2},\;\;{\left\| {{\boldsymbol{A}}{{({\theta _g})}^{\rm H}}{{\boldsymbol{e}}_j}} \right\|^2} \simeq 0, (9) 式中,
\left\| \cdot \right\| 表示欧几里得范数,{{\boldsymbol{e}}_g} 表示干扰和目标的特征向量,g \in [1,D] ,D 为干扰和目标总数;{{\boldsymbol{e}}_j} 表示噪声特征向量,j \in [D + 1,N] , 且j \ne g 。当目标信噪比低或快拍数不足时, NE_AIC方法估计的信源数
D < K , 故{U_Z} 内不一定包含目标分量, 从而导致子空间泄露问题, 致使特征向量出现“相变”现象, 使{\| {{\boldsymbol{A}}{{({\theta _g})}^{\rm H}}{{\boldsymbol{e}}_g}} \|^2} < N , 为此形成干扰子空间、目标 − 噪声子空间(目标子空间和噪声子空间), 这为后文中建立判决阈值与快拍数、阵元数和基于接收信号的信噪比的关系提供了前提。2. 子空间判决分析的干扰抑制理论
首先通过常规波束形成(CBF)估计出目标的先验信息, 粗估目标角度
{\theta _0} , 预设目标角度区间为[{\theta _{S1}},{\theta _{S2}}] , 满足{0{\text °}} \leqslant {\theta _{S1}} < {\theta _0} < {\theta _{S2}} \leqslant {180{\text °}} , 其角度区间的网格大小设为0.1°, 共Q = ({\theta _{S2}}{\boldsymbol{ - }}{\theta _{S1}})/0.1 + 1 个值。构造Q 个导向矢量, 即\begin{split} {\boldsymbol{A}}({\theta _q}) =& {[1,{{\rm{e}}^{ - {\rm{j}}2\pi fd\cos \left( {{\theta _q}} \right)/c}}, \cdots ,{{\rm{e}}^{ - {\rm{j}}2\pi f\left( {N - 1} \right)d\cos \left( {{\theta _q}} \right)/c}}]^{\rm T}},\\&{\theta _q} \in [{\theta _{S1}},{\theta _{S2}}], \end{split} (10) 式中,
{\boldsymbol{A}}({\theta _q}) 为N × 1的导向矢量,q \in [1,Q] ,[{\theta _{S1}},{\theta _{S2}}] 区间内形成的导向矢量矩阵为{\boldsymbol{A}} = [{\boldsymbol{A}}({\theta _1}), \cdots ,{\boldsymbol{A}}({\theta _q}), \cdots ,{\boldsymbol{A}}({\theta _Q})], (11) 式中,
{\boldsymbol{A}} 为Q 个角度的导向矢量矩阵, 维数为{{N}} \times {{Q}} 。基于目标导向矢量与所对应特征向量相乘最大, 且与其他特征向量相乘为零的性质, 在粗估目标角度区间构造一个判决项, 将
Q 个导向矢量在两个子空间内遍历, 寻找两个子空间内的目标分量。判决项如下:{\boldsymbol{D}}{{\boldsymbol{F}}_{ii}} = \mathop {\mathop {\max }\limits_{{\theta _q} \in [{\theta _{S1}},{\theta _{S2}}]} }\limits_{l \in [1,N]} {\boldsymbol{ }}{\left\| {{\boldsymbol{A}}{{({\theta _q})}^{\rm H}}{{\boldsymbol{e}}_l}} \right\|^2},\;\;ii \in [1,N], (12) 式中,
{\boldsymbol{D}}{{\boldsymbol{F}}_{ii}} 表示目标角度区间内导向矢量与子空间中特征向量匹配的结果,{\boldsymbol{A}}({\theta _q}) 表示目标粗估角度对应的导向矢量, 为N\times 1 的复数向量,{\boldsymbol{e}}_{l} 表示样本协方差矩阵{\boldsymbol{\widehat R}} 特征分解的第l 个特征分量, 每个特征向量为N\times 1 的复数向量。将估计的判决阈值
\eta 与判决项进行比较, 分离出干扰 − 噪声子空间(干扰子空间和噪声子空间)。若{\boldsymbol{D}}{{\boldsymbol{F}}_{ii}} \geqslant \eta , 则表示两个子空间内有目标分量, 剩余的干扰分量和噪声分量可组成干扰 − 噪声子空间; 若{\boldsymbol{D}}{{\boldsymbol{F}}_{ii}} < \eta , 则表示两个子空间无目标分量, 只存在干扰分量和噪声分量, 为此两个子空间直接合并组成干扰 − 噪声子空间。在宽带处理过程中, 为了保证在所选频带范围内尽可能将目标分量分离到目标子空间, 且将多余的干扰分量和噪声分量分离到干扰 − 噪声子空间内。判决阈值需满足式(13)所示的条件, 此方式的优势是只需计算出
{\| {{\boldsymbol{A}}{{({\theta _s})}^{\rm H}}{{\boldsymbol{e}}_n}} \|^2} 的最大值作为判决阈值, 即可认为目标子空间内仅有目标分量和少量的噪声分量。{\left\| {{\boldsymbol{A}}{{({\theta _s})}^{\rm H}}{{\boldsymbol{e}}_s}} \right\|^2} > {\left\| {{\boldsymbol{A}}{{({\theta _s})}^{\rm H}}{{\boldsymbol{e}}_n}} \right\|^2}, (13) 式中,
{\boldsymbol{A}}({\theta _s}) 为目标对应的导向矢量,{{\boldsymbol{e}}_s} 为目标对应的特征向量,{{\boldsymbol{e}}_n} 为干扰和噪声对应的特征向量。在小快拍和低信噪比条件下, 样本协方差矩阵和理想协方差矩阵存在较大的偏差[17-18], 使其子空间泄露, 样本特征向量出现“相变”现象[19-20], 从而导致
{\Vert \boldsymbol{A}{({\theta }_{s})}^{{\rm H}}{\boldsymbol{e}}_{s}\Vert }^{2} < {\Vert \boldsymbol{A}{({\theta }_{s})}^{{\rm H}}{\boldsymbol{e}}_{n}\Vert }^{2} 的问题。对此, 文献[21]中给出了基于RMT理论的阵元数、快拍数及基于接收信号估计的信噪比对判决阈值的影响, 表达式如下:{\cos ^2}\left( {{\xi _m},{{\boldsymbol{e}}_m}} \right)\mathop \to \limits^{\rm a.s.} \left\{ \begin{array}{ll} 0{\boldsymbol{ , }}&N\dfrac{{\sigma _m^2}}{{\sigma _n^2}} \leqslant \sqrt C , \\ \dfrac{{1 - C{{\left( {\dfrac{{\sigma _n^2}}{{N\sigma _m^2}}} \right)}^2}}}{{1 + C\dfrac{{\sigma _n^2}}{{N\sigma _m^2}}}}{\boldsymbol{ , }}& N\dfrac{{\sigma _m^2}}{{\sigma _n^2}} > \sqrt C , \\ \end{array} \right. (14) 式中,
{\xi _m} 为理想特征向量,{{\boldsymbol{e}}_m} 为实际特征向量,\sigma _m^2 为信号功率,\sigma _n^2 为噪声功率, 信噪比{R_{{\rm{SN}}}} = \sigma _m^2/\sigma _n^2 ,C = N/L 为阵元数N与快拍数L的比值。基于式(6)和式(8)的性质, 可得理想特征向量
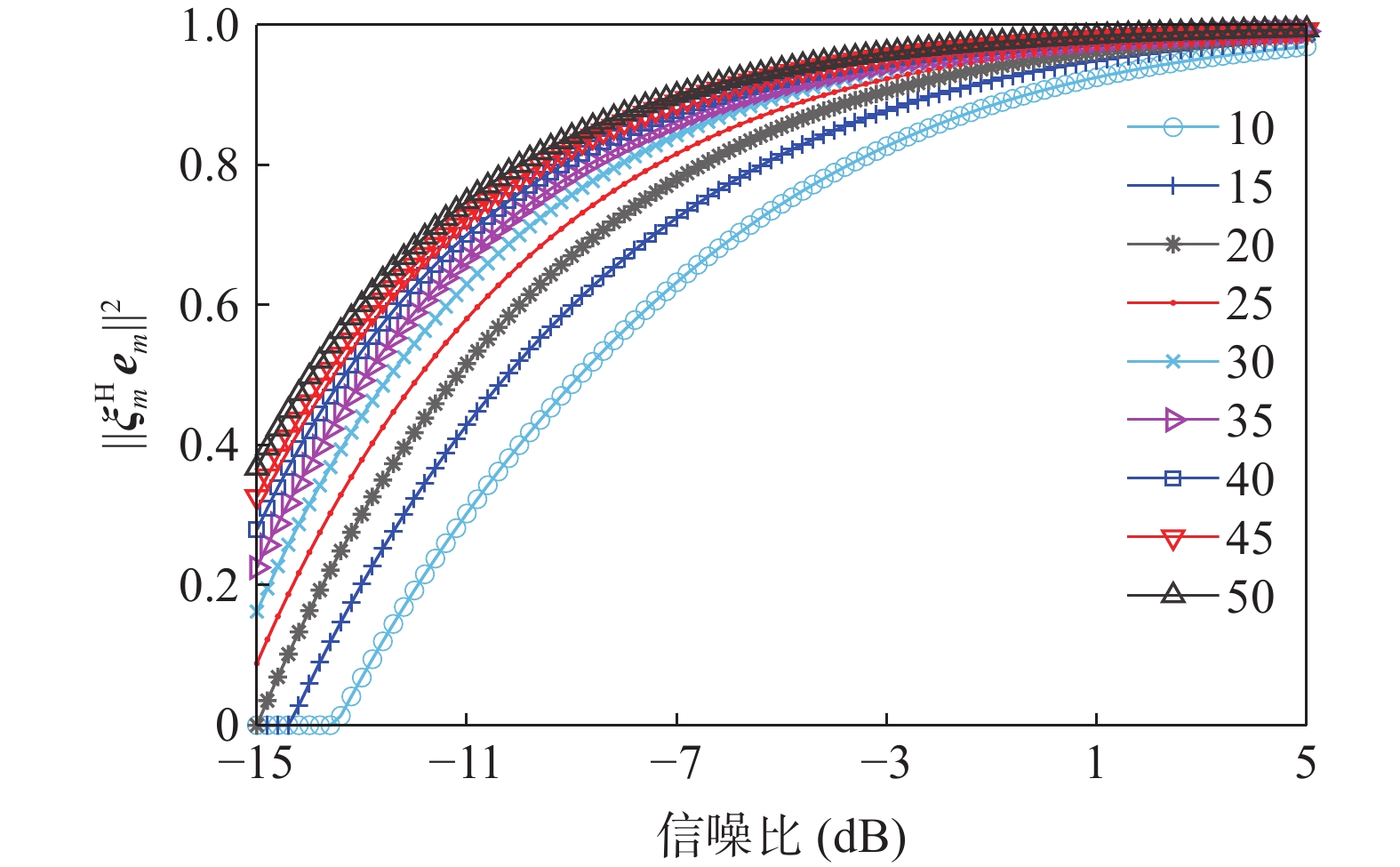
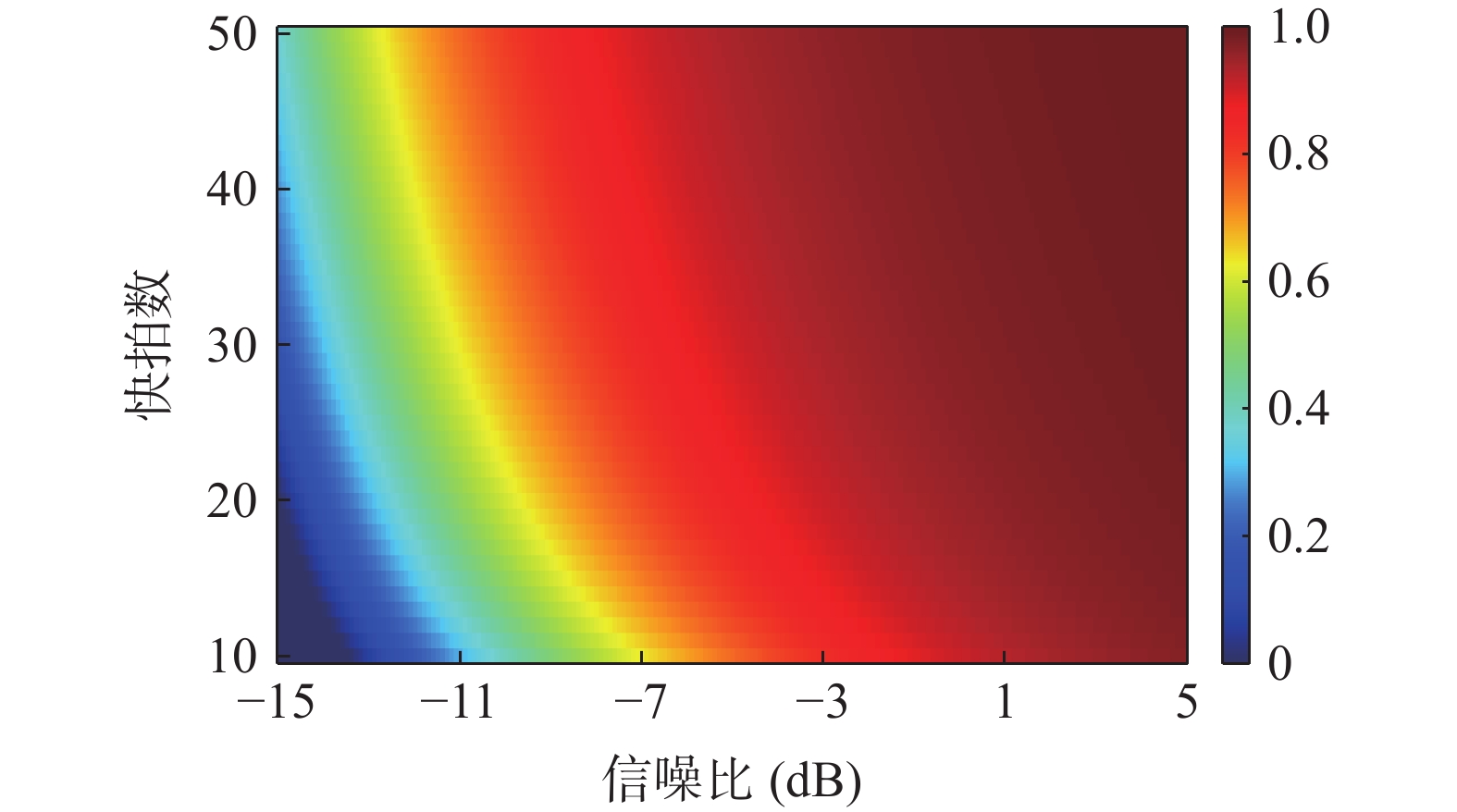
{\xi _m} 为导向矢量的标准基, 即{\xi _m} = {\boldsymbol{A}}({\theta _m})/\sqrt N 。根据文献[22], 可将式(14)变为{\left\| {{\boldsymbol{A}}{{({\theta _m})}^{\rm H}} {{\boldsymbol{e}}_m}} \right\|^2}\mathop \to \limits^{\rm a.s.} \left\{ \begin{array}{ll} {\boldsymbol{ }}0{\boldsymbol{ }},&{\boldsymbol{ }}N \cdot {R_{\rm{SN}}} \leqslant \sqrt C , \\ \dfrac{{1 - C{{\left( {\dfrac{1}{{N \cdot {R_{\rm{SN}}}}}} \right)}^2}}}{{\sqrt N \cdot \left( {1 + C\dfrac{1}{{N \cdot {R_{\rm{SN}}}}}} \right)}}{\boldsymbol{ }},&{\boldsymbol{ }}N \cdot {R_{\rm{SN}}} > \sqrt C . \\ \end{array} \right.{\boldsymbol{ }} (15) 由于实际中难以获取目标的信噪比, 本文通过建立仿真模型, 固定阵元数, 研究不同信噪比和不同快拍数下判决阈值的变化情况。仿真条件如下: 阵元数50, 信噪比−15~5 dB, 快拍数10~50, 图1和图2为快拍数和信噪比变化时
{\| {{\boldsymbol\xi} _m^{\rm H} {{\boldsymbol{e}}_m}} \|^2} 值的仿真结果。{\| {{\boldsymbol\xi} _m^{\rm H} {{\boldsymbol{e}}_m}} \|^2} 值随着快拍数和信噪比的变化而变化, 当同时满足高信噪比和足够快拍数时,{\| {{\boldsymbol\xi} _m^{\rm H} {{\boldsymbol{e}}_m}} \|^2} 值接近于1, 且相对稳定; 当足够快拍数或高信噪比仅满足一项时,{\| {{\boldsymbol\xi} _m^{\rm H} {{\boldsymbol{e}}_m}} \|^2} 值较高, 最大可接近于1; 但当信噪比较低和小快拍数时, 子空间出现严重泄露, 导致{\| {{\boldsymbol\xi} _m^{\rm H} {{\boldsymbol{e}}_m}} \|^2} 值较低, 特别是信噪比和快拍数非常低的情况, 其值接近于0。为此, 根据式(15)中的阵元数、快拍数和基于接收信号估计的信噪比来选取合适的判决阈值。通过此方式的阈值选取, 可保证{\| {{\boldsymbol{A}}{{({\theta _s})}^{\rm H}}{{\boldsymbol{e}}_s}} \|^2} > {\| {{\boldsymbol{A}}{{({\theta _s})}^{\rm H}}{{\boldsymbol{e}}_n}} \|^2} , 使目标子空间内尽可能仅有目标分量和少量干扰分量及噪声分量。实际上, 基于接收信号估计的信噪比很难直接获取, 为此通过CBF估计出的结果来粗估基于接收信号估计的信噪比, 进而估计出判决阈值, 通过与判决项的比较实现强干扰的抑制。
通过式(12)和式(13)的判决项和判决阈值的分离方法, SSJ方法利用正交投影方式将干扰 − 噪声子空间
{U_{\rm{I} + {\rm{N}}}} 从样本协方差矩阵{\boldsymbol{\widehat R}} 中删除, 重构样本协方差矩阵{\boldsymbol{\widehat R}} , 即{{\boldsymbol{\widehat R}}_{\rm opt}} = {{\boldsymbol{P}}_ \bot }{\boldsymbol{\widehat R}}{\boldsymbol{P}}_ \bot ^{\rm H}, (16) 式中,
{{\boldsymbol{P}}_ \bot } 为干扰 − 噪声子空间的正交投影矩阵, 即{{\boldsymbol{P}}_ \bot }{{ = }}{\boldsymbol{I}} - {{\boldsymbol{U}}_{{\rm{I}} + {\rm{N}}}}{\boldsymbol{U}}_{\rm{I} + {\rm{N}}}^{\rm H} 。将已重构的样本协方差矩阵
{{\boldsymbol{\widehat R}}_{{\rm{opt}}}} 应用于方位估计, 获取更可靠的目标角度参数。将式(16)中{{\boldsymbol{\widehat R}}_{{\rm{opt}}}} 替代式(2)中的{\boldsymbol{\widehat R}} , 利用{{\boldsymbol{\widehat R}}_{{\rm{opt}}}} 进行空间谱估计, 可抑制强干扰和噪声:{\boldsymbol{P}}(\theta ) = {\boldsymbol{w}}(\theta ){{\boldsymbol{\widehat R}}_{{\rm{opt}}}}{{\boldsymbol{w}}^{\rm H}}(\theta ), (17) 式中,
{\boldsymbol{w}}(\theta ) = {\boldsymbol{A}}({\theta _h})/N ,{\theta _h} \in [{0{\text{°}}}{\boldsymbol{,}}\;{180{\text{°}}}] 。3. 仿真与性能分析
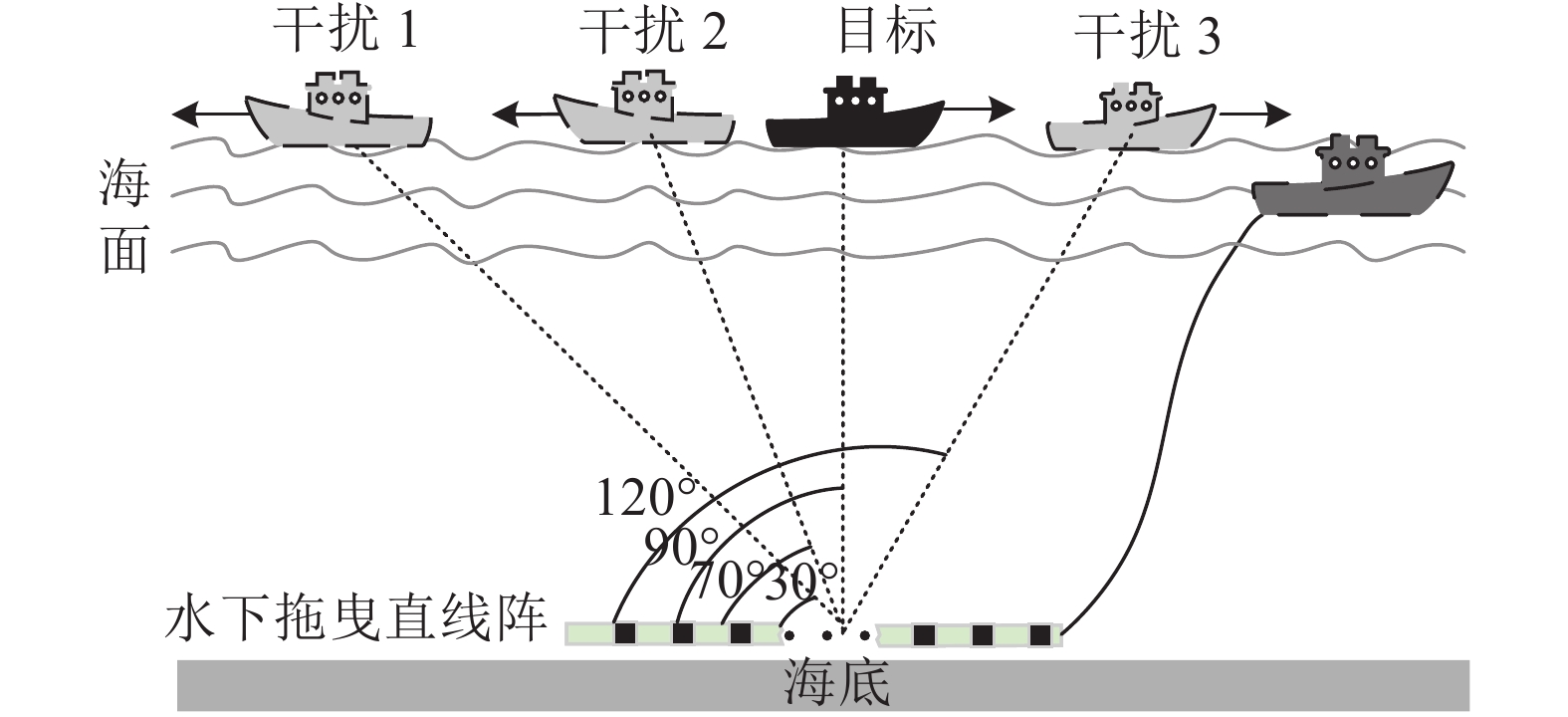
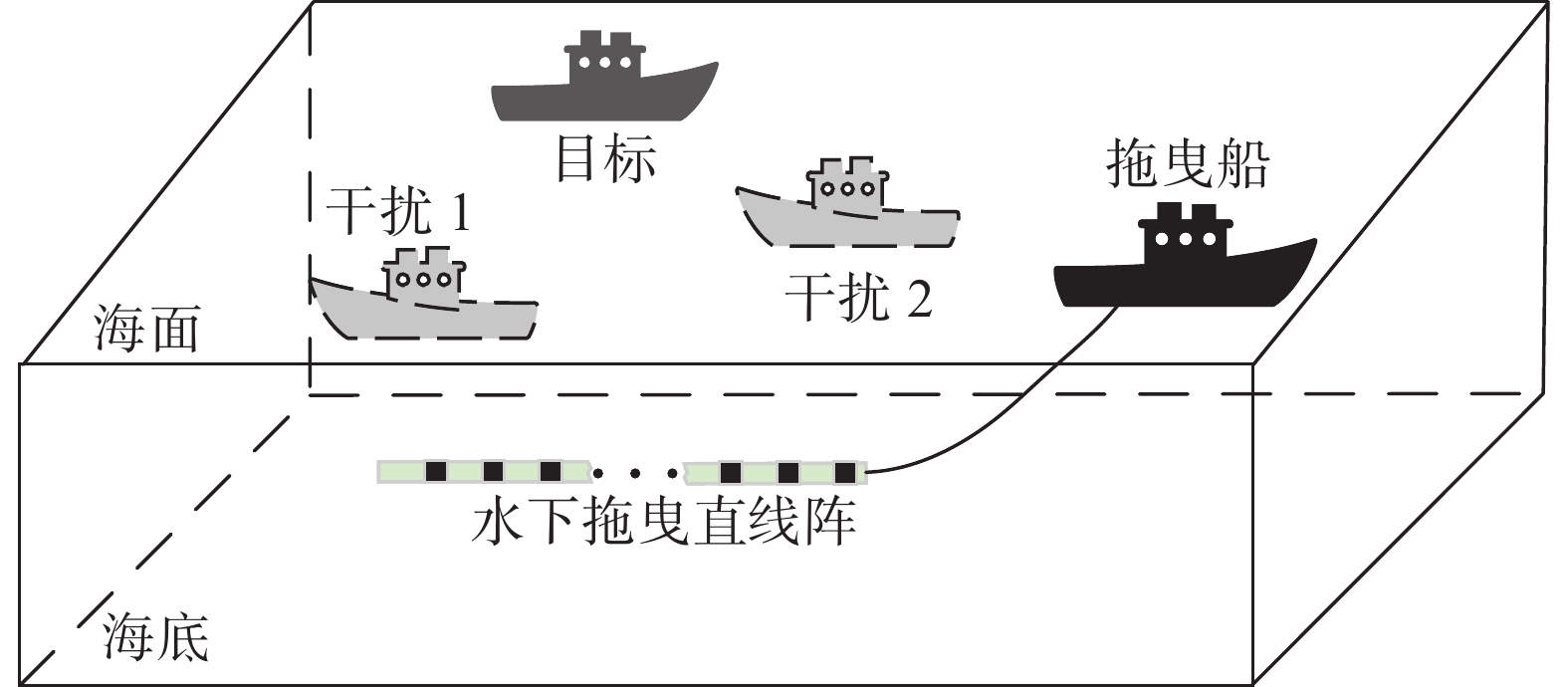
仿真环境参数设置如下: 水下拖曳直线阵的阵元数为50, 阵元间距为半波长, 阵列接收4个带宽为400 Hz、中心频率为300 Hz的宽带信号, 且各信号互不相关, 信噪比分别为15 dB, 11 dB, −4 dB, 13 dB, 其中−4 dB为目标的信噪比, 其余3个设置为干扰, 噪声为与信号不相关的高斯白噪声。仿真数据的总长度约为8.1 s, 信号采样率为3 kHz, 共25600个点, 其中数据重叠率设为50 %, 快拍数为39, 角度扫描间隔为0.1°。水下拖曳直线阵无源探测仿真实验示意图如图3所示, 图中标示的角度为强干扰和目标初始角度, 箭头表示强干扰和目标运动方向。
为了更好地分析水下拖曳直线阵无源探测仿真实验, 将其分为3部分进行分析, 第1部分中水下拖曳直线阵处于静止状态, 仅有目标运动; 第2部分中强干扰和目标与水下拖曳直线阵处于相对运动状态; 第3部分中强干扰处于阵列端射方向以模拟水下拖曳直线阵的本舰干扰, 并且其他强干扰和目标与水下拖曳直线阵处于相对运动状态。
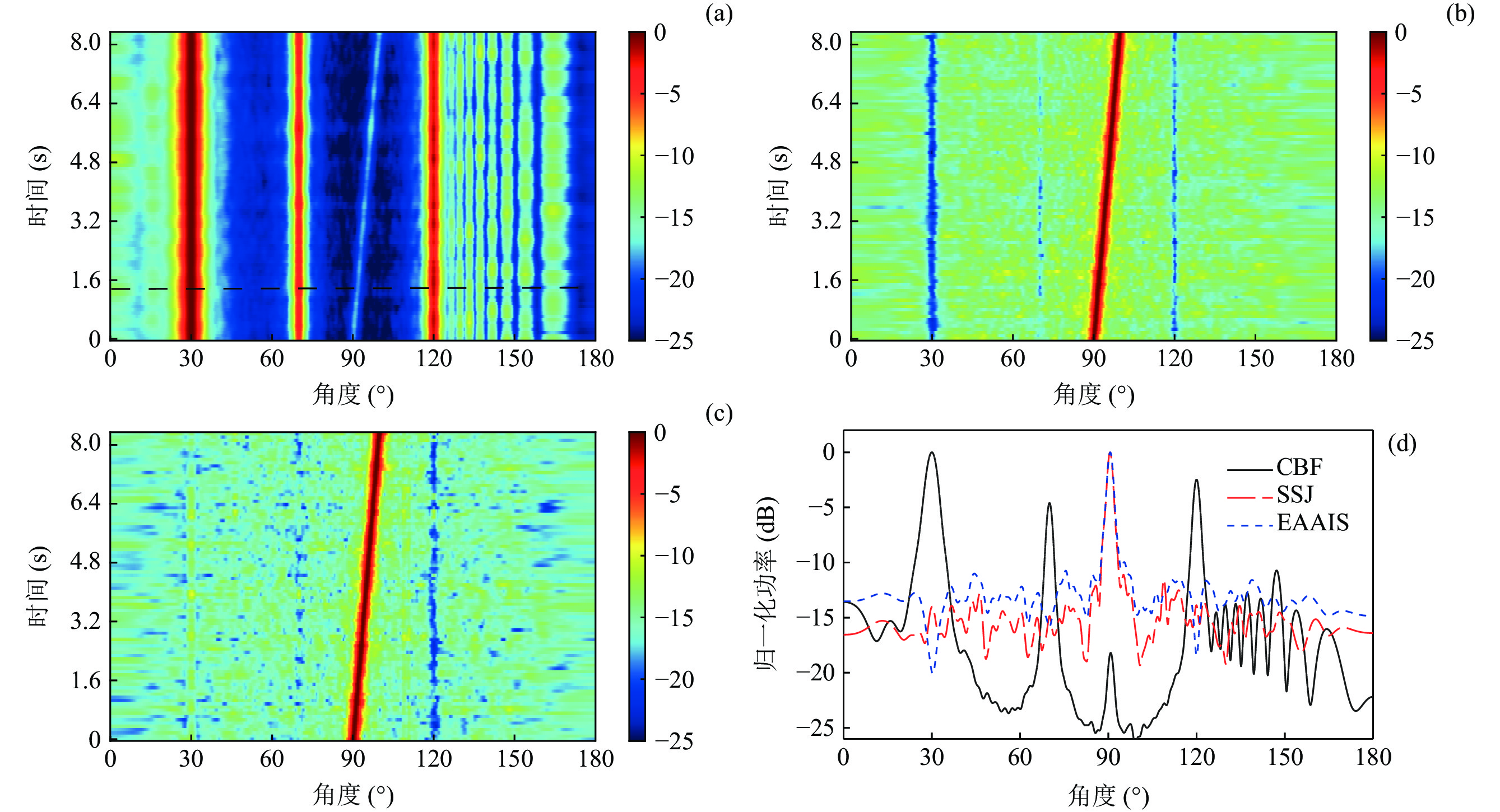
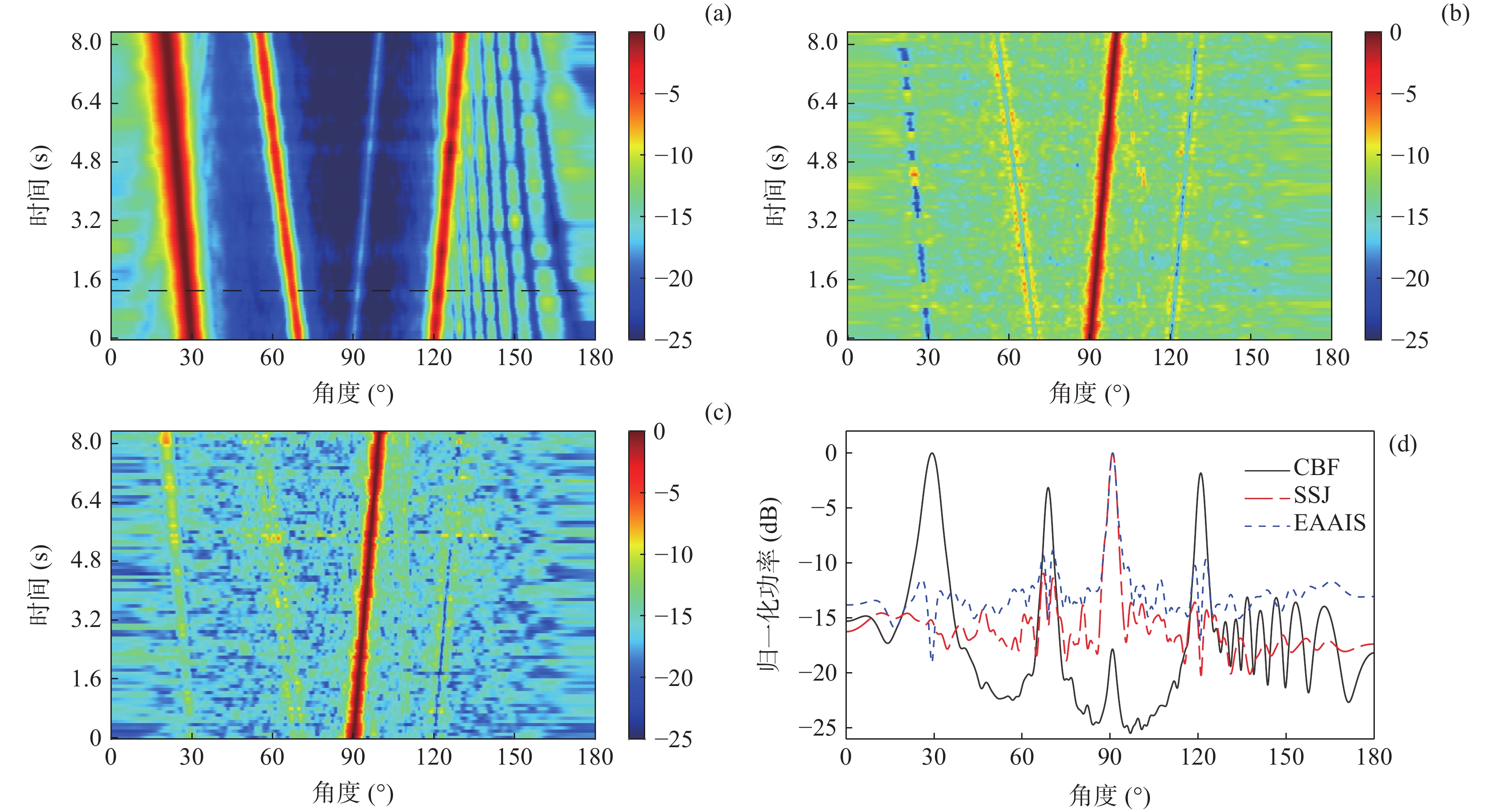
当仅有目标运动时, 图4(a)表示经CBF处理后的方位历程图, 目标从90°运动到100°, 其强度最低; 而在30°位置, 干扰强度最高, 并高于其他角度的干扰。图4(b)表示经EAAIS方法干扰抑制后的方位历程图, 明显看出EAAIS方法不受目标运动带来的影响, 只需确保粗估角度区间覆盖目标的运动范围, 就能很好地抑制强干扰和噪声。图4(c)为SSJ方法的处理结果, 根据式(13)的处理方式, SSJ方法能够减少干扰和噪声分量泄露到目标子空间, 而尽可能全部分离到干扰 − 噪声子空间内, 有效地抑制干扰和噪声。在120°位置, 干扰的输出功率与EAAIS方法相当, 目标主瓣附近85°处的旁瓣级最大低于EAAIS方法5 dB。然而, 在30°位置, 干扰的输出功率比EAAIS方法高约4 dB, 这是由于判决阈值参数未能全时间段自适应, 导致干扰未被完全抑制。通过图4(d)的单个时间点的归一化功率谱估计结果可知, 相比于EAAIS方法, 在相同主瓣宽度下, SSJ方法在目标主瓣附近的旁瓣级最大降低了4 dB。然而, 由于判决阈值未实现全时间段自适应, 导致干扰抑制效果未达最优。
当强干扰和目标同时运动且无交叉时, 经CBF处理后的方位历程如图5(a)所示, 目标从90°运动到100°, 其强度最低; 三个强干扰分别从30°运动到20°、从70°运动到55°和从120°运动到130°, 其中初始位置30°处的干扰强度最大, 略高于其他角度处的干扰。图5(b)所示为经EAAIS方法处理后的结果, EAAIS方法不受强干扰和目标运动带来的影响, 同样只需确保角度区间覆盖目标的运动范围, 即可很好地抑制强干扰和噪声。而SSJ方法处理的结果如图5(c)所示, SSJ方法也能抑制大部分噪声分量和干扰分量。在120°位置, 干扰的输出功率比EAAIS方法低约3 dB, 目标主瓣附近85°处的旁瓣级比EAAIS方法最大低5 dB。然而, 在30°位置, 干扰的输出功率比EAAIS方法高约4 dB, 这是由于判决阈值的参数没有达到全时间段自适应, 导致干扰未能被完全抑制。从图5(d)的单个时间点的归一化功率谱估计结果中更容易看出, 相比于EAAIS方法, SSJ方法在目标主瓣附近85.5°处的旁瓣级降低了约5 dB, 干扰的输出功率降低了2 dB。
当强干扰处于端射方向并持续存在时, CBF处理后的方位历程如图6(a)所示, 目标从90°运动到100°, 其强度最低。端射方向(小于10°和大于170°)存在两个强干扰, 其强度略低于70°运动到50°的干扰。图6(b)所示为经EAAIS方法处理后的结果, EAAIS方法依然只需确保角度区间覆盖目标的运动范围, 即可抑制端射方向和其他角度的强干扰。SSJ方法处理结果如图6(c)所示, SSJ方法在此场景依然能抑制大部分干扰和噪声分量。在170°位置, 干扰的输出功率比EAAIS方法低约2 dB, 在10°处干扰的输出功率与EAAIS方法相差无几, 而目标主瓣附近82°处的旁瓣级比EAAIS方法低约4 dB。因此, SSJ虽然能够抑制各个角度处的强干扰和噪声, 但判决阈值的估计依然致使未能很好地抑制全时段阵列端射方向的干扰。从图6(d)的单个时间点的归一化功率谱估计结果中看出, 相比于EAAIS方法, 在相同主瓣宽度时, SSJ方法在目标主瓣附近81.5°处的旁瓣级降低了约5 dB, 干扰的输出功率也降低了约2 dB。
4. 海试数据处理及结果分析
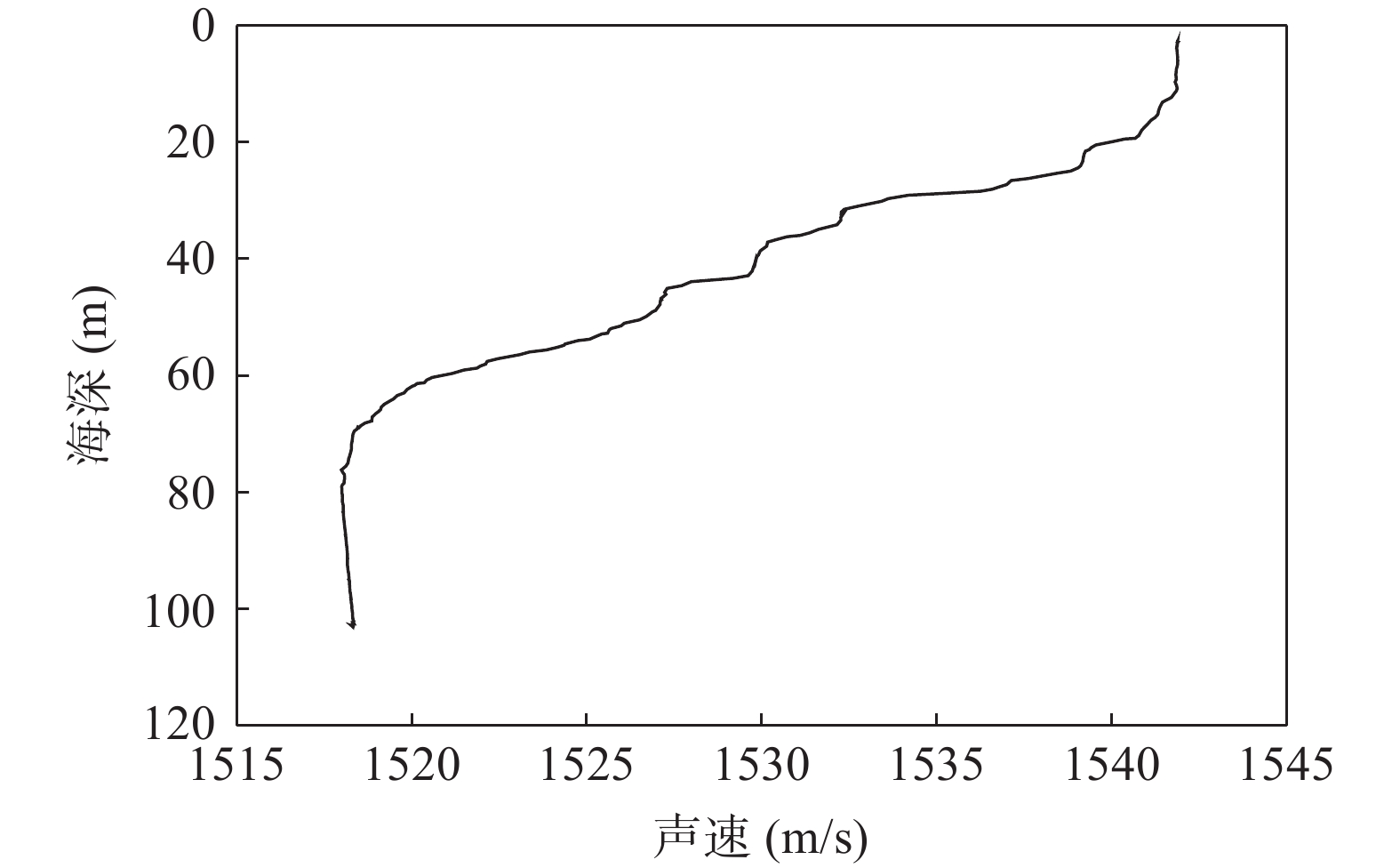
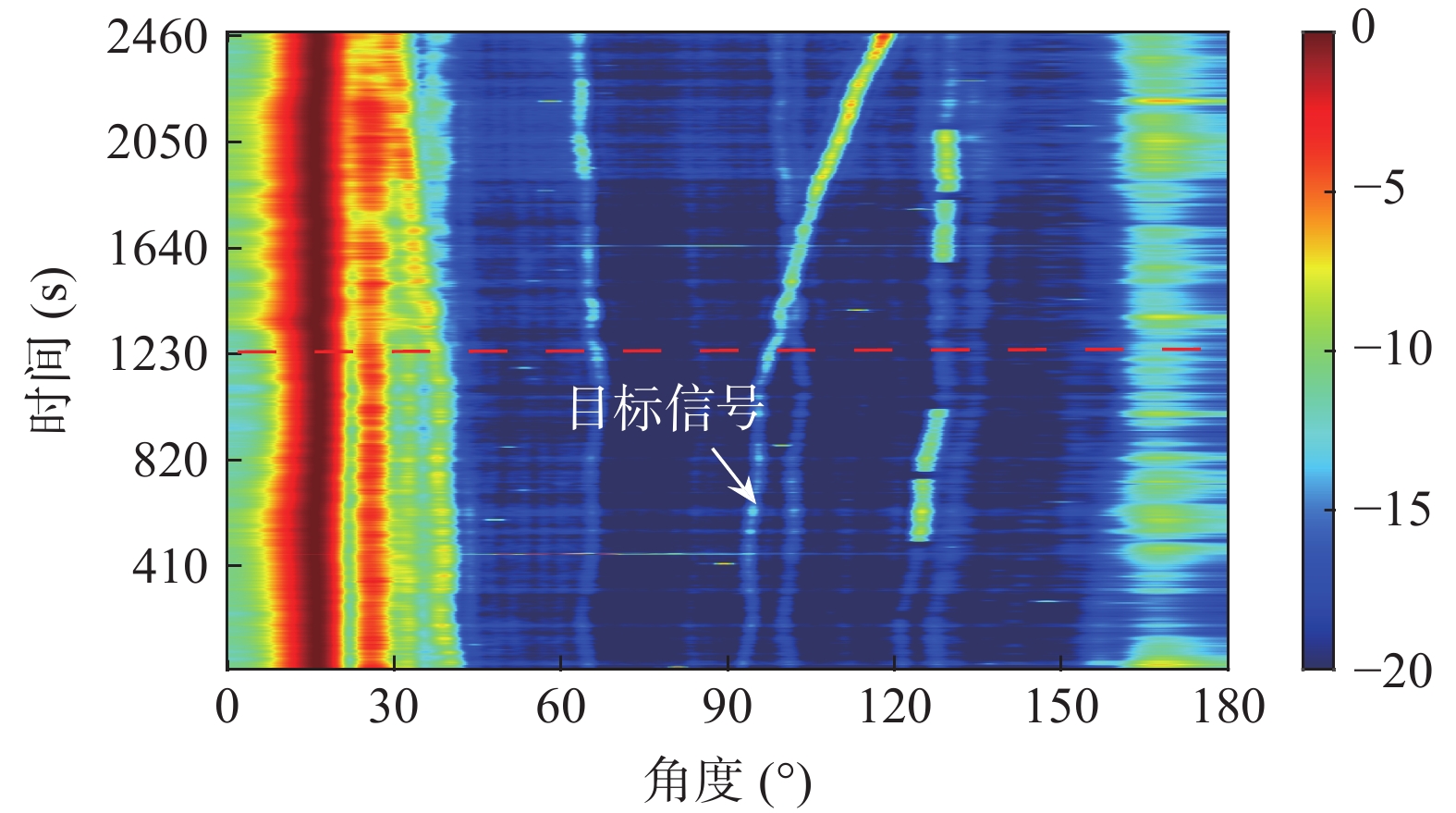
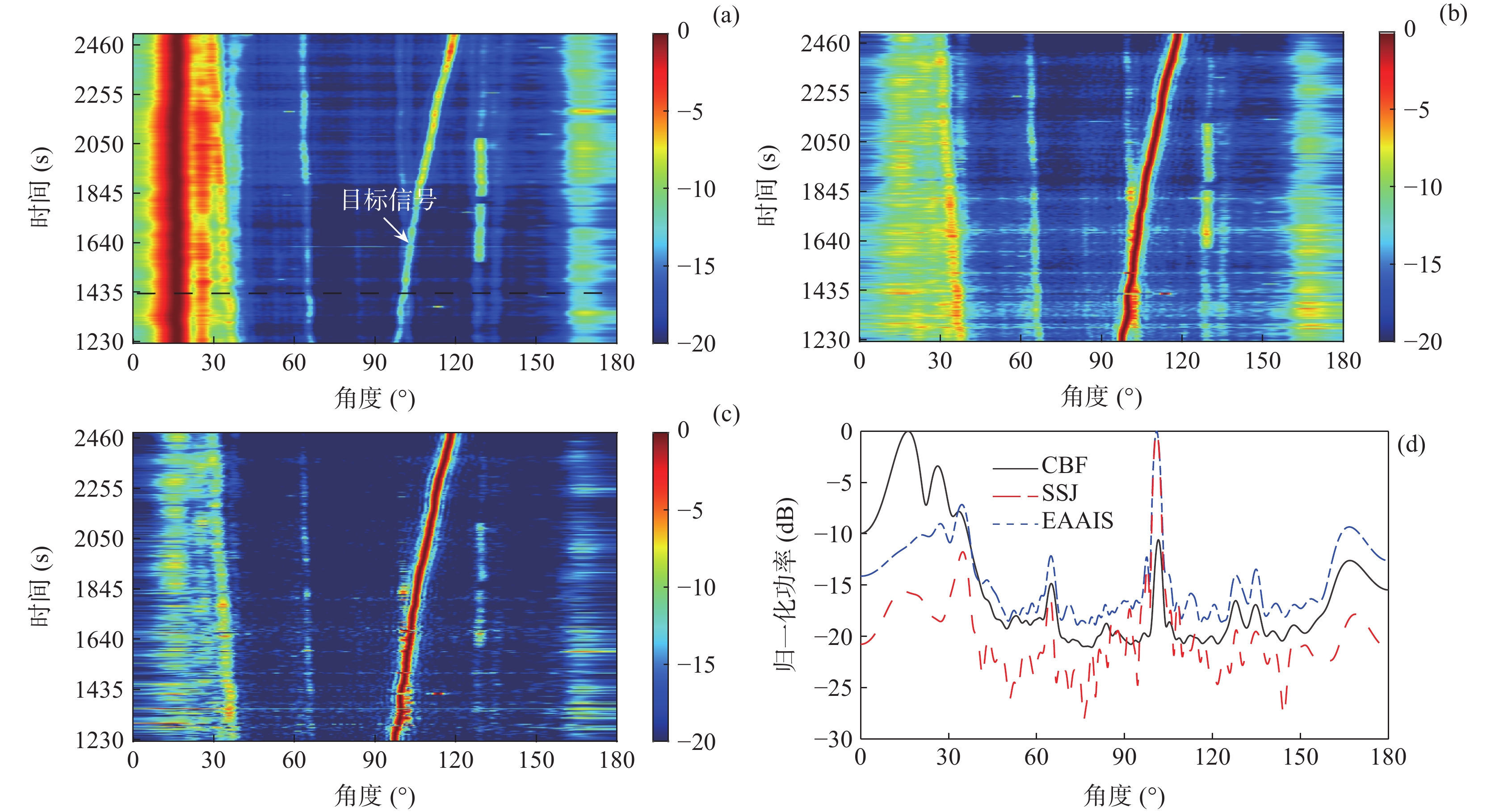
通过处理海试中水下拖曳直线阵列接收的目标和干扰数据, 分析和验证所提出的子空间判决分析的强干扰抑制方法在实际水下目标方位估计中的可行性。2021年7月, 哈尔滨工程大学在南海浅海区域进行了一次水下拖曳直线阵无源探测实验。实验海区水深约102 m, 水中声速剖面如图7所示, 在水下3~10 m之间存在一个等温层, 水下10~76 m之间存在一个温跃层, 为典型的夏季浅海水文条件。水下拖曳直线阵阵元数为80, 相邻阵元间距为2 m, 拖曳速度为6 kn, 阵元深度为99 m。数据的频率范围为180~280 Hz, 共101个频点, 采样频率为8 kHz, 处理的数据长度为60 s, 每6 s进行一次频域采样, 数据重叠率为50%, 合计10个快拍; 接收阵所在深度的水中声速为1518 m/s, 角度搜索间隔为0.1°。根据实验前的标记, 目标初始角度大约为90°, 如图8所示。
根据式(15)的分析, 判决阈值与快拍数、阵元数和基于接收估计信号的信噪比相关。为了更好地处理数据和估计判决阈值, 根据目标功率的不同将整个历程划分为两部分。图9为经CBF处理后的整个时间方位历程图, 其中红色虚线表示两部分历程的分界处, 白色箭头指向的位置为目标的整体轨迹。在阵列拖曳过程中, 端射方向的本舰干扰强度大, 并持续存在于小于30°和大于160°的位置。第1部分历程中, 目标从约95°开始相对阵列运动, 其功率逐渐增强。在此时间段, 本舰干扰强度较大, 且在第8分钟至第17分钟之间, 约在120°处存在一段较强的干扰; 第2部分历程中, 目标从约100°相对运动至约120°, 其功率逐渐增强, 与此同时, 本舰干扰仍然存在, 并且在约130°处存在约9 min的较强干扰。
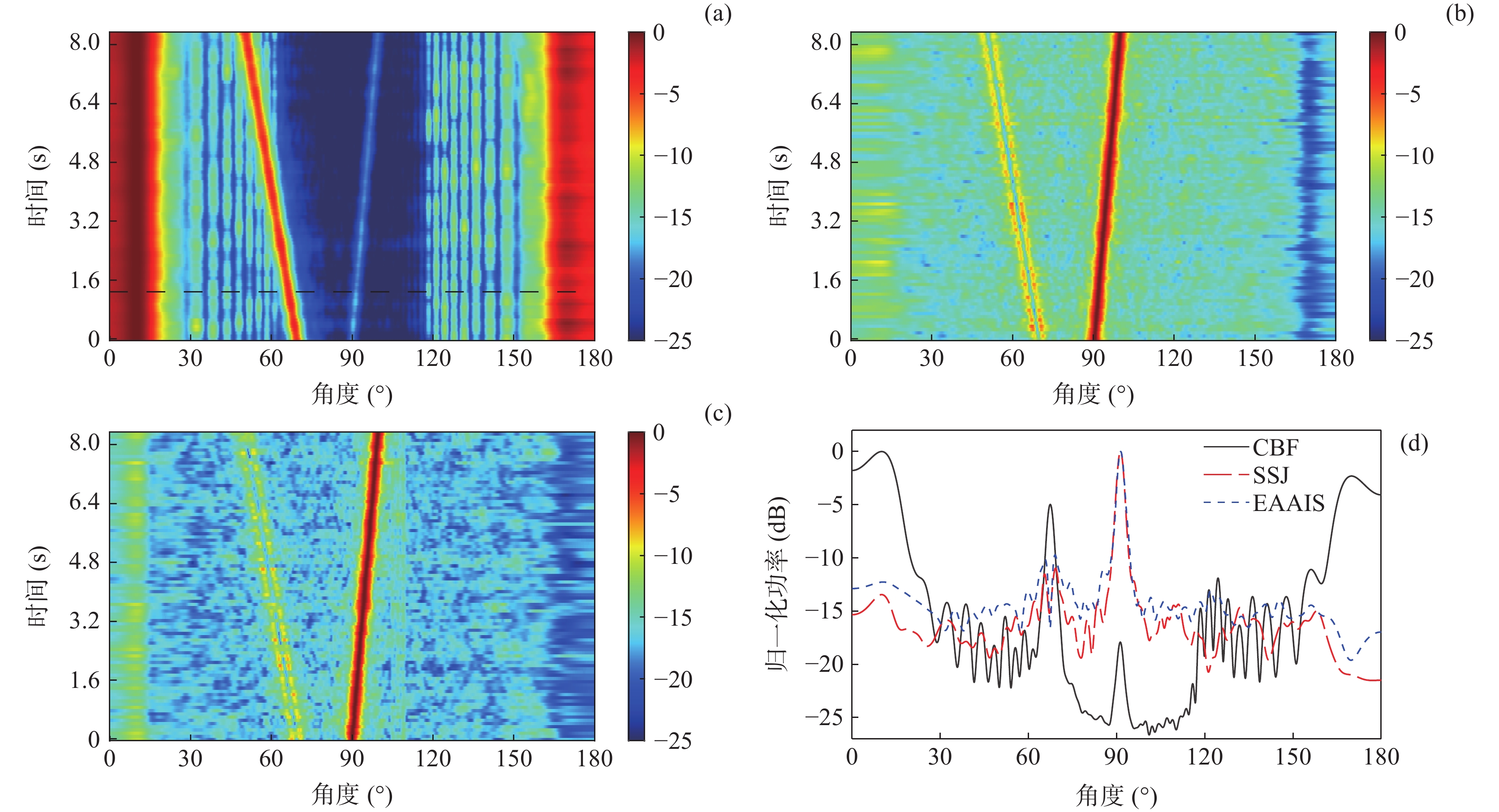
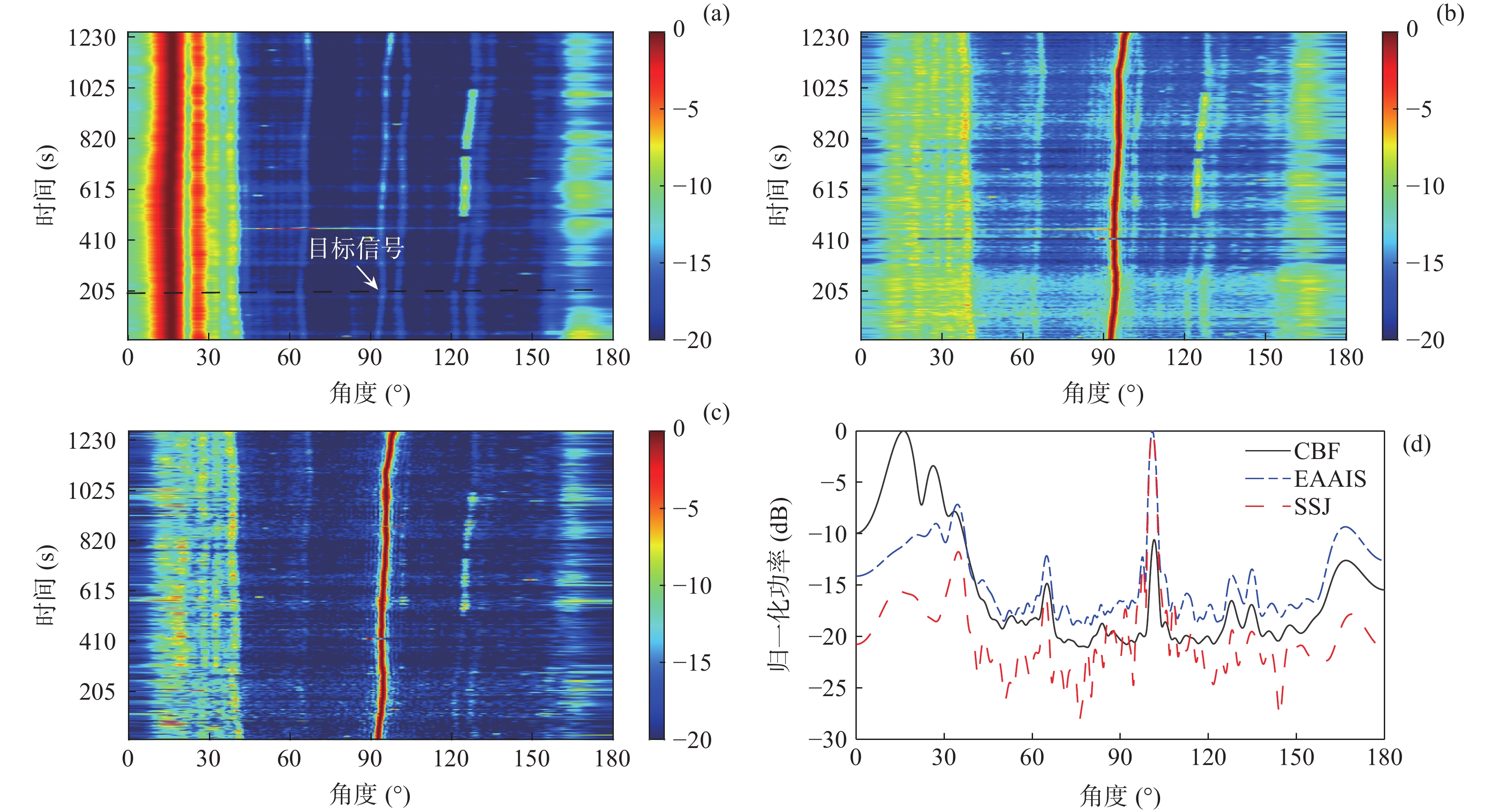
第1部分历程中, 目标信号功率较小, 并且端射方向的本舰干扰和其他方向的强干扰较多。图10(a)为经CBF处理后的时间方位历程图, 水下拖曳直线阵在拖曳过程中, 由于存在阵列端射方向的本舰干扰和其他方向的强干扰, CBF较难估计出目标角度信息。通过比较图10(a)和图10(b), 根据预估的目标角度区间, 可以发现EAAIS方法对目标角度变化具有较好的宽容性, 可稳健且自适应地抑制本舰干扰和其他方向的强干扰。其中, 本舰干扰的输出功率降低了约10 dB, 从而减小了强干扰的影响。然而, 由于宽带处理中EAAIS方法的阈值判决方式, 此方法并未有效地抑制干扰和噪声, 导致目标主瓣附近的旁瓣级较高。进一步对比图10(a)和图10(c), 可知SSJ方法中根据式(15)估计出的判决阈值
\eta = 0.28 \cdot N = 22.4 , 能够抑制大部分的干扰和噪声分量, 因而更加稳健地抑制端射方向的本舰干扰和其他方向的强干扰。其中, 本舰干扰的输出功率降低了约16 dB, 并且还降低了目标主瓣附近的旁瓣级, 准确估计出在强干扰环境下目标的角度信息, 验证了算法的可行性。从图10(d)中单个时间点处3种方法的归一化功率谱也可以看出, SSJ方法有效抑制了各个方向的强干扰, 降低了干扰的输出功率和目标主瓣附近的旁瓣级。第2部分历程中, 目标信号功率强度稍大, 端射方向的本舰干扰和其他方向的强干扰依然存在且数量较多, 功率也较强, 如图11(a)所示, CBF虽然可以分辨出目标, 但是强干扰的存在仍然影响目标的角度估计。通过对比经EAAIS干扰抑制后的时间方位历程(图11(b))和经SSJ干扰抑制后的时间方位历程(图11(c)), SSJ方法中同样根据式(15)估计的判决阈值
\eta = 0.45 \cdot N = 36 , 有效地抑制了端射方向和其他方向的强干扰。其中, 本舰干扰的输出功率降低了约15.5 dB, 而EAAIS方法抑制效果劣于SSJ方法, 本舰干扰的输出功率仅降低了约10 dB。因此, 在相同的场景中, SSJ方法具有更好的干扰抑制效果, 提高了目标方位角度的分辨力。从图11(d)中单个时间点处3种方法的归一化功率谱也可看出, SSJ方法更好地抑制了各个方向的强干扰, 具有更加稳健的干扰抑制能力。根据上述不同干扰抑制场景的海试数据处理结果分析得出, SSJ方法在存在本舰干扰等多个干扰的实际水声场景中, 依然能够稳健地抑制目标角度区间外的强干扰和噪声, 降低了干扰输出功率和目标主瓣附近的旁瓣级, 提高了目标方位角度的分辨力, 为后续的目标方位估计提供有效的处理手段。
5. 结论
在解决水下强干扰和环境噪声导致水下目标方位估计方法性能下降的问题方面, 本文所提子空间判决分析的干扰抑制方法具有良好的性能。该方法利用非目标子空间和导向矢量的正交性, 通过估计适当的判决阈值来识别和去除样本协方差矩阵中的非目标子空间, 从而稳健地抑制了强干扰和环境噪声, 降低了干扰的输出功率和目标主瓣附近的旁瓣级。仿真分析和海试数据处理结果都验证了SSJ方法对强干扰和噪声抑制的可行性。与文献中其他子空间干扰抑制方法相比, SSJ方法有效降低了本舰干扰的输出功率4 dB以上, 并且在目标主瓣附近的旁瓣级最大降低了10 dB, 具有更稳健的干扰抑制能力。此外, SSJ方法不需要计算所有方向区间内特征向量的空间功率谱估计的最大值, 计算效率更高。
由于SSJ方法粗估目标角度区间, 当目标和干扰出现交叉时, 性能可能会有所降低。目前的解决方法是通过不断缩小粗估的目标角度区间或动态调整阈值来分离干扰和噪声子空间。虽然SSJ方法提供了具体的判决阈值和判决比较的处理方式, 但判决阈值可能会受参数的影响而发生变化, 因此在复杂场景下实现自适应干扰抑制仍有一定的难度。为解决这个问题, 后续可考虑使用子空间匹配方法实现自适应的干扰抑制, 从而进一步提高SSJ方法的性能。
-
-
[1] Vaccaro R J, Chhetri A, Harrison B F. Matrix filter design for passive sonar interference suppression. J. Acoust. Soc. Am., 2004; 115(6): 3010—3020 DOI: 10.1121/1.1736653
[2] 鄢社锋, 侯朝焕, 马晓川. 矩阵空域预滤波目标方位估计. 声学学报, 2007; 32(2): 151—157 DOI: 10.3321/j.issn:0371-0025.2007.02.009 [3] 韩东, 章新华, 孙瑜. 宽带最优空域矩阵滤波器设计. 声学学报, 2011; 36(4): 405—411 DOI: 10.15949/j.cnki.0371-0025.2011.04.005 [4] Fan Z, Liang G, Wang Y, et al. Efficient Sub-Regional multiple-source detection based on subspace matrix filtering. IEEE Signal Process. Lett., 2014; 22(7): 943—947 DOI: 10.1109/LSP.2014.2379619
[5] 范展. 水下无人平台自主被动探测技术研究. 博士学位论文, 哈尔滨: 哈尔滨工程大学, 2015 [6] 梁国龙, 赵文彬, 付进. 一种降维空域滤波矩阵的设计方法. 电子学报, 2017; 45(2): 417—423 DOI: 10.3969/j.issn.0372-2112.2017.02.021 [7] Kirsteins I P, Tufts D W. Adaptive detection using low rank approximation to a data matrix. IEEE Trans. Aerosp. Electron. Syst., 1994; 30(1): 55—67 DOI: 10.1109/7.250406
[8] Harrison B F. The Eigen component association method for adaptive interference suppression. J. Acoust. Soc. Am., 2004; 115(5): 2122—2128 DOI: 10.1121/1.1699395
[9] 任岁玲, 葛凤翔, 郭良浩. 基于特征分析的自适应干扰抑制. 声学学报, 2013; 38(3): 272—280 DOI: 10.15949/j.cnki.0371-0025.2013.03.004 [10] Ren S, Ge F X, Guo X, et al. Eigenanalysis-Based adaptive interference suppression and its application in acoustic source range estimation. IEEE J. Oceanic Eng., 2015; 40(4): 903—916 DOI: 10.1109/JOE.2014.2359378
[11] Chen W, Zhang W, Wu Y, et al. Joint algorithm based on interference suppression and Kalman filter for bearing-only weak target robust tracking. IEEE Access, 2019; 7: 131653—131662 DOI: 10.1109/ACCESS.2019.2940956
[12] Sun D, Ma C, Yang T C, et al. Improving the performance of a vector sensor line array by deconvolution. IEEE J. Oceanic Eng., 2020; 45(3): 1063—1077 DOI: 10.1109/JOE.2019.2912586
[13] Park Y, Gerstoft P. Gridless sparse covariance-based beamforming via alternating projections including co-prime arrays. J. Acoust. Soc. Am., 2022; 151(6): 3828—3837 DOI: 10.1121/10.0011617
[14] 孙大军, 张珂, 梅继丹, 等. 稀疏矢量阵信号栅瓣及对称伪峰干扰抑制. 声学学报, 2021; 46(1): 23—34 DOI: 10.15949/j.cnki.0371-0025.2021.01.003 [15] 汪洋, 刘清宇, 段睿, 等. 波束形成后多干扰抵消方法. 声学学报, 2019; 44(4): 687—697 DOI: 10.15949/j.cnki.0371-0025.2019.04.029 [16] Nadakuditi R, Edelman A. Sample eigenvalue based detection of high-dimensional signals in white noise using relatively few samples. IEEE Trans. Signal Process., 2008; 56(7): 2625—2638 DOI: 10.1109/TSP.2008.917356
[17] Ollila E, Raninen E. Optimal shrinkage covariance matrix estimation under random sampling from elliptical distributions. IEEE Trans. Signal Process., 2019; 67(10): 2707—2719 DOI: 10.1109/TSP.2019.2908144
[18] Ollila E, Breloy A. Regularized tapered sample covariance matrix. IEEE Trans. Signal Process., 2022; 70: 2306—2320 DOI: 10.1109/TSP.2022.3169269
[19] Nadler B. Finite sample approximation results for principal component analysis: A matrix perturbation approach. Ann. Stat., 2008; 36(6): 2791—2817
[20] Johnstone L M, Lu A Y. On Consistency and sparsity for principal components analysis in high dimensions. J. Am. Stat. Assoc., 2009; 104(486): 682—693 DOI: 10.1198/jasa.2009.0121
[21] Wage K E, Buck J R. Snapshot performance of the dominant mode rejection beamformer. IEEE J. Oceanic Eng., 2014; 39(2): 212—225 DOI: 10.1109/JOE.2013.2251538
[22] Cox H. Resolving power and sensitivity to mismatch of optimum array processors. J. Acoust. Soc. Am., 1973; 54(3): 771—785 DOI: 10.1121/1.1913659



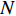
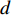
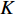
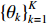
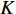
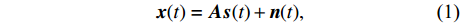
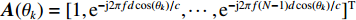
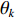
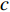
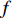
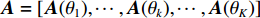
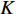
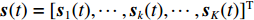
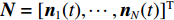

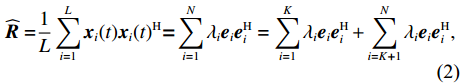
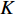
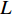
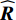

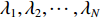
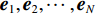
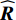
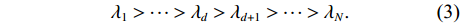
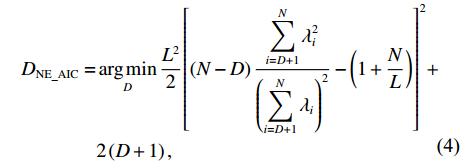

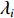
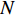

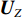
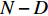
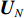
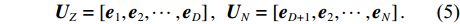

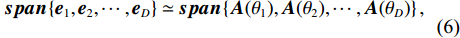
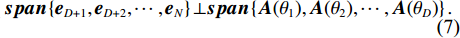
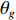
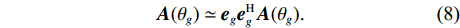
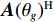
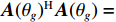
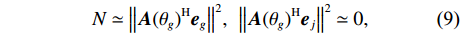

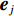
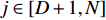
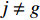
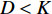
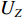
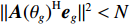
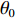
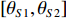
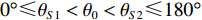
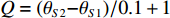

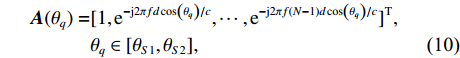
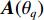
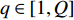
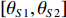
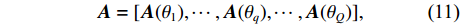
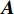



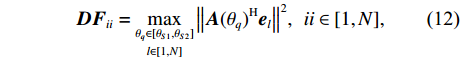
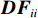

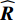
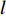

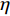
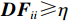
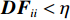
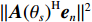
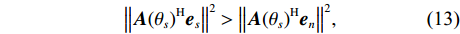
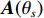
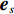
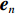
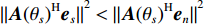
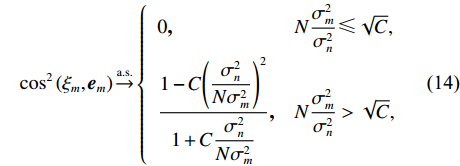
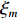
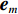
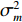
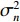

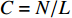
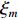
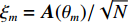
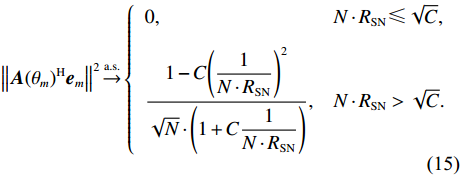
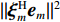
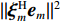
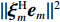
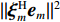
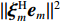
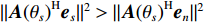
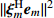
 下载:
下载: