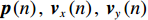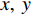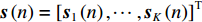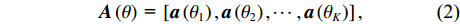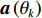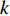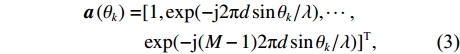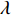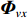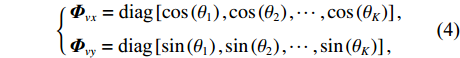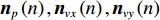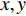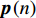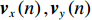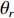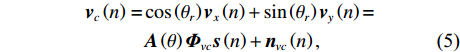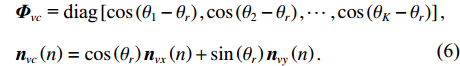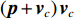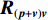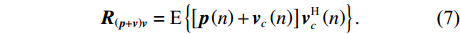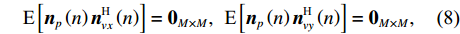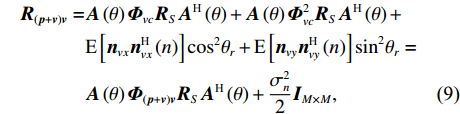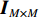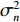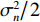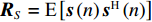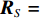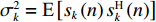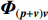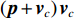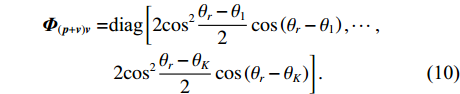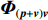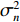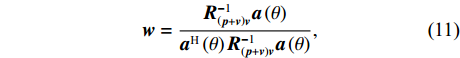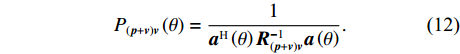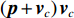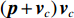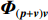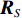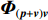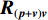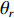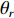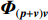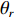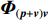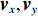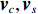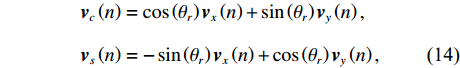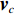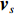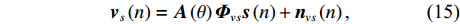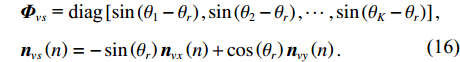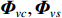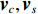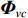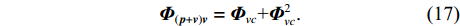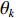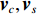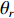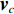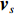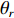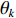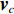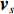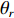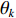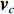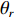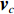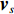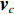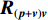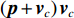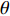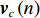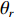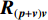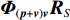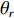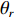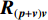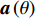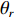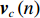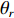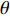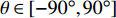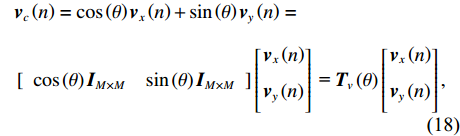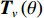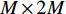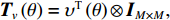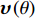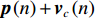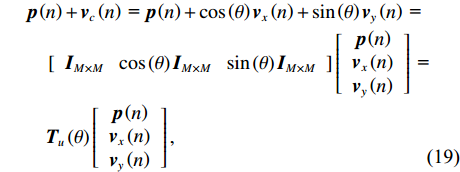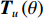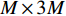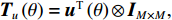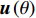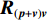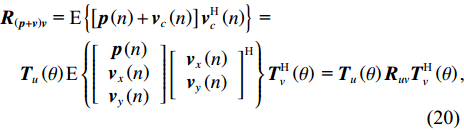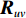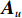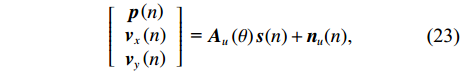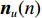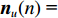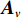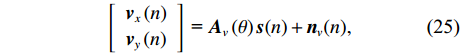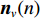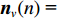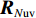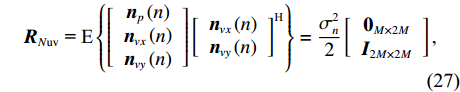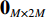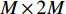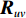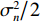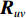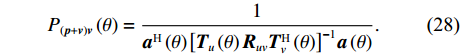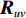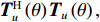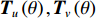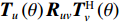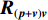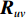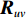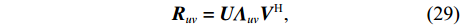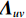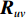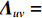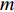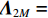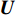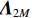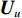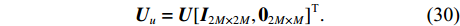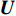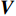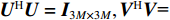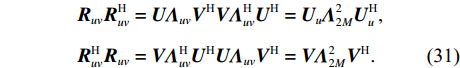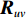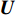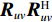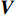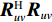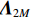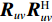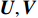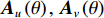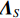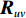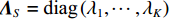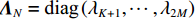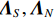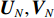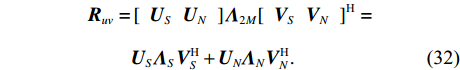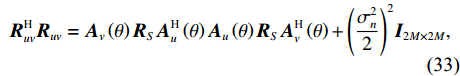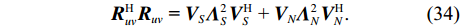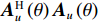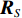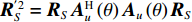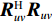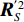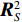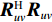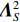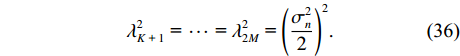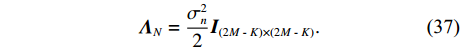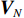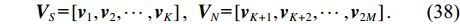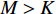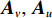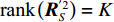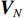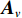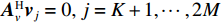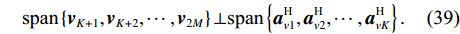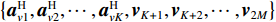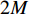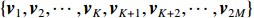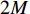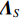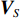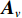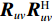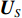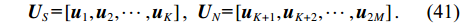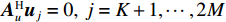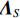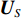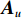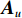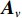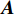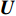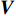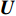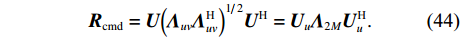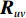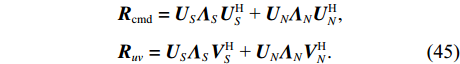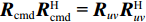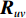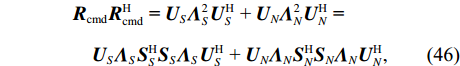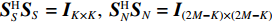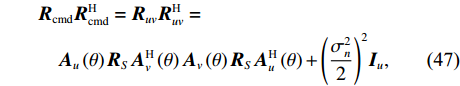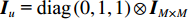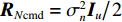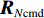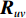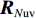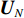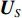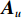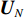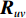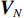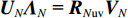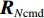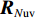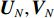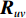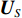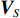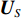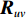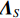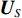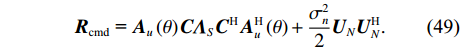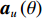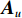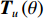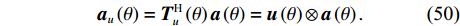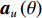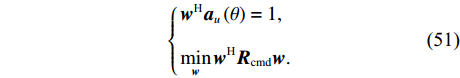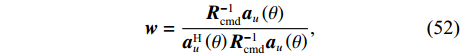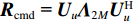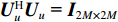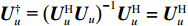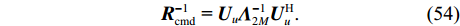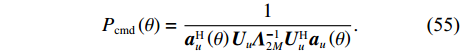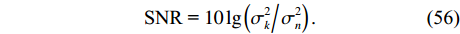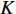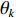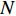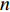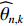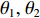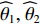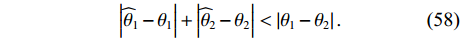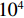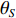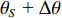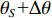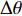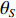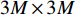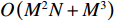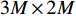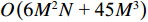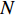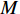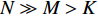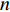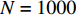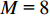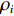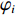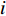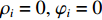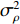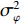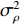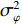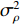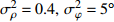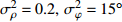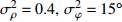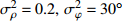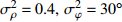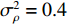Direction of arrival estimation of acoustic vector sensor array based on the combined information processing of pressure and particle velocity using covariance matrix decomposition
-
摘要:
提出一种使用协方差矩阵分解(CMD)的声矢量阵声压振速联合处理方法。该方法将声压振速互协方差矩阵分解为观测方位系数矩阵和剩余协方差矩阵, 将系数矩阵与导向矢量结合避免了观测方位的选择, 对剩余协方差矩阵进行奇异值分解并重构厄米特协方差矩阵, 最后对重构的协方差矩阵实施最小方差无失真响应(MVDR)方法处理。理论分析表明, 使用重构的协方差矩阵能够获得更高的阵处理增益。数值仿真结果验证了本文方法的计算量与Nehorai处理方法相近, 但较传统声压振速联合处理方法具有更高的阵处理增益和目标分辨能力。
Abstract:A combined processing method of pressure and particle velocity (PV-CPM) for acoustic vector sensor array using covariance matrix decomposition (CMD) is proposed. In this method, the cross-covariance matrix of pressure and particle velocity is decomposed into an observation angle coefficient matrix and a residual covariance matrix. To avoid choosing the observation angle, the coefficient matrix is combined with the guidance vector. By adopting the singular value decomposition, the residual covariance matrix is reconstructed into the new Hermitian covariance matrix, which is ultimately used to implement the MVDR beamforming method. Theoretical analysis shows that the new covariance matrix can achieve higher array processing gain. Furthermore, the numerical simulation proves that the computational complexity of the proposed method is similar to that of the Nehorai’s method, but its array processing gain and multi-target resolution are higher than those of the traditional PV-CPM.
-
引言
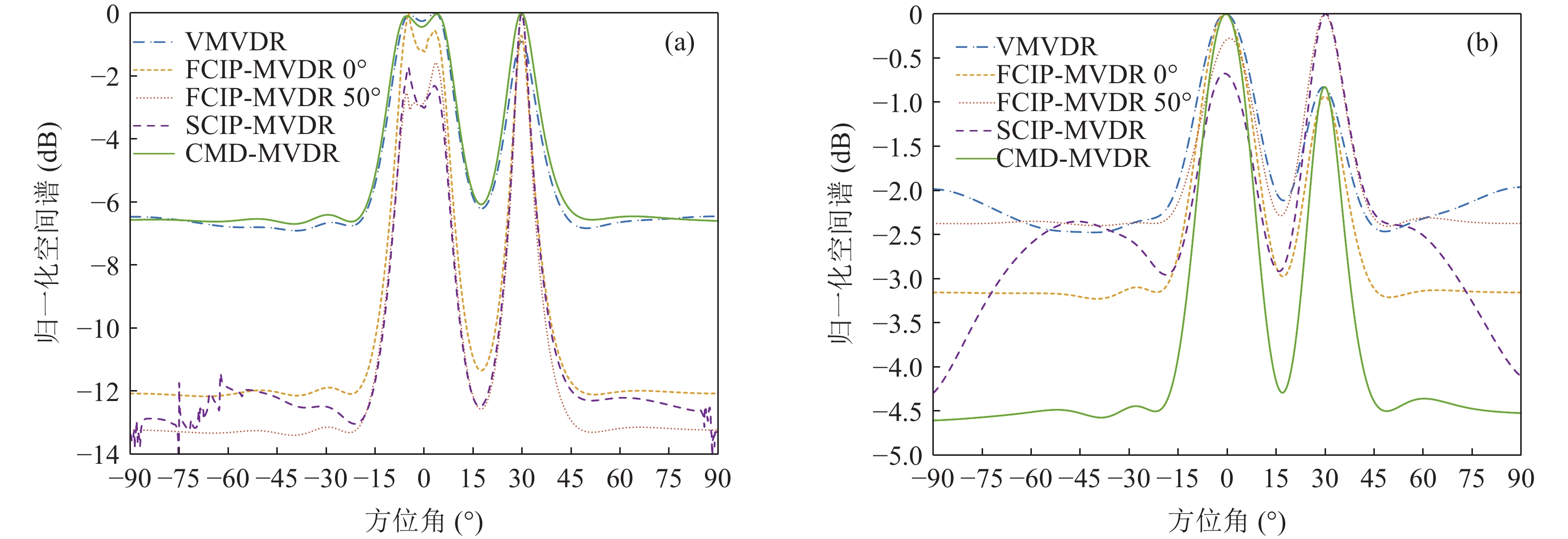
声矢量阵的波达方向(DOA)估计是水声阵列信号处理的热点问题[1-4]。由于感知声场信息更全面, 声矢量阵的信号处理方式更为多样化[5], 大体可分为基于Nehorai处理框架和声压振速联合处理两大类[6]。在Nehorai处理框架[7-8]中, 振速分量被视为独立的阵元信息, 与声压共同扩展构造成一个“长”的或“大”的阵列输出信号模型[9], 并基于该阵列信号模型的自协方差矩阵进行DOA估计, 但该方法没有充分利用声压振速相关性对各向同性噪声的抑制能力, 对DOA估计能力改善有限[10]。文献[11-12]研究结果表明, 各向同性噪声场的声压和振速分量之间是互不相关的, 这是声压振速联合处理的基础。而声压振速联合处理[10,13-16]则将振速分量投影到某观测方位上得到组合振速
{{\boldsymbol{v}}_c} , 并将声压{\boldsymbol{p}} 与组合振速{{\boldsymbol{v}}_c} 以特定方式组合构造互协方差矩阵, 常用组合方式有{\boldsymbol{p}}{{\boldsymbol{v}}_c} ,{\boldsymbol{p}} + {{\boldsymbol{v}}_c} ,{\boldsymbol{p}}\left( {{\boldsymbol{p}} + {{\boldsymbol{v}}_c}} \right) 和\left( {{\boldsymbol{p}} + {{\boldsymbol{v}}_c}} \right){{\boldsymbol{v}}_c} 等, 其中\left( {{\boldsymbol{p}} + {{\boldsymbol{v}}_c}} \right){{\boldsymbol{v}}_c} 具有最高的组合指向性增益[17], 可以很好地抑制各向同性噪声干扰, 且还具有抑制左右舷模糊能力。声矢量阵声压振速联合处理的关键问题是观测方位的选择, 通常可指定为某固定方向或随空间谱搜索方向扫描[10]。目前的研究大多采用固定观测方位的方式[10,13-15], 该方式具有处理简单、计算量小的优点, 但固定的观测方位决定了组合指向性的主极大方向[18], 会使指向性零点方向附近入射的信号被削弱或滤除。实际水声环境中, 目标的来向和数目都是无法预知的, 观测方位固定带来的空域滤波特性可能会导致方位估计性能下降或信源漏检等负面问题。文献[19]采用了随空间谱搜索扫描观测方位的方式, 避免了观测方位固定空间滤波造成的影响, 但由于该方式在每个观测方位的扫描点都必须重新构建声压振速互协方差矩阵, 使得算法的计算量剧烈增加, 难以满足水下目标探测的实时处理需求。
针对传统声压振速联合处理方法中观测方位选择的问题, 本文从理论上阐述了传统方法的DOA估计性能受观测方位影响的原因, 并提出一种基于协方差矩阵分解的声矢量阵声压振速联合处理MVDR方法。首先, 将声压振速互协方差矩阵分解为观测方位系数矩阵和剩余协方差矩阵, 系数矩阵直接与空间谱搜索的导向矢量结合, 避免了观测方位选择的问题。随后, 为保证协方差矩阵是方阵, 本文理论推导了剩余协方差矩阵奇异向量与导向矢量的对应关系, 通过奇异值分解完成了厄米特协方差矩阵的重构, 提高了阵处理增益。最后, 基于最小方差无失真响应(MVDR)波束形成器, 通过数值仿真比较了本文方法、Nehorai处理方法和传统声压振速联合处理方法的性能, 仿真结果验证了本文方法的性能优势。
1. 声矢量阵声压振速联合处理MVDR方法
1.1 声矢量阵输出信号模型
假设各向同性噪声场中, 存在
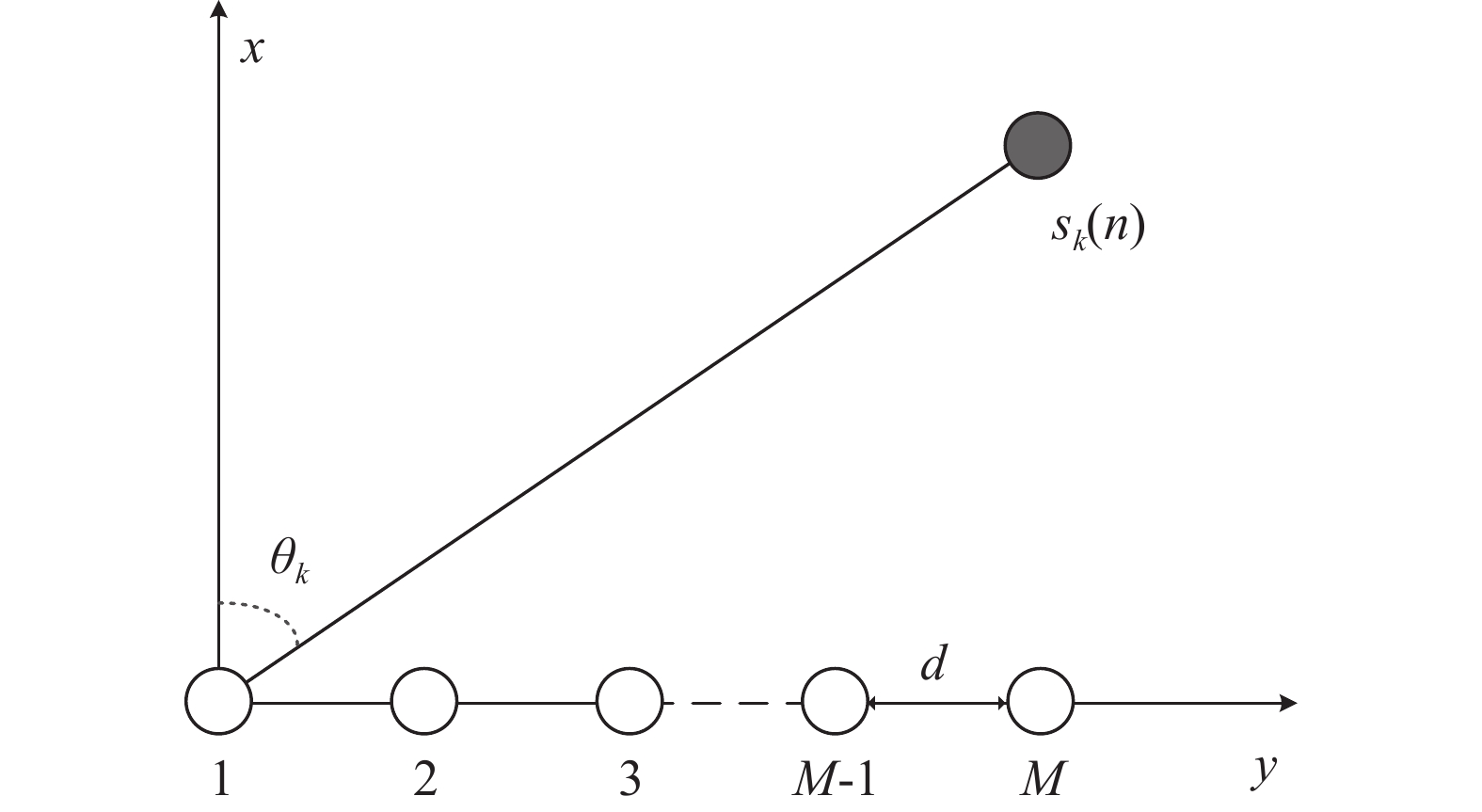
K 个独立的远场窄带信源入射到声矢量线列阵上, 阵列以首个阵元位置为参考点,M 个阵元沿y 轴正向等间隔布放, 相邻阵元间距为d 。入射角度为{\theta _k},{\text{ }}k = 1,2, \cdots ,K , 定义为信源与x 轴正向的夹角, 如图1所示。考虑远程探测情况, 不失一般性, 本文不考虑振速的
\textit z 分量, 那么, 矢量传感器阵列输出的快拍数据为\left\{ \begin{gathered} {\boldsymbol{p}}\left( n \right) = {\boldsymbol{A}}\left( \theta \right){\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_p}\left( n \right), \\ {{\boldsymbol{v}}_x}\left( n \right) = {\boldsymbol{A}}\left( \theta \right){{\boldsymbol{\varPhi }}_{vx}}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_{vx}}\left( n \right), \\ {{\boldsymbol{v}}_y}\left( n \right) = {\boldsymbol{A}}\left( \theta \right){{\boldsymbol{\varPhi }}_{vy}}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_{vy}}\left( n \right), \\ \end{gathered} \right. (1) 式中,
{\boldsymbol{p}}\left( n \right),{\text{ }}{{\boldsymbol{v}}_x}\left( n \right),{\text{ }}{{\boldsymbol{v}}_y}\left( n \right) 分别为声矢量阵列声压和振速x,{\text{ }}y 通道输出矢量,{\boldsymbol{s}}\left( n \right) = {\left[ {{{\boldsymbol{s}}_1}\left( n \right), \cdots ,{{\boldsymbol{s}}_K}\left( n \right)} \right]^{\text{T}}} 表示信源矢量;{\boldsymbol{A}}\left( \theta \right) 是声压传感器阵列流形矩阵, 有{\boldsymbol{A}}\left( \theta \right){\text{ = }}\left[ {{\boldsymbol{a}}\left( {{\theta _1}} \right),{\boldsymbol{a}}\left( {{\theta _2}} \right), \cdots ,{\boldsymbol{a}}\left( {{\theta _K}} \right)} \right], (2) {\boldsymbol{a}}\left( {{\theta _k}} \right) 为第k 个信源在声压传感器阵列上的导向矢量,\begin{split} {\boldsymbol{a}}\left( \theta _k \right) = & [ 1,\exp (-{\text{j}}2{\text{π}}d\sin\theta_k/\lambda), \cdots, \\& \exp (-{\text{j}}(M - 1)2{\text{π}}d\sin \theta_k/\lambda ) ]^{\text{T}}, \end{split} (3) 其中
\lambda 表示信源入射波长, 上标“{\text{T}} ”表示转置运算;{{\boldsymbol{\varPhi }}_{vx}} ,{{\boldsymbol{\varPhi }}_{vy}} 分别对应振速x,~y 通道输出的系数矩阵, 即\left\{ \begin{gathered} {{\boldsymbol{\varPhi }}_{vx}} = {\text{diag}}\left[ {\cos \left( {{\theta _1}} \right),\cos \left( {{\theta _2}} \right), \cdots ,\cos \left( {{\theta _K}} \right)} \right], \\ {{\boldsymbol{\varPhi }}_{vy}} = {\text{diag}}\left[ {\sin \left( {{\theta _1}} \right),\sin \left( {{\theta _2}} \right), \cdots ,\sin \left( {{\theta _K}} \right)} \right], \\ \end{gathered} \right. (4) {{\boldsymbol{n}}_p}\left( n \right),{{\boldsymbol{n}}_{vx}}\left( n \right),{{\boldsymbol{n}}_{vy}}\left( n \right) 分别为声矢量阵的声压和振速x,y 通道的噪声矢量, 假定阵列接收的噪声为零均值的高斯白噪声。1.2 声压振速联合处理MVDR方法
声压振速联合处理方法将声压
{\boldsymbol{p}}\left( n \right) 和振速分量{{\boldsymbol{v}}_x}\left( n \right),{{\boldsymbol{v}}_y}\left( n \right) 进行特定组合来构造互协方差矩阵。将式(1)中两振速分量{{\boldsymbol{v}}_x}\left( n \right),{{\boldsymbol{v}}_y}\left( n \right) 通过电子旋转投影到观测方位{\theta _r} 上, 获得组合振速:\begin{split} {{\boldsymbol{v}}_c}\left( n \right) = & \cos \left( {{\theta _r}} \right){{\boldsymbol{v}}_x}\left( n \right) + \sin \left( {{\theta _r}} \right){{\boldsymbol{v}}_y}\left( n \right) =\\& {\boldsymbol{A}}\left( \theta \right){{\boldsymbol{\varPhi }}_{vc}}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_{vc}}\left( n \right), \end{split} (5) 式中
\begin{split}& {{\boldsymbol{\varPhi }}_{vc}}{\text{ = diag}}\left[ {\cos \left( {{\theta _1} - {\theta _r}} \right),\cos \left( {{\theta _2} - {\theta _r}} \right), \cdots ,\cos \left( {{\theta _K} - {\theta _r}} \right)} \right], \\& {{\boldsymbol{n}}_{vc}}\left( n \right) = \cos \left( {{\theta _r}} \right){{\boldsymbol{n}}_{vx}}\left( n \right) + \sin \left( {{\theta _r}} \right){{\boldsymbol{n}}_{vy}}\left( n \right). \\[-12pt] \end{split} (6) 若采用
\left( {{\boldsymbol{p}} + {{\boldsymbol{v}}_c}} \right){{\boldsymbol{v}}_c} 组合形式构造声压振速互协方差矩阵{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} , 则其可表示为{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = {\text{E}}\left\{ {\left[ {{\boldsymbol{p}}\left( n \right) + {{\boldsymbol{v}}_c}\left( n \right)} \right]{\boldsymbol{v}}_c^{\text{H}}\left( n \right)} \right\}. (7) 文献[11]指出, 各向同性噪声场中, 噪声的声压分量和振速分量可以视为不相关, 所以
{\text{E}}\left[ {{{\boldsymbol{n}}_p}\left( n \right){\boldsymbol{n}}_{vx}^{\text{H}}\left( n \right)} \right] = {{\boldsymbol{0}}_{M \times M}},\;\;{\text{E}}\left[ {{{\boldsymbol{n}}_p}\left( n \right){\boldsymbol{n}}_{vy}^{\text{H}}\left( n \right)} \right] = {{\boldsymbol{0}}_{M \times M}}, (8) 式中,
{{\boldsymbol{0}}_{M \times M}} 为M \times M 维零矩阵。那么, 将式(1)和式(5)代入式(7), 可化简为\begin{split} {{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = &{\boldsymbol{A}}\left( \theta \right){{\boldsymbol{\varPhi }}_{vc}}{{\boldsymbol{R}}_S}{{\boldsymbol{A}}^{\text{H}}}\left( \theta \right) + {\boldsymbol{A}}\left( \theta \right){\boldsymbol{\varPhi }}_{vc}^2{{\boldsymbol{R}}_S}{{\boldsymbol{A}}^{\text{H}}}\left( \theta \right)+ \\ & {\text{E}}\left[ {{{\boldsymbol{n}}_{vx}}{\boldsymbol{n}}_{vx}^{\text{H}}\left( n \right)} \right]{\cos ^2}{\theta _r} + {\text{E}}\left[ {{{\boldsymbol{n}}_{vy}}{\boldsymbol{n}}_{vy}^{\text{H}}\left( n \right)} \right]{\sin ^2}{\theta _r}= \\ & {\boldsymbol{A}}\left( \theta \right){{\boldsymbol{\varPhi }}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{{\boldsymbol{R}}_S}{{\boldsymbol{A}}^{\text{H}}}\left( \theta \right) + \frac{{\sigma _n^2}}{2}{{\boldsymbol{I}}_{M \times M}}, \end{split} (9) 式中,
{{\boldsymbol{I}}_{M \times M}} 为M \times M 维单位阵,\sigma _n^2 为声压通道的噪声功率, 则振速通道噪声功率为{{\sigma _n^2} \mathord{\left/ {\vphantom {{\sigma _n^2} 2}} \right. } 2} , 信号协方差矩阵{{\boldsymbol{R}}_S} = {\text{E}}\left[ {{\boldsymbol{s}}\left( n \right){{\boldsymbol{s}}^{\text{H}}}\left( n \right)} \right] , 由于各信源相互独立, 则{{\boldsymbol{R}}_S} = {\text{diag}}\left[ {\sigma _1^2, \cdots ,\sigma _k^2} \right] ,\sigma _k^2 = {\text{E}}\left[ {{s_k}\left( n \right)s_k^{\text{H}}\left( n \right)} \right] 为第k 个入射信号功率,{{\boldsymbol{\varPhi }}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 为\left( {{\boldsymbol{p}} + {{\boldsymbol{v}}_c}} \right){{\boldsymbol{v}}_c} 互协方差加权系数矩阵:\begin{split} {{\boldsymbol{\varPhi }}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}=&{\text{diag}}\left[ 2{{\cos }^2}\frac{{{\theta _r} - {\theta _1}}}{2}\cos \left( {{\theta _r} - {\theta _1}} \right), \cdots ,\right.\\&\left.2{{\cos }^2}\frac{{{\theta _r} - {\theta _K}}}{2}\cos \left( {{\theta _r} - {\theta _K}} \right) \right]. \end{split} (10) 式(9)中第1项为信号部分, 通过
{{\boldsymbol{\varPhi }}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 包含的\left( {{\boldsymbol{p}} + {{\boldsymbol{v}}_c}} \right){{\boldsymbol{v}}_c} 组合指向性获得指向性增益, 第2项为噪声部分, 由于声场声压振速的空间相关特性, 其噪声功率降为声压通道噪声功率\sigma _n^2 的一半。MVDR方法在保证波达方向输出能量不变的前提下, 使其他方向的信号或干扰能量最小化, 该方法通过波束扫描获得空间谱, 以空间谱搜索范围内的谱峰确定不同方向的信源。对协方差矩阵
{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 实施MVDR处理, 则可得基于声压振速联合处理MVDR方法的最优权矢量:{\boldsymbol{w}} = \frac{{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{ - 1}{\boldsymbol{a}}\left( \theta \right)}}{{{{\boldsymbol{a}}^{\text{H}}}\left( \theta \right){\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{ - 1}{\boldsymbol{a}}\left( \theta \right)}}, (11) 通过波束扫描获得的空间谱为
{P_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}\left( \theta \right) = \frac{1}{{{{\boldsymbol{a}}^{\text{H}}}\left( \theta \right){\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{ - 1}{\boldsymbol{a}}\left( \theta \right)}}. (12) 1.3 已有处理方法的问题分析
声压振速联合处理MVDR算法性能的提升, 是
\left( {{\boldsymbol{p}} + {{\boldsymbol{v}}_c}} \right){{\boldsymbol{v}}_c} 指向性增益和声压振速空间相关特性的共同作用。\left({\boldsymbol{p}}+{\boldsymbol{v}}_c\right) {\boldsymbol{v}}_c 的指向性是由\boldsymbol{\varPhi}_{({\boldsymbol{p}}+{\boldsymbol{v}}) {\boldsymbol{v}}} 对信号协方差矩阵{\boldsymbol{R}}_S 加权得到的, 由于\boldsymbol{\varPhi}_{({\boldsymbol{p}}+{\boldsymbol{v}}) {\boldsymbol{v}}} 包含方位信息, 实际等效为对{\boldsymbol{R}}_S 做空间滤波处理, 那么\boldsymbol{R}_{({\boldsymbol{p}}+{\boldsymbol{v}}) {\boldsymbol{v}}} 中信号部分:\begin{split} {{\boldsymbol{\varPhi }}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{{\boldsymbol{R}}_S} =& {\text{diag}}\left[ 2\sigma _1^2{\text{co}}{{\text{s}}^2}\frac{{{\theta _1} - {\theta _r}}}{2}\cos \left( {{\theta _1} - {\theta _r}} \right), \cdots ,\right.\\&\left.2\sigma _K^2{\text{co}}{{\text{s}}^2}\frac{{{\theta _K} - {\theta _r}}}{2}\cos \left( {{\theta _K} - {\theta _r}} \right) \right]. \end{split} (13) 当观测方位
{\theta _r} 指定为某固定值时, 若{\theta _r} 选择适当,\boldsymbol{\varPhi}_{({\boldsymbol{p}}+{\boldsymbol{v}}) {\boldsymbol{v}}} 能够放大信号功率, 使信噪比得到改善。但是, 若{\theta _r} 与波达方向偏离过大, 特别是与波达方向垂直时,\boldsymbol{\varPhi}_{({\boldsymbol{p}}+{\boldsymbol{v}}) {\boldsymbol{v}}} 带来的空间滤波能力可能使该方向信号被削弱或滤除, 进而导致DOA性能下降或信源漏检。上述问题也可以从电子旋转的角度来解释。矢量传感器输出的
{{\boldsymbol{v}}_x},{{\boldsymbol{v}}_y} 是两正交的振速分量, 经电子旋转后, 可以获得一组同样正交的振速分量{{\boldsymbol{v}}_c},{{\boldsymbol{v}}_s} , 即\begin{split}& {{\boldsymbol{v}}_c}\left( n \right) = \cos \left( {{\theta _r}} \right){{\boldsymbol{v}}_x}\left( n \right) + \sin \left( {{\theta _r}} \right){{\boldsymbol{v}}_y}\left( n \right), \\& {{\boldsymbol{v}}_s}\left( n \right) = - \sin \left( {{\theta _r}} \right){{\boldsymbol{v}}_x}\left( n \right) + \cos \left( {{\theta _r}} \right){{\boldsymbol{v}}_y}\left( n \right), \end{split} (14) 式中,
{{\boldsymbol{v}}_c} 为声压振速联合处理选取的组合振速, 与式(5)类似,{{\boldsymbol{v}}_s} 可化简为{{\boldsymbol{v}}_s}\left( n \right) = {\boldsymbol{A}}\left( \theta \right){{\boldsymbol{\varPhi }}_{vs}}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_{vs}}\left( n \right), (15) 式中
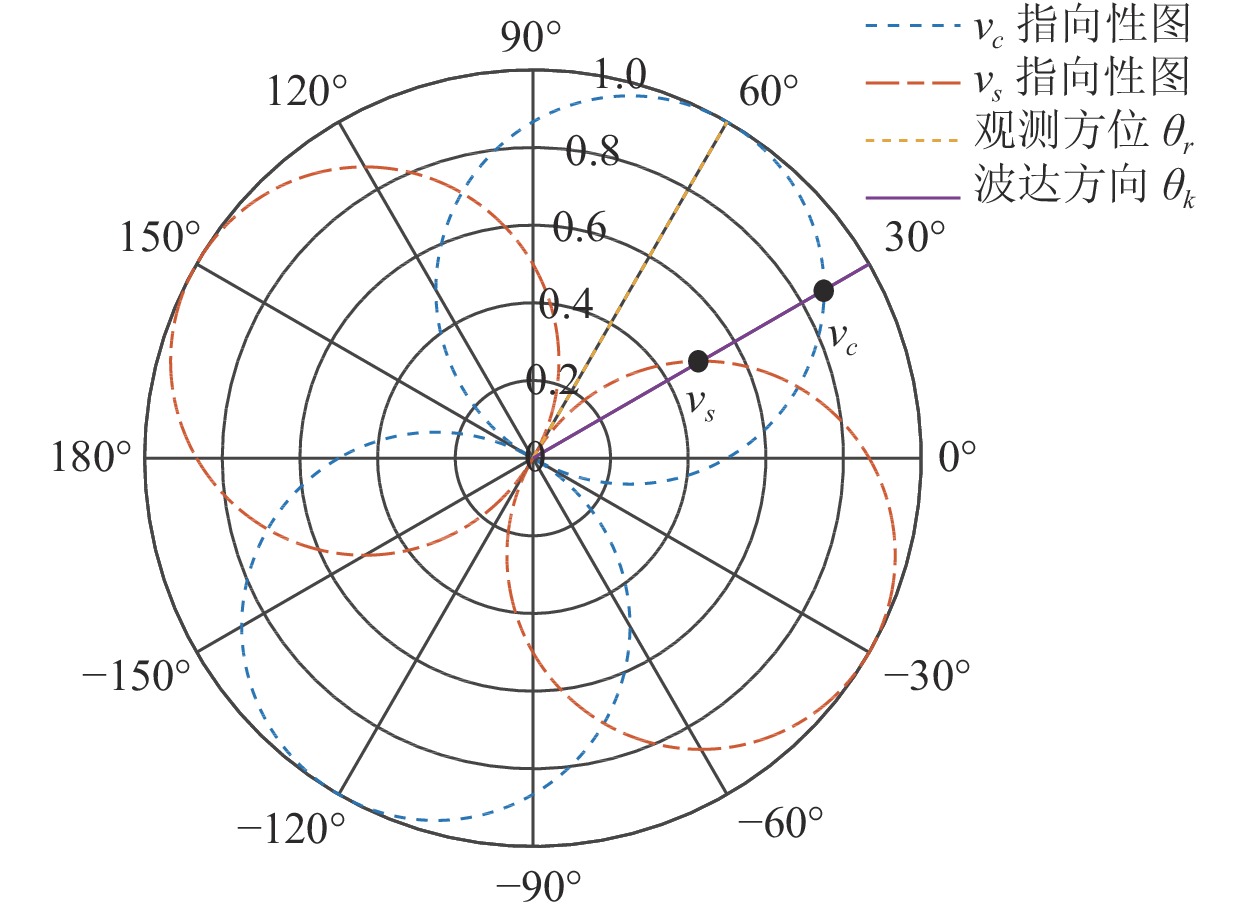
\begin{split}& {{\boldsymbol{\varPhi }}_{vs}}{\text{ = diag}}\left[ {\sin \left( {{\theta _1} - {\theta _r}} \right),\sin \left( {{\theta _2} - {\theta _r}} \right), \cdots ,\sin \left( {{\theta _K} - {\theta _r}} \right)} \right], \\& {{\boldsymbol{n}}_{vs}}\left( n \right) = - \sin \left( {{\theta _r}} \right){{\boldsymbol{n}}_{vx}}\left( n \right) + \cos \left( {{\theta _r}} \right){{\boldsymbol{n}}_{vy}}\left( n \right). \\[-12pt] \end{split} (16) \boldsymbol{\varPhi}_{v c}, \boldsymbol{\varPhi}_{v s} 分别包含{{\boldsymbol{v}}_c},{{\boldsymbol{v}}_s} 的指向性信息, 传统声压振速联合处理仅利用\boldsymbol{\varPhi}_{v c} 获得组合指向性:{{\boldsymbol{\varPhi }}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = {{\boldsymbol{\varPhi }}_{vc}}{\text{+}}{\boldsymbol{\varPhi }}_{vc}^2. (17) 当存在波达方向
{\theta _k} 的信源入射时, 通过设定观测方位{\theta _r} 可分别获得{\boldsymbol{v}}_c, {\boldsymbol{v}}_s 分量信息, 如图2所示, 观测方位{\theta _r} 对应{{\boldsymbol{v}}_c} 的主极大方向, 即{\boldsymbol{v}}_s 的指向性零点方向。那么, 当观测方位{\theta _r} 与波达方向{\theta _k} 一致时, 信号功率完全集中在{{\boldsymbol{v}}_c} 方向上,{{\boldsymbol{v}}_s} 分量为0。随着观测方位{\theta _r} 偏离波达方向{\theta _k} ,{{\boldsymbol{v}}_c} 分量逐渐减小,{{\boldsymbol{v}}_s} 分量逐渐增大却未被利用, 导致信号功率损失, 特别是当观测方位{\theta _r} 与波达方向{\theta _k} 垂直时, 信号功率的损失达到最大。当观测方位
{\theta _r} 随空间谱搜索方向扫描时, 因空域滤波特性导致信号被削弱或滤除的问题得以解决。此时,{{\boldsymbol{v}}_c} 的主极大方向将始终指向预设波达方向,{{\boldsymbol{v}}_s} 分量始终为零。但是,{{\boldsymbol{v}}_c} 随谱搜索方位变化导致声压振速互协方差矩阵{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 也随之变化。这使得算法计算复杂度剧烈增加, 特别是MVDR算法需要对协方差矩阵进行取逆运算, 更是降低了处理器的效率, 不利于阵列信号的实时处理。2. 基于协方差矩阵分解的声矢量阵MVDR方法
2.1 观测方位的提取
\left({\boldsymbol{p}} + {\boldsymbol{v}}_c\right) {\boldsymbol{v}}_c 声压振速联合处理中, 如果使观测方位\theta_r 随空间谱搜索方位\theta 扫描, 算法复杂度会剧烈增加。这是由于组合振速{{\boldsymbol{v}}_c}\left( n \right) 中同时涵盖了波达方向{\theta _k} 和观测方位{\theta _r} , 导致{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 的信号部分{{\boldsymbol{\varPhi }}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{{\boldsymbol{R}}_S} 与观测方位{\theta _r} 有关, 若将观测方位{\theta _r} 从{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 中剥离, 将其与空间谱搜索的导向矢量{\boldsymbol{a}}\left( \theta \right) 结合, 以使观测方位{\theta _r} 始终指向预设波达方向, 这样既保证了无信号功率损失, 而且无需重复计算协方差矩阵。重写组合振速
{{\boldsymbol{v}}_c}\left( n \right) 的表达式, 设置观测方位{\theta _r} 为空间谱搜索方位\theta , 且\theta \in \left[ { - {{90}\text{°} },{{90}\text{°}}} \right] , 则式(5)可表示为\begin{split}& {{\boldsymbol{v}}_c}\left( n \right) = \cos \left( \theta \right){{\boldsymbol{v}}_x}\left( n \right) + \sin \left( \theta \right){{\boldsymbol{v}}_y}\left( n \right) = \\& \left[ {\begin{array}{*{20}{c}} {\cos \left( \theta \right){{\boldsymbol{I}}_{M \times M}}}&{\sin \left( \theta \right){{\boldsymbol{I}}_{M \times M}}} \end{array}} \right]\left[ \begin{gathered} {{\boldsymbol{v}}_x}\left( n \right) \\ {{\boldsymbol{v}}_y}\left( n \right) \\ \end{gathered} \right]{\text{ = }}{{\boldsymbol{T}}_v}\left( \theta \right)\left[ \begin{gathered} {{\boldsymbol{v}}_x}\left( n \right) \\ {{\boldsymbol{v}}_y}\left( n \right) \\ \end{gathered} \right], \end{split} (18) 式中,
{{\boldsymbol{T}}_v}\left( \theta \right) 是M \times 2M 维矩阵,{{\boldsymbol{T}}}_{v}\left(\theta \right)={\upsilon }^{\text{T}}\left(\theta \right)\otimes {{\boldsymbol{I}}}_{M\times M }, {\boldsymbol{\upsilon}} \left(\theta \right)\text{=}{\left[\mathrm{cos}\left(\theta \right), \mathrm{sin}\left(\theta \right)\right]}^{\text{T}} ,{\boldsymbol{\upsilon }}\left( \theta \right) 是单振速传感器的阵列流形。同理,{\boldsymbol{p}}\left( n \right) + {{\boldsymbol{v}}_c}\left( n \right) 可表示为\begin{split}& {\boldsymbol{p}}\left( n \right) + {{\boldsymbol{v}}_c}\left( n \right){\text{ = }}{\boldsymbol{p}}\left( n \right) + \cos \left( \theta \right){{\boldsymbol{v}}_x}\left( n \right) + \sin \left( \theta \right){{\boldsymbol{v}}_y}\left( n \right) {\text{ = }} \\&\quad \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{I}}_{M \times M}}}~~~ {\cos \left( \theta \right){{\boldsymbol{I}}_{M \times M}}}~~~ {\sin \left( \theta \right){{\boldsymbol{I}}_{M \times M}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{p}}\left( n \right)} \\ {{{\boldsymbol{v}}_x}\left( n \right)} \\ {{{\boldsymbol{v}}_y}\left( n \right)} \end{array}} \right]{\text{ = }}\\&\quad{{\boldsymbol{T}}_u}\left( \theta \right)\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{p}}\left( n \right)} \\ {{{\boldsymbol{v}}_x}\left( n \right)} \\ {{{\boldsymbol{v}}_y}\left( n \right)} \end{array}} \right],\\[-12pt] \end{split} (19) 式中,
{{\boldsymbol{T}}_u}\left( \theta \right) 是M \times 3M 维矩阵,{{\boldsymbol{T}}}_{u}\left(\theta \right)={{\boldsymbol{u}}}^{\text{T}}\left(\theta \right)\otimes {{\boldsymbol{I}}}_{M\times M}, {\boldsymbol{u}}\left(\theta \right)\text{=}{\left[1,\mathrm{cos}\left(\theta \right), \mathrm{sin}\left(\theta \right)\right]}^{\text{T}} ,{\boldsymbol{u}}\left( \theta \right) 是单矢量传感器的阵列流形。将式(18)和式(19)代入式(7), 则{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 可分解为观测方位系数矩阵与协方差矩阵相乘的形式:\begin{split}& {{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{\text{ = E}}\left\{ {\left[ {{\boldsymbol{p}}\left( n \right) + {{\boldsymbol{v}}_c}\left( n \right)} \right]{\boldsymbol{v}}_c^{\text{H}}\left( n \right)} \right\} {\text{ = }}\\&\quad {{\boldsymbol{T}}_u}\left( \theta \right){\text{E}}\left\{ {\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{p}}\left( n \right)} \\ {{{\boldsymbol{v}}_x}\left( n \right)} \\ {{{\boldsymbol{v}}_y}\left( n \right)} \end{array}} \right]{{\left[ \begin{array}{*{20}{c}} {{\boldsymbol{v}}_x}\left( n \right) \\ {{\boldsymbol{v}}_y}\left( n \right) \\ \end{array} \right]}^{\text{H}}}} \right\}{\boldsymbol{T}}_v^{\text{H}}\left( \theta \right){\text{ = }}{{\boldsymbol{T}}_u}\left( \theta \right){{\boldsymbol{R}}_{uv}}{\boldsymbol{T}}_v^{\text{H}}\left( \theta \right), \end{split} (20) 式中,
{{\boldsymbol{R}}_{uv}} 为由声压和振速经特定组合而成的剩余协方差矩阵,{{\boldsymbol{R}}_{uv}}{\text{ = E}}\left\{ {\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{p}}\left( n \right)} \\ {{{\boldsymbol{v}}_x}\left( n \right)} \\ {{{\boldsymbol{v}}_y}\left( n \right)} \end{array}} \right]{{\left[ \begin{array}{*{20}{c}} {{\boldsymbol{v}}_x}\left( n \right) \\ {{\boldsymbol{v}}_y}\left( n \right) \\ \end{array} \right]}^{\text{H}}}} \right\}. (21) 定义
{{\boldsymbol{A}}_u} 为声矢量传感器的阵列流形矩阵,\begin{array}{l}{{\boldsymbol{A}}_u}{\text{ = }}\left[ {{\boldsymbol{u}}\left( {{\theta _1}} \right) \otimes {\boldsymbol{a}}\left( {{\theta _1}} \right), \cdots ,{\boldsymbol{u}}\left( {{\theta _K}} \right) \otimes {\boldsymbol{a}}\left( {{\theta _K}} \right)} \right]{\text{ = }}\left[ {{{\boldsymbol{a}}_{u1}}, \cdots ,{{\boldsymbol{a}}_{uK}}} \right],\\[2mm] \end{array} (22) 则有
\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{p}}\left( n \right)} \\ {{{\boldsymbol{v}}_x}\left( n \right)} \\ {{{\boldsymbol{v}}_y}\left( n \right)} \end{array}} \right]{\text{ = }}{{\boldsymbol{A}}_u}\left( \theta \right){\boldsymbol{s}}(n) + {{\boldsymbol{n}}_u}(n), (23) 式中,
{{\boldsymbol{n}}_u}(n) 为声矢量阵的背景噪声矢量,{{\boldsymbol{n}}_u}(n){\text{ = }} {\left[ {{\boldsymbol{n}}_p^{\text{T}}(n),{\boldsymbol{n}}_{vx}^{\text{T}}(n),{\boldsymbol{n}}_{vy}^{\text{T}}(n)} \right]^{\text{T}}} 。类似地, 定义{{\boldsymbol{A}}_v} 是振速传感器阵列流形矩阵,\begin{array}{l}{{\boldsymbol{A}}_v}{\text{ = }}\left[ {{\boldsymbol{v}}\left( {{\theta _1}} \right) \otimes {\boldsymbol{a}}\left( {{\theta _1}} \right), \cdots ,{\boldsymbol{v}}\left( {{\theta _K}} \right) \otimes {\boldsymbol{a}}\left( {{\theta _K}} \right)} \right]{\text{ = }}\left[ {{{\boldsymbol{a}}_{v1}}, \cdots ,{{\boldsymbol{a}}_{vK}}} \right],\\[2mm] \end{array} (24) 则有
\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{v}}_x}\left( n \right)} \\ {{{\boldsymbol{v}}_y}\left( n \right)} \end{array}} \right]{\text{ = }}{{\boldsymbol{A}}_v}\left( \theta \right){\boldsymbol{s}}(n) + {{\boldsymbol{n}}_v}(n), (25) 式中,
{{\boldsymbol{n}}_v}(n) 为振速传感器阵列的背景噪声矢量,{{\boldsymbol{n}}_v}(n){\text{ = }} {\left[ {{\boldsymbol{n}}_{vx}^{\text{T}}(n),{\boldsymbol{n}}_{vy}^{\text{T}}(n)} \right]^{\text{T}}} 。将式(23)和式(25)代入式(20), 可重写为\begin{split} {{\boldsymbol{R}}_{uv}}=& {\text{E}}\left\{ {\left[ {{{\boldsymbol{A}}_u}\left( \theta \right){\boldsymbol{s}}(n) + {{\boldsymbol{n}}_u}(n)} \right]{{\left[ {{{\boldsymbol{A}}_v}\left( \theta \right){\boldsymbol{s}}(n) + {{\boldsymbol{n}}_v}(n)} \right]}^{\text{H}}}} \right\} = \\& {\text{E}}\left[ {{{\boldsymbol{A}}_u}\left( \theta \right){\boldsymbol{s}}(n){{\boldsymbol{s}}^{\text{H}}}(n){\boldsymbol{A}}_v^{\text{H}}\left( \theta \right)} \right] + {\text{E}}\left[ {{{\boldsymbol{n}}_u}(n){\boldsymbol{n}}_v^{\text{H}}(n)} \right] = \\& {{\boldsymbol{A}}_u}\left( \theta \right){{\boldsymbol{R}}_S}{\boldsymbol{A}}_v^{\text{H}}\left( \theta \right) + {{\boldsymbol{R}}_{N{\rm uv}}}, \\[-12pt] \end{split} (26) 式中,
{{\boldsymbol{R}}_{N{\rm uv}}} 是剩余噪声协方差矩阵,{{\boldsymbol{R}}_{N{\rm uv}}}{\text{ = E}}\left\{ {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{n}}_p}\left( n \right)} \\ {{{\boldsymbol{n}}_{vx}}\left( n \right)} \\ {{{\boldsymbol{n}}_{vy}}\left( n \right)} \end{array}} \right]{{\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{n}}_{vx}}\left( n \right)} \\ {{{\boldsymbol{n}}_{vy}}\left( n \right)} \end{array}} \right]}^{\text{H}}}} \right\} = \frac{{\sigma _n^2}}{2}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{0}}_{M \times 2M}}} \\ {{{\boldsymbol{I}}_{2M \times 2M}}} \end{array}} \right], (27) 式中,
{{\boldsymbol{0}}_{M \times 2M}} 是M \times 2M 维零矩阵,{{\boldsymbol{I}}_{2M \times 2M}} 是2M \times 2M 维单位阵。可见,
{{\boldsymbol{R}}_{uv}} 中同样包含信号功率与波达方向信息, 且协方差矩阵中仅含振速通道噪声功率{{\sigma _n^2} \mathord{\left/ {\vphantom {{\sigma _n^2} 2}} \right. } 2} 。那么, 可以选用{{\boldsymbol{R}}_{uv}} 作为协方差矩阵进行方位估计。将式(20)代入式(12), 可得MVDR空间谱表达式:{P_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}\left( \theta \right) = \frac{1}{{{{\boldsymbol{a}}^{\text{H}}}\left( \theta \right){{\left[ {{{\boldsymbol{T}}_u}\left( \theta \right){{\boldsymbol{R}}_{uv}}{\boldsymbol{T}}_v^{\text{H}}\left( \theta \right)} \right]}^{ - 1}}{\boldsymbol{a}}\left( \theta \right)}}. (28) 由式(28)可以发现, 由于协方差矩阵
{{\boldsymbol{R}}_{uv}} 为3M \times 2M 维矩阵, 不是厄米特矩阵, 而且{\boldsymbol{T}}_u^{\text{H}}\left( \theta \right){{\boldsymbol{T}}_u}\left( \theta \right), {\boldsymbol{T}}_v^{\text{H}}\left( \theta \right){{\boldsymbol{T}}_v}\left( \theta \right) 均为奇异矩阵, 即{{\boldsymbol{T}}_u}\left( \theta \right),{{\boldsymbol{T}}_v}\left( \theta \right) 不存在广义逆, 所以无法直接利用{{\boldsymbol{T}}_u}\left( \theta \right){{\boldsymbol{R}}_{uv}}{\boldsymbol{T}}_v^{\text{H}}\left( \theta \right) 替代{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 求逆, 还需对{{\boldsymbol{R}}_{uv}} 做进一步修正。2.2 协方差矩阵的分解与重构
在空间谱估计中, 协方差矩阵经特征分解后, 较大特征值对应的特征向量与入射信号导向矢量张成的空间相同[20], 因此可以利用特征值与特征向量对协方差矩阵进行重构。但是, 特征分解通常只适用于方阵, 对于非方阵可以使用奇异值分解, 那么协方差矩阵
{{\boldsymbol{R}}_{uv}} 可表示为{{\boldsymbol{R}}_{uv}} = {\boldsymbol{U}}{{\boldsymbol{\varLambda }}_{uv}}{{\boldsymbol{V}}^{\text{H}}}, (29) 式中,
{{\boldsymbol{\varLambda }}_{uv}} 是{{\boldsymbol{R}}_{uv}} 的奇异值矩阵, 可以写作{{\boldsymbol{\varLambda }}_{uv}} = {\left[ {{{\boldsymbol{\varLambda }}_{2M}},{{\boldsymbol{0}}_{2M \times M}}} \right]^{\text{T}}} , 设{\lambda _m} 为第m 个非零奇异值,{{\boldsymbol{\varLambda }}_{2M}} = {\text{diag}}\left( {{\lambda _1}, \cdots ,{\lambda _{2M}}} \right) , 且{\lambda _1} \geqslant {\lambda _2} \geqslant \cdots \geqslant {\lambda _{2M}} ;{\boldsymbol{V}} 是{{\boldsymbol{R}}_{uv}} 的右奇异向量, 是2M \times 2M 维酉矩阵,{\boldsymbol{U}} 是{{\boldsymbol{R}}_{uv}} 的左奇异向量, 是3M \times 3M 维酉矩阵, 以{{\boldsymbol{\varLambda }}_{2M}} 对应列的左奇异向量构造3M \times 2M 维矩阵{{\boldsymbol{U}}_u} ,{{\boldsymbol{U}}_u} = {\boldsymbol{U}}{\left[ {{{\boldsymbol{I}}_{2M \times 2M}},{{\boldsymbol{0}}_{2M \times M}}} \right]^{\text{T}}}. (30) 已知
{\boldsymbol{U}} ,{\boldsymbol{V}} 均为酉矩阵, 有{{\boldsymbol{U}}^{\text{H}}}{\boldsymbol{U}} = {{\boldsymbol{I}}_{3M \times 3M}}, {{\boldsymbol{V}}^{\text{H}}}{\boldsymbol{V}}{\text{=}} {{\boldsymbol{I}}_{2M \times 2M}} , 那么根据式(29)可以推得\begin{split}& {{\boldsymbol{R}}_{uv}}{\boldsymbol{R}}_{uv}^{\text{H}} = {\boldsymbol{U}}{{\boldsymbol{\varLambda }}_{uv}}{{\boldsymbol{V}}^{\text{H}}}{\boldsymbol{V\varLambda }}_{uv}^{\text{H}}{{\boldsymbol{U}}^{\text{H}}} = {{\boldsymbol{U}}_u}{\boldsymbol{\varLambda }}_{2M}^2{\boldsymbol{U}}_u^{\text{H}}, \\& {\boldsymbol{R}}_{uv}^{\text{H}}{{\boldsymbol{R}}_{uv}} = {\boldsymbol{V\varLambda }}_{uv}^{\text{H}}{{\boldsymbol{U}}^{\text{H}}}{\boldsymbol{U}}{{\boldsymbol{\varLambda }}_{uv}}{{\boldsymbol{V}}^{\text{H}}} = {\boldsymbol{V\varLambda }}_{2M}^2{{\boldsymbol{V}}^{\text{H}}}. \end{split} (31) 式(31)表明,
{{\boldsymbol{R}}_{uv}} 的左奇异向量{\boldsymbol{U}} 等效为{{\boldsymbol{R}}_{uv}}{\boldsymbol{R}}_{uv}^{\text{H}} 的特征向量, 右奇异向量{\boldsymbol{V}} 等效为{\boldsymbol{R}}_{uv}^{\text{H}}{{\boldsymbol{R}}_{uv}} 的特征向量, 非零奇异值{{\boldsymbol{\varLambda }}_{2M}} 的平方对应{{\boldsymbol{R}}_{uv}}{\boldsymbol{R}}_{uv}^{\text{H}} 与{\boldsymbol{R}}_{uv}^{\text{H}}{{\boldsymbol{R}}_{uv}} 的特征值。借鉴特征子空间的分析方法, 建立奇异向量{\boldsymbol{U}},{\boldsymbol{V}} 与阵列流形{{\boldsymbol{A}}_u}\left( \theta \right),\, {{\boldsymbol{A}}_v}\left( \theta \right) 的联系。定义
{{\boldsymbol{\varLambda }}_S} 为{{\boldsymbol{R}}_{uv}} 较大的K 个奇异值组成的对角阵{{\boldsymbol{\varLambda }}_S} = {\text{diag}}\left( {{\lambda _1}, \cdots ,{\lambda _K}} \right) ,{{\boldsymbol{\varLambda }}_N} 为其他非零奇异值组成的对角阵,{{\boldsymbol{\varLambda }}_N} = {\text{diag}}\left( {{\lambda _{K + 1}}, \cdots ,{\lambda _{2M}}} \right) , 将{{\boldsymbol{\varLambda }}_S},\,{{\boldsymbol{\varLambda }}_N} 对应的奇异向量划分为信号子空间{{\boldsymbol{U}}_S},\,{{\boldsymbol{V}}_S} 与噪声子空间{{\boldsymbol{U}}_N},{{\boldsymbol{V}}_N} , 这样, 式(29)可以写成\begin{split} {{\boldsymbol{R}}_{uv}} =& \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{U}}_S}}~~{{{\boldsymbol{U}}_N}} \end{array}} \right]{{\boldsymbol{\varLambda }}_{2M}}{\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{V}}_S}}~~{{{\boldsymbol{V}}_N}} \end{array}} \right]^{\text{H}}} = \\& {{\boldsymbol{U}}_S}{{\boldsymbol{\varLambda }}_S}{\boldsymbol{V}}_S^{\text{H}} + {{\boldsymbol{U}}_N}{{\boldsymbol{\varLambda }}_N}{\boldsymbol{V}}_N^{\text{H}}. \end{split} (32) 分别利用式(26)和式(32), 则
{\boldsymbol{R}}_{uv}^H{{\boldsymbol{R}}_{uv}} 可表示为{\boldsymbol{R}}_{uv}^{\text{H}}{{\boldsymbol{R}}_{uv}} = {{\boldsymbol{A}}_v}\left( \theta \right){{\boldsymbol{R}}_S}{\boldsymbol{A}}_u^{\text{H}}\left( \theta \right){{\boldsymbol{A}}_u}\left( \theta \right){{\boldsymbol{R}}_S}{\boldsymbol{A}}_v^{\text{H}}\left( \theta \right) + {\left( {\frac{{\sigma _n^2}}{2}} \right)^2}{{\boldsymbol{I}}_{2M \times 2M}}, (33) {\boldsymbol{R}}_{uv}^{\text{H}}{{\boldsymbol{R}}_{uv}}{\text{ = }}{{\boldsymbol{V}}_S}{\boldsymbol{\varLambda }}_S^2{\boldsymbol{V}}_S^{\text{H}}{\text{ + }}{{\boldsymbol{V}}_N}{\boldsymbol{\varLambda }}_N^2{\boldsymbol{V}}_N^{\text{H}}. (34) 式(33)中
{\boldsymbol{A}}_u^{\text{H}}\left( \theta \right){{\boldsymbol{A}}_u}\left( \theta \right) 可视作对{{\boldsymbol{R}}_S} 的加权, 令{\boldsymbol{R}}_S^{'2} = {{\boldsymbol{R}}_S}{\boldsymbol{A}}_u^{\text{H}}\left( \theta \right){{\boldsymbol{A}}_u}\left( \theta \right){{\boldsymbol{R}}_S} , 可得\begin{split} {\boldsymbol{R}}_{uv}^{\text{H}}{{\boldsymbol{R}}_{uv}}{\text{ = }}&{{\boldsymbol{A}}_v}\left( \theta \right){\boldsymbol{R}}_S^{'2}{\boldsymbol{A}}_v^{\text{H}}\left( \theta \right) + {\left( {\frac{{\sigma _n^2}}{2}} \right)^2}{{\boldsymbol{I}}_{2M \times 2M}}{\text{ = }}\\&{{\boldsymbol{V}}_S}{\boldsymbol{\varLambda }}_S^2{\boldsymbol{V}}_S^{\text{H}}{\text{ + }}{{\boldsymbol{V}}_N}{\boldsymbol{\varLambda }}_N^2{\boldsymbol{V}}_N^{\text{H}}. \end{split} (35) 显然,
{\boldsymbol{R}}_{uv}^{\text{H}}{{\boldsymbol{R}}_{uv}} 为厄米特矩阵, 且其特征向量为{\boldsymbol{V}} 。若将{\boldsymbol{R}}_S^{'2} 视为等效信号协方差矩阵,{\boldsymbol{R}}_S^{'2} 与{\boldsymbol{R}}_S^2 正相关, 则理想条件下{\boldsymbol{R}}_{uv}^{\text{H}}{{\boldsymbol{R}}_{uv}} 的大特征值{\boldsymbol{\varLambda }}_S^2 与信号功率的平方成正相关, 且小特征值{\boldsymbol{\varLambda }}_N^2 满足如下关系:\lambda _{K{\text{ + }}1}^2{\text{ = }} \cdots {\text{ = }}\lambda _{2M}^2{\text{ = }}{\left( {\frac{{\sigma _n^2}}{2}} \right)^2}. (36) 由于奇异值均为实数, 所以, 当空间噪声为白噪声时, 有
{{\boldsymbol{\varLambda }}_N} = \frac{{\sigma _n^2}}{2}{{\boldsymbol{I}}_{(2M{\text{ - }}K) \times (2M{\text{ - }}K)}}. (37) {\boldsymbol{R}}_{uv}^{\text{H}}{{\boldsymbol{R}}_{uv}} 的信号子空间{{\boldsymbol{V}}_S} 与噪声子空间{{\boldsymbol{V}}_N} 正交, 两者包含的特征向量分别为{{\boldsymbol{V}}}_{S}\text=\left[{{\boldsymbol{v}}}_{1},{{\boldsymbol{v}}}_{2},\cdots ,{{\boldsymbol{v}}}_{K}\right]\text{, }~{{\boldsymbol{V}}}_{N}\text=\left[{{\boldsymbol{v}}}_{K + 1},{{\boldsymbol{v}}}_{K + 2},\cdots ,{{\boldsymbol{v}}}_{2M}\right]. (38) 因为通常
M \gt K , 而{{\boldsymbol{A}}_v},\,{{\boldsymbol{A}}_u} 为范德蒙矩阵,{\text{rank}}\left( {{{\boldsymbol{A}}_v}} \right) = {\text{rank}}\left( {{{\boldsymbol{A}}_u}} \right) = K , 则{\text{rank}}\left( {{\boldsymbol{R}}_S^{'2}} \right) = K , 噪声子空间{{\boldsymbol{V}}_N} 与{{\boldsymbol{A}}_v} 正交, 有{\boldsymbol A}_{v}^{\text{H}}{\boldsymbol v}_{j}=0,\, j=K + 1,\cdots ,2M , 即{\text{span}}\left\{ {{{\boldsymbol{v}}_{K + 1}},{{\boldsymbol{v}}_{K + 2}}, \cdots ,{{\boldsymbol{v}}_{2M}}} \right\} \bot {\text{span}}\left\{ {{\boldsymbol{a}}_{v1}^{\text{H}},{\boldsymbol{a}}_{v2}^{\text{H}}, \cdots ,{\boldsymbol{a}}_{vK}^{\text{H}}} \right\}. (39) 因此,
\left\{ {{\boldsymbol{a}}_{v1}^{\text{H}},{\boldsymbol{a}}_{v2}^{\text{H}}, \cdots ,{\boldsymbol{a}}_{vK}^{\text{H}},{{\boldsymbol{v}}_{K + 1}},{{\boldsymbol{v}}_{K + 2}}, \cdots ,{{\boldsymbol{v}}_{2M}}} \right\} 构成2M 维空间一组基底, 而\left\{ {{{\boldsymbol{v}}_1},{{\boldsymbol{v}}_2}, \cdots ,{{\boldsymbol{v}}_K},{{\boldsymbol{v}}_{K + 1}},{{\boldsymbol{v}}_{K + 2}}, \cdots ,{{\boldsymbol{v}}_{2M}}} \right\} 为2M 维空间一组正交基底[21], 所以{\text{span}}\left\{ {{{\boldsymbol{v}}_1},{{\boldsymbol{v}}_2}, \cdots ,{{\boldsymbol{v}}_K}} \right\} = {\text{span}}\left\{ {{\boldsymbol{a}}_{v1}^{\text{H}},{\boldsymbol{a}}_{v2}^{\text{H}}, \cdots ,{\boldsymbol{a}}_{vK}^{\text{H}}} \right\}. (40) 也就是说, 较大奇异值
{{\boldsymbol{\varLambda }}_S} 对应的右奇异向量{{\boldsymbol{V}}_S} 张成的空间, 与{{\boldsymbol{A}}_v} 导向矢量张成的空间为同一个空间。同理可证,{{\boldsymbol{R}}_{uv}}{\boldsymbol{R}}_{uv}^{\text{H}} 的信号子空间{{\boldsymbol{U}}_S} 与噪声子空间{{\boldsymbol{U}}_N} 正交, 它们包含的特征向量分别为{{\boldsymbol{U}}}_{S}\text=\left[{{\boldsymbol{u}}}_{1},{{\boldsymbol{u}}}_{2},\cdots ,{{\boldsymbol{u}}}_{K}\right]\text{, }~{{\boldsymbol{U}}}_{N}\text=\left[{{\boldsymbol{u}}}_{K + 1},{{\boldsymbol{u}}}_{K + 2},\cdots ,{{\boldsymbol{u}}}_{2M}\right]. (41) 有
{{\boldsymbol{A}}}_{u}^{\text{H}}{{\boldsymbol{u}}}_{j}=0, \; j=K + 1,\cdots ,2M , 即{\text{span}}\left\{ {{{\boldsymbol{u}}_{K + 1}},{{\boldsymbol{u}}_{K + 2}}, \cdots ,{{\boldsymbol{u}}_{2M}}} \right\} \bot {\text{span}}\left\{ {{\boldsymbol{a}}_{u1}^{\text{H}},{\boldsymbol{a}}_{u2}^{\text{H}}, \cdots ,{\boldsymbol{a}}_{uK}^{\text{H}}} \right\}. (42) 较大奇异值
{{\boldsymbol{\varLambda }}_S} 对应的左奇异向量{{\boldsymbol{U}}_S} 张成的空间, 与{{\boldsymbol{A}}_u} 的导向矢量张成的空间为同一个空间, 即{\text{span}}\left\{ {{{\boldsymbol{u}}_1},{{\boldsymbol{u}}_2}, \cdots ,{{\boldsymbol{u}}_K}} \right\} = {\text{span}}\left\{ {{\boldsymbol{a}}_{u1}^{\text{H}},{\boldsymbol{a}}_{u2}^{\text{H}}, \cdots ,{\boldsymbol{a}}_{uK}^{\text{H}}} \right\}. (43) 由于声矢量传感器的阵列流形
{{\boldsymbol{A}}_u} 中, 除了振速传感器阵列流形{{\boldsymbol{A}}_v} 外, 还包含声压传感器阵列流形{\boldsymbol{A}} , 相应地, 左奇异向量{\boldsymbol{U}} 较右奇异向量{\boldsymbol{V}} 张成的空间矩阵维数更高、信息量更为丰富, 所以本文选用左奇异向量{\boldsymbol{U}} 和奇异值重构协方差矩阵{{\boldsymbol{R}}_{\rm cmd}} :{{\boldsymbol{R}}_{\rm cmd}} = {\boldsymbol{U}}{\left( {{{\boldsymbol{\varLambda }}_{uv}}{\boldsymbol{\varLambda }}_{uv}^{\text{H}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}{{\boldsymbol{U}}^{\text{H}}} = {{\boldsymbol{U}}_u}{{\boldsymbol{\varLambda }}_{2M}}{\boldsymbol{U}}_u^{\text{H}}. (44) 将
{{\boldsymbol{R}}_{uv}} 和{{\boldsymbol{R}}_{\rm cmd}} 同样写成子空间的表示形式:\begin{split}& {{\boldsymbol{R}}_{\rm cmd}} = {{\boldsymbol{U}}_S}{{\boldsymbol{\varLambda }}_S}{\boldsymbol{U}}_S^{\text{H}}{\text{ + }}{{\boldsymbol{U}}_N}{{\boldsymbol{\varLambda }}_N}{\boldsymbol{U}}_N^{\text{H}}, \\[1.5mm]& {{\boldsymbol{R}}_{uv}} = {{\boldsymbol{U}}_S}{{\boldsymbol{\varLambda }}_S}{\boldsymbol{V}}_S^{\text{H}}{\text{ + }}{{\boldsymbol{U}}_N}{{\boldsymbol{\varLambda }}_N}{\boldsymbol{V}}_N^{\text{H}}. \end{split} (45) 可以发现,
{{\boldsymbol{R}}_{\rm cmd}}{\boldsymbol{R}}_{\rm cmd}^{\text{H}}{\text{ = }}{{\boldsymbol{R}}_{uv}}{\boldsymbol{R}}_{uv}^{\text{H}} , 也就是说,{{\boldsymbol{R}}_{uv}} 和{{\boldsymbol{R}}_{\rm cmd}} 均由同一个矩阵分解而来, 有\begin{split}& {{\boldsymbol{R}}_{\rm cmd}}{\boldsymbol{R}}_{\rm cmd}^{\text{H}}{\text{ = }}{{\boldsymbol{U}}_S}{\boldsymbol{\varLambda }}_S^2{\boldsymbol{U}}_S^{\text{H}}{\text{ + }}{{\boldsymbol{U}}_N}{\boldsymbol{\varLambda }}_N^2{\boldsymbol{U}}_N^{\text{H}} {\text{ = }} \\[2mm]&\quad {{\boldsymbol{U}}_S}{{\boldsymbol{\varLambda }}_S}{\boldsymbol{S}}_S^{\text{H}}{{\boldsymbol{S}}_S}{{\boldsymbol{\varLambda }}_S}{\boldsymbol{U}}_S^{\text{H}}{\text{ + }}{{\boldsymbol{U}}_N}{{\boldsymbol{\varLambda }}_N}{\boldsymbol{S}}_N^{\text{H}}{{\boldsymbol{S}}_N}{{\boldsymbol{\varLambda }}_N}{\boldsymbol{U}}_N^{\text{H}}, \end{split} (46) 式中,
{\boldsymbol{S}}_S^{\text{H}}{{\boldsymbol{S}}_S} = {{\boldsymbol{I}}_{K \times K}},~{\boldsymbol{S}}_N^{\text{H}}{{\boldsymbol{S}}_N} = {{\boldsymbol{I}}_{\left( {2M - K} \right) \times \left( {2M - K} \right)}} 。式(46)还可表示为\begin{split}& {{\boldsymbol{R}}_{\rm cmd}}{\boldsymbol{R}}_{\rm cmd}^{\text{H}} = {{\boldsymbol{R}}_{uv}}{\boldsymbol{R}}_{uv}^{\text{H}} = \\&\quad {{\boldsymbol{A}}_u}\left( \theta \right){{\boldsymbol{R}}_S}{\boldsymbol{A}}_v^{\text{H}}\left( \theta \right){{\boldsymbol{A}}_v}\left( \theta \right){{\boldsymbol{R}}_S}{\boldsymbol{A}}_u^{\text{H}}\left( \theta \right) + {\left( {\frac{{\sigma _n^2}}{2}} \right)^2}{{\boldsymbol{I}}_u}, \end{split} (47) 式中,
{{\boldsymbol{I}}_u}{\text{ = diag}}\left( {0,1,1} \right) \otimes {{\boldsymbol{I}}_{M \times M}} 。由于{{\boldsymbol{R}}_{\rm cmd}} 为厄米特矩阵, 其噪声分量{{\boldsymbol{R}}_{N{\rm cmd}}} = {{\sigma _n^2{{\boldsymbol{I}}_u}} \mathord{\left/ {\vphantom {{\sigma _n^2{{\boldsymbol{I}}_u}} 2}} \right. } 2} , 即{{\boldsymbol{R}}_{\rm cmd}} 的前M行噪声功率被完全消除,{{\boldsymbol{R}}_{N{\rm cmd}}} 等价于{{\boldsymbol{R}}_{uv}} 的噪声协方差{{\boldsymbol{R}}_{N{\rm uv}}} 。根据
{{\boldsymbol{U}}_N} 与{{\boldsymbol{U}}_S} 和{{\boldsymbol{A}}_u} 的正交性, 式(46)和式(47)两侧左乘{{\boldsymbol{U}}_N} 并化简可得{{\boldsymbol{U}}_N}{{\boldsymbol{\varLambda }}_N}{\text{ = }}{{\boldsymbol{R}}_{N{\rm cmd}}}{{\boldsymbol{U}}_N} , 同理, 对{{\boldsymbol{R}}_{uv}} 的式(26)和式(32)两侧左乘{{\boldsymbol{V}}_N} 可得{{\boldsymbol{U}}_N}{{\boldsymbol{\varLambda }}_N}{\text{ = }}{{\boldsymbol{R}}_{N{\rm uv}}}{{\boldsymbol{V}}_N} , 而{{\boldsymbol{R}}_{N{\rm cmd}}} 和{{\boldsymbol{R}}_{N{\rm uv}}} 存在等价关系, 可推得噪声子空间{{\boldsymbol{U}}_N},{{\boldsymbol{V}}_N} 等价, 即理论上矩阵重构前后{{\boldsymbol{R}}_{uv}} 和{{\boldsymbol{R}}_{\rm cmd}} 的噪声子空间并未发生改变。而{{\boldsymbol{R}}_{\rm cmd}} 的信号子空间由{{\boldsymbol{U}}_S} 张成, 与{{\boldsymbol{V}}_S} 相比{{\boldsymbol{U}}_S} 所含信息更为完备, 因此, 矩阵重构后{{\boldsymbol{R}}_{\rm cmd}} 的信号部分得到增强, 也就是说, 利用协方差矩阵{{\boldsymbol{R}}_{\rm cmd}} 可以获得较{{\boldsymbol{R}}_{uv}} 更高的阵处理增益, 具有更优的性能。2.3 基于协方差矩阵分解的MVDR方法
若较大奇异值
{{\boldsymbol{\varLambda }}_S} 对应的左奇异向量{{\boldsymbol{U}}_S} 张成的空间等价于{{\boldsymbol{A}}_u} 的导向矢量张成的空间, 则存在一个满秩矩阵{\boldsymbol{C}} 使得{{\boldsymbol{U}}_S}{\text{ = }}{{\boldsymbol{A}}_u}\left( \theta \right){\boldsymbol{C}}. (48) 将式(48)代入式(44)中, 可将协方差矩阵
{{\boldsymbol{R}}_{\rm cmd}} 的表达式展开为{{\boldsymbol{R}}_{\rm cmd}}{\text{ = }}{{\boldsymbol{A}}_u}\left( \theta \right){\boldsymbol{C}}{{\boldsymbol{\varLambda }}_S}{{\boldsymbol{C}}^{\text{H}}}{\boldsymbol{A}}_u^{\text{H}}\left( \theta \right) + \frac{{\sigma _n^2}}{2}{{\boldsymbol{U}}_N}{\boldsymbol{U}}_N^{\text{H}}. (49) 那么, 协方差矩阵
{{\boldsymbol{R}}_{\rm cmd}} 对应的导向矢量{{\boldsymbol{a}}_u}\left( \theta \right) 应当为{{\boldsymbol{A}}_u} 对应的系数矩阵{{\boldsymbol{T}}_u}\left( \theta \right) 与声压振速联合处理的导向矢量{\boldsymbol{a}}\left( \theta \right) 组合而成, 即{{\boldsymbol{a}}_u}\left( \theta \right) = {\boldsymbol{T}}_u^{\text{H}}\left( \theta \right){\boldsymbol{a}}\left( \theta \right) = {\boldsymbol{u}}\left( \theta \right) \otimes {\boldsymbol{a}}\left( \theta \right). (50) 利用导向矢量
{{\boldsymbol{a}}_u}\left( \theta \right) 和协方差矩阵{{\boldsymbol{R}}_{\rm cmd}} 实施MVDR方法, 要求满足\left\{ \begin{gathered} {{\boldsymbol{w}}^{\text{H}}}{{\boldsymbol{a}}_u}\left( \theta \right) = 1, \\ \mathop {\min }\limits_{\boldsymbol{w}} {{\boldsymbol{w}}^{\text{H}}}{{\boldsymbol{R}}_{\rm cmd}}{\boldsymbol{w}}. \\ \end{gathered} \right. (51) 采用拉格朗日常数法求解, 得到最优权矢量为
{\boldsymbol{w}} = \frac{{{\boldsymbol{R}}_{\rm cmd}^{ - 1}{{\boldsymbol{a}}_u}\left( \theta \right)}}{{{\boldsymbol{a}}_u^{\text{H}}\left( \theta \right){\boldsymbol{R}}_{\rm cmd}^{ - 1}{{\boldsymbol{a}}_u}\left( \theta \right)}}, (52) 通过波束扫描得到基于协方差矩阵分解的MVDR空间谱为
{P_{\rm cmd}}\left( \theta \right) = \frac{1}{{{\boldsymbol{a}}_u^{\text{H}}\left( \theta \right){\boldsymbol{R}}_{\rm cmd}^{ - 1}{{\boldsymbol{a}}_u}\left( \theta \right)}}, (53) 式中,
{{\boldsymbol{R}}_{\rm cmd}}{\text{ = }}{{\boldsymbol{U}}_u}{{\boldsymbol{\varLambda }}_{2M}}{\boldsymbol{U}}_u^{\text{H}} , 且有{\boldsymbol{U}}_u^{\text{H}}{{\boldsymbol{U}}_u}{\text{ = }}{{\boldsymbol{I}}_{2M \times 2M}} 。存在关系{\boldsymbol{U}}_u^\dagger {\text{ = }}{\left( {{\boldsymbol{U}}_u^{\text{H}}{{\boldsymbol{U}}_u}} \right)^{ - 1}}{\boldsymbol{U}}_u^{\text{H}} = {\boldsymbol{U}}_u^{\text{H}} , 上标“^\dagger ”表示广义逆。因此,{{\boldsymbol{R}}_{\rm cmd}} 的逆矩阵可表示为{\boldsymbol{R}}_{\rm cmd}^{ - 1}{\text{ = }}{{\boldsymbol{U}}_u}{\boldsymbol{\varLambda }}_{2M}^{ - 1}{\boldsymbol{U}}_u^{\text{H}}. (54) 基于协方差矩阵分解的MVDR空间谱可进一步化简为
{P_{\rm cmd}}\left( \theta \right) = \frac{1}{{{\boldsymbol{a}}_u^{\text{H}}\left( \theta \right){{\boldsymbol{U}}_u}{\boldsymbol{\varLambda }}_{2M}^{ - 1}{\boldsymbol{U}}_u^{\text{H}}{{\boldsymbol{a}}_u}\left( \theta \right)}}. (55) 3. 数值仿真与分析
仿真条件: 8元半波长等间隔声矢量线列阵, 各等功率窄带入射信源互不相关, 信源功率为
\sigma _k^2 , 各阵元接收噪声为相互独立的零均值高斯白噪声, 声压通道噪声功率为\sigma _n^2 , 快拍数为1000。定义信噪比为{\text{SNR = }}10\lg \left( {{{\sigma _k^2} \mathord{\left/ {\vphantom {{\sigma _k^2} {\sigma _n^2}}} \right. } {\sigma _n^2}}} \right). (56) 本节对比分析了基于协方差矩阵分解的MVDR方法(CMD-VMVDR)、基于Nehorai处理框架的MVDR方法(VMVDR)、固定观测方位声压振速联合处理MVDR方法(FCIP-VMVDR)和扫描观测方位的声压振速联合处理MVDR方法(SCIP-VMVDR)的DOA估计性能。以均方根误差(RMSE)衡量方位估计精度, 若待测信源数目为
K , 入射方向真实值为{\theta _k} , 进行N 次蒙特卡罗试验, 第n 次的估计值为{\widehat \theta _{n,k}} , 则有{\text{RMSE}} = \sqrt {\frac{1}{{NK}}\sum\limits_{n = 1}^N {\sum\limits_{k = 1}^K {{{\left( {{{\widehat \theta }_{n,k}} - {\theta _k}} \right)}^2}} } } . (57) 以目标分辨概率衡量目标分辨能力, 若目标波达方向真实值分别为
{\theta _1},\, {\theta _2} , 估计值分别为{\widehat \theta _1},\, {\widehat \theta _2} , 则当满足以下条件时认为两目标可以被分辨,\left| {{{\widehat \theta }_1} - {\theta _1}} \right| + \left| {{{\widehat \theta }_2} - {\theta _2}} \right| < \left| {{\theta _1} - {\theta _2}} \right|. (58) 目标分辨概率为成功分辨双目标的仿真试验次数占总试验次数的百分比。本节给出的RMSE与目标分辨概率均为200次蒙特卡罗试验的统计结果。
(1)观测方位影响
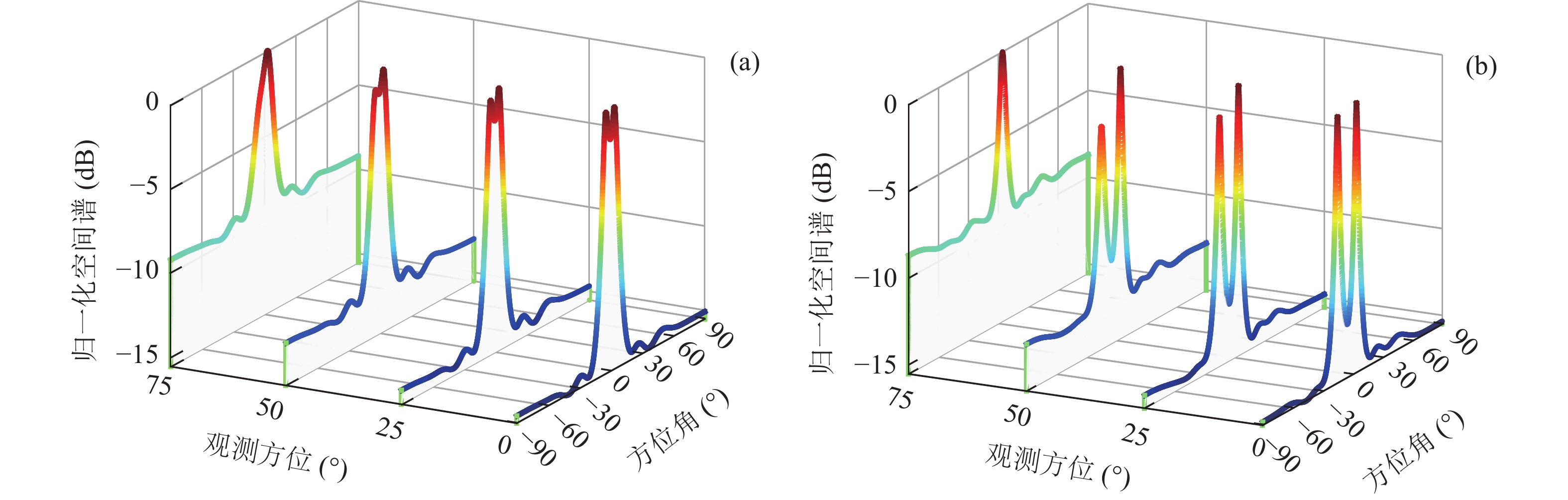
假设信噪比为5 dB, 存在2个信源入射, 图3给出了FCIP-VMVDR在不同观测方位的空间谱, 其中, 图3(a)两目标方位分别为−5°, 4°, 图3(b)两目标方位分别为−15°, 4°。从两图的结果可以看出, 当观测方位处于波达方向附近, 即0°和25°时, FCIP-VMVDR能够分辨方位间隔较小(9°)的两目标, 且具有更低的空间谱背景级; 随着观测方位偏离波达方向, 观测方位为50°时, 距离观测方位较远的信号被明显削弱, 空间谱背景级变高, 两相近目标间的凹槽变浅; 观测方位为75°时, 图3(a)中两目标方位已不能分辨, 图3(b)中波达方向为−15°的目标被完全滤除。这表明FCIP-VMVDR空间谱和目标分辨能力受观测方位影响, 观测方位的偏离可能导致DOA估计性能下降甚至信源漏检。
(2)空间谱比较
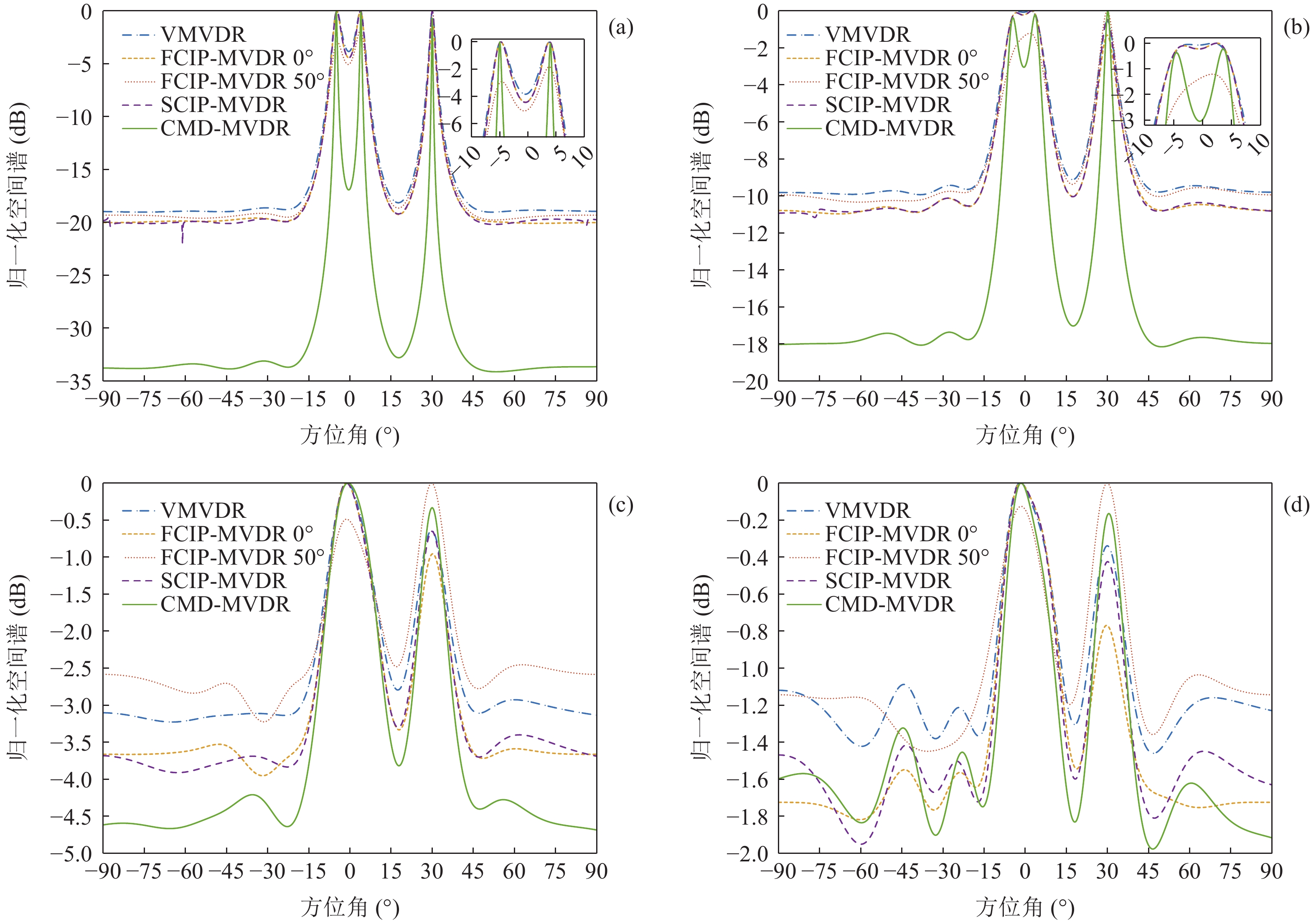
假设存在3个信源分别从−5°, 4°, 30°方向入射, 图4(a)(b)(c)(d)分别给出了信噪比为5 dB, −5 dB, −15 dB, −20 dB时各种方法的空间谱, 其中, FCIP-VMVDR考察了观测方位分别为0°和50°的情况。VMVDR空间谱背景级较高、目标谱峰较钝, 信噪比为−5 dB时就很难分辨出来自−5°和4°的两目标, 如图4(b)所示。SCIP-VMVDR性能较VMVDR有所提升; 而FCIP-VMVDR方法仅在距观测方位较近的目标方位估计中表现出与SCIP-VMVDR相近的性能。观测方位0°的FCIP-VMVDR在信噪比为5 dB, −5 dB时能够分辨−5°, 4°来向的目标, 但削弱了30°来向的目标谱峰, 这种削弱在信噪比为−15 dB和−20 dB时表现得更为明显。而观测方位50°的FCIP-VMVDR能够完成对30°方向入射目标的估计, 但对−5°, 4°来向目标的分辨能力较其他方式更差, 信噪比为5 dB时背景级与SCIP-VMVDR相近, 但−5°, 4°目标谱峰最低、最钝, 信噪比为−5 dB时已完全无法分辨两目标, 信噪比为−15 dB和−20 dB时各种方法均未能成功分辨, 但观测方位50°的FCIP-VMVDR的背景级已高于VMVDR。而CMD-VMVDR方法目标谱峰最为尖锐、对相近目标的分辨性能更优, 在信噪比为5 dB和−5 dB时均能准确估计出−5°, 4°方向目标, 且其空间谱背景级较其他方法更低; 在信噪比为−15 dB时仍较其他方法有着1~2 dB的阵处理增益; 在信噪比为−20 dB时各种方法性能都退化, CMD-VMVDR的空间谱背景级与SCIP-VMVDR相近, 仍优于VMVDR。
(3) DOA估计性能比较
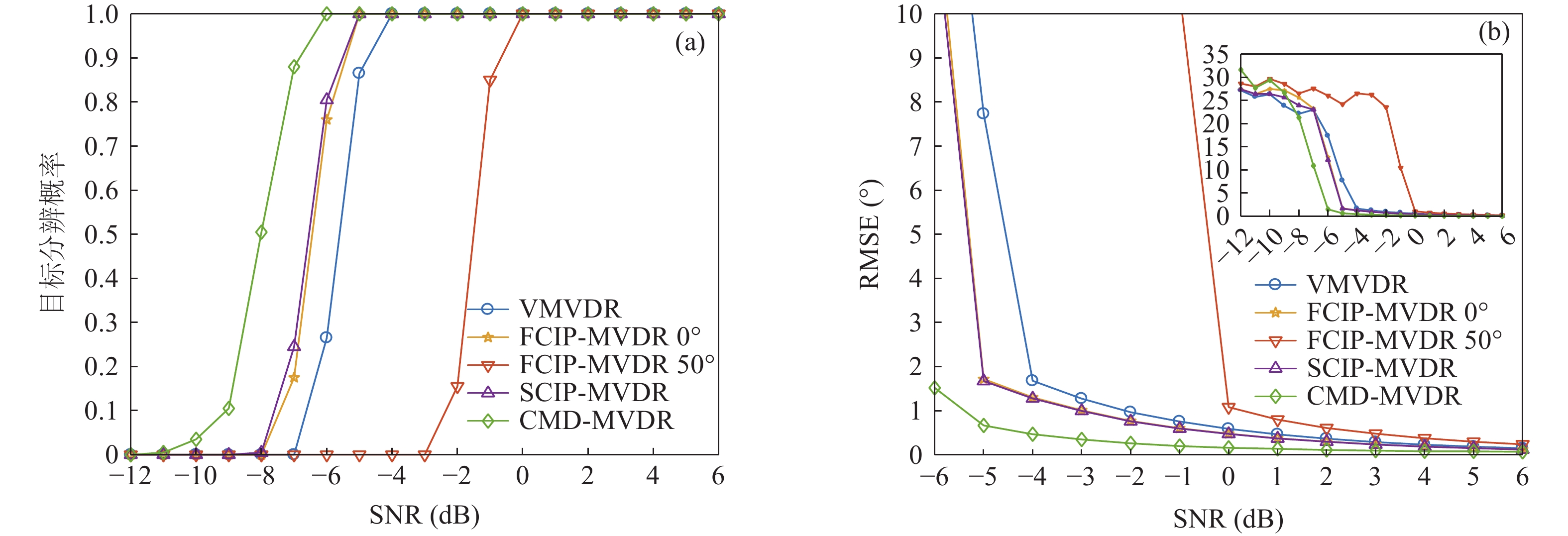
假设存在2个信源分别从−5°和4°方向入射, 图5(a)和图5(b)分别给出了各种方法DOA估计的目标分辨概率和RMSE随信噪比的变化曲线。从图5(a)中可以看出, 随着信噪比的增加, 各种方法的目标分辨概率均有提高。其中, CMD-VMVDR方法在信噪比大于−10 dB时, 已经能够以某种概率分辨两目标; 在信噪比为−7 dB时目标分辨概率接近于0.9, 此时其他方法目标分辨概率均小于0.3; 在信噪比为−6 dB时, CMD-VMVDR最先达到双目标的完全分辨; 当信噪比为−4 dB时, 除观测方位50°的FCIP-VMVDR外, 其他方法目标分辨概率均达到1。图5(b)为对应的均方根误差曲线, 其中插图为均方根误差总体趋势, 可以看出, 随着信噪比增加, 各种方法的RMSE逐渐减小。在信噪比为−6 dB以上时, 随着各种方法目标分辨概率接近1, RMSE的可信度增加, 其中, CMD-VMVDR性能最优; 当信噪比大于−5 dB时, CMD-VMVDR的RMSE低于1°, 观测方位0°的FCIP-VMVDR与SCIP-VMVDR性能接近, 均优于VMVDR, 观测方位50°的FCIP-VMVDR性能最差; 当信噪比为6 dB时, 几种方法的RMSE趋于一致。
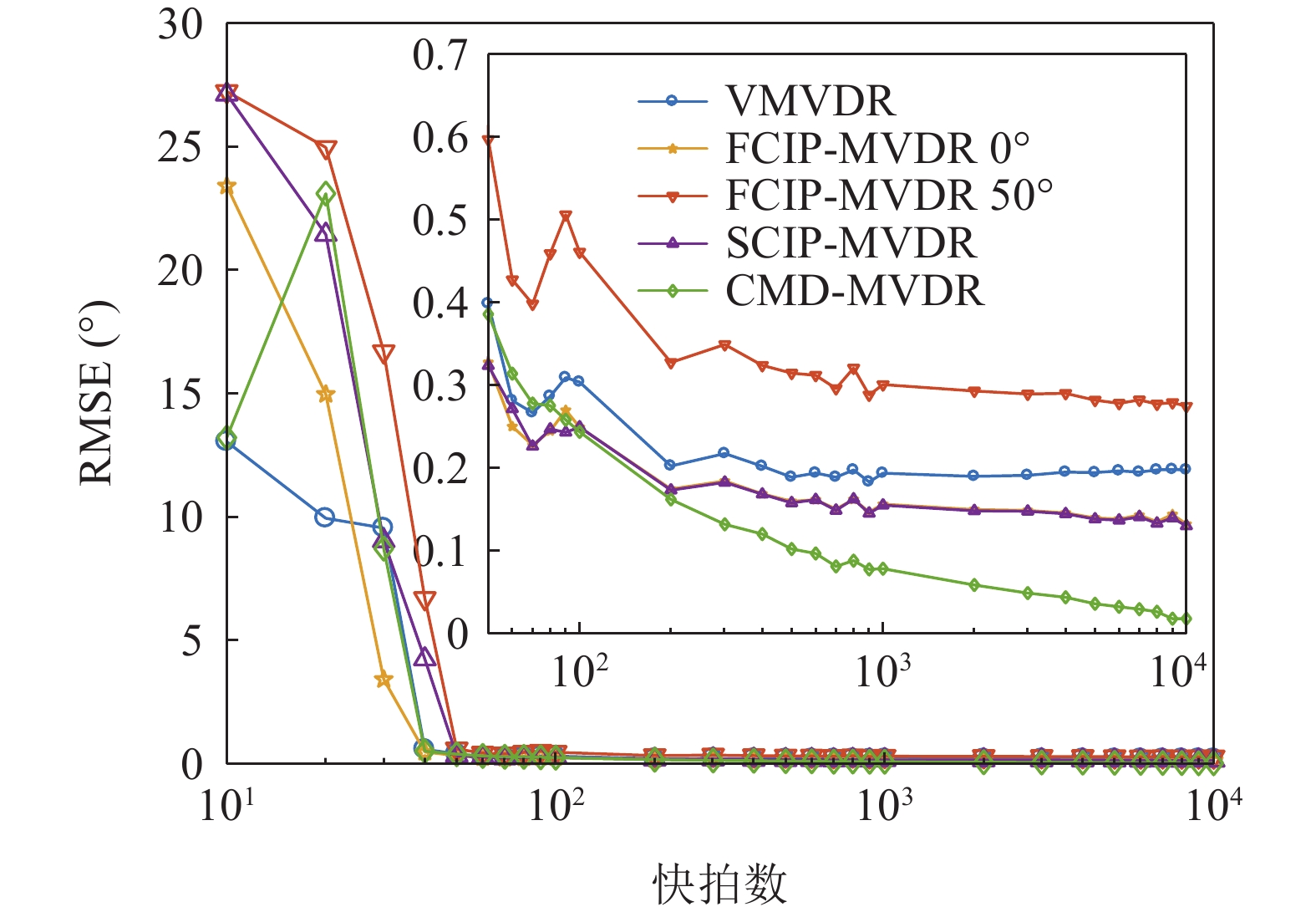
假设信噪比为5 dB, 存在2个信源分别从−5°和4°方向入射, 图6给出了各种方法DOA估计的均方根误差随快拍数的变化曲线, 其中插图为快拍数高于50的RMSE曲线。从图6可以看出, 由于MVDR波束形成器稳健性对快拍数有一定要求, 当快拍数低于50时, 各种方法相继失效, RMSE都较大; 快拍数在50附近时, 除观测方位50°的FCIP-VMVDR外, 其他方法的RMSE相近; 随着快拍数由50增加至200, 各种方法的RMSE呈现抖动下降趋势。本文CMD-VMVDR性能提升最为明显, 在快拍数大于80时RMSE优于VMVDR, 快拍数大于100时RMSE优于SCIP-VMVDR和观测方位为0°的FCIP-VMVDR; 随着快拍数继续增加, VMVDR、FCIP-VMVDR和SCIP-VMVDR的RMSE变化不大, 而CMD-VMVDR的RMSE持续降低, 在快拍数为
{10^4} 时趋向于0。由于受给定信噪比条件下MVDR波束宽度限制, 尽管其他方式能够分辨出两目标, 但因两波束存在重叠, 估计出的双目标间距较实际更小, 即始终存在一定RMSE。而CMD-VMVDR在高快拍条件下协方差矩阵估计更为准确, 阵处理增益更高、波束宽度更窄、目标分辨力更强, 故RMSE可随着两目标方向的准确分辨而逐渐减小。假设信噪比为5 dB, 存在2个信源入射, 两目标方位分别为
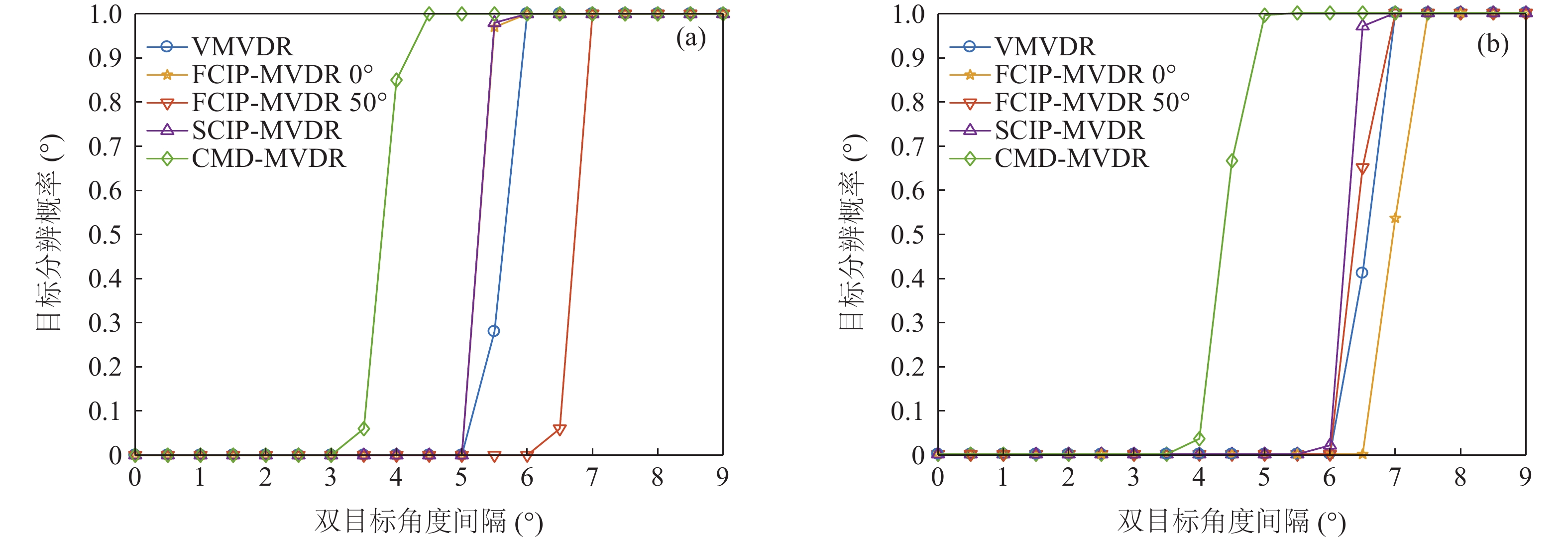
{\theta _S} 和{\theta _S}{\text{ + }}\Delta \theta , 角度间隔\Delta \theta 以0.5°为步长由0°增加到9°, 考虑线列阵对不同方向波束宽度不同, 图7(a)和图7(b)分别给出了起始目标方位{\theta _S} 为−5°和30°条件下, 各种方法的目标分辨概率随两目标角度间隔的变化曲线。整体上各种方法的目标分辨概率在起始目标方位为−5°时较30°更优, 且随着角度间隔的增加, 其目标分辨概率均有提高。其中SCIP-VMVDR相较于VMVDR有近0.5°的双目标分辨优势; 观测方位为0°的FCIP-VMVDR对阵列垂直方向附近入射的两目标估计时, 其目标分辨概率曲线基本与SCIP-VMVDR重合(图7(a)), 对30°附近目标估计时, 其目标分辨概率低于VMVDR (图7(b)); 观测方位为50°的FCIP-VMVDR在距其观测方位较近的目标进行分辨时目标分辨概率高于VMVDR方法(图7(b)), 且双目标角度间隔为6.5°时其目标分辨概率较图7(a)中更优。而CMD-VMVDR具有更强的双目标分辨性能, 在起始目标方位为−5°时较SCIP-VMVDR有1°左右的双目标分辨优势, 且随着目标偏离阵列垂直方向, 波束宽度增加, 双目标分辨优势在起始目标方位为30°时增至1.5°左右。对比图4中各种方法在不同信噪比条件下的空间谱, 可以发现, CMD-MVDR相对其他方法的背景谱抑制能力的优势与信噪比有关, 由于信噪比可以影响噪声子空间对导向矢量的正交性, 高信噪比条件下其性能优势更为显著。由图5可知, 方法的双目标分辨性能也与信噪比有关。下面分析信噪比对CMD-MVDR双目标分辨性能优势的影响, 考虑到图7(a)中SCIP-VMVDR和VMVDR目标分辨概率为1的最小角度间隔均为6°, 但SCIP-VMVDR在角度间隔为5.5°时目标分辨概率明显大于VMVDR的情况, 以目标分辨概率超过0.9为双目标被成功分辨的标准。
假设存在2个信源入射, 两目标方位分别为
{\theta _S} 和{\theta _S}{\text{+}}\Delta \theta , 信源角度间隔\Delta \theta 以0.5°为步长增加, 图8(a)和图8(b)分别给出了起始目标方位{\theta _S} 为−5°和30°条件下, 双目标成功分辨的最小角度间隔随信噪比变化的曲线。整体上各种方法在起始目标方位为−5°时较30°的双目标分辨性能更优, 且随着信噪比增加, 双目标成功分辨的最小角度间隔更小。其中SCIP-VMVDR大体上对VMVDR有0.5°左右的双目标分辨优势; FCIP-VMVDR的双目标分辨性能仍与观测方位和目标波达方向有关, 这与图7的结果一致, 而且低信噪比对观测方位偏离目标方向的FCIP-VMVDR影响更大。随着信噪比由5 dB降至−10 dB, 对0°附近入射的两目标分辨时, 观测方位为50°的FCIP-VMVDR较VMVDR的性能差距由1°增至近2° (图8(a)); 对30°附近入射的两目标分辨时, 观测方位为0°的FCIP-VMVDR较VMVDR的性能差距由0.5°增至1.5° (图8(b))。整体上, CMD-VMVDR的双目标分辨性能在信噪比大于−10 dB时优于VMVDR, 信噪比大于−8 dB时优于SCIP-VMVDR, 且随着信噪比增加, CMD-VMVDR的性能优势更为显著。如图8(a)所示, 信噪比为−5 dB时CMD-VMVDR较VMVDR有1°的双目标分辨优势, 信噪比大于−1 dB时超过1.5°; 随着目标偏离阵列垂直方向, 波束宽度增加, 信噪比为−5 dB时CMD-VMVDR较VMVDR的双目标分辨优势为1.5°左右, 信噪比大于−3 dB时增至2°左右, 如图8(b)所示。(4) 计算量比较
在计算量方面, MVDR方法通过协方差矩阵求逆运算, 以获取该方向上的空间谱值, 设置快拍数为
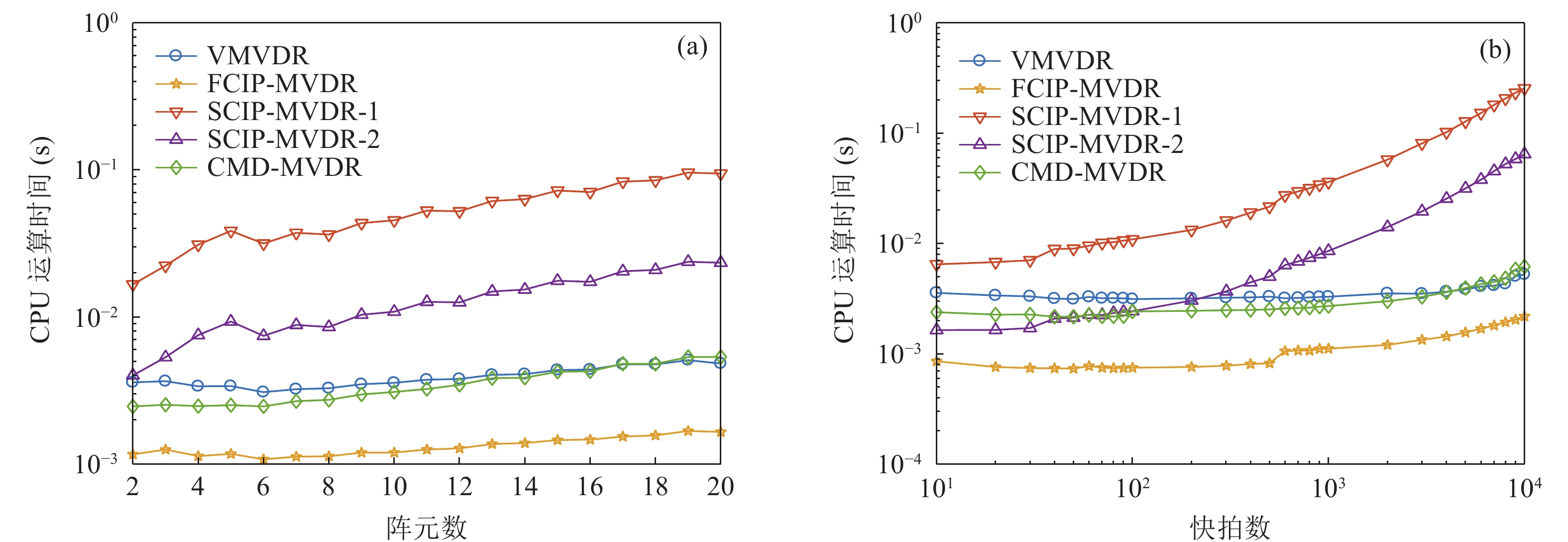
N , VMVDR协方差矩阵维度为3M \times 3M , 算法复杂度为O\left( {9{M^2}N{\text{ + 27}}{M^3}} \right) ; FCIP-VMVDR将振速数据投影到固定观测方位上, 协方差矩阵维度为M \times M , 算法复杂度为O\left( {{M^2}N + {M^3}} \right) ; SCIP-VMVDR需扫描观测方位, 设空间扫描步数为n , 算法复杂度为O\left( {n\left( {{M^2}N + {M^3}} \right)} \right) ; CMD-VMVDR生成3M \times 2M 维协方差矩阵, 尽管需要进行一次奇异值分解运算, 但可以利用其奇异向量和奇异值获得协方差矩阵的逆矩阵, 因此其算法复杂度为O\left( {6{M^2}N{\text{ + 45}}{M^3}} \right) 。各种方法的算法复杂度与快拍数N 和阵元数M 有关, 通常N \gg M > K , K为信源数。SCIP-VMVDR算法复杂度还受空间扫描步数n 影响, 空间扫描步数n 过大, DOA估计精度可以得到保证, 但算法计算量剧增; 空间扫描步数n 过小, 算法计算量下降, 但空间扫描步长增加, 影响DOA估计精度。为定量分析比较各种方法的计算量, 图9(a)和图9(b)分别给出了各种方法DOA估计过程的CPU运算时间随阵元数和快拍数变化的曲线, 其中SCIP-VMVDR考察了空间扫描步数为181和46的情况, 其空间扫描步长分别为1°和4°, 记作SCIP-VMVDR-1和SCIP-VMVDR-2。评估各种方法采用同一运行环境, 电脑配置为Intel(R) Pentium(R) CPU G4560@3.50 GHz, 图中CPU运算时间为200次蒙特卡罗试验的平均结果。
图9(a)中快拍数
N = 1000 , CMD-VMVDR方法的CPU运算时间在2~5 ms之间, 明显低于SCIP-VMVDR, 约为FCIP-VMVDR的3倍, 而略低于VMVDR的CPU运算时间。图9(b)中阵元数M{\text{ = }}8 , CMD-VMVDR的CPU运算时间仍与VMVDR相近, 高于FCIP-VMVDR, 而整体上低于SCIP-VMVDR。但由于空间扫描步数为46的SCIP-VMVDR减少了空间谱值计算次数, 在快拍数小于50的CPU运算时间低于CMD-VMVDR, 此时MVDR波束形成器稳健性较差, 且空间扫描步长为4°, 其DOA估计性能无法保证。(5) 阵列通道幅相误差影响分析
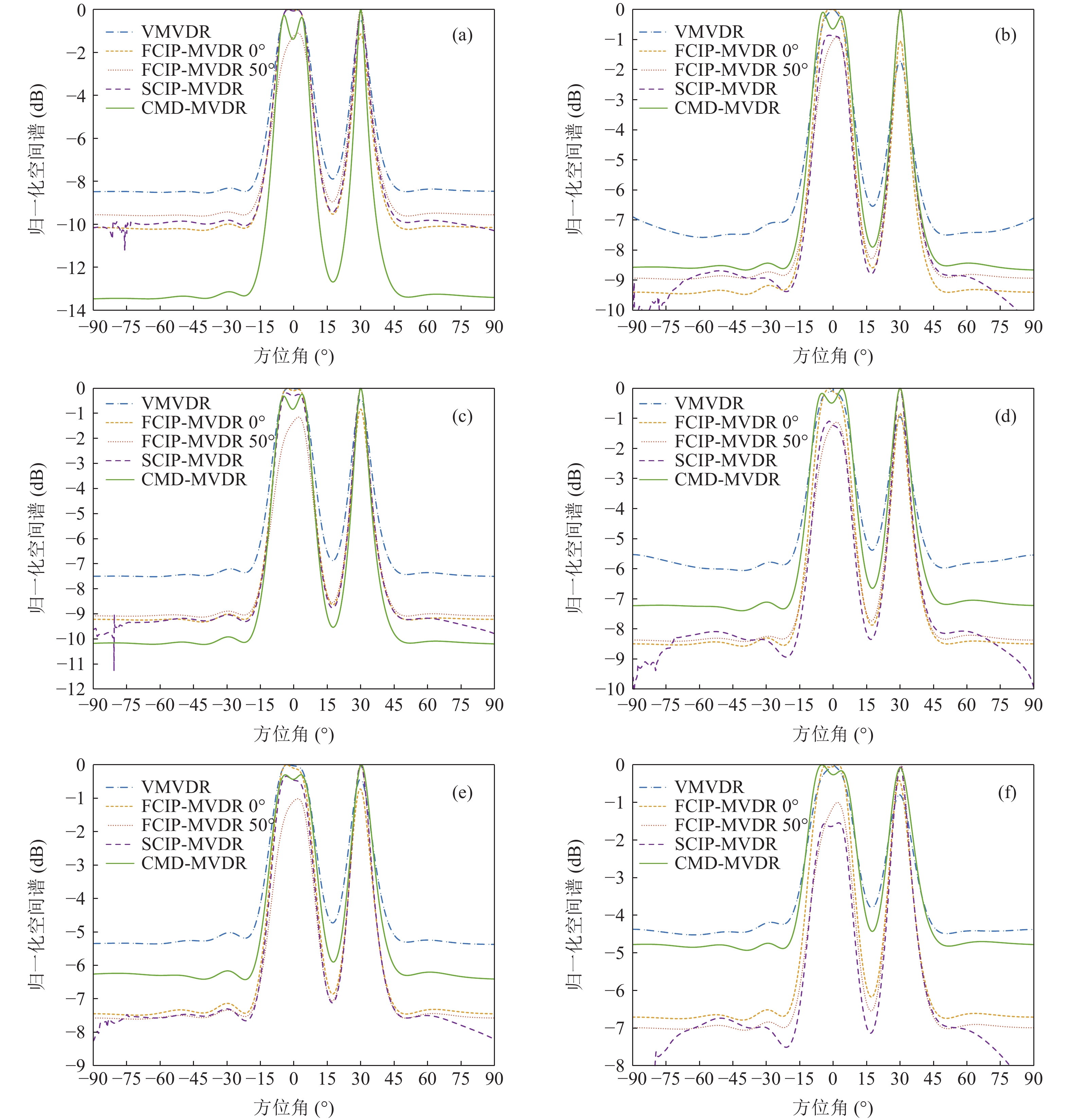
考虑声矢量线列阵各通道幅相误差对DOA估计性能的影响, 假设各通道幅相误差形式为
\left( {1 + {\rho _i}} \right){{\text{e}}^{{\text{j}}{\varphi _i}}} ,{\rho _i} 和{\varphi _i} 分别为第i 个通道的幅度误差和相位误差, 理想条件时{\rho _i} = 0,\, {\varphi _i} = 0 , 存在幅相误差时各通道幅度误差服从均值为0、方差为\sigma _\rho ^2 的高斯分布, 相位误差服从均值为0、方差为\sigma _\varphi ^2 高斯分布。假设信噪比为−5 dB时, 存在3个信源分别从−5°, 4°, 30°方向入射, 图10(a)—图10(f)分别给出了幅度误差方差\sigma _\rho ^2 分别为0.2和0.4, 相位误差方差\sigma _\varphi ^2 分别为5°, 15°, 30°时利用200次蒙特卡罗得到的各方法空间谱。与图4(b)不考虑幅相误差的空间谱相比, 整体上幅相误差的存在使得各方法的DOA均有所下降, 且幅相误差越大, 方法性能下降越严重。相较于VMVDR方法, FCIP-VMVDR方法的阵处理增益对幅相误差表现得更为稳健, 与图4(b)中相比, 其相对VMVDR的背景谱抑制优势有所增加, 但其空域滤波特性仍使远离观测方位的目标强度被削弱。SCIP-VMVDR方法阵处理增益与FCIP-VMVDR相仿, 但背景谱起伏较为剧烈。而本文CMD-VMVDR方法对幅相误差相对较为敏感, 如图10(a)(b)所示, 随着幅度误差方差\sigma _\rho ^2 由0.2增至0.4, 其背景谱抑制优势略逊色于SCIP-VMVDR和FCIP-VMVDR方法。图10中, 随着\sigma _\varphi ^2 由5°增加至30°, CMD-VMVDR方法背景谱随之抬高, 逐渐接近VMVDR方法, 但在\sigma _\rho ^2 = 0.4, \, \sigma _\varphi ^2 = {30\text{°} } 幅相误差较大条件下, CMD-VMVDR方法仍能够完成对−5°和4°方向两相近目标的分辨, 表现出较其他方法更优的目标分辨力, 如图10(f)所示。![]() 图 10 不同幅相误差条件下各方法的空间谱 (a)
图 10 不同幅相误差条件下各方法的空间谱 (a)\sigma _\rho ^2 = 0.2,\; \sigma _\varphi ^2 = {5\text{°}} ; (b)\sigma _\rho ^2 = 0.4,\; \sigma _\varphi ^2 = {5\text{°} } ; (c)\sigma _\rho ^2 = 0.2,\; \sigma _\varphi ^2 = {15\text{°} } ; (d)\sigma _\rho ^2 = 0.4,\; \sigma _\varphi ^2 = {15\text{°} } ; (e)\sigma _\rho ^2 = 0.2,\; \sigma _\varphi ^2 = {30\text{°}} ; (f)\sigma _\rho ^2 = 0.4,\; \sigma _\varphi ^2 = {30\text{°} } 考虑到MVDR波束形成器中, 幅相误差引起的阵处理增益的损失还与信噪比有关[22-23], 假设幅度误差方差
\sigma _\rho ^2 = 0.4 , 相位误差方差\sigma _\varphi ^2 = {15\text{°} } , 图11(a)和图11(b)分别给出了信噪比为5 dB和−15 dB时利用200次蒙特卡罗得到的各方法空间谱。对比图4、图10(c)和图11, 可以发现, 信噪比越低, MVDR阵处理增益对幅相误差越不敏感, 越接近图4中不存在幅相误差的空间谱。本文CMD-VMVDR方法在5 dB的高信噪比时阵增益退化至接近VMVDR, 在较低信噪比−5 dB和−15 dB时的性能优势更为明显。4. 结论
本文针对传统声压振速联合处理中观测方位选择的问题, 提出了一种基于协方差矩阵分解的声压振速联合处理MVDR方法。该方法将声压振速互协方差矩阵分解为观测方位系数矩阵和剩余协方差矩阵, 将系数矩阵与导向矢量结合解决了观测方位选择的难题。为保证协方差矩阵是方阵, 通过对剩余协方差矩阵的奇异值分解完成了厄米特协方差矩阵的重构, 提高了阵处理增益。基于MVDR波束形成器进行了数值仿真, 比较了本文方法与Nehorai处理方法及传统声压振速联合处理中固定观测方位方法、扫描观测方位方法的性能。仿真结果表明, 本文方法具有与Nehorai处理方法相当的计算量, 但通过比较不同信噪比条件下的空间谱, 发现本文方法具有更优的空间谱背景级抑制能力, 并且, 在信噪比、快拍数和双目标角度间隔的维度上本文方法具有更优的双目标分辨能力和分辨概率。此外, 本文方法对阵列通道幅相误差相对敏感, 但其目标分辨能力仍优于其他方法, 且阵处理增益在较低信噪比条件下仍具有一定优势。后续将对算法的稳健性问题及其改进方法进行更深入的理论和实验研究, 以充分验证本文方法的性能。由于本文方法未对阵列流形矩阵进行限制, 可推广应用于声矢量圆阵、面阵等其他阵型的目标方位估计问题。
-
图 10 不同幅相误差条件下各方法的空间谱 (a)
\sigma _\rho ^2 = 0.2,\; \sigma _\varphi ^2 = {5\text{°}} ; (b)\sigma _\rho ^2 = 0.4,\; \sigma _\varphi ^2 = {5\text{°} } ; (c)\sigma _\rho ^2 = 0.2,\; \sigma _\varphi ^2 = {15\text{°} } ; (d)\sigma _\rho ^2 = 0.4,\; \sigma _\varphi ^2 = {15\text{°} } ; (e)\sigma _\rho ^2 = 0.2,\; \sigma _\varphi ^2 = {30\text{°}} ; (f)\sigma _\rho ^2 = 0.4,\; \sigma _\varphi ^2 = {30\text{°} } -
[1] 张君, 陈志菲, 常继红, 等. 声矢量锥形阵的高阶累积量波达方向估计. 声学学报, 2019; 44(6): 970—985 DOI: 10.15949/j.cnki.0371-0025.2019.06.003 [2] 郭俊媛, 杨士莪, 朴胜春, 等. 基于超指向性多极子矢量阵的水下低频声源方位估计方法研究. 物理学报, 2016; 65(13): 187—200 DOI: 10.7498/aps.65.134303 [3] Guo X, Yang S, Miron S. Low-frequency beamforming for a miniaturized aperture three-by-three uniform rectangular array of acoustic vector sensors. J. Acoust. Soc. Am., 2015; 138(6): 3873—3883 DOI: 10.1121/1.4937759
[4] 邱宏安, 郭兵勇, 尚娟, 等. 基于二阶锥的扩展式矢量阵宽带恒定束宽稳健性设计. 西北工业大学学报, 2011; 29(2): 239—244 DOI: 10.3969/j.issn.1000-2758.2011.02.016 [5] 杨德森, 朱中锐, 田迎泽. 矢量声呐技术理论基础及应用发展趋势. 水下无人系统学报, 2018; 26(3): 185—192 DOI: 10.11993/j.issn.2096-3920.2018.03.001 [6] 姚直象, 胡金华, 姜可宇. 矢量阵两类阵处理方法研究. 兵工学报, 2012; 33(9): 1138—1142 [7] Nehorai A, Paldi E. Acoustic vector-sensor array processing. IEEE Trans. Signal Process., 1994; 42(9): 2481—2491 DOI: 10.1109/78.317869
[8] Hawkes M, Nehorai A. Acoustic vector-sensor beamforming and Capon direction estimation. IEEE Trans. Signal Process., 1998; 46(9): 2291—2304 DOI: 10.1109/78.709509
[9] 马伯乐, 朱世强, 孙贵青. 一种声矢量阵最小方差无畸变方位估计算法. 兵工学报, 2019; 40(1): 153—158 DOI: 10.3969/j.issn.1000-1093.2019.01.018 [10] 白兴宇, 姜煜, 赵春晖. 基于声压振速联合处理的声矢量阵信源数检测与方位估计. 声学学报, 2008; 33(1): 56—61 DOI: 10.15949/j.cnki.0371-0025.2008.01.011 [11] Hawkes M, Nehorai A. Acoustic vector-sensor correlations in ambient noise. IEEE J. Oceanic Eng., 2001; 26(3): 337—347 DOI: 10.1109/48.946508
[12] 孙贵青, 杨德森, 时胜国. 基于矢量水听器的声压和质点振速的空间相关系数. 声学学报, 2003; 28(6): 509—513 DOI: 10.3321/j.issn:0371-0025.2003.06.005 [13] 白兴宇, 杨德森, 赵春晖. 基于声压振速联合信息处理的声矢量阵相干信号子空间方法. 声学学报, 2006; 31(5): 410—417 DOI: 10.3321/j.issn:0371-0025.2006.05.004 [14] 姚直象, 胡金华, 姚东明. 基于多重信号分类法的一种声矢量阵方位估计算法. 声学学报, 2008; 33(4): 305—309 DOI: 10.3321/j.issn:0371-0025.2008.04.004 [15] 梁国龙, 马巍, 范展, 等. 矢量声纳高速运动目标稳健高分辨方位估计. 物理学报, 2013; 62(14): 282—290 DOI: 10.7498/aps.62.144302 [16] 姚直象, 姜可宇, 郭瑞, 等. 基于声压振速联合处理的矢量阵旋转不变子空间方位估计方法. 北京理工大学学报, 2012; 32(5): 513—516, 521 DOI: 10.3969/j.issn.1001-0645.2012.05.016 [17] 赵羽. 矢量阵阵处理研究. 博士学位论文, 哈尔滨: 哈尔滨工程大学, 2004: 49—73 [18] 惠俊英, 刘宏, 余华兵, 等. 声压振速联合信息处理及其物理基础初探. 声学学报, 2000; 25(4): 303—307 DOI: 10.3321/j.issn:0371-0025.2000.04.003 [19] 向悠扬, 惠娟, 郭嘉宾, 等. 声矢量阵联合信息处理的信源数估计算法. 哈尔滨工程大学学报, 2022; 43(5): 706—712 DOI: 10.11990/jheu.202009050 [20] Stoica P, Nehorai A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process., 1989; 37(5): 720—741 DOI: 10.1109/29.17564
[21] 高世伟, 保铮. 利用数据矩阵分解实现对空间相关信号源的超分辨处理. 通信学报, 1988(1): 4—13 [22] 曹圣红. 存在阵列误差条件下波达方向估计算法研究. 博士学位论文, 合肥: 中国科学技术大学, 2014: 43—65 [23] 刘凯, 梁国龙, 嵇建飞, 等. 随机阵列误差影响下的声矢量阵噪声特性和阵增益. 哈尔滨工程大学学报, 2011; 32(5): 624—631 DOI: 10.3969/j.issn.1006-7043.2011.05.015 -
期刊类型引用(1)
1. 王立府,王鹏. 基于深度学习的原子范数最小化无网格DOA估计方法. 测试技术学报. 2025(02): 218-229 .  百度学术
百度学术
其他类型引用(1)




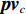
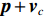
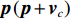
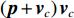
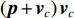
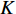
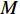
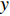
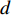
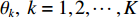
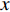
 下载:
下载: