使用协方差矩阵分解的矢量阵声压振速联合处理波达方向估计

张旭; 时胜国; 朱晓春; 徐付佳

doi:10.12395/0371-0025.2022005

使用协方差矩阵分解的矢量阵声压振速联合处理波达方向估计

张旭^{1, 2, 3,},
时胜国^{1, 2, 3, ,},
朱晓春^{1, 2, 3},
徐付佳^{1, 2, 3}

1.
哈尔滨工程大学水声技术全国重点实验室　哈尔滨　150001
2.
工业和信息化部海洋信息获取与安全工信部重点实验室(哈尔滨工程大学)　哈尔滨　150001
3.
哈尔滨工程大学水声工程学院　哈尔滨　150001

详细信息

作者简介:
张旭, zhangxu29@hrbeu.edu.cn

通讯作者:
时胜国, shishengguo@hrbeu.edu.cn

PACS:
计量
- 文章访问数: 283
- HTML全文浏览量: 36
- PDF下载量: 89
出版历程
- 收稿日期: 2022-06-05
- 修回日期: 2022-10-29
- 网络出版日期: 2023-09-11
- 刊出日期: 2023-09-11

Direction of arrival estimation of acoustic vector sensor array based on the combined information processing of pressure and particle velocity using covariance matrix decomposition

ZHANG Xu^{1, 2, 3,},
SHI Shengguo^{1, 2, 3, ,},
ZHU Xiaochun^{1, 2, 3},
XU Fujia^{1, 2, 3}

1.
National Key Laboratory of Underwater Acoustic Technology, Harbin Engineering University　Harbin　150001
2.
Key Laboratory of Marine Information Acquisition and Security (Harbin Engineering University), Ministry of Industry and Information Technology　Harbin　150001
3.
College of Underwater Acoustic Engineering, Harbin Engineering University　Harbin　150001

摘要

摘要:
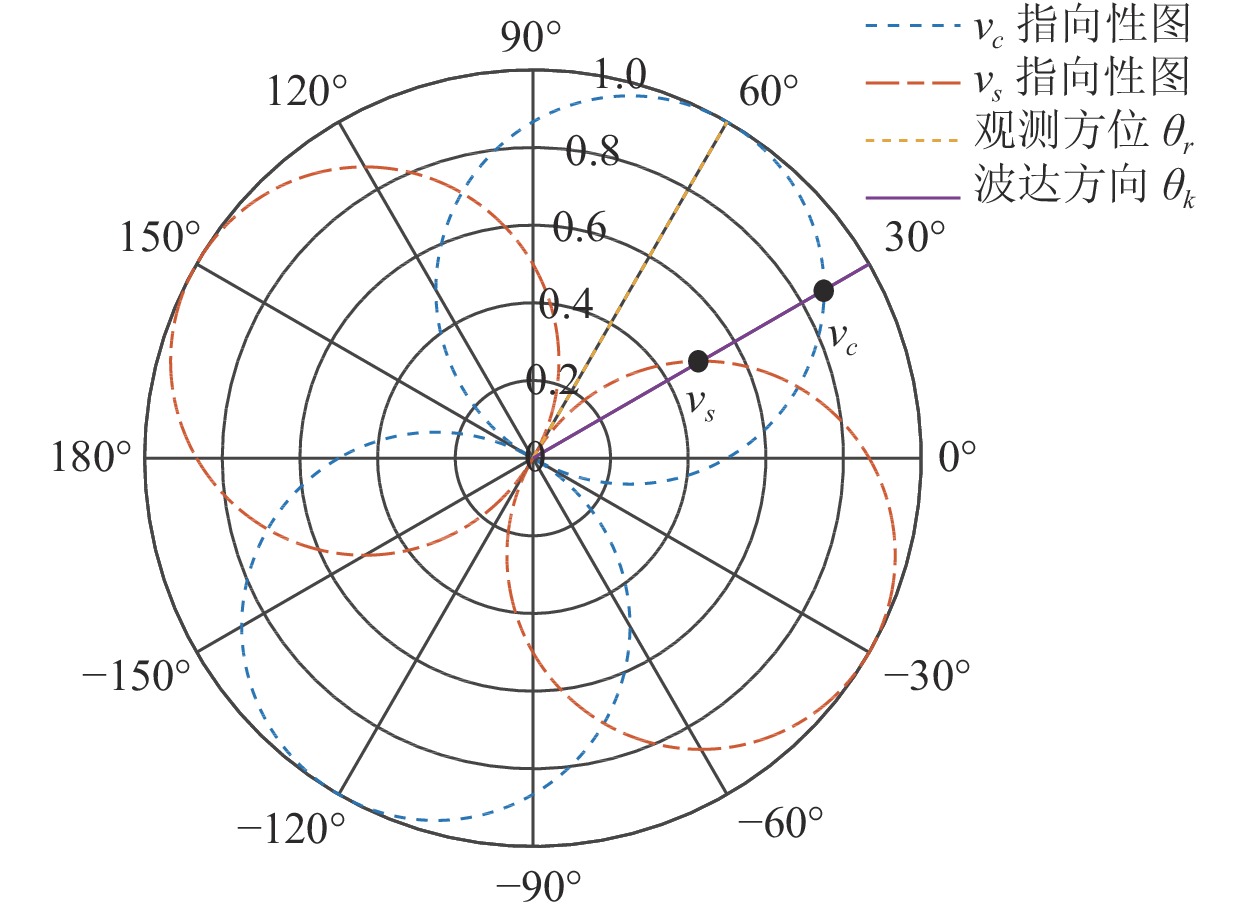
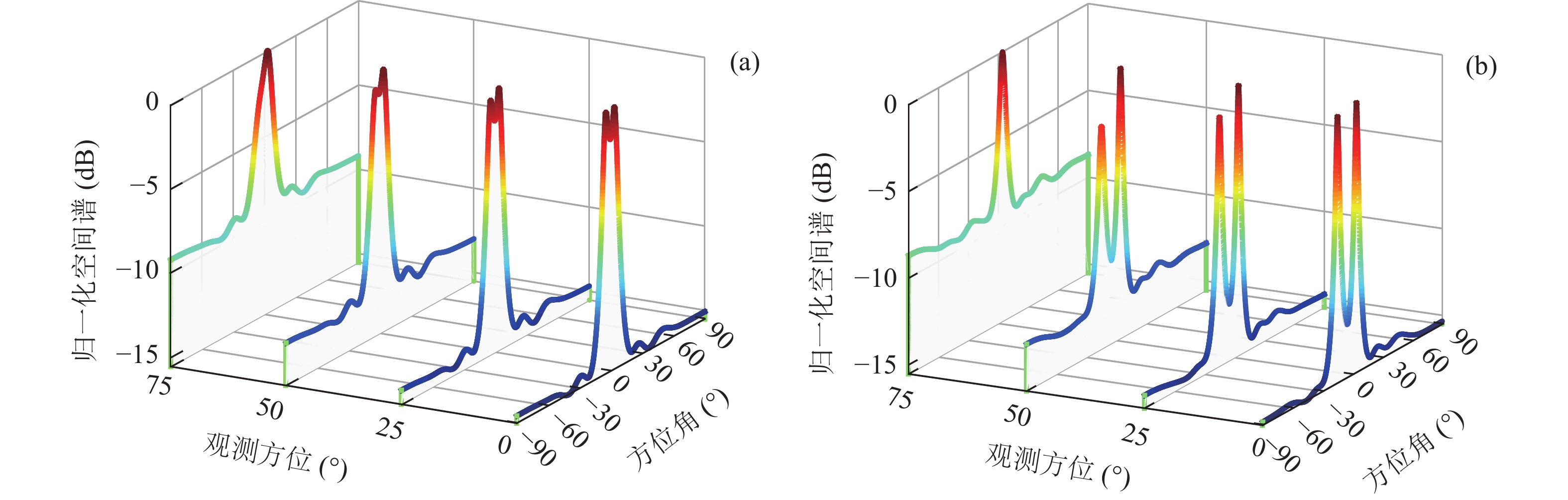
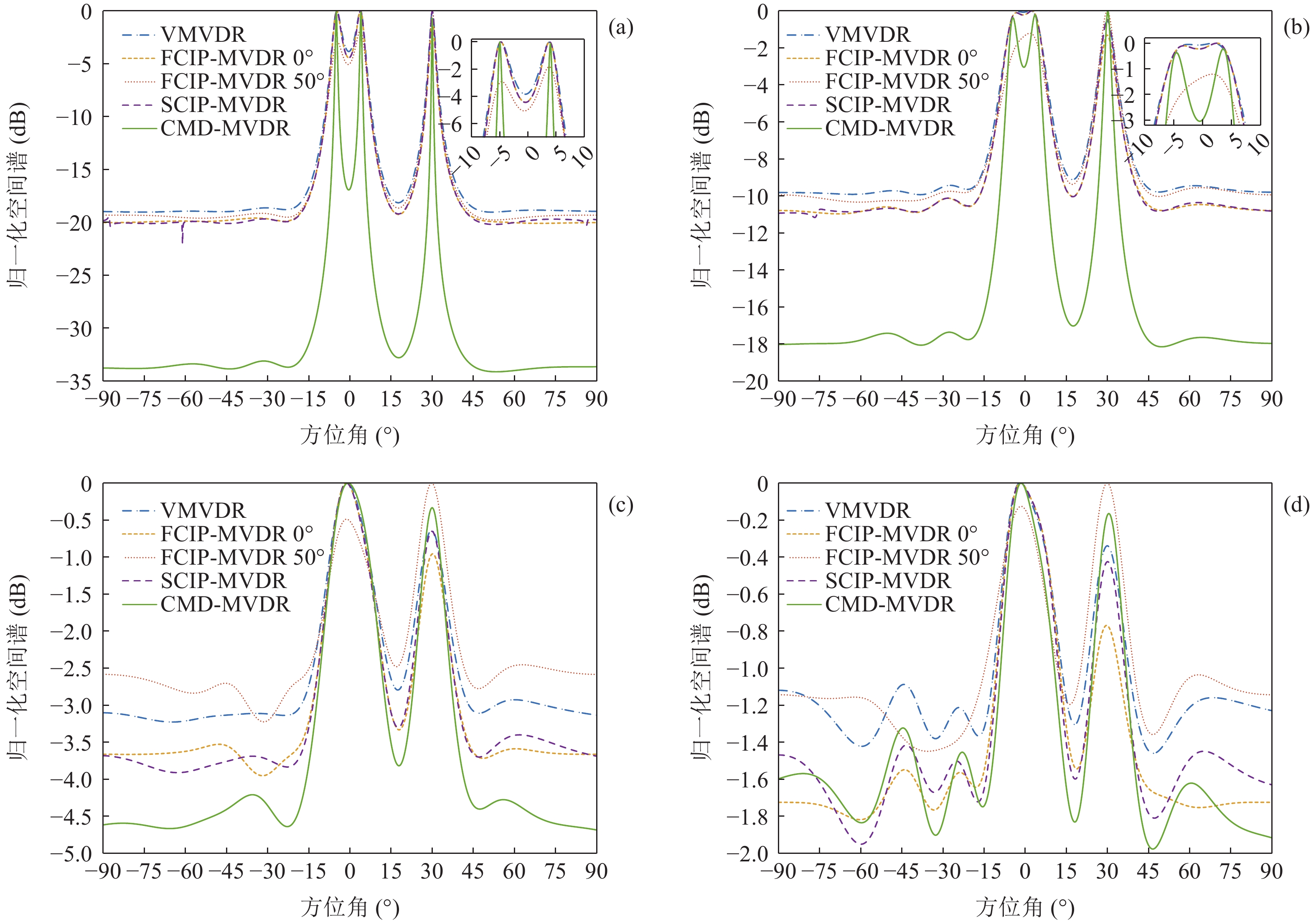
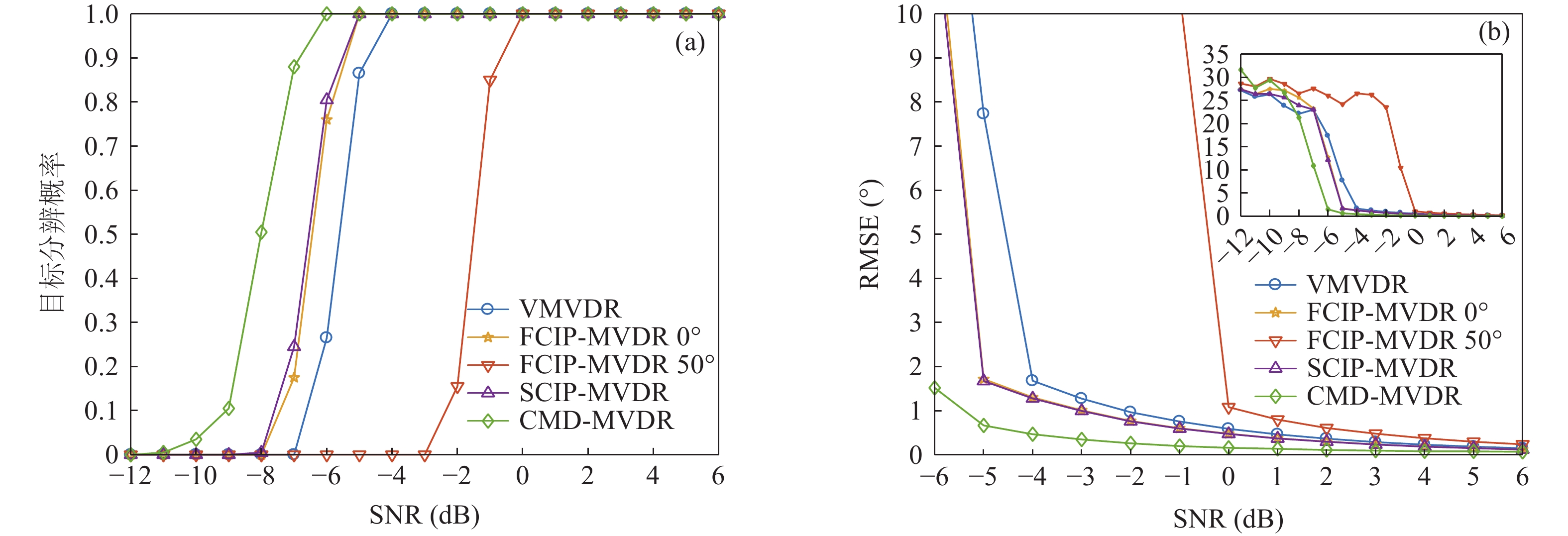
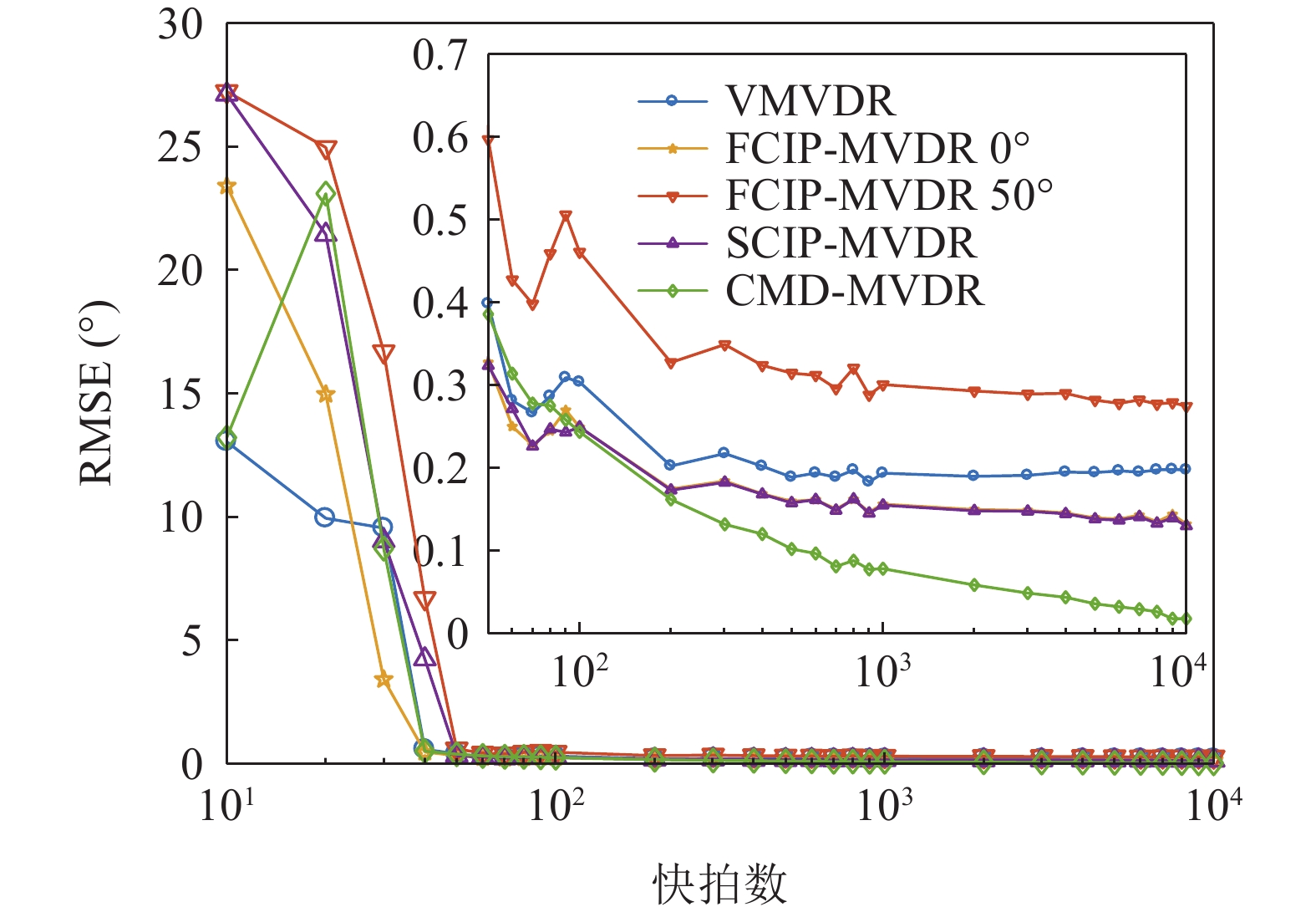
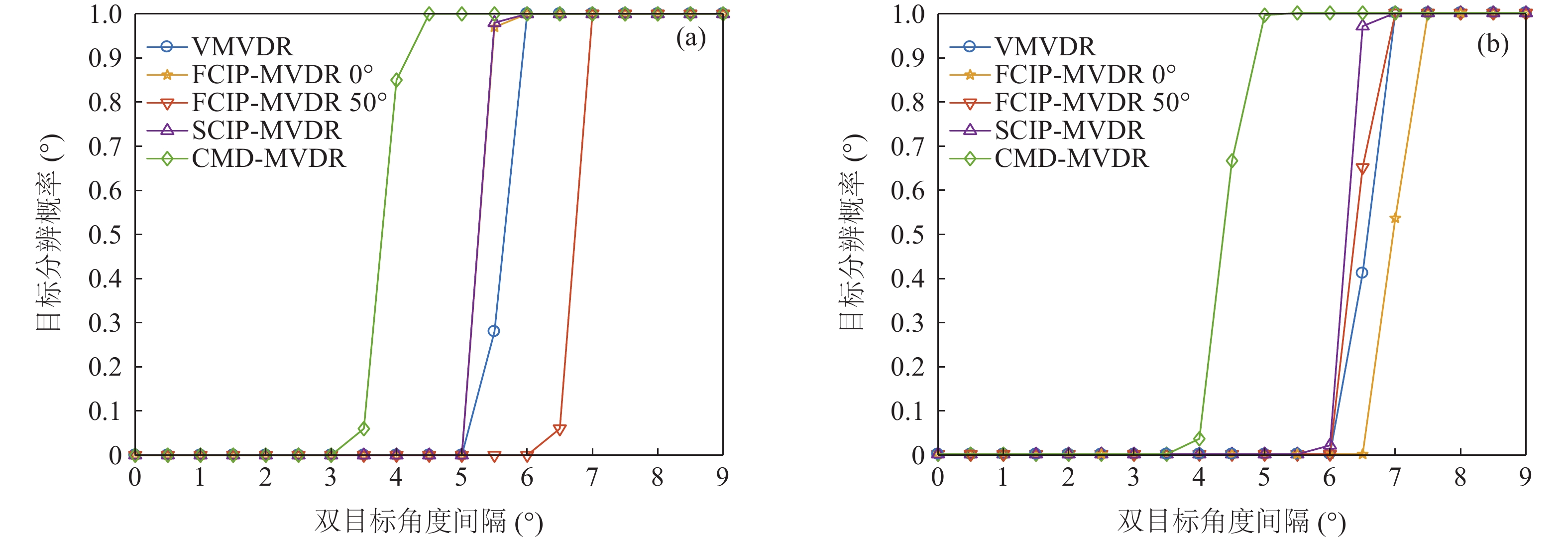
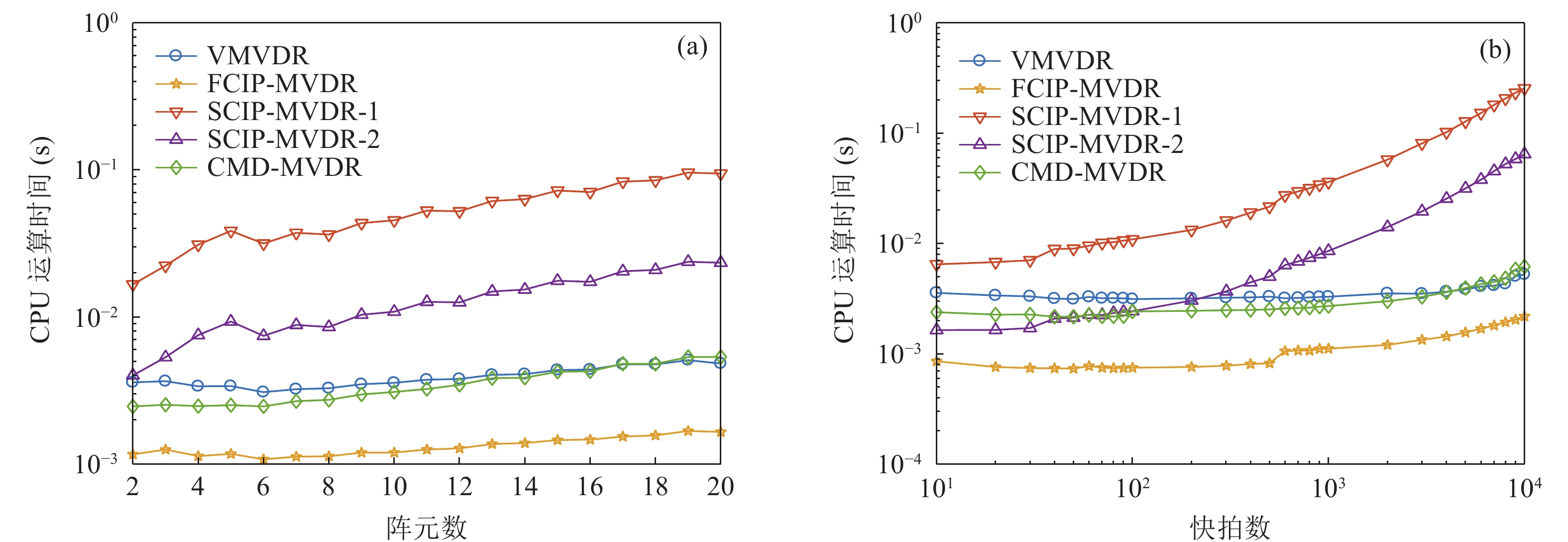
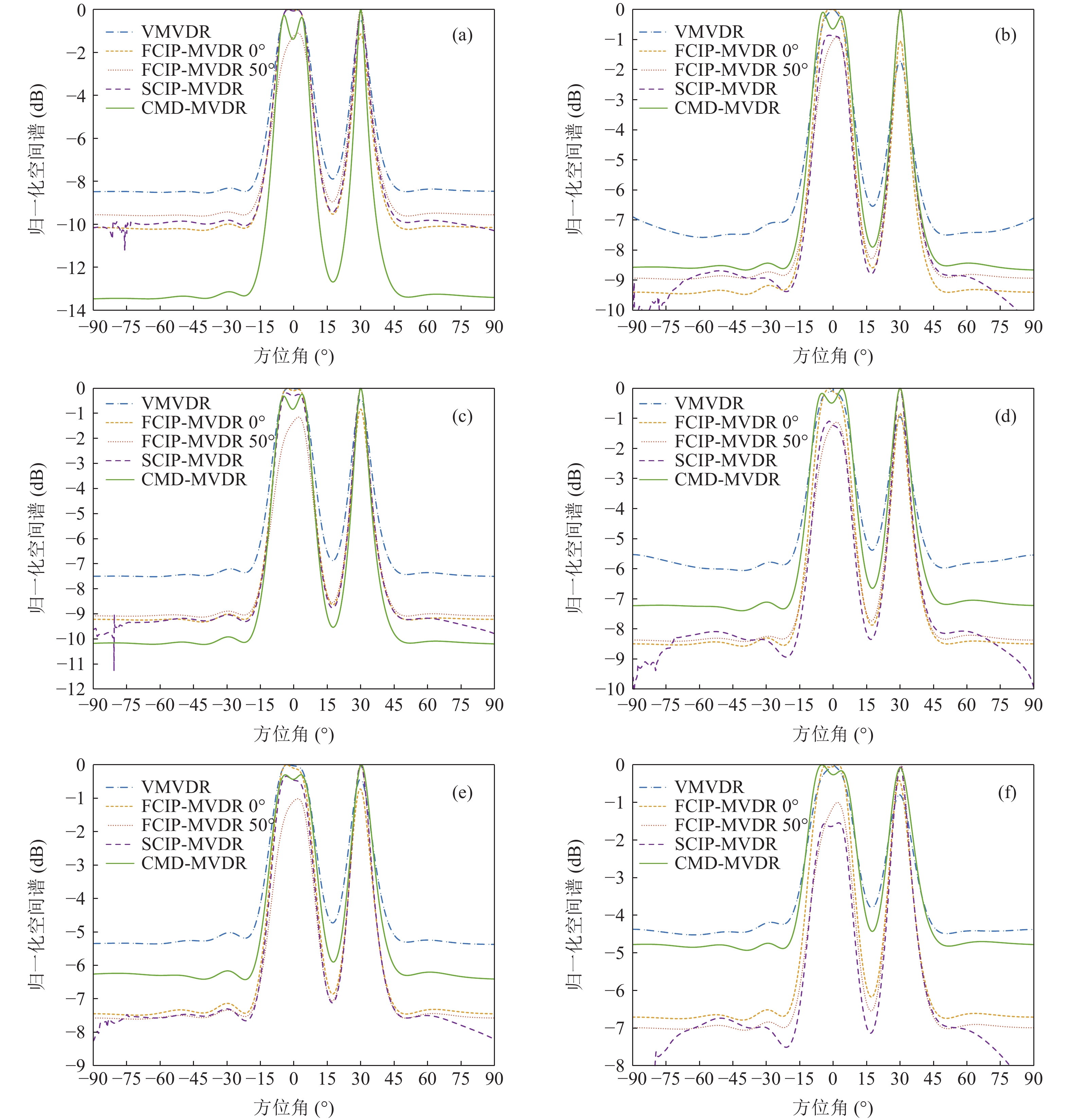
提出一种使用协方差矩阵分解(CMD)的声矢量阵声压振速联合处理方法。该方法将声压振速互协方差矩阵分解为观测方位系数矩阵和剩余协方差矩阵, 将系数矩阵与导向矢量结合避免了观测方位的选择, 对剩余协方差矩阵进行奇异值分解并重构厄米特协方差矩阵, 最后对重构的协方差矩阵实施最小方差无失真响应(MVDR)方法处理。理论分析表明, 使用重构的协方差矩阵能够获得更高的阵处理增益。数值仿真结果验证了本文方法的计算量与Nehorai处理方法相近, 但较传统声压振速联合处理方法具有更高的阵处理增益和目标分辨能力。
- 声矢量阵 /
- 矩阵分解 /
- 奇异值分解 /
- 观测方位 /
- 波达方向估计
Abstract:
A combined processing method of pressure and particle velocity (PV-CPM) for acoustic vector sensor array using covariance matrix decomposition (CMD) is proposed. In this method, the cross-covariance matrix of pressure and particle velocity is decomposed into an observation angle coefficient matrix and a residual covariance matrix. To avoid choosing the observation angle, the coefficient matrix is combined with the guidance vector. By adopting the singular value decomposition, the residual covariance matrix is reconstructed into the new Hermitian covariance matrix, which is ultimately used to implement the MVDR beamforming method. Theoretical analysis shows that the new covariance matrix can achieve higher array processing gain. Furthermore, the numerical simulation proves that the computational complexity of the proposed method is similar to that of the Nehorai’s method, but its array processing gain and multi-target resolution are higher than those of the traditional PV-CPM.
- Acoustic vector sensor array /
- Matrix decomposition /
- Singular value decomposition /
- Observation angle /
- Direction of arrival estimation

HTML全文

图 1 声矢量均匀线阵模型

下载: 全尺寸图片幻灯片

图 2 组合振速指向性与观测方位的关系

下载: 全尺寸图片幻灯片

图 3 不同观测方位条件下FCIP-VMVDR空间谱 (a) 双目标角度间隔9°; (b) 双目标角度间隔19°

下载: 全尺寸图片幻灯片

图 4 不同信噪比条件下各种方法的空间谱 (a) SNR = 5 dB; (b) SNR = −5 dB; (c) SNR = −15 dB; (d) SNR = −20 dB

下载: 全尺寸图片幻灯片

图 5 不同信噪比条件下各种方法的性能分析 (a) 目标分辨概率; (b) 均方根误差

下载: 全尺寸图片幻灯片

图 6 不同快拍数条件下各种方法的均方根误差比较

下载: 全尺寸图片幻灯片

图 7 不同双目标角度间隔条件下目标成功分辨概率 (a) 起始目标方位−5°; (b) 起始目标方位30°

下载: 全尺寸图片幻灯片

图 8 不同信噪比条件下双目标成功分辨的最小角度间隔 (a) 起始目标方位−5º; (b) 起始目标方位30º

下载: 全尺寸图片幻灯片

图 9 各种方法CPU运算时间的对比结果 (a) CPU运算时间随阵元数的变化; (b) CPU运算时间随快拍数的变化

下载: 全尺寸图片幻灯片

图 10 不同幅相误差条件下各方法的空间谱 (a) $\sigma _\rho ^2 = 0.2,\; \sigma _\varphi ^2 = {5\text{°}}$ ; (b) $\sigma _\rho ^2 = 0.4,\; \sigma _\varphi ^2 = {5\text{°} }$ ; (c) $\sigma _\rho ^2 = 0.2,\; \sigma _\varphi ^2 = {15\text{°} }$ ; (d) $\sigma _\rho ^2 = 0.4,\; \sigma _\varphi ^2 = {15\text{°} }$ ; (e) $\sigma _\rho ^2 = 0.2,\; \sigma _\varphi ^2 = {30\text{°}}$ ; (f) $\sigma _\rho ^2 = 0.4,\; \sigma _\varphi ^2 = {30\text{°} }$

下载: 全尺寸图片幻灯片

图 11 存在幅相误差条件下不同信噪比各方法的空间谱 (a) SNR= 5 dB; (b) SNR= −15 dB

下载: 全尺寸图片幻灯片

参考文献(23)

[1]	张君, 陈志菲, 常继红, 等. 声矢量锥形阵的高阶累积量波达方向估计. 声学学报, 2019; 44(6): 970—985 DOI: 10.15949/j.cnki.0371-0025.2019.06.003
[2]	郭俊媛, 杨士莪, 朴胜春, 等. 基于超指向性多极子矢量阵的水下低频声源方位估计方法研究. 物理学报, 2016; 65(13): 187—200 DOI: 10.7498/aps.65.134303
[3]	Guo X, Yang S, Miron S. Low-frequency beamforming for a miniaturized aperture three-by-three uniform rectangular array of acoustic vector sensors. J. Acoust. Soc. Am., 2015; 138(6): 3873—3883 DOI: 10.1121/1.4937759
[4]	邱宏安, 郭兵勇, 尚娟, 等. 基于二阶锥的扩展式矢量阵宽带恒定束宽稳健性设计. 西北工业大学学报, 2011; 29(2): 239—244 DOI: 10.3969/j.issn.1000-2758.2011.02.016
[5]	杨德森, 朱中锐, 田迎泽. 矢量声呐技术理论基础及应用发展趋势. 水下无人系统学报, 2018; 26(3): 185—192 DOI: 10.11993/j.issn.2096-3920.2018.03.001
[6]	姚直象, 胡金华, 姜可宇. 矢量阵两类阵处理方法研究. 兵工学报, 2012; 33(9): 1138—1142
[7]	Nehorai A, Paldi E. Acoustic vector-sensor array processing. IEEE Trans. Signal Process., 1994; 42(9): 2481—2491 DOI: 10.1109/78.317869
[8]	Hawkes M, Nehorai A. Acoustic vector-sensor beamforming and Capon direction estimation. IEEE Trans. Signal Process., 1998; 46(9): 2291—2304 DOI: 10.1109/78.709509
[9]	马伯乐, 朱世强, 孙贵青. 一种声矢量阵最小方差无畸变方位估计算法. 兵工学报, 2019; 40(1): 153—158 DOI: 10.3969/j.issn.1000-1093.2019.01.018
[10]	白兴宇, 姜煜, 赵春晖. 基于声压振速联合处理的声矢量阵信源数检测与方位估计. 声学学报, 2008; 33(1): 56—61 DOI: 10.15949/j.cnki.0371-0025.2008.01.011
[11]	Hawkes M, Nehorai A. Acoustic vector-sensor correlations in ambient noise. IEEE J. Oceanic Eng., 2001; 26(3): 337—347 DOI: 10.1109/48.946508
[12]	孙贵青, 杨德森, 时胜国. 基于矢量水听器的声压和质点振速的空间相关系数. 声学学报, 2003; 28(6): 509—513 DOI: 10.3321/j.issn:0371-0025.2003.06.005
[13]	白兴宇, 杨德森, 赵春晖. 基于声压振速联合信息处理的声矢量阵相干信号子空间方法. 声学学报, 2006; 31(5): 410—417 DOI: 10.3321/j.issn:0371-0025.2006.05.004
[14]	姚直象, 胡金华, 姚东明. 基于多重信号分类法的一种声矢量阵方位估计算法. 声学学报, 2008; 33(4): 305—309 DOI: 10.3321/j.issn:0371-0025.2008.04.004
[15]	梁国龙, 马巍, 范展, 等. 矢量声纳高速运动目标稳健高分辨方位估计. 物理学报, 2013; 62(14): 282—290 DOI: 10.7498/aps.62.144302
[16]	姚直象, 姜可宇, 郭瑞, 等. 基于声压振速联合处理的矢量阵旋转不变子空间方位估计方法. 北京理工大学学报, 2012; 32(5): 513—516, 521 DOI: 10.3969/j.issn.1001-0645.2012.05.016
[17]	赵羽. 矢量阵阵处理研究. 博士学位论文, 哈尔滨: 哈尔滨工程大学, 2004: 49—73
[18]	惠俊英, 刘宏, 余华兵, 等. 声压振速联合信息处理及其物理基础初探. 声学学报, 2000; 25(4): 303—307 DOI: 10.3321/j.issn:0371-0025.2000.04.003
[19]	向悠扬, 惠娟, 郭嘉宾, 等. 声矢量阵联合信息处理的信源数估计算法. 哈尔滨工程大学学报, 2022; 43(5): 706—712 DOI: 10.11990/jheu.202009050
[20]	Stoica P, Nehorai A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process., 1989; 37(5): 720—741 DOI: 10.1109/29.17564
[21]	高世伟, 保铮. 利用数据矩阵分解实现对空间相关信号源的超分辨处理. 通信学报, 1988(1): 4—13
[22]	曹圣红. 存在阵列误差条件下波达方向估计算法研究. 博士学位论文, 合肥: 中国科学技术大学, 2014: 43—65
[23]	刘凯, 梁国龙, 嵇建飞, 等. 随机阵列误差影响下的声矢量阵噪声特性和阵增益. 哈尔滨工程大学学报, 2011; 32(5): 624—631 DOI: 10.3969/j.issn.1006-7043.2011.05.015