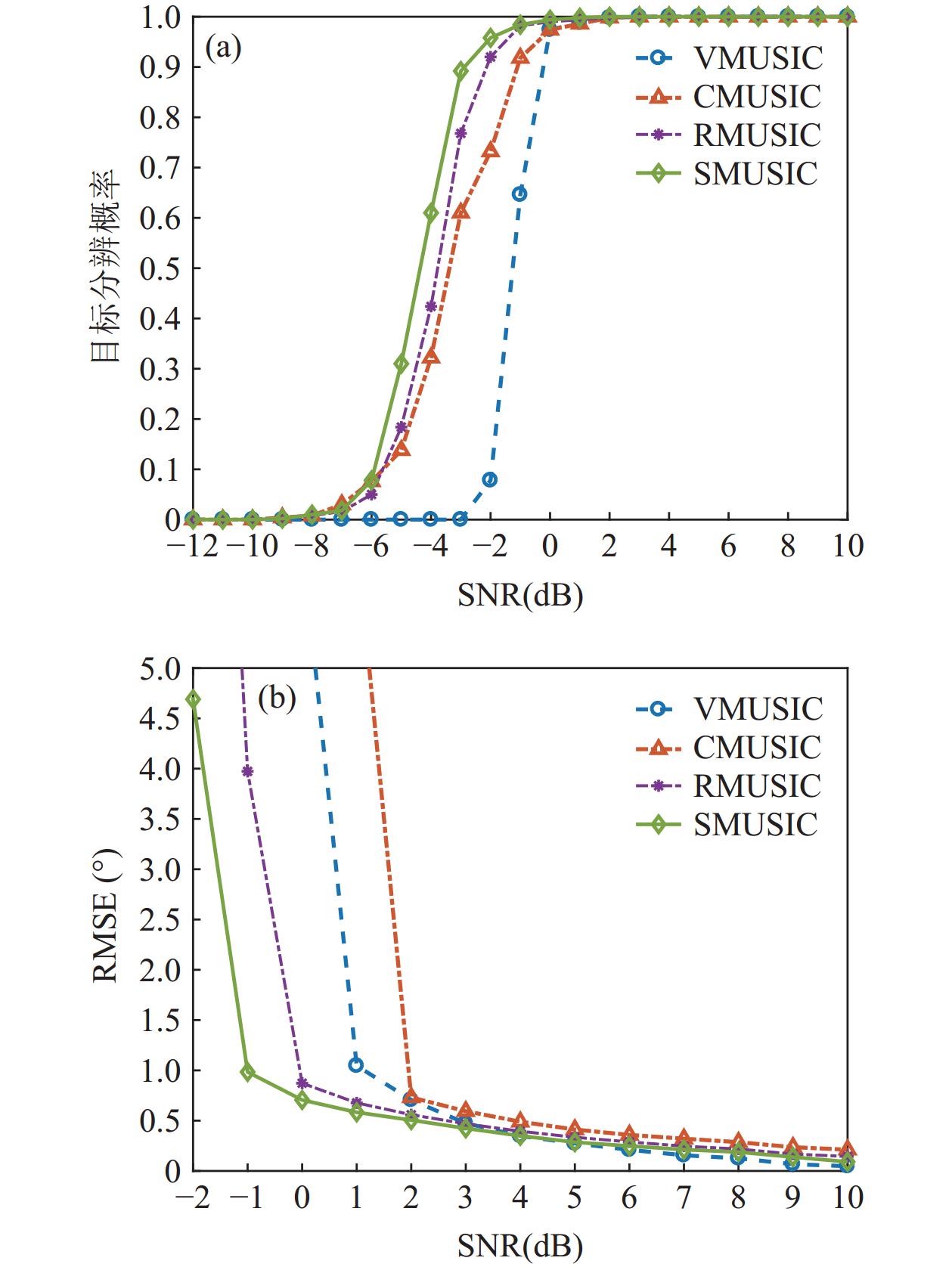
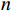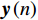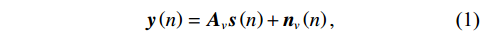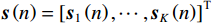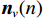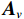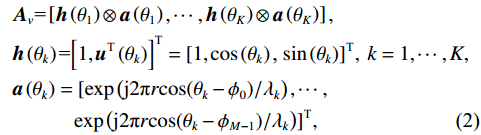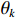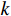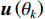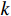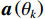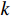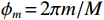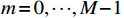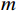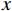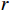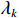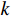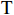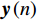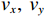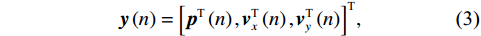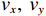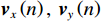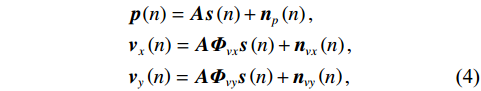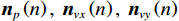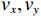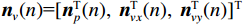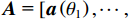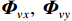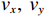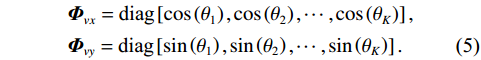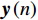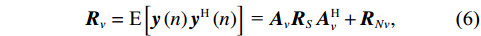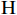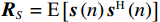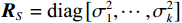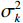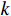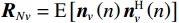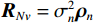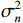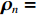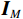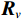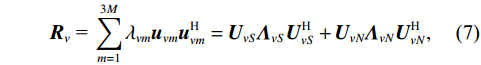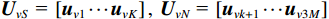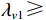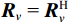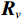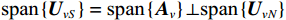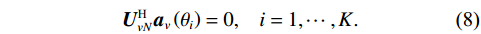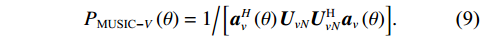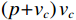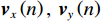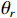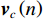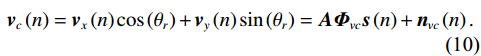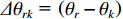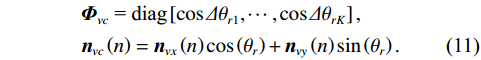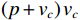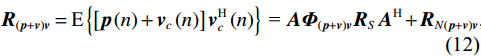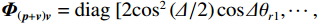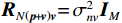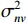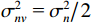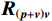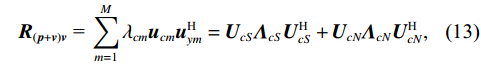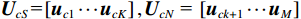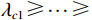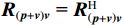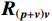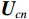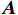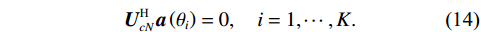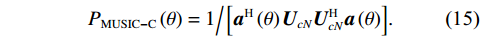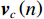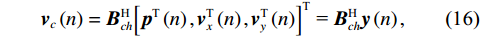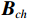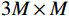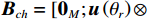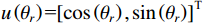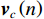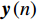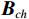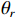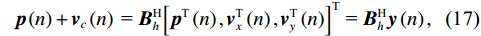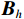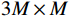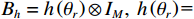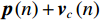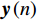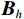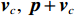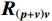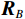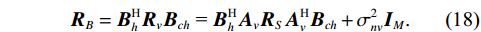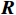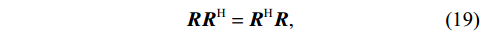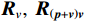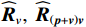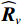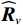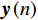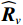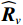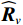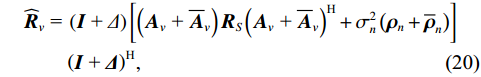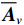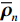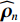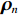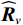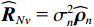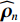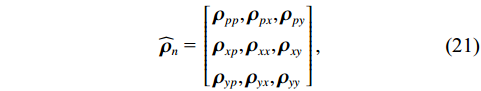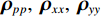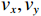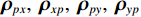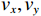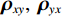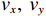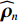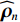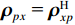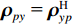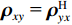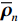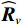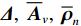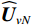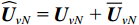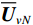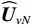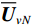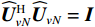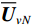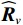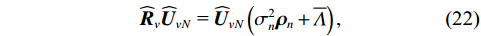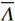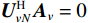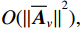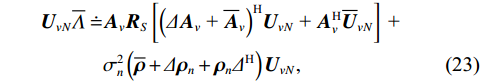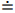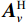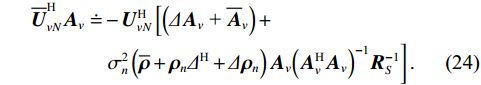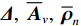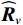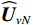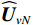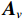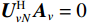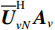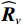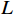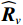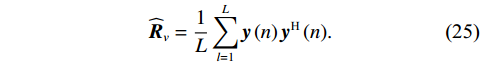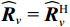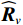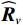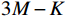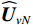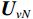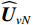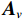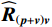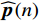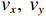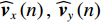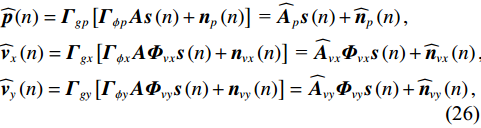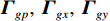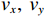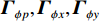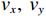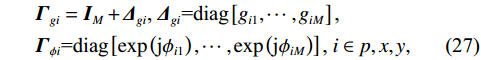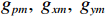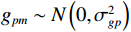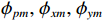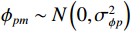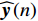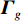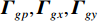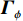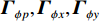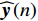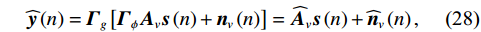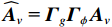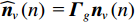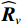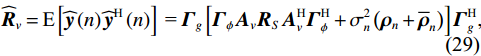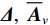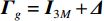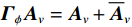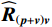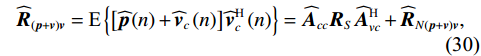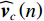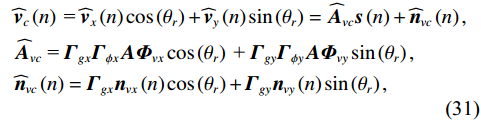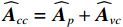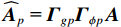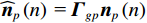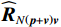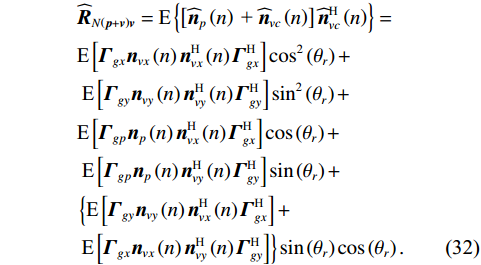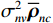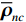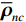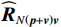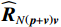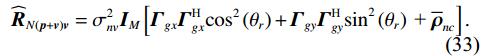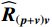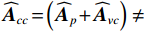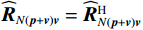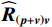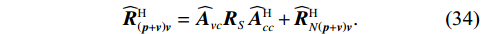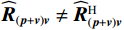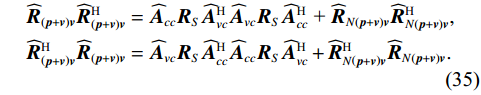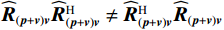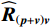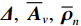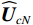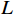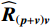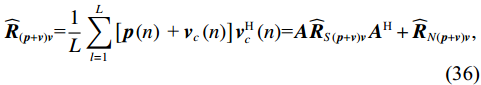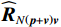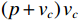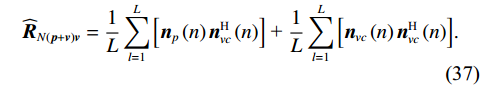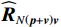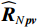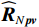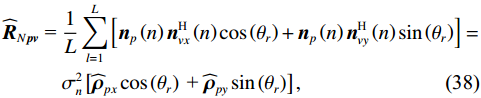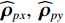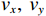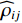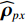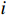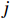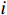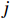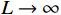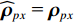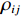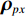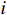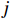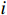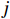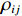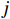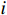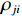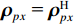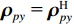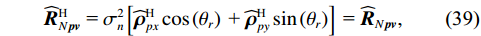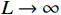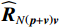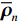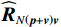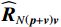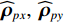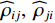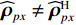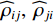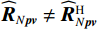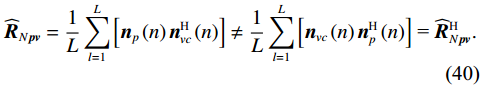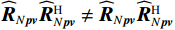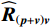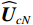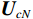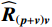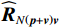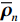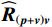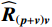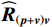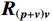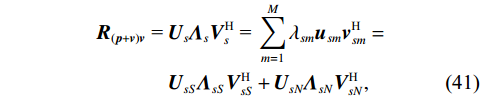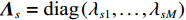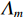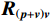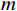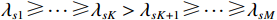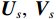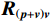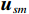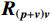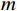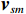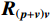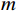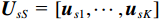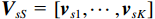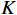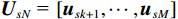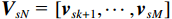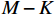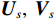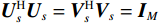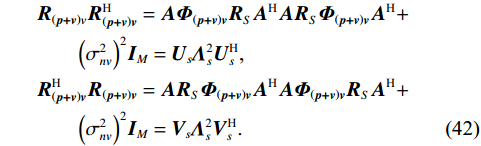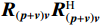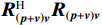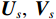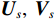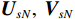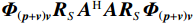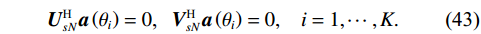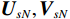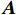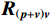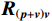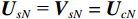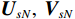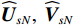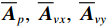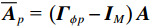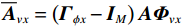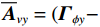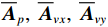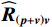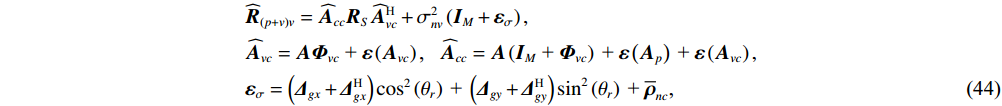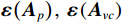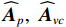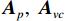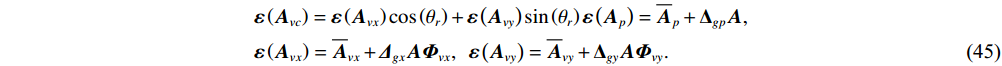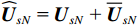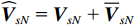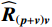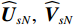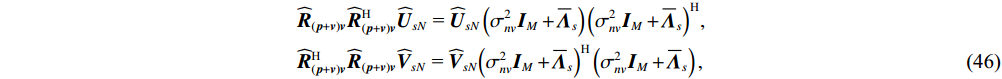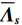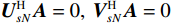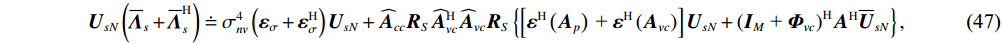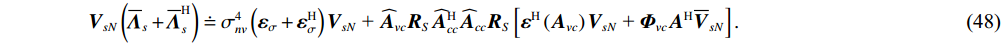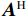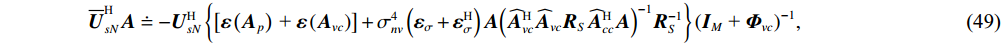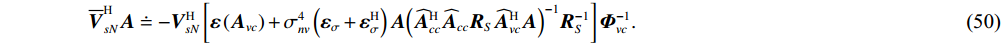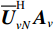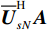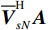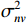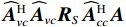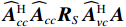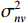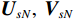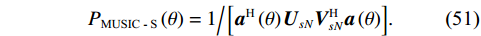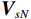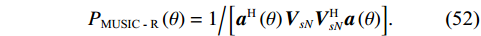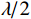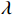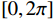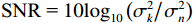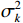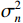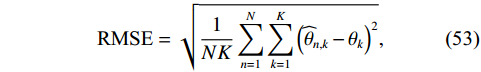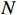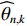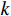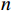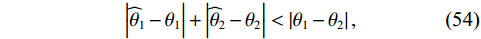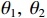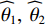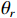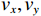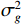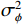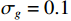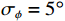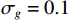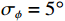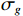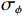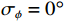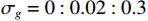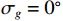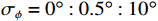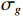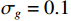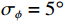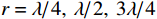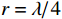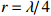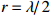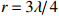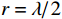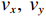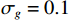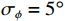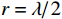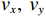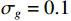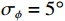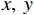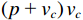An improved multiple signal classification method for a circular acoustic vector sensor array in the presence of model errors
-
摘要:
针对非正规协方差矩阵引起声矢量圆阵多重信号分类(MUSIC)测向算法性能恶化的问题, 提出了一种基于奇异值分解的声压振速联合处理MUSIC改进算法。理论分析了阵列响应误差和噪声模型误差对协方差矩阵的正规性及估计性能的影响。模型误差条件下声矢量阵声压振速联合处理的协方差矩阵不再是正规矩阵, 改进的MUSIC方法通过对声压振速联合处理的协方差矩阵进行奇异值分解, 利用非正规矩阵的左、右奇异向量自身正交的特性, 采用奇异向量张成噪声子空间。数值仿真结果表明, 改进的MUSIC方法改善了波达方向估计精度和多目标分辨能力, 且具有更低、更平坦的空间背景谱。湖上试验进一步验证了改进的MUSIC方法的有效性。
Abstract:Aiming at the problem that the direction-of-arrival (DOA) estimation performance of multiple signal classification (MUSIC) algorithm of acoustic vector sensor (AVS) uniform circular array is deteriorated by the non-normal covariance matrix, an improved MUSIC algorithm based on singular value decomposition (SVD) of combined processing method of pressure and particle velocity (PV-CPM) is proposed. The influence of array response error and noise model error on the normality of covariance matrix and the estimation performance is analyzed. The covariance matrix of AVS array is no longer a normal matrix under the condition of model error. By using SVD of the covariance matrix for PV-CPM, the singular vectors are used to span the noise subspace based on the orthogonality of the singular vectors of the non-normal matrix. Numerical simulation results show that the proposed method improves the DOA estimation accuracy and multi-target resolution ability with a lower and flatter spatial background. The lake experiment further verifies the effectiveness of the proposed method.
-
引言
近年来, 声矢量传感器阵列(以下简称声矢量阵)的波达方向(DOA)估计已取得诸多成果[1-3], 其中基于声压振速联合处理[4-8]的高分辨DOA估计方法尤其受关注。多重信号分类(MUSIC)测向方法是一种经典的子空间类高分辨算法[9]。已有研究成果表明, 与Nehorai传统处理方式[10]相比, 基于声压振速联合处理的声矢量阵MUSIC方法的信噪比门限更低、多目标分辨力更优。
理论上, 声矢量阵MUSIC方法需获得精确的阵列响应与背景噪声场二阶空间统计量的先验知识[11]。但在实际工程应用中声矢量阵列响应受阵列响应误差[12](如互耦、振速轴向不一致、阵元位置误差、各通道幅相误差等)影响, 偏离其理想假设值; 此外, 应用MUSIC方法时, 通常假设噪声场为理想情况, 再对协方差矩阵作特征值分解, 但时空变噪声[13]和有限的快拍数都可能使噪声协方差矩阵估计值与理想假设值存在偏差。信噪比(SNR)较高时, 实际噪声与理想假设的偏差对阵列协方差矩阵的估计影响不大, 但低信噪比下的影响显著。实际情况中声矢量阵的阵列响应和噪声协方差矩阵与理想假设值是失配的, 产生的模型误差会影响协方差矩阵的正规性及估计性能, 进而导致声矢量阵MUSIC方法性能恶化。
协方差矩阵的正规性[14]是声矢量阵MUSIC方法中信号子空间与噪声子空间正交的前提。Nehorai传统处理方式的协方差矩阵是接收数据的自协方差矩阵(Hermite矩阵), 属于正规矩阵, 但声压振速联合处理的协方差矩阵是声压与振速分量不同组合输出之间的互协方差矩阵。由于模型误差对声压、振速影响程度不同, 该互协方差矩阵是非对称、非正规的。非正规矩阵的各特征向量线性相关, 利用该协方差矩阵估计的信号子空间与噪声子空间之间的正交性难以保证, 导致存在模型误差时声压振速联合处理MUSIC方法性能恶化。
基于协方差矩阵正规假设, 模型误差对MUSIC方位估计性能的影响已有大量研究。文献[15]基于一阶误差方法重点分析了多种模型误差对噪声子空间的扰动, 给出了MUSIC方位估计均方误差理论表达式; 文献[16]的研究表明有限快拍数导致MUSIC方法估计偏差大于标准偏差, 引起测向精度和分辨率损失; 文献[17]推导了有限快拍偏差的严格表达式; 文献[18]利用二阶误差统计分析方法量化了阵列幅相误差下MUSIC方位估计偏差和均方误差; 文献[19]给出了阵列响应误差和噪声协方差失配情况下, MUSIC方法角度分辨率阈值的解析表达式。得益于和声压阵相似的处理框架, 这些分析结论可以扩展至Nehorai传统处理方式的声矢量阵MUSIC方法中。但研究基于声压振速联合处理的MUSIC方法时, 模型误差对协方差矩阵正规性的影响尚未引起关注。
针对上述问题, 考虑到均匀圆阵具有360°无模糊测向能力及近似相同的角度分辨力[20], 本文以声矢量均匀圆阵为研究对象, 理论分析了不同模型误差情况下声压振速联合处理协方差矩阵非正规性的产生原因, 并提出了基于奇异值分解的声压振速联合处理MUSIC改进方法。该方法根据协方差矩阵的左、右奇异向量自身相互正交的特性[21], 利用奇异向量张成噪声子空间, 改善了传统声压振速联合处理MUSIC方法的方位估计精度和多目标分辨力。数值仿真和湖试数据处理结果验证了改进的MUSIC方法的有效性。
1. 理想假设下的声矢量均匀圆阵MUSIC方法
1.1 Nehorai传统声矢量阵MUSIC方法
建立声矢量均匀圆阵阵列信号模型。考虑水下远距离目标情况, 忽略振速垂直方向分量。假设
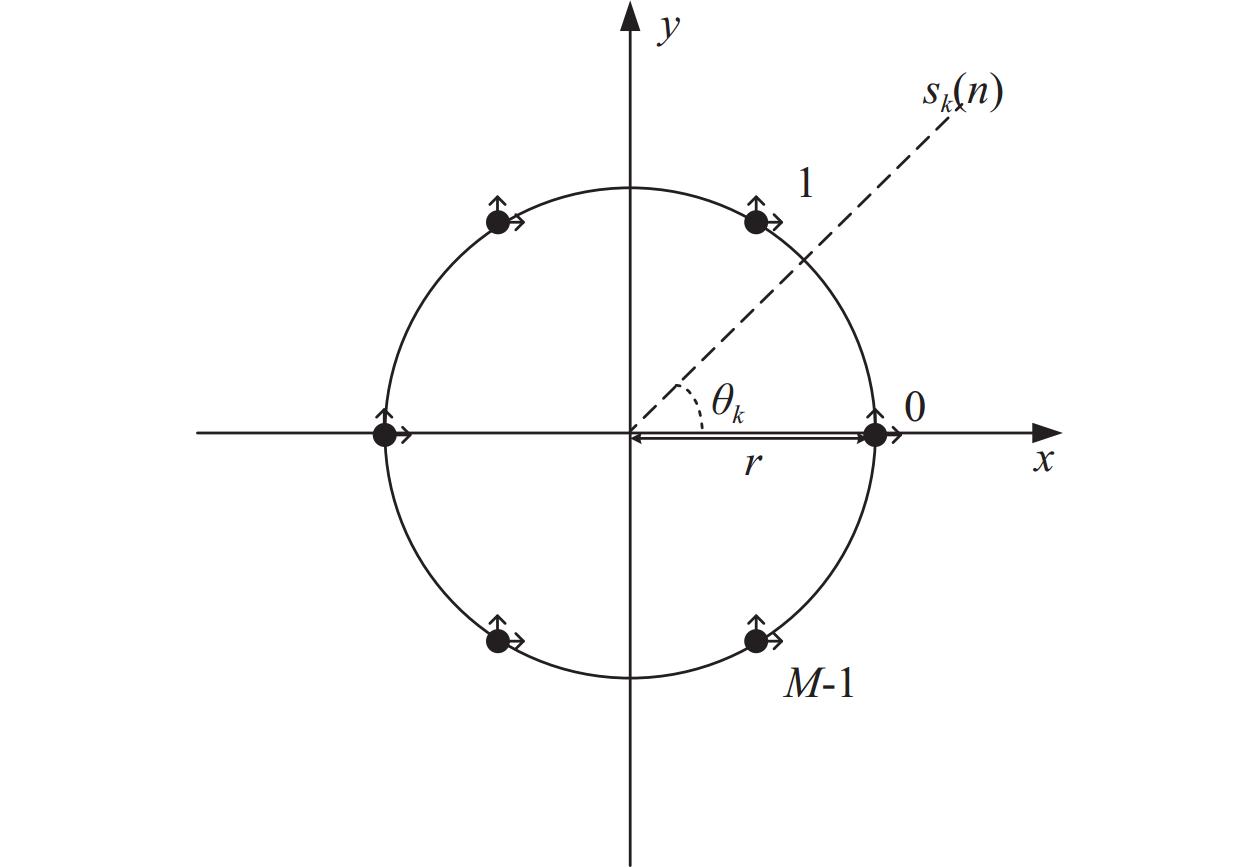
K 个不相关的远场窄带信源入射到M 元声矢量均匀圆阵上, 以矢量圆阵中心位置为参考点, 建立xOy 参考直角坐标系, 振速vx,vy 通道分别朝向x,y 轴正向, 如图1所示。声矢量均匀圆阵第
n 次快拍输出{\boldsymbol{y}}\left( n \right) 可表示为{\boldsymbol{y}}\left( n \right) = {{\boldsymbol{A}}_v}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_v}\left( n \right), (1) 式中,
{\boldsymbol{s}}\left( n \right) = {\left[ {{{\boldsymbol{s}}_1}\left( n \right), \cdots ,{{\boldsymbol{s}}_K}\left( n \right)} \right]^{\text{T}}} 为信源矢量;{{\boldsymbol{n}}_v}(n) 为各通道噪声矢量, 本节对噪声作如下理想假设: 假设噪声场是各向同性的, 阵列接收的噪声均为零均值平稳高斯过程, 各通道接收噪声互不相关, 信号与噪声也互不相关;{{\boldsymbol{A}}_v} 为声矢量阵列流形, 有\begin{split}& {{\boldsymbol{A}}}_{v}\text=\left[{\boldsymbol{h}}\left({\theta }_{1}\right)\otimes {\boldsymbol{a}}\left({\theta }_{1}\right),\cdots ,{\boldsymbol{h}}\left({\theta }_{K}\right)\otimes {\boldsymbol{a}}\left({\theta }_{K}\right)\right],\\& {\boldsymbol{h}}\left({\theta }_{k}\right)\text={\left[1,{{\boldsymbol{u}}}^{\text{T}}\left({\theta }_{k}\right)\right]}^{\text{T}}={\left[1,\mathrm{cos}\left({\theta }_{k}\right)\text{, }\mathrm{sin}\left({\theta }_{k}\right)\right]}^{\text{T}},\text{ }k=1,\cdots ,K,\\& {\boldsymbol{a}}\left({\theta }_{k}\right)=[\mathrm{exp}\left(\text{j}2\text{π}r\mathrm{cos}({\theta }_{k}-{\phi }_{0})/{\lambda }_{k}\right),\cdots ,\\&\qquad \quad \mathrm{exp}\left(\text{j}2\text{π}r\mathrm{cos}({\theta }_{k}-{\phi }_{M-1})/{\lambda }_{k}\right)]^{\text{T}},\\[-1pt] \end{split} (2) 其中,
{\theta _k} 为信源入射角, 定义为第k 个信源与x 轴正向的夹角;{\boldsymbol{u}}\left( {{\theta _k}} \right) 为第k 个信源的方向矢量;{\boldsymbol{a}}\left( {{\theta _k}} \right) 为第k 个信源的导向矢量;{\phi _m} = {2\pi m}/M (m = 0, \cdots , M - 1 )表示第m 个阵元与x 轴正向的夹角;r 为圆阵半径;{\lambda _k} 为第k 个信源波长; 符号\otimes 表示克罗内克积, 符号{\text{T}} 表示转置。{\boldsymbol{y}}\left( n \right) 可具体表示为声压通道和振速{v_x},{\text{ }}{v_y} 通道的输出矢量的形式:{\boldsymbol{y}}\left( n \right) = {\left[ {{{\boldsymbol{p}}^{\text{T}}}\left( n \right),{\boldsymbol{v}}_x^{\text{T}}\left( n \right),{\boldsymbol{v}}_y^{\text{T}}\left( n \right)} \right]^{\text{T}}}, (3) 式中, 声压通道输出矢量
{\boldsymbol{p}}\left( n \right) 和振速{v_x},{\text{ }}{v_y} 通道输出矢量{{\boldsymbol{v}}_x}\left( n \right),{\text{ }}{{\boldsymbol{v}}_y}\left( n \right) 分别为\begin{split}& {\boldsymbol{p}}\left( n \right) = {\boldsymbol{As}}\left( n \right) + {{\boldsymbol{n}}_p}\left( n \right), \\& {{\boldsymbol{v}}_x}\left( n \right) = {\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{vx}}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_{vx}}\left( n \right), \\& {{\boldsymbol{v}}_y}\left( n \right) = {\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{vy}}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_{vy}}\left( n \right), \end{split} (4) 式中,
{{\boldsymbol{n}}_p}\left( n \right),{\text{ }}{{\boldsymbol{n}}_{vx}}\left( n \right),{\text{ }}{{\boldsymbol{n}}_{vy}}\left( n \right) 为声压和振速{v_x},{v_y} 通道噪声矢量, 有{{\boldsymbol{n}}_v}(n){\text{=}}{[ {{\boldsymbol{n}}_p^{\text{T}}(n),{\text{ }}{\boldsymbol{n}}_{vx}^{\text{T}}(n),{\text{ }}{\boldsymbol{n}}_{vy}^{\text{T}}(n)} ]^{\text{T}}} ;{\boldsymbol{A}}{\text{ = }}[ {\boldsymbol{a}}\left( {{\theta _1}} \right), \cdots , {\boldsymbol{a}}\left( {{\theta _K}} \right)] 为声压阵列流形矩阵;{{\boldsymbol{\varPhi }}_{vx}},{\text{ }}{{\boldsymbol{\varPhi }}_{vy}} 分别为振速{v_x},{\text{ }}{v_y} 通道系数矩阵:\begin{split}& {{\boldsymbol{\varPhi }}_{vx}} = {\text{diag}}\left[ {\cos \left( {{\theta _1}} \right),\cos \left( {{\theta _2}} \right), \cdots ,\cos \left( {{\theta _K}} \right)} \right], \\& {{\boldsymbol{\varPhi }}_{vy}} = {\text{diag}}\left[ {\sin \left( {{\theta _1}} \right),\sin \left( {{\theta _2}} \right), \cdots ,\sin \left( {{\theta _K}} \right)} \right]. \end{split} (5) Nehorai传统声矢量阵MUSIC方法利用输出矢量
{\boldsymbol{y}}\left( n \right) 估计协方差矩阵:{{\boldsymbol{R}}_v} = {\text{E}}\left[ {{\boldsymbol{y}}\left( n \right){{\boldsymbol{y}}^{\text{H}}}\left( n \right)} \right]{\text{ = }}{{\boldsymbol{A}}_v}{{\boldsymbol{R}}_S}{\boldsymbol{A}}_v^{\text{H}} + {{\boldsymbol{R}}_{Nv}}, (6) 式中, 符号
{\text{H}} 表示共轭转置运算;{{\boldsymbol{R}}_S} = {\text{E}}\left[ {{\boldsymbol{s}}\left( n \right){{\boldsymbol{s}}^{\text{H}}}\left( n \right)} \right] 为信号协方差矩阵,{{\boldsymbol{R}}_S} = {\text{diag}}\left[ {\sigma _1^2, \cdots ,\sigma _k^2} \right] ,\sigma _k^2 为第k 个信源功率;{{\boldsymbol{R}}_{Nv}} = {\text{E}}\left[ {{{\boldsymbol{n}}_v}\left( n \right){\boldsymbol{n}}_v^{\text{H}}\left( n \right)} \right] 为噪声协方差矩阵, 有{{\boldsymbol{R}}_{Nv}} = \sigma _n^2{{\boldsymbol{\rho }}_n} ,\sigma _n^2 为声压通道的噪声功率,{{\boldsymbol{\rho }}_n} = {\text{diag}}\left[ {1,{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2},{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}} \right] \otimes {{\boldsymbol{I}}_M} 为归一化噪声协方差矩阵,{{\boldsymbol{I}}_M} 为M \times M 维零矩阵。对协方差矩阵
{{\boldsymbol{R}}_v} 进行特征值分解:{{\boldsymbol{R}}_v}{\text{ = }}\sum\limits_{m = 1}^{3M} {{\lambda _{vm}}{{\boldsymbol{u}}_{vm}}{\boldsymbol{u}}_{vm}^{\text{H}}} = {{\boldsymbol{U}}_{vS}}{{\boldsymbol{\varLambda }}_{vS}}{\boldsymbol{U}}_{vS}^{\text{H}} + {{\boldsymbol{U}}_{vN}}{{\boldsymbol{\varLambda }}_{vN}}{\boldsymbol{U}}_{vN}^{\text{H}}, (7) 式中,
{{\boldsymbol{U}}_{vS}}{\text{ = }}\left[ {{{\boldsymbol{u}}_{v1}} \cdots {{\boldsymbol{u}}_{vK}}} \right],{\text{ }}{{\boldsymbol{U}}_{vN}}{\text{ = }}\left[ {{{\boldsymbol{u}}_{vk + 1}} \cdots {{\boldsymbol{u}}_{v3M}}} \right] , 且{\lambda _{v1}} \geqslant \cdots \geqslant{\lambda _{vK}} > {\lambda _{vK + 1}} \geqslant \cdots \geqslant {\lambda _{v3M}} 。根据式(6), 显然有
{{\boldsymbol{R}}_v}{\text{ = }}{\boldsymbol{R}}_v^{\text{H}} ,{{\boldsymbol{R}}_v} 为Hermite矩阵, 其不同特征值的特征子空间互相正交。因此有{\text{span}}\left\{ {{{\boldsymbol{U}}_{vS}}} \right\} = {\text{span}}\left\{ {{{\boldsymbol{A}}_v}} \right\} \bot {\text{span}}\left\{ {{{\boldsymbol{U}}_{vN}}} \right\} , 则\begin{array}{*{20}{c}} {{\boldsymbol{U}}_{vN}^{\text{H}}{{\boldsymbol{a}}_v}\left( {{\theta _i}} \right) = 0,}&{i = 1, \cdots ,K} . \end{array} (8) 得到Nehorai传统声矢量阵MUSIC空间谱函数:
{P_{{\text{MUSIC}} - V}}\left( \theta \right) = {1 \mathord{\left/ {\vphantom {1 {\left[ {{\boldsymbol{a}}_v^H\left( \theta \right){{\boldsymbol{U}}_{vN}}{\boldsymbol{U}}_{vN}^{\text{H}}{{\boldsymbol{a}}_v}\left( \theta \right)} \right]}}} \right. } {\left[ {{\boldsymbol{a}}_v^H\left( \theta \right){{\boldsymbol{U}}_{vN}}{\boldsymbol{U}}_{vN}^{\text{H}}{{\boldsymbol{a}}_v}\left( \theta \right)} \right]}}. (9) 1.2 声压振速联合处理MUSIC方法
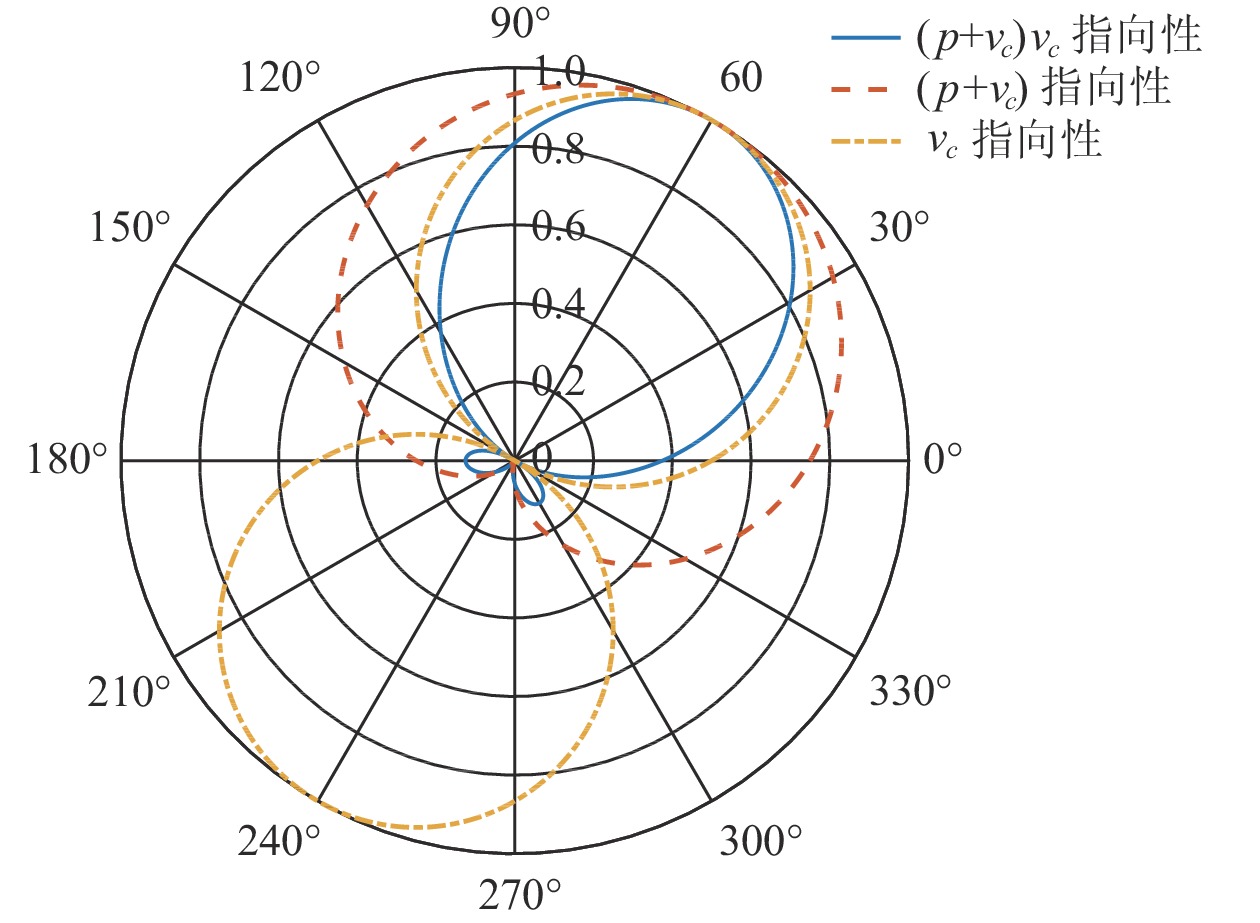
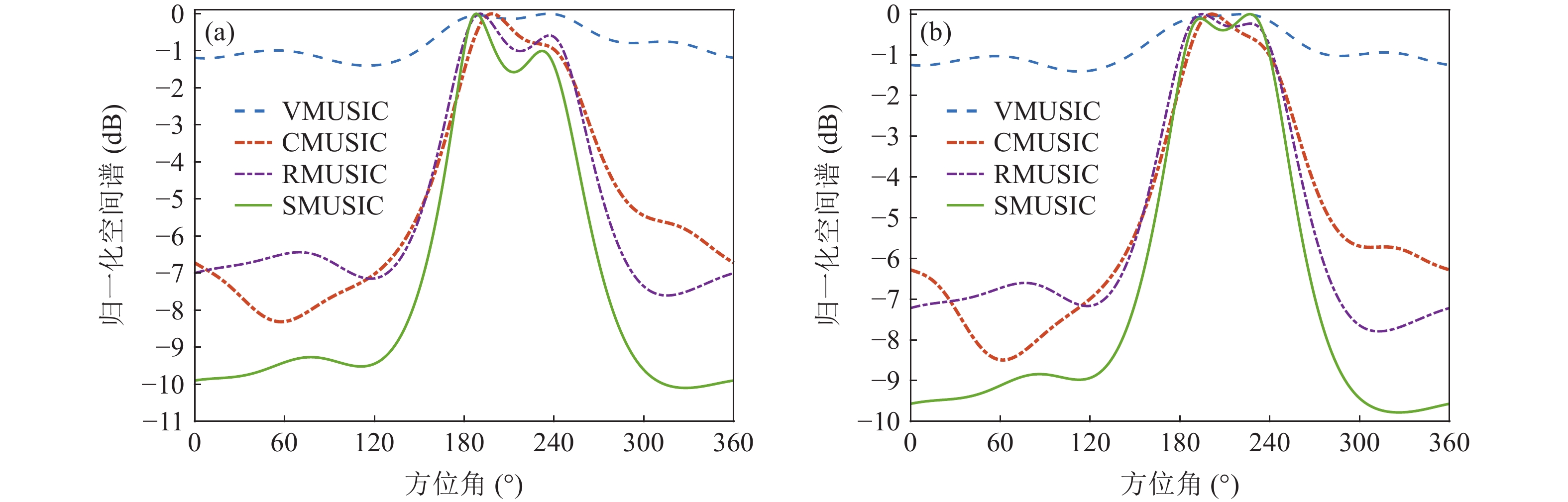
声矢量阵声压振速联合处理可利用声压振速组合指向性抑制噪声和干扰。选取具有较高的组合指向性增益[22]的
\left( {p + {v_c}} \right){v_c} 组合形式, 其指向性见图2。将振速分量
{{\boldsymbol{v}}_x}\left( n \right),{\text{ }}{{\boldsymbol{v}}_y}\left( n \right) 向某观测方位{\theta _r} 上投影, 得到组合振速{{\boldsymbol{v}}_c}\left( n \right) :{{\boldsymbol{v}}_c}\left( n \right) = {{\boldsymbol{v}}_x}\left( n \right)\cos \left( {{\theta _r}} \right) + {{\boldsymbol{v}}_y}\left( n \right)\sin \left( {{\theta _r}} \right) = {\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{vc}}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_{vc}}\left( n \right). (10) 令
\varDelta {\theta _{rk}}{\text{ = }}\left( {{\theta _r} - {\theta _k}} \right) , 则\begin{split} & {{\boldsymbol{\varPhi }}_{vc}}{\text{ = diag}}\left[ {\cos \varDelta {\theta _{r1}}, \cdots ,\cos \varDelta {\theta _{rK}}} \right], \\& {{\boldsymbol{n}}_{vc}}\left( n \right) = {{\boldsymbol{n}}_{vx}}\left( n \right)\cos \left( {{\theta _r}} \right) + {{\boldsymbol{n}}_{vy}}\left( n \right)\sin \left( {{\theta _r}} \right). \end{split} (11) 获取
\left( {p + {v_c}} \right){v_c} 组合形式的声压振速互协方差矩阵:{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = {\text{E}}\left\{ {\left[ {{\boldsymbol{p}}\left( n \right) + {{\boldsymbol{v}}_c}\left( n \right)} \right]{\boldsymbol{v}}_c^{\text{H}}\left( n \right)} \right\}{\text{ = }}{\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{{\boldsymbol{R}}_S}{{\boldsymbol{A}}^{\text{H}}} + {{\boldsymbol{R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}, (12) 式中, 系数矩阵
{{\boldsymbol{\varPhi }}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = {\rm diag}\;[ 2{{\cos }^2}\left( {\varDelta / 2} \right)\cos \varDelta {\theta _{r1}}, \cdots , 2{{\cos }^2}\left( {{\varDelta {\theta _{rK}}} / 2} \right)\cos \varDelta {\theta _{rK}} ] ; 噪声协方差矩阵{{\boldsymbol{R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = \sigma _{nv}^2{{\boldsymbol{I}}_M} ,\sigma _{nv}^2 为振速通道噪声功率, 有\sigma _{nv}^2{\text{ = }}{{\sigma _n^2} \mathord{\left/ {\vphantom {{\sigma _n^2} 2}} \right. } 2} 。对
{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 进行特征值分解:{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{\text{ = }}\sum\limits_{m = 1}^M {{\lambda _{cm}}{{\boldsymbol{u}}_{cm}}{\boldsymbol{u}}_{ym}^{\text{H}}} = {{\boldsymbol{U}}_{cS}}{{\boldsymbol{\varLambda }}_{cS}}{\boldsymbol{U}}_{cS}^{\text{H}} + {{\boldsymbol{U}}_{cN}}{{\boldsymbol{\varLambda }}_{cN}}{\boldsymbol{U}}_{cN}^{\text{H}}, (13) 式中,
{{\boldsymbol{U}}_{cS}}{\text{=}}\left[ {{{\boldsymbol{u}}_{c1}} \cdots {{\boldsymbol{u}}_{cK}}} \right],{{\boldsymbol{U}}_{cN}}{\text{ = }}\left[ {{{\boldsymbol{u}}_{ck + 1}} \cdots {{\boldsymbol{u}}_M}} \right] , 且{\lambda _{c1}} \geqslant \cdots \geqslant {\lambda _{cK}} > {\lambda _{cK + 1}} \geqslant \cdots \geqslant {\lambda _{cM}} 。根据式(12), 有
{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{\text{ = }}{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}} , 协方差矩阵{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 为Hermite矩阵, 其噪声子空间{{\boldsymbol{U}}_{cn}} 与导向矢量{\boldsymbol{A}} 满足{{\boldsymbol{U}}_{cN}^{\text{H}}{\boldsymbol{a}}\left( {{\theta _i}} \right) = 0},\quad {i = 1, \cdots ,K} . (14) 得到基于声压振速联合处理的声矢量阵MUSIC空间谱函数:
{P_{\rm MUSIC - C}}\left( \theta \right) = {1 \mathord{\left/ {\vphantom {1 {\left[ {{{\boldsymbol{a}}^{\text{H}}}\left( \theta \right){{\boldsymbol{U}}_{cN}}{\boldsymbol{U}}_{cN}^{\text{H}}{\boldsymbol{a}}\left( \theta \right)} \right]}}} \right. } {\left[ {{{\boldsymbol{a}}^{\text{H}}}\left( \theta \right){{\boldsymbol{U}}_{cN}}{\boldsymbol{U}}_{cN}^{\text{H}}{\boldsymbol{a}}\left( \theta \right)} \right]}}. (15) 1.3 方法性能理论分析
重写声压振速联合处理中组合振速
{{\boldsymbol{v}}_c}\left( n \right) 的表达式:{{\boldsymbol{v}}_c}\left( n \right) = {\boldsymbol{B}}_{ch}^{\text{H}}{\left[ {{{\boldsymbol{p}}^{\text{T}}}\left( n \right),{\boldsymbol{v}}_x^{\text{T}}\left( n \right),{\boldsymbol{v}}_y^{\text{T}}\left( n \right)} \right]^{\text{T}}}{\text{ = }}{\boldsymbol{B}}_{ch}^{\text{H}}{\boldsymbol{y}}\left( n \right), (16) 式中,
{{\boldsymbol{B}}_{ch}} 是3M \times M 维变换矩阵,{{\boldsymbol{B}}_{ch}} = [ {\boldsymbol{0}}_M; \boldsymbol{u}\left( {{\theta _r}} \right) \otimes {{\boldsymbol{I}}_M} ] ,u\left({\theta }_{r}\right)\text{=}{\left[\mathrm{cos}\left({\theta }_{r}\right), \mathrm{sin}\left({\theta }_{r}\right)\right]}^{\text{T}} , 即组合振速{{\boldsymbol{v}}_c}\left( n \right) 实质上是由接收数据{\boldsymbol{y}}\left( n \right) 经波束变换矩阵{{\boldsymbol{B}}_{ch}} 处理后得到的指向{\theta _r} 的波束域数据。同理, 有{\boldsymbol{p}}\left( n \right) + {{\boldsymbol{v}}_c}\left( n \right){\text{ = }}{\boldsymbol{B}}_h^{\text{H}}{\left[ {{{\boldsymbol{p}}^{\text{T}}}\left( n \right),{\boldsymbol{v}}_x^{\text{T}}\left( n \right),{\boldsymbol{v}}_y^{\text{T}}\left( n \right)} \right]^{\text{T}}}{\text{ = }}{\boldsymbol{B}}_h^{\text{H}}{\boldsymbol{y}}\left( n \right), (17) 式中,
{{\boldsymbol{B}}_h} 是3M \times M 维变换矩阵,{B}_{h} = h\left({\theta }_{r}\right)\otimes {I}_{M}, ~ h\left({\theta }_{r}\right)\text{=} {\left[1,\mathrm{cos}\left({\theta }_{r}\right), \mathrm{sin}\left({\theta }_{r}\right)\right]}^{\text{T}} 。{\boldsymbol{p}}\left( n \right) + {{\boldsymbol{v}}_c}\left( n \right) 是{\boldsymbol{y}}\left( n \right) 经波束变换矩阵{{\boldsymbol{B}}_h} 处理得到的波束域数据。{{\boldsymbol{v}}_c},{\text{ }}{\boldsymbol{p}} + {{\boldsymbol{v}}_c} 的指向性见图2。声压振速联合处理预先利用不同的波束变换矩阵分别形成具有不同指向性的波束域数据, 再利用波束域数据的互协方差矩阵进行DOA估计。将式(16)和式(17)代入式(12), 可得
{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 的另一表达形式{{\boldsymbol{R}}_B} :{{\boldsymbol{R}}_B} = {\boldsymbol{B}}_h^{\text{H}}{{\boldsymbol{R}}_v}{{\boldsymbol{B}}_{ch}}{\text{ = }}{\boldsymbol{B}}_h^{\text{H}}{{\boldsymbol{A}}_v}{{\boldsymbol{R}}_S}{\boldsymbol{A}}_v^{\text{H}}{{\boldsymbol{B}}_{ch}} + \sigma _{nv}^2{{\boldsymbol{I}}_M}. (18) 可见, 基于声压振速联合处理的声矢量阵MUSIC方法实质上是一种特殊的波束域MUSIC方位估计方法, Nehorai传统声矢量阵MUSIC方法为其对应的阵元域MUSIC方法。因此, 可直接利用阵元域与波束域MUSIC方法的结论分析Nehorai传统声矢量阵MUSIC方法和声压振速联合处理MUSIC方法的性能。文献[23]表明, 阵元域MUSIC方法的方位角度估计精度优于波束域MUSIC方法, 但根据文献[24]的相关研究, 波束域MUSIC方法的优势在于: (1) 增强对两方位相近信源的分辨能力; (2) 增强对更低信噪比目标的检测能力; (3) 降低算法复杂度。
2. 模型误差下的声矢量均匀圆阵MUSIC方法
2.1 存在模型误差的Nehorai传统声矢量阵协方差矩阵
MUSIC方法基于信号子空间与噪声子空间的正交性, 即协方差矩阵不同特征值对应的特征子空间相互正交。因此要求协方差矩阵
{\boldsymbol{R}} 为正规矩阵:{\boldsymbol{R}}{{\boldsymbol{R}}^{\text{H}}} = {{\boldsymbol{R}}^{\text{H}}}{\boldsymbol{R}}, (19) 显然, 第1节理想假设下
{{\boldsymbol{R}}_v},{\text{ }}{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 为Hermite矩阵, 均满足该要求。但模型误差条件下, 协方差矩阵{{\boldsymbol{\widehat R}}_v},{\text{ }}{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 的正规性和估计性能均可能发生改变。将影响协方差矩阵的模型误差分为两类: 一类是阵列响应误差和噪声协方差误差等系统误差, 可直接以误差项的形式写入误差条件下的协方差矩阵模型中; 另一类是有限快拍数、低信噪比等影响协方差矩阵估计性能的估计误差。本节分析两类模型误差对Nehorai传统声矢量阵MUSIC方法协方差矩阵
{{\boldsymbol{\widehat R}}_v} 的影响, 并给出系统误差对噪声子空间的扰动。模型误差影响下,
{{\boldsymbol{\widehat R}}_v} 仍是{\boldsymbol{y}}\left( n \right) 的自协方差矩阵, 为Hermite矩阵, 满足正规性条件。系统误差条件下的{{\boldsymbol{\widehat R}}_v} 可用模型误差条件下的一般化模型[15]表示。忽略有限快拍数等估计误差影响, 假设协方差矩阵{{\boldsymbol{\widehat R}}_v} 能够精确测量, 那么{{\boldsymbol{\widehat R}}_v} 的一般化模型为\begin{split} {{{\widehat {\boldsymbol{R}}}}_v}{\text{ = }}&\left( {{\boldsymbol{I}}{\text{ + }}\varDelta } \right)\left[ {\left( {{{\boldsymbol{A}}_v}{\text{ + }}{{{{\overline {\boldsymbol{A}}}}}_v}} \right){{\boldsymbol{R}}_S}{{\left( {{{\boldsymbol{A}}_v}{\text{ + }}{{{{\overline {\boldsymbol{A}}}}}_v}} \right)}^{\text{H}}} + \sigma _n^2\left( {{{\boldsymbol{\rho }}_n} + {{{{\overline {\boldsymbol{\rho}} }}}_n}} \right)} \right]\\&{\left( {{\boldsymbol{I}}{\text{ + }}{\boldsymbol{\varDelta }}} \right)^{\text{H}}},\\[-1pt] \end{split} (20) 式中, 矩阵
\varDelta 包含同时影响信号与噪声分量的误差项, 如矢量阵各通道增益误差、信道串扰和互耦效应等; 矩阵{{{\overline {\boldsymbol A}}}_v} 包括仅影响阵列响应的误差, 如矢量阵各通道相位误差、阵元位置误差、振速轴向不一致误差等; 矩阵{{\overline{\boldsymbol \rho }}_n} 表示加性噪声统计量{{\boldsymbol{\widehat \rho }}_n} 与{{\boldsymbol{\rho }}_n} 的偏差, 定义{{\boldsymbol{\widehat R}}_v} 的噪声协方差矩阵{{\boldsymbol{\widehat R}}_{Nv}}{\text{ = }}\sigma _n^2{{\boldsymbol{\widehat \rho }}_n} ,{{\boldsymbol{\widehat \rho }}_n} 的一般形式为{{\boldsymbol{\widehat \rho }}_n}{\text{ = }}\left[ \begin{gathered} {{\boldsymbol{\rho }}_{pp}},{{\boldsymbol{\rho }}_{px}},{{\boldsymbol{\rho }}_{py}} \\ {{\boldsymbol{\rho }}_{xp}},{{\boldsymbol{\rho }}_{xx}},{{\boldsymbol{\rho }}_{xy}} \\ {{\boldsymbol{\rho }}_{yp}},{{\boldsymbol{\rho }}_{yx}},{{\boldsymbol{\rho }}_{yy}} \\ \end{gathered} \right], (21) 式中,
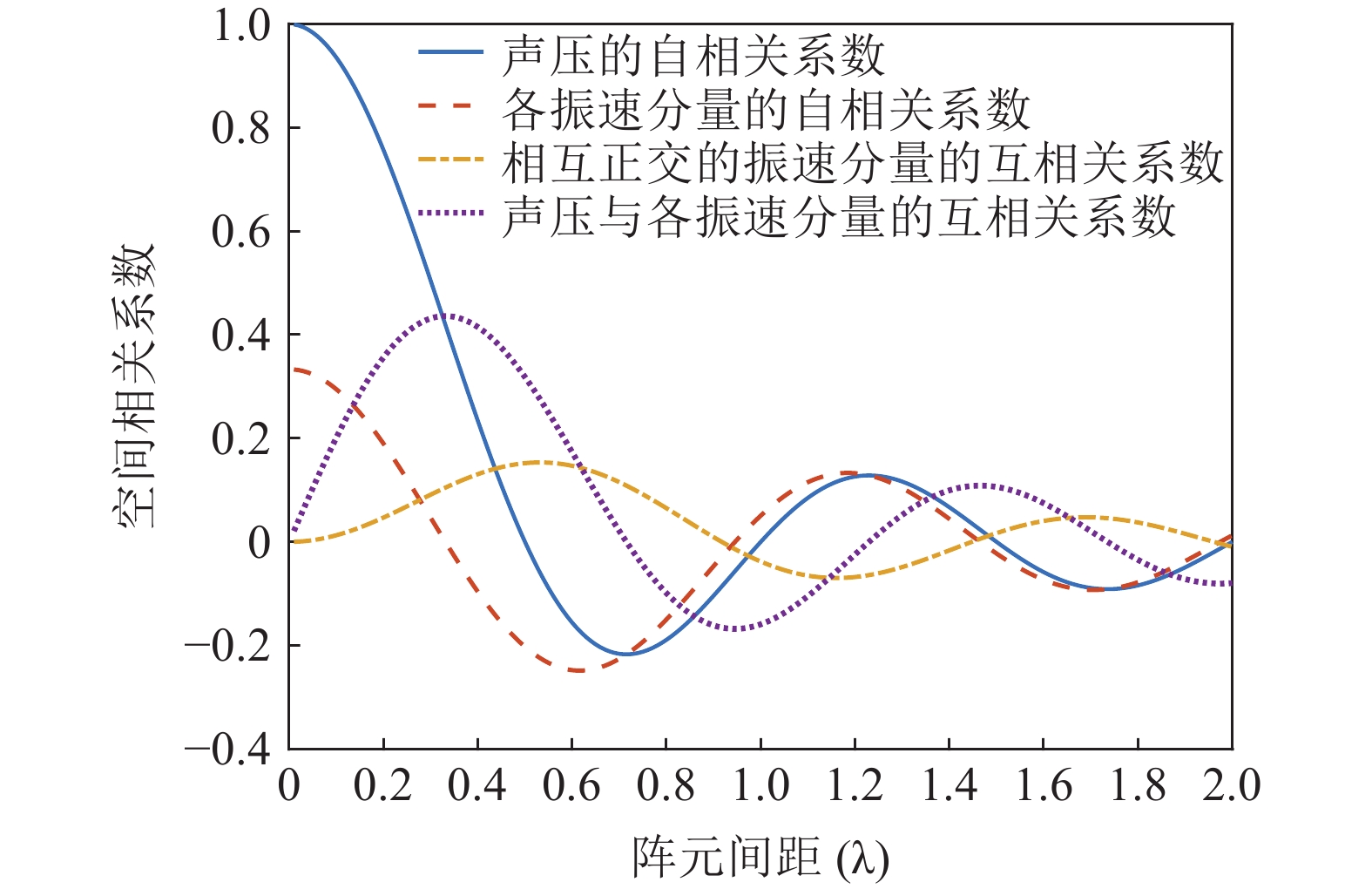
{{\boldsymbol{\rho }}_{pp}},{\text{ }}{{\boldsymbol{\rho }}_{xx}},{\text{ }}{{\boldsymbol{\rho }}_{yy}} 分别为声压通道、振速{v_x},{v_y} 通道的自相关系数矩阵;{{\boldsymbol{\rho }}_{px}},{\text{ }}{{\boldsymbol{\rho }}_{xp}},{\text{ }}{{\boldsymbol{\rho }}_{py}},{\text{ }}{{\boldsymbol{\rho }}_{yp}} 分别为声压与振速{v_x},{v_y} 通道的互相关系数矩阵;{{\boldsymbol{\rho }}_{xy}},{\text{ }}{{\boldsymbol{\rho }}_{yx}} 为振速{v_x},{\text{ }}{v_y} 通道之间的互相关系数矩阵。图3为各向同性噪声场中声压与振速的空间相关性曲线, 可见实际并不存在一阵元间距使{{\boldsymbol{\widehat \rho }}_n} 中互相关系数矩阵同时为零矩阵, 即1.1节中各通道接收噪声互不相关的假设并不成立,{{\boldsymbol{\widehat \rho }}_n} 并非对角阵。但对于互相关系数矩阵, 仍有{{\boldsymbol{\rho }}_{px}}{\text{ = }}{\boldsymbol{\rho }}_{xp}^{\text{H}} ,{{\boldsymbol{\rho }}_{py}}{\text{ = }}{\boldsymbol{\rho }}_{yp}^{\text{H}} ,{{\boldsymbol{\rho }}_{xy}}{\text{ = }}{\boldsymbol{\rho }}_{yx}^{\text{H}} , 即{{\overline{\boldsymbol \rho }}_n} 为Hermite矩阵, 这也保证了{{\boldsymbol{\widehat R}}_v} 仍为Hermite矩阵。分析模型误差对噪声子空间的扰动。假定误差矩阵
{\boldsymbol{\varDelta }},{\text{ }}{{{\overline {\boldsymbol A}}}_v},{\text{ }}{{\overline{\boldsymbol \rho }}_n} 影响下, 扰动的噪声子空间为{{\boldsymbol{\widehat U}}_{vN}} , 有{{\boldsymbol{\widehat U}}_{vN}}{\text{ = }}{{\boldsymbol{U}}_{vN}}{\text{ + }}{{\overline{\boldsymbol U}}_{vN}} , 其中,{{\overline{\boldsymbol U}}_{vN}} 为噪声子空间的扰动量。假设{{\boldsymbol{\widehat U}}_{vN}} 和{{\overline{\boldsymbol U}}_{vN}} 均被归一化, 有{\boldsymbol{\widehat U}}_{vN}^{\text{H}}{{\boldsymbol{\widehat U}}_{vN}} = {\boldsymbol{I}} 。为建立式(20)中各误差项与{{\overline{\boldsymbol U}}_{vN}} 之间的联系, 定义{{\boldsymbol{\widehat R}}_v} 的噪声子空间:{{\boldsymbol{\widehat R}}_v}{{\boldsymbol{\widehat U}}_{vN}}{\text{ = }}{{\boldsymbol{\widehat U}}_{vN}}\left( {\sigma _n^2{{\boldsymbol{\rho }}_n} + \overline \varLambda } \right), (22) 式中,
\overline \varLambda 表示扰动的噪声特征值。将式(20)代入式(22), 由{\boldsymbol{U}}_{vN}^{\text{H}}{{\boldsymbol{A}}_v} = 0 , 并且忽略二阶误差项, 例如{O}( {{{\| {{{{{\overline {\boldsymbol A}}}}_v}} \|}^2}} ), {\text{ }}{O}\left( {\left\| {{{{{\overline {\boldsymbol A}}}}_v}} \right\|\left\| {\boldsymbol{\varDelta }} \right\|} \right),{\text{ }}{O}\left( {\left\| {{{{\overline{\boldsymbol \rho }}}_n}} \right\|\left\| {\boldsymbol{\varDelta }} \right\|} \right) 等, 可得\begin{split} {{\boldsymbol{U}}_{vN}}\overline \varLambda \doteq &{{\boldsymbol{A}}_v}{{\boldsymbol{R}}_S}\left[ {{{\left( {\varDelta {{\boldsymbol{A}}_v}{\text{ + }}{{{{\overline {\boldsymbol A}}}}_v}} \right)}^{\text{H}}}{{\boldsymbol{U}}_{vN}}{\text{ + }}{\boldsymbol{A}}_v^{\text{H}}{{{\overline{\boldsymbol U}}}_{vN}}} \right]{\text{ + }}\\&\sigma _n^2\left( {{\overline{\boldsymbol \rho }} + \varDelta {{\boldsymbol{\rho }}_n} + {{\boldsymbol{\rho }}_n}{\varDelta ^{\text{H}}}} \right){{\boldsymbol{U}}_{vN}}, \end{split} (23) 式中, 符号
\doteq 表示扰动的一阶近似。式(23)两侧左乘{\boldsymbol{A}}_v^{\text{H}} , 继续化简并对等式两侧做共轭转置, 得\begin{split} {\overline{\boldsymbol U}}_{vN}^{\text{H}}{{\boldsymbol{A}}_v} \doteq & - {\boldsymbol{U}}_{vN}^{\text{H}}\left[ \left( {\varDelta {{\boldsymbol{A}}_v}{\text{ + }}{{{{\overline {\boldsymbol A}}}}_v}} \right) + \right. \\& \left.\sigma _n^2\left( {{\overline{\boldsymbol \rho }} + {{\boldsymbol{\rho }}_n}{\varDelta ^{\text{H}}} + \varDelta {{\boldsymbol{\rho }}_n}} \right){{\boldsymbol{A}}_v}{{\left( {{\boldsymbol{A}}_v^{\text{H}}{{\boldsymbol{A}}_v}} \right)}^{ - 1}}{\boldsymbol{R}}_S^{ - 1} \right]. \end{split} (24) 式(24)表明, 误差项
{\boldsymbol{\varDelta }},{\text{ }}{{{\overline {\boldsymbol A}}}_v},{\text{ }}{{\overline{\boldsymbol \rho }}_n} 影响了{{\boldsymbol{\widehat R}}_v} 噪声子空间{{\boldsymbol{\widehat U}}_{vN}} , 导致{{\boldsymbol{\widehat U}}_{vN}} 与导向矢量{{\boldsymbol{A}}_v} 的关系由{\boldsymbol{U}}_{vN}^{\text{H}}{{\boldsymbol{A}}_v} = 0 的相互正交, 变化为式(24)中{\overline{\boldsymbol U}}_{vN}^{\text{H}}{{\boldsymbol{A}}_v} 右侧不为零的扰动量。忽略系统误差影响, 估计误差中有限快拍数导致协方差矩阵偏离理想统计特性, 信噪比决定了实际噪声与理想假设的偏差对阵列协方差矩阵的影响程度。以有限快拍数为例分析
{{\boldsymbol{\widehat R}}_v} 的正规性与估计性能。对于Nehorai传统声矢量阵MUSIC方法, 利用有限次快拍
L 估计协方差矩阵{{\boldsymbol{\widehat R}}_v} , 有{{\boldsymbol{\widehat R}}_v} = \frac{1}{L}\sum\limits_{l = 1}^L {{\boldsymbol{y}}\left( n \right){{\boldsymbol{y}}^{\text{H}}}\left( n \right)} . (25) 显然
{{\boldsymbol{\widehat R}}_v}{\text{ = }}{\boldsymbol{\widehat R}}_v^{\text{H}} ,{{\boldsymbol{\widehat R}}_v} 仍为Hermite矩阵, 但在有限快拍数条件下, 信号和噪声没有足够的样本用以“解相关”, 噪声协方差并未收敛到理想值。因此, 由{{\boldsymbol{\widehat R}}_v} 较小的3M - K 个特征值对应的噪声子空间{{\boldsymbol{\widehat U}}_{vN}} 与理想噪声子空间{{\boldsymbol{U}}_{vN}} 之间存在偏差, 导致{{\boldsymbol{\widehat U}}_{vN}} 与{{\boldsymbol{A}}_v} 并不能完全正交, 式(8)并不成立。2.2 存在模型误差的声压振速联合处理协方差矩阵
2.2.1 系统误差的影响
考虑系统误差, 忽略有限快拍数等估计误差影响。假设协方差矩阵
{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 能够精确测量, 模型误差条件下声矢量阵声压通道输出{\boldsymbol{\widehat p}}\left( n \right) 和振速{v_x},{\text{ }}{v_y} 通道输出{{\boldsymbol{\widehat v}}_x}\left( n \right),{\text{ }}{{\boldsymbol{\widehat v}}_y}\left( n \right) 可表示为\begin{split}& {\boldsymbol{\widehat p}}\left( n \right) = {{\boldsymbol{\varGamma }}_{gp}}\left[ {{{\boldsymbol{\varGamma }}_{\phi p}}{\boldsymbol{As}}\left( n \right) + {{\boldsymbol{n}}_p}\left( n \right)} \right]{\text{ = }}{{{{\widehat {\boldsymbol A}}}}_p}{\boldsymbol{s}}\left( n \right) + {{{\boldsymbol{\widehat n}}}_p}\left( n \right), \\& {{{\boldsymbol{\widehat v}}}_x}\left( n \right) = {{\boldsymbol{\varGamma }}_{gx}}\left[ {{{\boldsymbol{\varGamma }}_{\phi x}}{\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{vx}}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_{vx}}\left( n \right)} \right]{\text{ = }}{{{{\widehat {\boldsymbol A}}}}_{vx}}{{\boldsymbol{\varPhi }}_{vx}}{\boldsymbol{s}}\left( n \right) + {{{\boldsymbol{\widehat n}}}_{vx}}\left( n \right), \\& {{{\boldsymbol{\widehat v}}}_y}\left( n \right) = {{\boldsymbol{\varGamma }}_{gy}}\left[ {{{\boldsymbol{\varGamma }}_{\phi y}}{\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{vy}}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_{vy}}\left( n \right)} \right] = {{{{\widehat {\boldsymbol A}}}}_{vy}}{{\boldsymbol{\varPhi }}_{vy}}{\boldsymbol{s}}\left( n \right) + {{{\boldsymbol{\widehat n}}}_{vy}}\left( n \right), \end{split} (26) 式中,
{{\boldsymbol{\varGamma }}_{gp}},{\text{ }}{{\boldsymbol{\varGamma }}_{gx}},{\text{ }}{{\boldsymbol{\varGamma }}_{gy}} 分别为声压通道、振速{v_x},{\text{ }}{v_y} 通道的同时影响信号与噪声分量的误差矩阵, 为简化分析, 以各通道增益误差为例, 其他误差分析方法与其类似;{{\boldsymbol{\varGamma }}_{\phi p}},{{\boldsymbol{\varGamma }}_{\phi x}},{{\boldsymbol{\varGamma }}_{\phi y}} 分别为仅影响声压通道、振速{v_x},{\text{ }}{v_y} 通道的阵列响应的误差矩阵, 以各通道相位误差为例, 其他误差分析方法与其类似。定义\begin{split}& {{\boldsymbol{\varGamma}} }_{gi}={{\boldsymbol{I}}}_{M} + {{\boldsymbol{\varDelta}} }_{gi}\text{, }{{\boldsymbol{\varDelta}} }_{gi}\text{=diag}\left[{g}_{i1},\cdots ,{g}_{iM}\right]\text{, }\\& {{\boldsymbol{\varGamma}} }_{\phi i}\text{=diag}\left[\mathrm{exp}\left(\text{j}{\phi }_{i1}\right),\cdots ,\mathrm{exp}\left(\text{j}{\phi }_{iM}\right)\right]\text{, }i\in p,x,y, \end{split} (27) 式中,
{g_{pm}},{\text{ }}{g_{xm}},{\text{ }}{g_{ym}} 分别表示各通道的增益扰动, 它们为统计独立、同分布的零均值高斯随机变量, 即{g_{pm}} \sim N\left( {0,\sigma _{gp}^2} \right) ;{\phi _{pm}},\,{\phi _{xm}},\,{\phi _{ym}} 分别表示各通道的相位扰动, 它们也是统计独立、同分布的零均值高斯随机变量, 即{\phi _{pm}} \sim N\left( {0,\sigma _{\phi p}^2} \right) 。阵列输出矢量
{\boldsymbol{\widehat y}}\left( n \right) 的增益误差对角矩阵{{\boldsymbol{\varGamma }}_g} 由{{\boldsymbol{\varGamma }}_{gp}},{{\boldsymbol{\varGamma }}_{gx}},{{\boldsymbol{\varGamma }}_{gy}} 对角元素构成, 相位误差对角矩阵{{\boldsymbol{\varGamma }}_\phi } 由{{\boldsymbol{\varGamma }}_{\phi p}},{{\boldsymbol{\varGamma }}_{\phi x}},{{\boldsymbol{\varGamma }}_{\phi y}} 对角元素构成, 则存在模型误差时,{\boldsymbol{\widehat y}}\left( n \right) 可表示为{\boldsymbol{\widehat y}}\left( n \right) = {{\boldsymbol{\varGamma }}_g}\left[ {{{\boldsymbol{\varGamma }}_\phi }{{\boldsymbol{A}}_v}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{n}}_v}\left( n \right)} \right] = {{{\widehat {\boldsymbol A}}}_v}{\boldsymbol{s}}\left( n \right) + {{\boldsymbol{\widehat n}}_v}\left( n \right), (28) 式中,
{{{\widehat {\boldsymbol A}}}_v}{\text{ = }}{{\boldsymbol{\varGamma }}_g}{{\boldsymbol{\varGamma }}_\phi }{{\boldsymbol{A}}_v} ,{{\boldsymbol{\widehat n}}_v}\left( n \right){\text{ = }}{{\boldsymbol{\varGamma }}_g}{{\boldsymbol{n}}_v}\left( n \right) 。存在模型误差的Nehorai传统声矢量阵协方差矩阵{{\boldsymbol{\widehat R}}_v} 可表示为{{\boldsymbol{\widehat R}}_v} = {\text{E}}\left[ {{\boldsymbol{\widehat y}}\left( n \right){{{\boldsymbol{\widehat y}}}^{\text{H}}}\left( n \right)} \right]{\text{ = }}{{\boldsymbol{\varGamma }}_g}\left[ {{{\boldsymbol{\varGamma }}_\phi }{{\boldsymbol{A}}_v}{{\boldsymbol{R}}_S}{\boldsymbol{A}}_v^{\text{H}}{\boldsymbol{\varGamma }}_\phi ^{\text{H}} + \sigma _n^2\left( {{{\boldsymbol{\rho }}_n} + {{{\overline{\boldsymbol \rho }}}_n}} \right)} \right]{\boldsymbol{\varGamma }}_g^{\text{H}}, (29) 满足式(20)的模型, 对应误差项
{\boldsymbol{\varDelta }},{\text{ }}{{{\overline {\boldsymbol A}}}_v} , 有{{\boldsymbol{\varGamma }}_g} = {{\boldsymbol{I}}_{3M}} + {\boldsymbol{\varDelta }} ,{{\boldsymbol{\varGamma }}_\phi }{{\boldsymbol{A}}_v} = {{\boldsymbol{A}}_v} + {{{\overline {\boldsymbol A}}}_v} 。则存在模型误差的声压振速联合处理协方差矩阵{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 可表示为{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = {\text{E}}\left\{ {\left[ {{\boldsymbol{\widehat p}}\left( n \right) + {{{\boldsymbol{\widehat v}}}_c}\left( n \right)} \right]{\boldsymbol{\widehat v}}_c^{\text{H}}\left( n \right)} \right\} = {{{\widehat {\boldsymbol A}}}_{cc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{vc}^{\text{H}} + {{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}, (30) 式中,
{{\boldsymbol{\widehat v}}_c}\left( n \right) 为存在模型误差条件下的组合振速, 有\begin{split}& {{{\boldsymbol{\widehat v}}}_c}\left( n \right){\text{ = }}{{{\boldsymbol{\widehat v}}}_x}\left( n \right)\cos \left( {{\theta _r}} \right) + {{{\boldsymbol{\widehat v}}}_y}\left( n \right)\sin \left( {{\theta _r}} \right) = {{{{\widehat {\boldsymbol A}}}}_{vc}}{\boldsymbol{s}}\left( n \right) + {{{\boldsymbol{\widehat n}}}_{vc}}\left( n \right), \\& {{{{\widehat {\boldsymbol A}}}}_{vc}}{\text{ = }}{{\boldsymbol{\varGamma }}_{gx}}{{\boldsymbol{\varGamma }}_{\phi x}}{\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{vx}}\cos \left( {{\theta _r}} \right){\text{ + }}{{\boldsymbol{\varGamma }}_{gy}}{{\boldsymbol{\varGamma }}_{\phi y}}{\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{vy}}\sin \left( {{\theta _r}} \right), \\& {{{\boldsymbol{\widehat n}}}_{vc}}\left( n \right) = {{\boldsymbol{\varGamma }}_{gx}}{{\boldsymbol{n}}_{vx}}\left( n \right)\cos \left( {{\theta _r}} \right) + {{\boldsymbol{\varGamma }}_{gy}}{{\boldsymbol{n}}_{vy}}\left( n \right)\sin \left( {{\theta _r}} \right), \end{split} (31) 式中
{{{\widehat {\boldsymbol A}}}_{cc}} = {{{\widehat {\boldsymbol A}}}_p} + {{{\widehat {\boldsymbol A}}}_{vc}} ,{{{\widehat {\boldsymbol A}}}_p}{\text{ = }}{{\boldsymbol{\varGamma }}_{gp}}{{\boldsymbol{\varGamma }}_{\phi p}}{\boldsymbol{A}} ,{{\boldsymbol{\widehat n}}_p}\left( n \right){\text{ = }}{{\boldsymbol{\varGamma }}_{gp}}{{\boldsymbol{n}}_p}\left( n \right) ,{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 为噪声协方差矩阵:\begin{split}& {{{\boldsymbol{\widehat R}}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = {\text{E}}\left\{ {\left[ {{{{\boldsymbol{\widehat n}}}_p}\left( n \right){\text{ + }}{{{\boldsymbol{\widehat n}}}_{vc}}\left( n \right)} \right]{\boldsymbol{\widehat n}}_{vc}^{\text{H}}\left( n \right)} \right\}= \\& {\text{E}}\left[ {{{\boldsymbol{\varGamma }}_{gx}}{{\boldsymbol{n}}_{vx}}\left( n \right){\boldsymbol{n}}_{vx}^{\text{H}}\left( n \right){\boldsymbol{\varGamma }}_{gx}^{\text{H}}} \right]{\cos ^2}\left( {{\theta _r}} \right)+\\& {\text{ E}}\left[ {{{\boldsymbol{\varGamma }}_{gy}}{{\boldsymbol{n}}_{vy}}\left( n \right){\boldsymbol{n}}_{vy}^{\text{H}}\left( n \right){\boldsymbol{\varGamma }}_{gy}^{\text{H}}} \right]{\sin ^2}\left( {{\theta _r}} \right) + \\& {\text{E}}\left[ {{{\boldsymbol{\varGamma }}_{gp}}{{\boldsymbol{n}}_p}\left( n \right){\boldsymbol{n}}_{vx}^{\text{H}}\left( n \right){\boldsymbol{\varGamma }}_{gx}^{\text{H}}} \right]\cos \left( {{\theta _r}} \right)+\\& {\text{ E}}\left[ {{{\boldsymbol{\varGamma }}_{gp}}{{\boldsymbol{n}}_p}\left( n \right){\boldsymbol{n}}_{vy}^{\text{H}}\left( n \right){\boldsymbol{\varGamma }}_{gy}^{\text{H}}} \right]\sin \left( {{\theta _r}} \right) + \\& \left\{ {\text{E}}\left[ {{{\boldsymbol{\varGamma }}_{gy}}{{\boldsymbol{n}}_{vy}}\left( n \right){\boldsymbol{n}}_{vx}^{\text{H}}\left( n \right){\boldsymbol{\varGamma }}_{gx}^{\text{H}}} \right] +\right. \\& \left.{\text{E}}\left[ {{{\boldsymbol{\varGamma }}_{gx}}{{\boldsymbol{n}}_{vx}}\left( n \right){\boldsymbol{n}}_{vy}^{\text{H}}\left( n \right){\boldsymbol{\varGamma }}_{gy}^{\text{H}}} \right] \right\}\sin \left( {{\theta _r}} \right)\cos \left( {{\theta _r}} \right). \end{split} (32) 令式(32)后4项等于
\sigma _{nv}^2{{\overline{\boldsymbol \rho }}_{nc}} , 其中{{\overline{\boldsymbol \rho }}_{nc}} 表示受增益误差影响的噪声偏差量, 忽略有限快拍数影响时{{\overline{\boldsymbol \rho }}_{nc}} 为Hermite矩阵, 并不影响协方差矩阵{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 是否正规, 则{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 可化简为{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = \sigma _{nv}^2{{\boldsymbol{I}}_M}\left[ {{{\boldsymbol{\varGamma }}_{gx}}{\boldsymbol{\varGamma }}_{gx}^{\text{H}}{{\cos }^2}\left( {{\theta _r}} \right) + {{\boldsymbol{\varGamma }}_{gy}}{\boldsymbol{\varGamma }}_{gy}^{\text{H}}{{\sin }^2}\left( {{\theta _r}} \right){\text{ + }}{{{\overline{\boldsymbol \rho }}}_{nc}}} \right]. (33) 可以证明,
{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 并非正规矩阵。由于声压和振速通道的阵列响应误差统计独立, 使{{{\widehat {\boldsymbol A}}}_{cc}} = \left( {{{{{\widehat {\boldsymbol A}}}}_p} + {{{{\widehat {\boldsymbol A}}}}_{vc}}} \right) \ne {{{\widehat {\boldsymbol A}}}_{vc}} , 即便在式(33)中有{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = {\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}} , 但是对{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} :{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}} = {{{\widehat {\boldsymbol A}}}_{vc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{cc}^{\text{H}} + {\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}}. (34) 式(30)与式(34)中信号项并不相等,
{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} \ne {\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}} 。进一步有\begin{split} & {{{\boldsymbol{\widehat R}}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}} = {{{{\widehat {\boldsymbol A}}}}_{cc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{vc}^{\text{H}}{{{{\widehat {\boldsymbol A}}}}_{vc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{cc}^{\text{H}}{\text{ + }}{{{\boldsymbol{\widehat R}}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}}, \\& {\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}}{{{\boldsymbol{\widehat R}}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = {{{{\widehat {\boldsymbol A}}}}_{vc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{cc}^{\text{H}}{{{{\widehat {\boldsymbol A}}}}_{cc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{vc}^{\text{H}} + {\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}}{{{\boldsymbol{\widehat R}}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}. \end{split} (35) 显然,
{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}} \ne {\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}}{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 。当
{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 不是正规矩阵时, 其各特征子空间之间的正交性不再满足。这使各信源对应的信号子空间之间以及信号子空间与噪声子空间额外增加了“相关性”, 这种“相关性”扩大了误差项{\boldsymbol{\varDelta }},{\text{ }}{{{\overline {\boldsymbol A}}}_v},{\text{ }}{{\overline{\boldsymbol \rho }}_n} 对噪声子空间估计值{{\boldsymbol{\widehat U}}_{cN}} 的影响。2.2.2 估计误差的影响
以有限快拍数为例, 考虑估计误差对噪声协方差矩阵的正规性的影响, 利用有限次快拍
L 估计协方差矩阵{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} , 有{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{\text{=}}\frac{1}{L}\sum\limits_{l = 1}^L {\left[ {{\boldsymbol{p}}\left( n \right){\text{ + }}{{\boldsymbol{v}}_c}\left( n \right)} \right]{\boldsymbol{v}}_c^{\text{H}}\left( n \right)} {\text{=}}{\boldsymbol{A}}{{\boldsymbol{\widehat R}}_{S\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{{\boldsymbol{A}}^{\text{H}}} + {{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}, (36) 式中,
{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 为有限快拍数的\left( {p + {v_c}} \right){v_c} 噪声协方差矩阵:{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} = \frac{1}{L}\sum\limits_{l = 1}^L {\left[ {{{\boldsymbol{n}}_p}\left( n \right){\boldsymbol{n}}_{vc}^{\text{H}}\left( n \right)} \right]} {\text{ + }}\frac{1}{L}\sum\limits_{l = 1}^L {\left[ {{{\boldsymbol{n}}_{vc}}\left( n \right){\boldsymbol{n}}_{vc}^{\text{H}}\left( n \right)} \right]} . (37) 定义
{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 的第1项为{{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}} , 当噪声的声压与振速分量的互协方差不可忽略时, 根据式(21)的定义,{{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}} 可写为\begin{split} {{{\boldsymbol{\widehat R}}}_{N{\boldsymbol{pv}}}}{\text{ = }}& \frac{1}{L}\sum\limits_{l = 1}^L {\left[ {{{\boldsymbol{n}}_p}\left( n \right){\boldsymbol{n}}_{vx}^{\text{H}}\left( n \right)\cos \left( {{\theta _r}} \right) + {{\boldsymbol{n}}_p}\left( n \right){\boldsymbol{n}}_{vy}^{\text{H}}\left( n \right)\sin \left( {{\theta _r}} \right)} \right]}= \\& \sigma _n^2\left[ {{{{\boldsymbol{\widehat \rho }}}_{px}}\cos \left( {{\theta _r}} \right){\text{ + }}{{{\boldsymbol{\widehat \rho }}}_{py}}\sin \left( {{\theta _r}} \right)} \right],\\[-1pt] \end{split} (38) 式中,
{{\boldsymbol{\widehat \rho }}_{px}},{\text{ }}{{\boldsymbol{\widehat \rho }}_{py}} 分别为有限快拍数条件下声压与振速{v_x},{\text{ }}{v_y} 通道的互相关系数矩阵。定义{\widehat \rho _{ij}} 为{{\boldsymbol{\widehat \rho }}_{px}} 第i 行第j 列元素, 表示有限快拍数条件下第i 个阵元声压与第j 个阵元振速的相关系数。当快拍数
L \to \infty 时,{{\boldsymbol{\widehat \rho }}_{px}}{\text{ = }}{{\boldsymbol{\rho }}_{px}} 。定义{\rho _{ij}} 为{{\boldsymbol{\rho }}_{px}} 第i 行第j 列元素, 则根据图3, 理论上空间间距相同的两阵元声压与振速的相关系数相同, 即第i 个阵元声压与第j 个阵元振速的相关系数{\rho _{ij}} 和第j 个阵元声压与第i 个阵元振速的相关系数{\rho _{ji}} 相等, 所以有{{\boldsymbol{\rho }}_{px}}{\text{ = }}{\boldsymbol{\rho }}_{px}^{\text{H}} 。类似地,{{\boldsymbol{\rho }}_{py}}{\text{ = }}{\boldsymbol{\rho }}_{py}^{\text{H}} , 所以有{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}^{\text{H}}{\text{ = }}\sigma _n^2\left[ {{\boldsymbol{\widehat \rho }}_{px}^{\text{H}}\cos \left( {{\theta _r}} \right){\text{ + }}{\boldsymbol{\widehat \rho }}_{py}^{\text{H}}\sin \left( {{\theta _r}} \right)} \right]{\text{ = }}{{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}}, (39) 即当快拍数
L \to \infty 时,{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 仍为Hermite矩阵。2.1节给出的噪声场偏差{{\overline{\boldsymbol \rho }}_n} 本身并不影响协方差矩阵{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 是否正规。但当快拍数有限时, 噪声协方差矩阵
{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 可能偏离理论统计特性,{{\boldsymbol{\widehat \rho }}_{px}},{\text{ }}{{\boldsymbol{\widehat \rho }}_{py}} 未能收敛至理论值, 相关系数估计值{\widehat \rho _{ij}},{\text{ }}{\widehat \rho _{ji}} 不再相等, 所以{{\boldsymbol{\widehat \rho }}_{px}} \ne {\boldsymbol{\widehat \rho }}_{px}^{\text{H}} 。尽管{\widehat \rho _{ij}},{\text{ }}{\widehat \rho _{ji}} 均为小量, 但也会导致{{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}} \ne {\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}^{\text{H}} , 即{{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}} = \frac{1}{L}\sum\limits_{l = 1}^L {\left[ {{{\boldsymbol{n}}_p}\left( n \right){\boldsymbol{n}}_{vc}^{\text{H}}\left( n \right)} \right]} \ne \frac{1}{L}\sum\limits_{l = 1}^L {\left[ {{{\boldsymbol{n}}_{vc}}\left( n \right){\boldsymbol{n}}_p^{\text{H}}\left( n \right)} \right]} {\text{ = }}{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}^{\text{H}}. (40) 根据上式, 可得
{{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}}{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}^{\text{H}} \ne {{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}}{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}^{\text{H}} ,{{\boldsymbol{\widehat R}}_{N{\boldsymbol{pv}}}} 非正规矩阵, 使{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 也不是正规矩阵。当
{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 不再为正规矩阵时, 噪声子空间估计值{{\boldsymbol{\widehat U}}_{cN}} 与噪声子空间理想值{{\boldsymbol{U}}_{cN}} 之间的偏差进一步扩大。该条件下,{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 各特征向量之间是线性相关的, 这增加了信号子空间和噪声子空间之间的“相关性”, 相当于有限快拍数扩大了噪声协方差{{\boldsymbol{\widehat R}}_{N\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 不精确的误差{{\overline{\boldsymbol \rho }}_n} 。2.3 基于奇异值分解的声压振速联合处理MUSIC改进方法
基于奇异值分解重建声压振速联合处理MUSIC空间谱。受模型误差影响,
{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 非正规矩阵, 其特征向量之间不再线性无关。但{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 的左、右奇异向量自身仍是线性无关的[21], 可以利用奇异向量张成{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 的噪声子空间。对
{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 进行奇异值分解并将其按奇异值大小降序排列:\begin{split} {{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{\text{ = }}&{{\boldsymbol{U}}_s}{{\boldsymbol{\varLambda }}_s}{\boldsymbol{V}}_s^{\text{H}}{\text{ = }}\sum\limits_{m = 1}^M {{\lambda _{sm}}{{\boldsymbol{u}}_{sm}}{\boldsymbol{v}}_{sm}^{\text{H}}} =\\ & {{\boldsymbol{U}}_{sS}}{{\boldsymbol{\varLambda }}_{sS}}{\boldsymbol{V}}_{sS}^{\text{H}} + {{\boldsymbol{U}}_{sN}}{{\boldsymbol{\varLambda }}_{sN}}{\boldsymbol{V}}_{sN}^{\text{H}}, \end{split} (41) 式中,
{{\boldsymbol{\varLambda }}_s} = {\text{diag}}\left( {{\lambda _{s1}}, \ldots ,{\lambda _{sM}}} \right) ,{\varLambda _m} 为{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 第m 个奇异值, 且{\lambda _{s1}} \geqslant \cdots \geqslant {\lambda _{sK}} > {\lambda _{sK + 1}} \geqslant \cdots \geqslant {\lambda _{sM}} ;{{\boldsymbol{U}}_s},{\text{ }}{{\boldsymbol{V}}_s} 分别为{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 的左、右奇异向量, 均为M \times M 维酉矩阵;{{\boldsymbol{u}}_{sm}} 为{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 的第m 列左奇异向量,{{\boldsymbol{v}}_{sm}} 为{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 的第m 列右奇异向量;{{\boldsymbol{U}}_{sS}}{\text{ = }}\left[ {{{\boldsymbol{u}}_{s1}}, \cdots ,{{\boldsymbol{u}}_{sK}}} \right] ,{{\boldsymbol{V}}_{sS}}{\text{ = }}\left[ {{{\boldsymbol{v}}_{s1}}, \cdots ,{{\boldsymbol{v}}_{sK}}} \right] 分别为较大K 个奇异值对应的左、右奇异向量;{{\boldsymbol{U}}_{sN}}{\text{ = }}\left[ {{{\boldsymbol{u}}_{sk + 1}}, \cdots ,{{\boldsymbol{u}}_{sM}}} \right] ,{{\boldsymbol{V}}_{sN}}{\text{ = }}\left[ {{{\boldsymbol{v}}_{sk + 1}}, \cdots ,{{\boldsymbol{v}}_{sM}}} \right] 分别为较小M - K 个奇异值对应的左、右奇异向量。已知
{{\boldsymbol{U}}_s},{\text{ }}{{\boldsymbol{V}}_s} 均为酉矩阵, 有{\boldsymbol{U}}_s^{\text{H}}{{\boldsymbol{U}}_s} = {\boldsymbol{V}}_s^{\text{H}}{{\boldsymbol{V}}_s} = {{\boldsymbol{I}}_M} , 则根据式(12)和式(41)可知:\begin{split} & {{\boldsymbol{R}}}_{\left({\boldsymbol{p + v}}\right)v}{{\boldsymbol{R}}}_{\left({\boldsymbol{p + v}}\right){\boldsymbol{v}}}^{\text{H}}= {\boldsymbol{A}}{{\boldsymbol{\varPhi}} }_{\left({\boldsymbol{p + v}}\right){\boldsymbol{v}}}{{\boldsymbol{R}}}_{S}{{\boldsymbol{A}}}^{\text{H}}{\boldsymbol{A}}{{\boldsymbol{R}}}_{S}{{\boldsymbol{\varPhi}} }_{\left({\boldsymbol{p + v}}\right){\boldsymbol{v}}}{{\boldsymbol{A}}}^{\text{H}} +\\ &\qquad {\left({\sigma }_{nv}^{2}\right)}^{2}{{\boldsymbol{I}}}_{M}={{\boldsymbol{U}}}_{s}{{\boldsymbol{\varLambda}} }_{s}^{2}{{\boldsymbol{U}}}_{s}^{\text{H}}\text{, }\\ & {{\boldsymbol{R}}}_{\left({\boldsymbol{p + v}}\right){\boldsymbol{v}}}^{\text{H}}{{\boldsymbol{R}}}_{\left({\boldsymbol{p + v}}\right){\boldsymbol{v}}}={\boldsymbol{A}}{{\boldsymbol{R}}}_{S}{{\boldsymbol{\varPhi}} }_{\left({\boldsymbol{p + v}}\right){\boldsymbol{v}}}{{\boldsymbol{A}}}^{\text{H}}{\boldsymbol{A}}{{\boldsymbol{\varPhi}} }_{\left({\boldsymbol{p + v}}\right){\boldsymbol{v}}}{{\boldsymbol{R}}}_{S}{{\boldsymbol{A}}}^{\text{H}} +\\ &\qquad {\left({\sigma }_{nv}^{2}\right)}^{2}{{\boldsymbol{I}}}_{M}={{\boldsymbol{V}}}_{s}{{\boldsymbol{\varLambda}} }_{s}^{2}{{\boldsymbol{V}}}_{s}^{\text{H}}. \end{split} (42) 显然, 矩阵
{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}} 和{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}}{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 始终为Hermite矩阵, 式(42)表明两矩阵的特征向量分别为{{\boldsymbol{U}}_s},{\text{ }}{{\boldsymbol{V}}_s} , 且不同奇异值对应的{{\boldsymbol{U}}_s},{\text{ }}{{\boldsymbol{V}}_s} 不同列向量之间各自相互正交。式(42)中两矩阵分别右乘{{\boldsymbol{U}}_{sN}},{\text{ }}{{\boldsymbol{V}}_{sN}} 后转置, 由于{{\boldsymbol{\varPhi }}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{{\boldsymbol{R}}_S}{{\boldsymbol{A}}^{\text{H}}}{\boldsymbol{A}}{{\boldsymbol{R}}_S}{{\boldsymbol{\varPhi }}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 满秩, 可得\begin{array}{cc}{{\boldsymbol{U}}}_{sN}^{\text{H}}{{\boldsymbol{a}}}\left({\theta }_{i}\right)=0\text{, }\;\;{{\boldsymbol{V}}}_{sN}^{\text{H}}{{\boldsymbol{a}}}\left({\theta }_{i}\right)=0,& i=1,\cdots ,K.\end{array} (43) 式(43)表明,
{{\boldsymbol{U}}_{sN}},{{\boldsymbol{V}}_{sN}} 均与导向矢量{\boldsymbol{A}} 正交, 此正交性与{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 本身的正规性无关。当
{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 为Hermite矩阵时, 有{{\boldsymbol{U}}_{sN}}{\text{ = }}{{\boldsymbol{V}}_{sN}} = {{\boldsymbol{U}}_{cN}} , 而模型误差下则并非如此。分析2.2节中模型误差对噪声子空间{{\boldsymbol{U}}_{sN}},{\text{ }}{{\boldsymbol{V}}_{sN}} 的扰动{{\boldsymbol{\widehat U}}_{sN}},{\text{ }}{{\boldsymbol{\widehat V}}_{sN}} 。定义各通道相位误差引起的阵列响应偏移量{{{\overline {\boldsymbol A}}}_p},{\text{ }}{{{\overline {\boldsymbol A}}}_{vx}},{\text{ }}{{{\overline {\boldsymbol A}}}_{vy}} , 有{{{\overline {\boldsymbol A}}}_p}{\text{ = }}\left( {{{\boldsymbol{\varGamma }}_{\phi p}} - {{\boldsymbol{I}}_M}} \right){\boldsymbol{A}} ,{{{\overline {\boldsymbol A}}}_{vx}} = \left( {{{\boldsymbol{\varGamma }}_{\phi x}} - {{\boldsymbol{I}}_M}} \right){\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{vx}} ,{{{\overline {\boldsymbol A}}}_{vy}} = ( {{\boldsymbol{\varGamma }}_{\phi y}} - {{\boldsymbol{I}}_M} ) {\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{vy}} , 将{{{\overline {\boldsymbol A}}}_p},{\text{ }}{{{\overline {\boldsymbol A}}}_{vx}},{\text{ }}{{{\overline {\boldsymbol A}}}_{vy}} 和式(27)代入式(30), 忽略二阶误差项, 可将{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 化简为\begin{split} & {\widehat{{\boldsymbol{R}}}}_{\left(p + v\right)v}={\widehat{{\boldsymbol{A}}}}_{cc}{{\boldsymbol{R}}}_{S}{\widehat{{\boldsymbol{A}}}}_{vc}^{\text{H}} + {\sigma }_{nv}^{2}\left({{\boldsymbol{I}}}_{M} + {{\boldsymbol{\varepsilon}} }_{\sigma }\right),\\ & {\widehat{{\boldsymbol{A}}}}_{vc}={\boldsymbol{A}}{{\boldsymbol{\varPhi}} }_{vc}\text{ + }{\boldsymbol{\varepsilon}} \left({{\boldsymbol{A}}}_{vc}\right)\text{, }~~{\widehat{{\boldsymbol{A}}}}_{cc}={\boldsymbol{A}}\left({{\boldsymbol{I}}}_{M}\text{ + }{{\boldsymbol{\varPhi}} }_{vc}\right)\text{ + }{\boldsymbol{\varepsilon}} \left({{\boldsymbol{A}}}_{p}\right)\text{ + }{\boldsymbol{\varepsilon}} \left({{\boldsymbol{A}}}_{vc}\right),\\ & {{\boldsymbol{\varepsilon}} }_{\sigma }=\left({{\boldsymbol{\varDelta}} }_{gx} + {{\boldsymbol{\varDelta}} }_{gx}^{\text{H}}\right){\mathrm{cos}}^{2}\left({\theta }_{r}\right)\text{ + }\left({{\boldsymbol{\varDelta}} }_{gy} + {{\boldsymbol{\varDelta}} }_{gy}^{\text{H}}\right){\mathrm{sin}}^{2}\left({\theta }_{r}\right)\text{ + }{\overline{{\boldsymbol{\rho}} }}_{nc}\text{, } \end{split} (44) 式中,
{\boldsymbol{\varepsilon }}\left( {{{\boldsymbol{A}}_p}} \right),{\text{ }}{\boldsymbol{\varepsilon }}\left( {{{\boldsymbol{A}}_{vc}}} \right) 分别表示{{{\widehat {\boldsymbol A}}}_p},{\text{ }}{{{\widehat {\boldsymbol A}}}_{vc}} 与真实值{{\boldsymbol{A}}_p},{\text{ }}{{\boldsymbol{A}}_{vc}} 的偏移量, 有\begin{split}& {\boldsymbol{\varepsilon }}\left( {{{\boldsymbol{A}}_{vc}}} \right) = {\boldsymbol{\varepsilon }}\left( {{{\boldsymbol{A}}_{vx}}} \right)\cos \left( {{\theta _r}} \right) + {\boldsymbol{\varepsilon }}\left( {{{\boldsymbol{A}}_{vy}}} \right)\sin \left( {{\theta _r}} \right){\boldsymbol{\varepsilon }}\left( {{{\boldsymbol{A}}_p}} \right) = {{{{\overline {\boldsymbol{A}}}}}_p} + {{\boldsymbol{\Delta }}_{gp}}{\boldsymbol{A}},\\& {\boldsymbol{\varepsilon }}\left( {{{\boldsymbol{A}}_{vx}}} \right) = {{{{\overline {\boldsymbol{A}}}}}_{vx}} + {{\boldsymbol{\varDelta }}_{gx}}{\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{vx}},~~{\boldsymbol{\varepsilon }}\left( {{{\boldsymbol{A}}_{vy}}} \right) = {{{{\overline {\boldsymbol{A}}}}}_{vy}} + {{\boldsymbol{\Delta }}_{gy}}{\boldsymbol{A}}{{\boldsymbol{\varPhi }}_{vy}}. \end{split} (45) 假定基于左、右奇异向量的扰动的噪声子空间分别为
{{\boldsymbol{\widehat U}}_{sN}}{\text{ = }}{{\boldsymbol{U}}_{sN}}{\text{ + }}{{{\overline {\boldsymbol{U}}}}_{sN}} ,{{\boldsymbol{\widehat V}}_{sN}}{\text{ = }}{{\boldsymbol{V}}_{sN}}{\text{ + }}{{{\overline {\boldsymbol{V}}}}_{sN}} , 根据式(42), 可通过下式定义{{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 与噪声子空间{{\boldsymbol{\widehat U}}_{sN}},{\text{ }}{{\boldsymbol{\widehat V}}_{sN}} 的关系:\begin{split}& {{{\boldsymbol{\widehat R}}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}}{{{\boldsymbol{\widehat U}}}_{sN}}{\text{ = }}{{{\boldsymbol{\widehat U}}}_{sN}}\left( {\sigma _{nv}^2{{\boldsymbol{I}}_M} + {{{{\overline {\boldsymbol \varLambda} }}}_s}} \right){\left( {\sigma _{nv}^2{{\boldsymbol{I}}_M} + {{{\overline{\boldsymbol {\boldsymbol{\varLambda}} }}}_s}} \right)^{\text{H}}}, \\& {\boldsymbol{\widehat R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}}{{{\boldsymbol{\widehat R}}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{{{\boldsymbol{\widehat V}}}_{sN}}{\text{ = }}{{{\boldsymbol{\widehat V}}}_{sN}}{\left( {\sigma _{nv}^2{{\boldsymbol{I}}_M} + {{{{\overline {\boldsymbol \varLambda} }}}_s}} \right)^{\text{H}}}\left( {\sigma _{nv}^2{{\boldsymbol{I}}_M} + {{{\overline{\boldsymbol {\boldsymbol{\varLambda}} }}}_s}} \right), \end{split} (46) 式中,
{{{\overline {\boldsymbol \varLambda} }}_{\boldsymbol{s}}} 表示扰动的噪声奇异值。由{\boldsymbol{U}}_{sN}^{\text{H}}{\boldsymbol{A}} = 0,{\text{ }}{\boldsymbol{V}}_{sN}^{\text{H}}{\boldsymbol{A}} = 0 , 忽略二阶误差项, 可得{{\boldsymbol{U}}_{sN}}\left( {{{{{\overline {\boldsymbol \varLambda} }}}_s} + {{\overline {\boldsymbol \varLambda} }}_s^{\text{H}}} \right) \doteq \sigma _{nv}^4\left( {{{\boldsymbol{\varepsilon }}_\sigma } + {\boldsymbol{\varepsilon }}_\sigma ^{\text{H}}} \right){{\boldsymbol{U}}_{sN}} + {{{{\widehat {\boldsymbol A}}}}_{cc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{vc}^{\text{H}}{{{{\widehat {\boldsymbol A}}}}_{vc}}{{\boldsymbol{R}}_S}\left\{ {\left[ {{{\boldsymbol{\varepsilon }}^{\text{H}}}\left( {{{\boldsymbol{A}}_p}} \right){\text{ + }}{{\boldsymbol{\varepsilon }}^{\text{H}}}\left( {{{\boldsymbol{A}}_{vc}}} \right)} \right]{{\boldsymbol{U}}_{sN}} + {{\left( {{{\boldsymbol{I}}_M}{\text{ + }}{{\boldsymbol{\varPhi }}_{vc}}} \right)}^{\text{H}}}{{\boldsymbol{A}}^{\text{H}}}{{{\overline{\boldsymbol U}}}_{sN}}} \right\}, (47) {{\boldsymbol{V}}_{sN}}\left( {{{{{\overline {\boldsymbol \varLambda} }}}_s} + {{\overline {\boldsymbol \varLambda} }}_s^{\text{H}}} \right) \doteq \sigma _{nv}^4\left( {{{\boldsymbol{\varepsilon }}_\sigma } + {\boldsymbol{\varepsilon }}_\sigma ^{\text{H}}} \right){{\boldsymbol{V}}_{sN}}{\text{ + }}{{{\widehat {\boldsymbol A}}}_{vc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{cc}^{\text{H}}{{{\widehat {\boldsymbol A}}}_{cc}}{{\boldsymbol{R}}_S}\left[ {{{\boldsymbol{\varepsilon }}^{\text{H}}}\left( {{{\boldsymbol{A}}_{vc}}} \right){{\boldsymbol{V}}_{sN}}{\text{ + }}{{\boldsymbol{\varPhi }}_{vc}}{{\boldsymbol{A}}^{\text{H}}}{{{\overline{\boldsymbol V}}}_{sN}}} \right]. (48) 式(47)和式(48)等式两侧同时左乘
{{\boldsymbol{A}}^{\text{H}}} , 继续化简并做共轭转置, 得{\overline{\boldsymbol U}}_{sN}^{\text{H}}{\boldsymbol{A}} \doteq - {\boldsymbol{U}}_{sN}^{\text{H}}\left\{ {\left[ {{\boldsymbol{\varepsilon }}\left( {{{\boldsymbol{A}}_p}} \right){\text{ + }}{\boldsymbol{\varepsilon }}\left( {{{\boldsymbol{A}}_{vc}}} \right)} \right] + \sigma _{nv}^4\left( {{{\boldsymbol{\varepsilon }}_\sigma } + {\boldsymbol{\varepsilon }}_\sigma ^{\text{H}}} \right){\boldsymbol{A}}{{\left( {{{\widehat {\boldsymbol A}}}_{vc}^{\text{H}}{{{{\widehat {\boldsymbol A}}}}_{vc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{cc}^{\text{H}}{\boldsymbol{A}}} \right)}^{ - 1}}{\boldsymbol{R}}_S^{ - 1}} \right\}{\left( {{{\boldsymbol{I}}_M}{\text{ + }}{{\boldsymbol{\varPhi }}_{vc}}} \right)^{ - 1}}, (49) {\overline{\boldsymbol V}}_{sN}^{\text{H}}{\boldsymbol{A}} \doteq - {\boldsymbol{V}}_{sN}^{\text{H}}\left[ {{\boldsymbol{\varepsilon }}\left( {{{\boldsymbol{A}}_{vc}}} \right) + \sigma _{nv}^4\left( {{{\boldsymbol{\varepsilon }}_\sigma } + {\boldsymbol{\varepsilon }}_\sigma ^{\text{H}}} \right){\boldsymbol{A}}{{\left( {{{\widehat {\boldsymbol A}}}_{cc}^{\text{H}}{{{{\widehat {\boldsymbol A}}}}_{cc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{vc}^{\text{H}}{\boldsymbol{A}}} \right)}^{ - 1}}{\boldsymbol{R}}_S^{ - 1}} \right]{\boldsymbol{\varPhi }}_{vc}^{ - 1}. (50) 对比式(24)中
{{\boldsymbol{\widehat R}}_v} 噪声子空间{{\boldsymbol{\widehat U}}_{vN}} 的扰动项{\overline{\boldsymbol U}}_{vN}^{\text{H}}{{\boldsymbol{A}}_v} , 式(49)和式(50)中{\overline{\boldsymbol U}}_{sN}^{\text{H}}{\boldsymbol{A}} ,{\overline{\boldsymbol V}}_{sN}^{\text{H}}{\boldsymbol{A}} 噪声扰动项正比于振速通道噪声功率\sigma _{nv}^2 的平方, 且乘以{{\widehat {\boldsymbol A}}}_{vc}^{\text{H}}{{{\widehat {\boldsymbol A}}}_{vc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{cc}^{\text{H}}{\boldsymbol{A}} 和{{\widehat {\boldsymbol A}}}_{cc}^{\text{H}}{{{\widehat {\boldsymbol A}}}_{cc}}{{\boldsymbol{R}}_S}{{\widehat {\boldsymbol A}}}_{vc}^{\text{H}}{\boldsymbol{A}} 的逆运算再归算为\sigma _{nv}^2 量级, 类似于“加权平方根”处理。根据式(43)中
{{\boldsymbol{U}}_{sN}},{\text{ }}{{\boldsymbol{V}}_{sN}} 与{\boldsymbol{A}} 的正交关系, 联合左右奇异向量构造基于奇异值分解的声压振速联合处理MUSIC空间谱:{P_{{\text{MUSIC - S}}}}\left( \theta \right) = {1 \mathord{\left/ {\vphantom {1 {\left[ {{{\boldsymbol{a}}^{\text{H}}}\left( \theta \right){{\boldsymbol{U}}_{sN}}{\boldsymbol{V}}_{sN}^{\text{H}}{\boldsymbol{a}}\left( \theta \right)} \right]}}} \right. } {\left[ {{{\boldsymbol{a}}^{\text{H}}}\left( \theta \right){{\boldsymbol{U}}_{sN}}{\boldsymbol{V}}_{sN}^{\text{H}}{\boldsymbol{a}}\left( \theta \right)} \right]}}. (51) 仅利用单侧奇异向量张成噪声子空间也是可行的, 这相当于利用矩阵
{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}}{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}} 或{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}^{\text{H}}{{\boldsymbol{R}}_{\left( {{\boldsymbol{p}} + {\boldsymbol{v}}} \right){\boldsymbol{v}}}} 的特征向量。本文以右奇异向量{{\boldsymbol{V}}_{sN}} 为例, 构造基于右奇异向量的声压振速联合处理MUSIC空间谱:{P_{{\text{MUSIC - R}}}}\left( \theta \right) = {1 \mathord{\left/ {\vphantom {1 {\left[ {{{\boldsymbol{a}}^{\text{H}}}\left( \theta \right){{\boldsymbol{V}}_{sN}}{\boldsymbol{V}}_{sN}^{\text{H}}{\boldsymbol{a}}\left( \theta \right)} \right]}}} \right. } {\left[ {{{\boldsymbol{a}}^{\text{H}}}\left( \theta \right){{\boldsymbol{V}}_{sN}}{\boldsymbol{V}}_{sN}^{\text{H}}{\boldsymbol{a}}\left( \theta \right)} \right]}}. (52) 3. 数值仿真与分析
数值仿真参数设置和定义如下: 声矢量均匀圆阵阵元数为8, 圆阵半径为
{\lambda\mathord{\left/ {\vphantom {\lambda2}} \right. } 2} ,\lambda 为波长, 两信源入射角度范围为\left[ {0,2\pi } \right] , 各窄带信源互不相关且功率相等, 背景噪声为带限的高斯白噪声, 滤波器通带频率为[800, 1200] Hz, 信噪比定义为处理带宽内时域信噪比,{\text{SNR = }}10{\log _{10}}\left( {{{\sigma _k^2} \mathord{\left/ {\vphantom {{\sigma _k^2} {\sigma _n^2}}} \right. } {\sigma _n^2}}} \right) ,\sigma _k^2 为单信源功率,\sigma _n^2 为声压通道噪声功率。均方根误差(RMSE)定义为
{\text{RMSE}} = \sqrt {\frac{1}{{NK}}\sum\limits_{n = 1}^N {\sum\limits_{k = 1}^K {{{\left( {{{\widehat \theta }_{n,k}} - {\theta _k}} \right)}^2}} } } , (53) 式中,
N 为蒙特卡罗实验次数,{\widehat \theta _{n,k}} 为第k 个信源第n 次蒙特卡罗实验的方位估计值。定义两目标成功分辨条件为\left| {{{\widehat \theta }_1} - {\theta _1}} \right| + \left| {{{\widehat \theta }_2} - {\theta _2}} \right| < \left| {{\theta _1} - {\theta _2}} \right|, (54) 式中,
{\theta _1},{\text{ }}{\theta _2} 为两信源方位真实值,{\widehat \theta _1},{\text{ }}{\widehat \theta _2} 为两信源方位估计值, 定义两目标成功分辨概率(SP)为两目标成功分辨次数占总蒙特卡罗实验次数的百分比。仿真设置观测角{\theta _r} 均为130°, 蒙特卡罗实验次数为500次。分别使用VMUSIC、CMUSIC、RMUSIC和SMUSIC表示Nehorai传统声矢量阵MUSIC方法、传统声压振速联合处理MUSIC方法和基于奇异值分解的两种声压振速联合处理MUSIC方法。3.1 有限快拍数影响分析
3.1.1 空间谱
假设信噪比为0 dB, 两信源方位角分别为120°, 150°。图4(a)(b)(c)分别为快拍数200, 2000, 200000时4种MUSIC方法的空间谱。由图4可知, 随着快拍数的增加, 4种方法的空间谱均有所改善; CMUSIC、RMUSIC和SMUSIC相较VMUSIC方法空间谱峰更为尖锐, 背景级更低, 这是因为基于声压振速联合处理的MUSIC方法利用声压振速组合指向性抑制噪声; 整体上, RMUSIC方法与CMUSIC方法背景级相仿, 但背景谱起伏更平坦, 且较小快拍数(200)时谱峰更尖锐, SMUSIC方法的空间谱估计性能优于RMUSIC、CMUSIC方法。这是由于较小快拍数时CMUSIC方法的噪声协方差偏离统计特性, 不再是Hermite矩阵, 噪声子空间的各特征向量线性相关, 与导向矢量的正交性更为随机, 使空间谱起伏较为剧烈; 较大快拍数(200000)时, CMUSIC方法的采样数据协方差矩阵接近Hermite矩阵, Hermite矩阵特征向量与奇异向量等价, 故随着快拍数增加, CMUSIC方法空间谱逐渐与RMUSIC、SMUSIC方法空间谱估计性能接近。
3.1.2 目标分辨能力
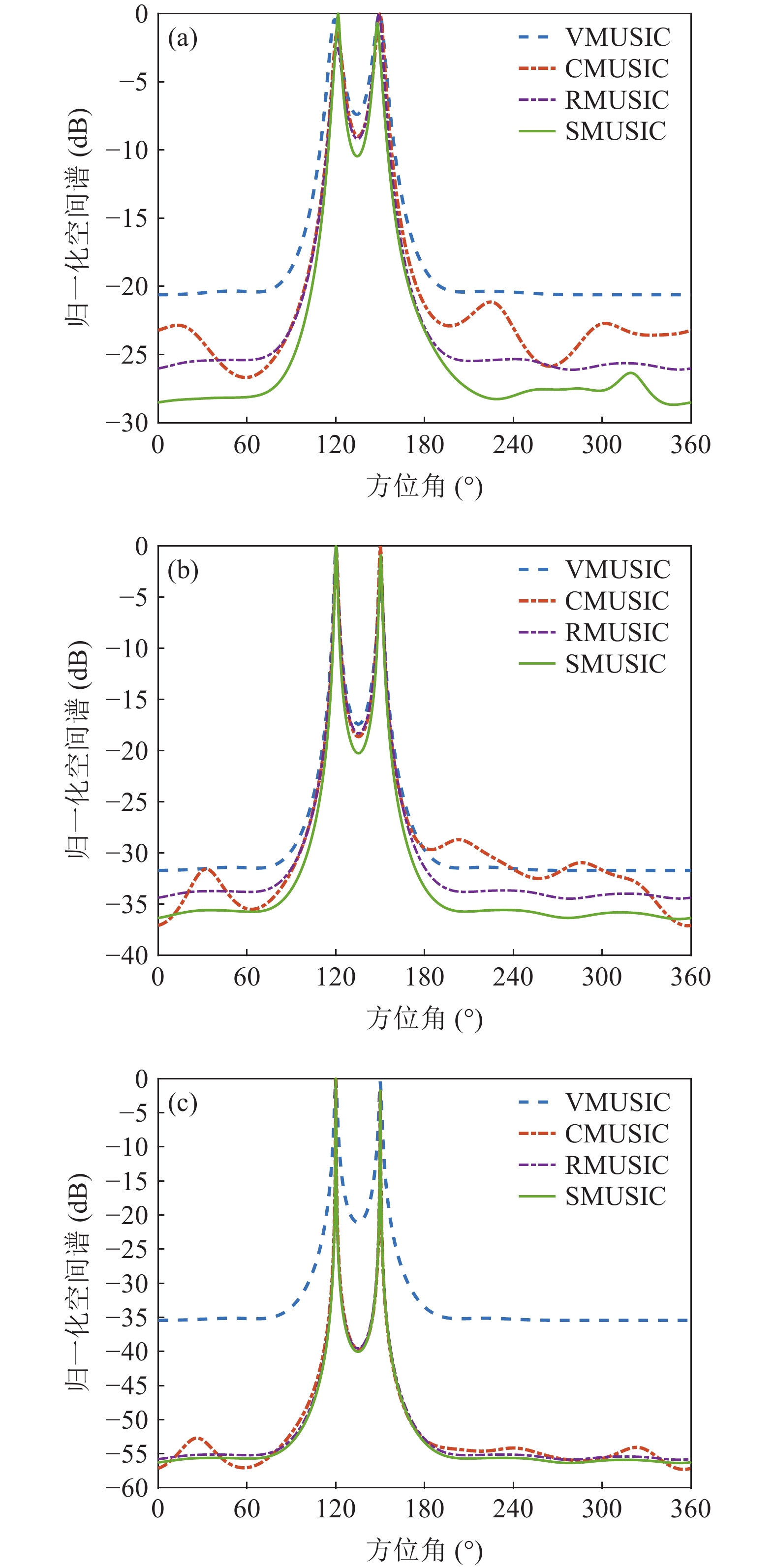
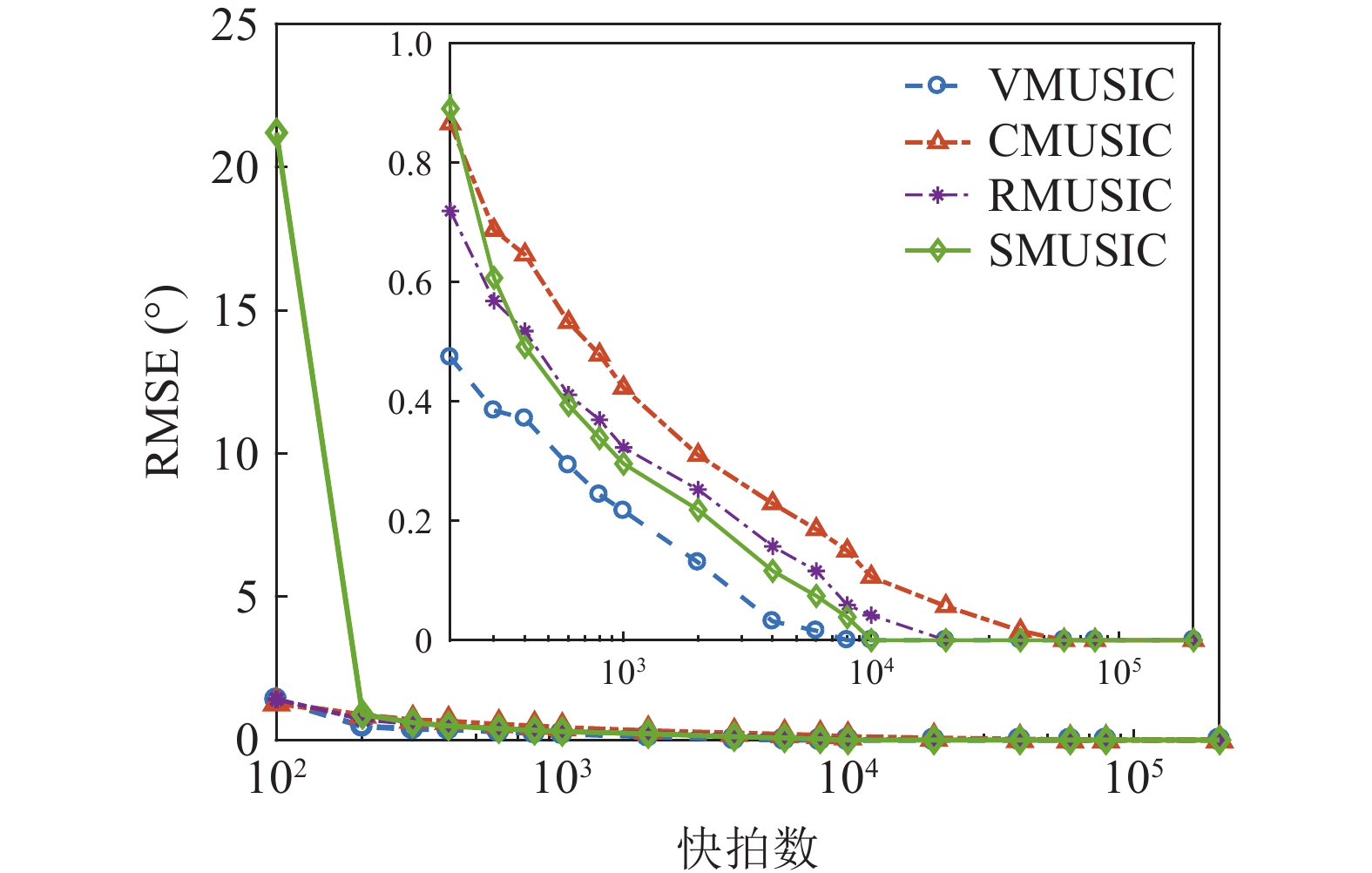
假设两信源方位角分别为120°和135°, 以验证4种MUSIC方法分辨两方位相近信源的能力。假设信噪比0 dB, 快拍数100~200000, 扫描角度间隔0.5°。图5(a)(b)分别为4种方法DOA估计结果的目标分辨概率和均方根误差随快拍数的变化情况。由图5可知, 整体上随着快拍数的增加, 4种方法的目标分辨能力均有所改善; 其中, SMUSIC、RMUSIC方法的目标分辨概率和均方根误差均较其他两种方法更具优势, 而SMUSIC性能又略优于RMUSIC方法; 随着快拍数增加, SMUSIC、RMUSIC和CMUSIC方法的均方根误差趋向0°, VMUSIC方法的均方根误差稳定在0.5°左右。这是由于受给定信噪比条件下VMUSIC的主瓣宽度限制, 两信源谱峰存在重叠, 估计出的两信源方位间距较实际更小, 即始终存在一定的均方根误差, 而如CMUSIC、RMUSIC和SMUSIC这类声压振速联合处理方法, 主瓣宽度更窄、目标分辨力更强, 故对两临近信源方位角的估计更为准确。
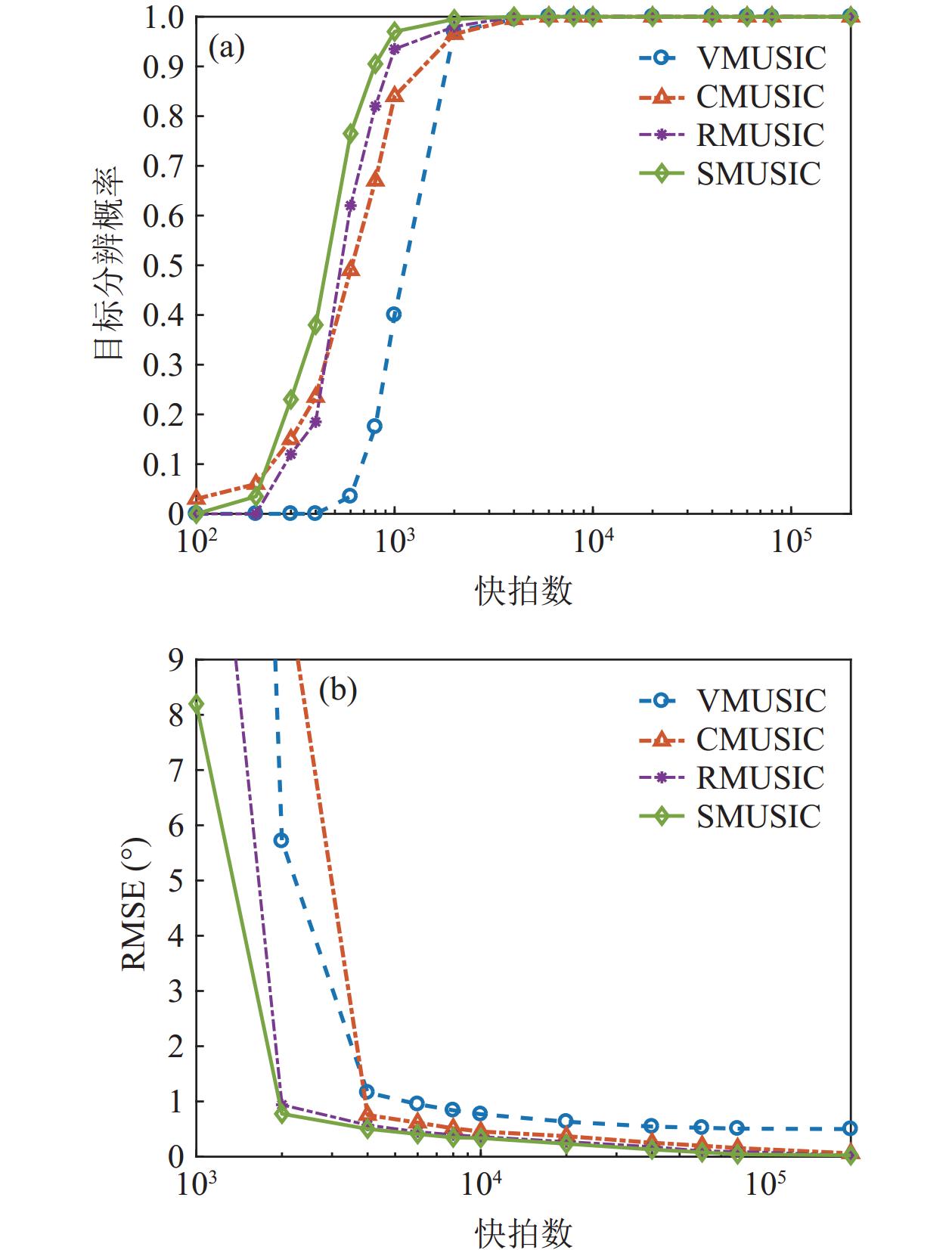
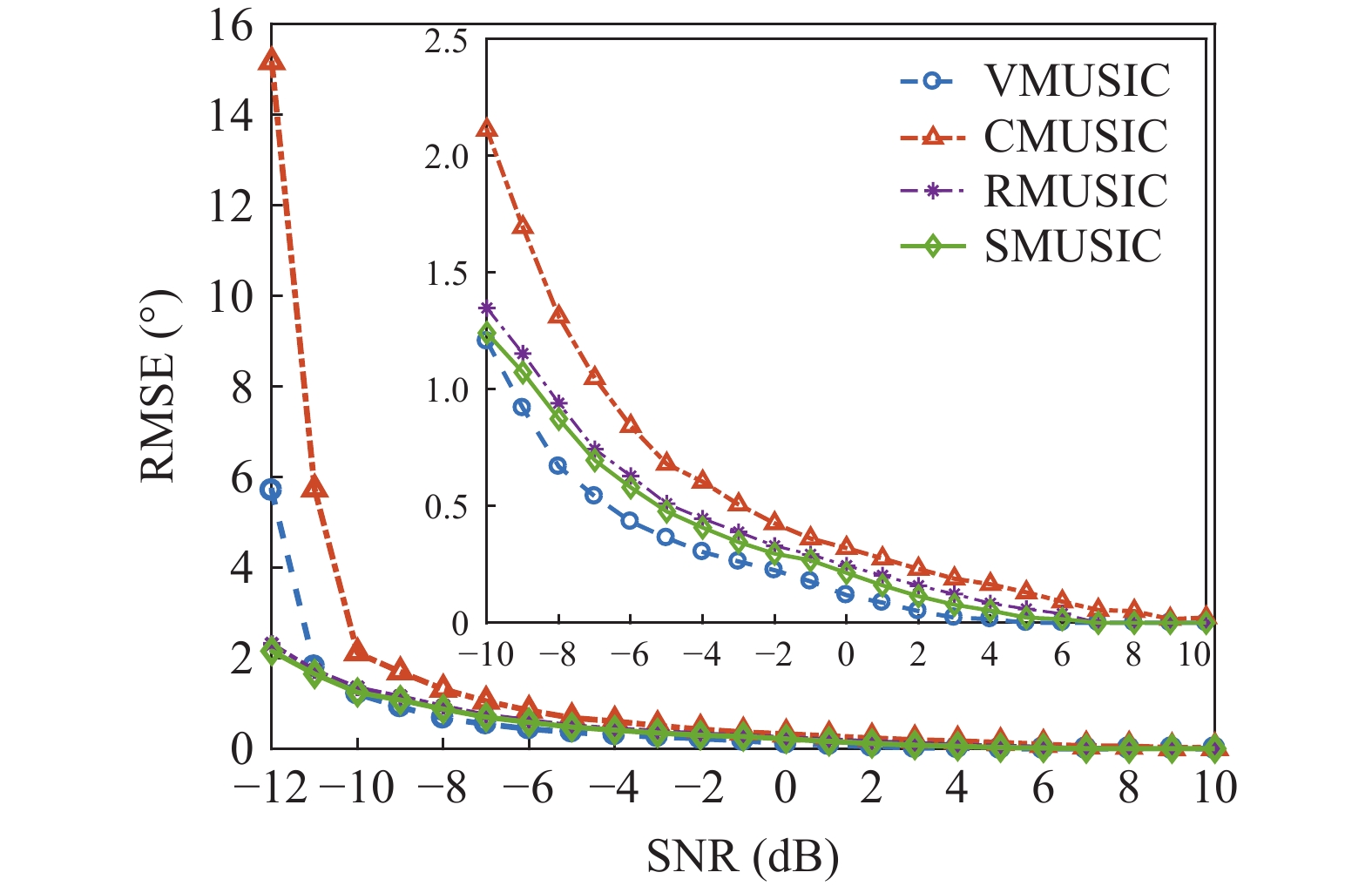
假设快拍数2000, 信噪比−12~10 dB, 扫描角度间隔0.5°。图6(a)(b)分别为4种MUSIC方法DOA估计结果的目标分辨概率和均方根误差随信噪比的变化情况。SMUSIC和RMUSIC方法的目标分辨能力优于CMUSIC和VMUSIC方法; SMUSIC方法的方位估计精度稍优于RMUSIC方法, 而两者的均方根误差始终较CMUSIC方法更小。当信噪比小于−2 dB时, 各方法难以分辨两相近信源, 导致均方根误差很大。随着信噪比增大, VMUSIC方法的均方根误差迅速减小, 信噪比大于4 dB时其方位估计精度为4种方法中最优。这是由于高信噪比条件下, 4种方法的主瓣宽度更窄, VMUSIC方法的两信源空间谱峰不再重叠, 其方位估计精度优势得以充分体现。
3.1.3 方位估计精度
假设两信源方位角分别为120°和160°, 以验证4种MUSIC方法的方位估计精度。假设信噪比0 dB, 快拍数100~200000, 扫描角度间隔0.5°, 图7为4种方法DOA估计结果的均方根误差随快拍数的变化情况。假设快拍数2000, 信噪比−12~10 dB, 扫描角度间隔0.5°, 图8为4种方法DOA估计结果的均方根误差随信噪比的变化情况。4种方法对大角度间隔的两信源方位的估计精度规律相同, 即CMUSIC方法的方位估计精度最差, SMUSIC方法优于RMUSIC方法, 但均逊于VMUSIC方法。这是由于SMUSIC、RMUSIC和CMUSIC方法从原理上均可归类为波束域MUSIC方法, 与直接在阵元域处理的VMUSIC相比, 方位估计精度稍差。图7中SMUSIC方法的均方根误差在快拍数小于200时迅速恶化, 表明其对小快拍的稳健性不如其他方法。图8中VMUSIC方法在信噪比小于−10 dB时的均方根误差高于RMUSIC和SMUSIC方法, 表明改进的MUSIC方法在低信噪比时的方位估计精度更具优势。
3.2 阵列幅相误差影响分析
3.2.1 空间谱
假设声矢量阵声压和振速
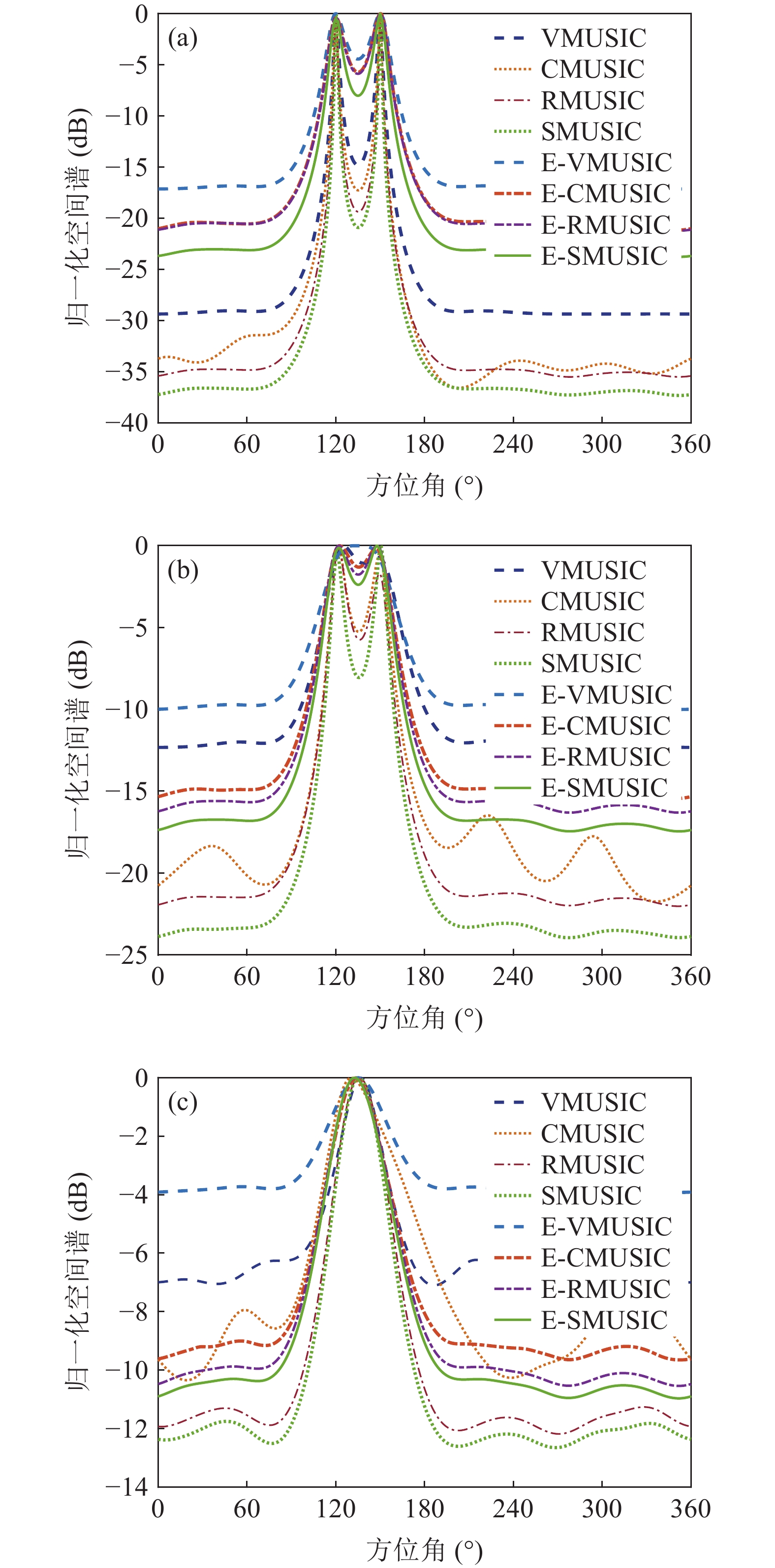
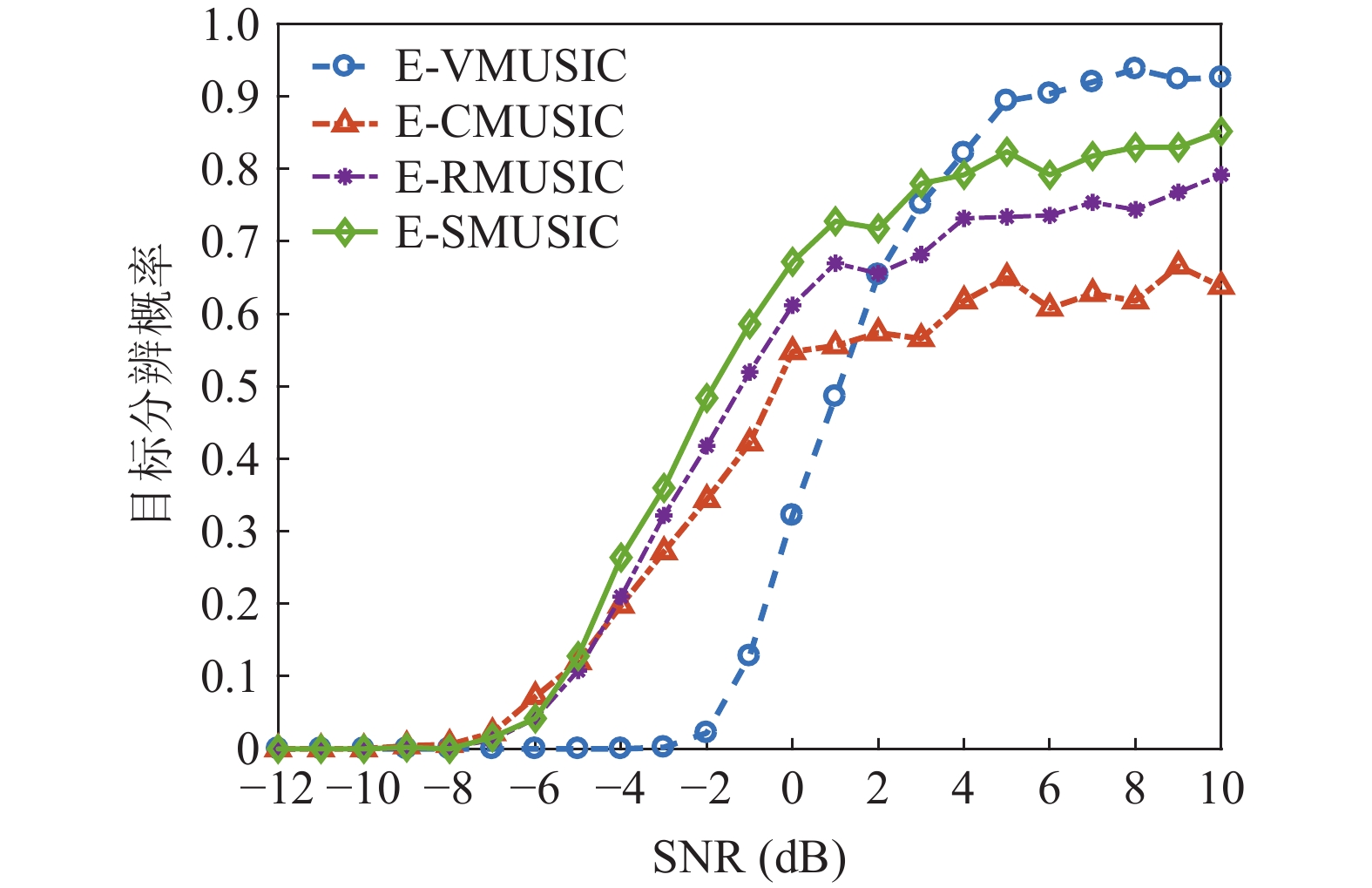
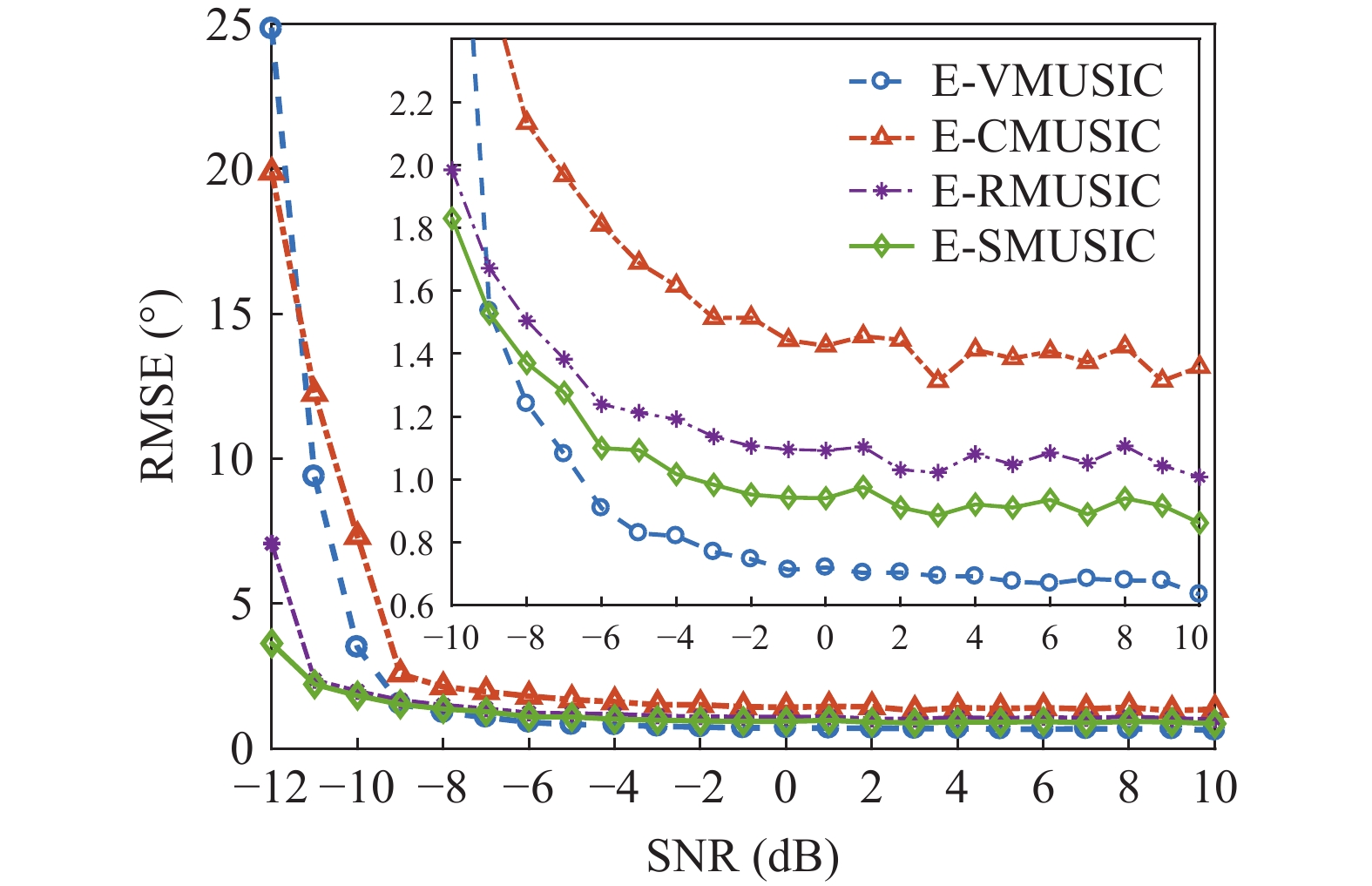
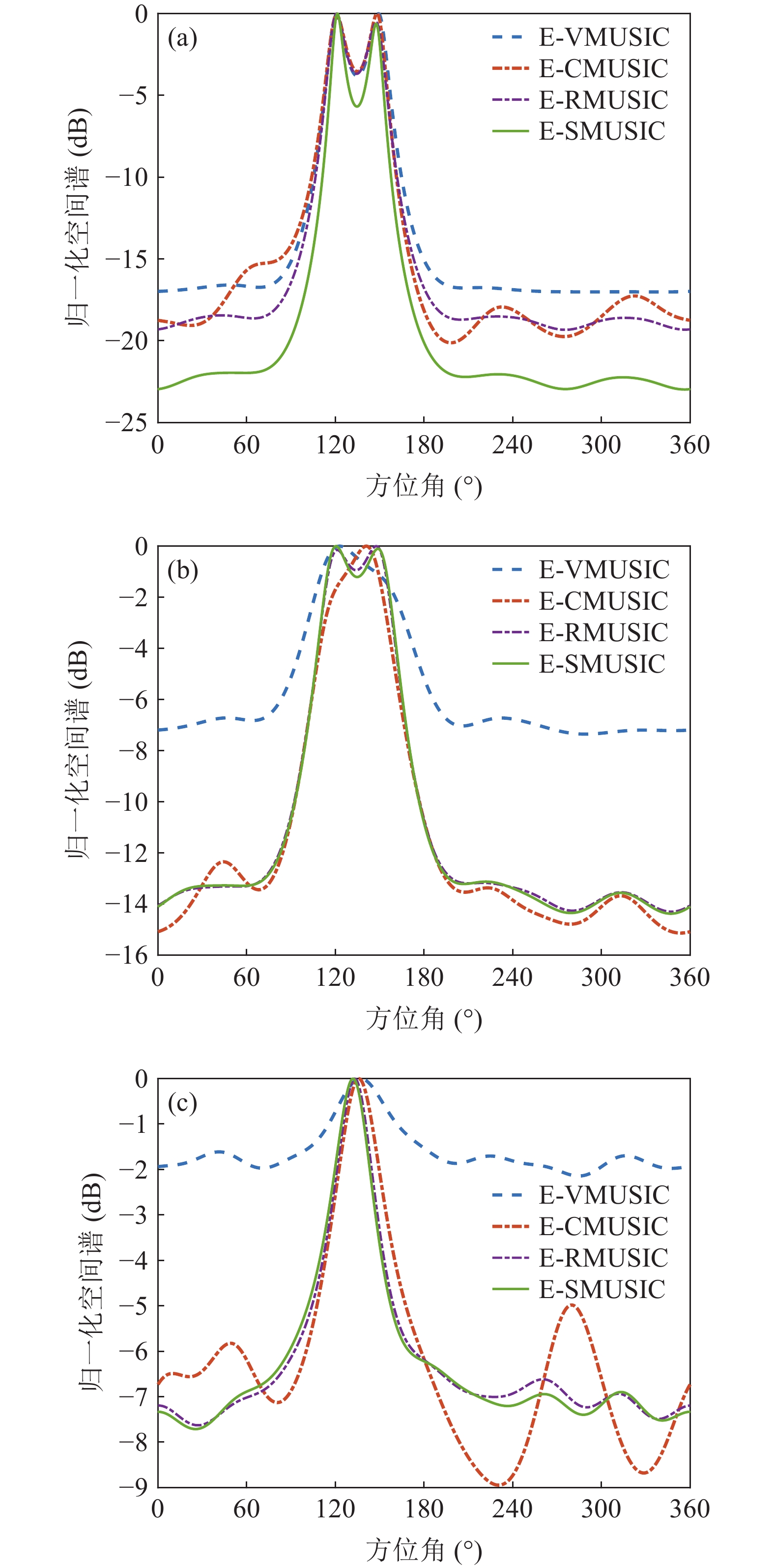
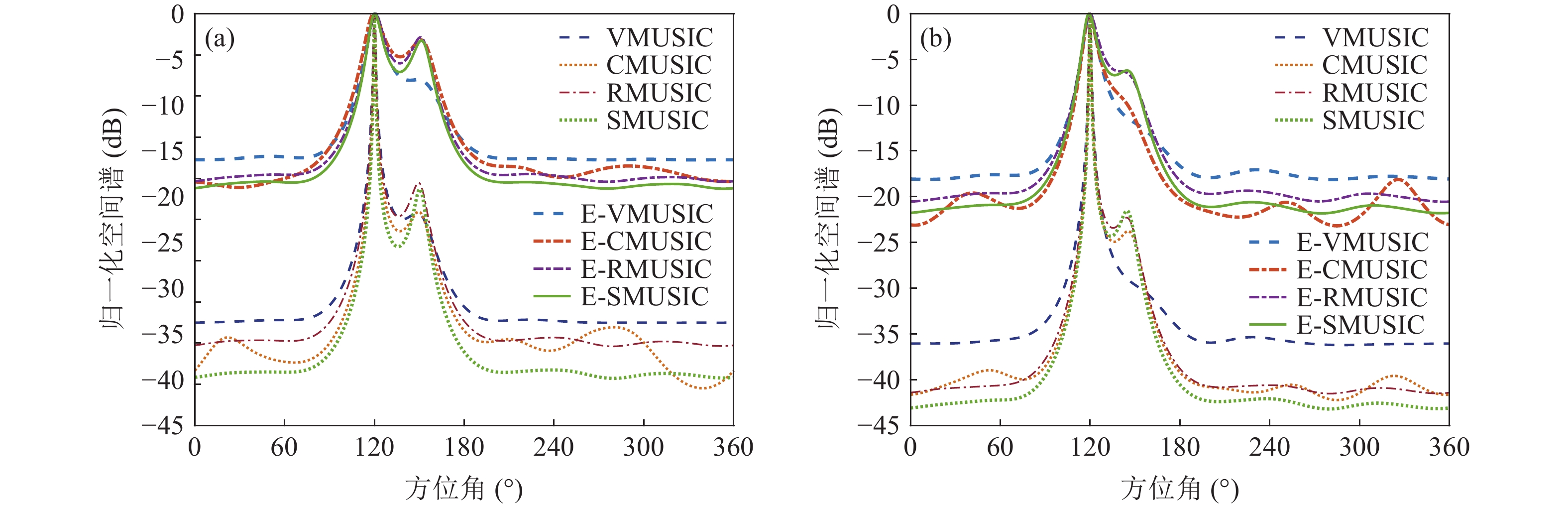
{v_x},{v_y} 通道的幅相误差统计独立, 其中各通道增益误差均服从均值为零、方差为\sigma _g^2 的高斯分布, 各通道相位误差均服从均值为零、方差为\sigma _\phi ^2 的高斯分布。假设各通道增益误差标准差{\sigma _g} = 0.1 , 相位误差标准差{\sigma _\phi } = {5{\text{°}} } , 快拍数2000, 两信源方位角分别为120°和 150°。图9是信噪比为0 dB, −10 dB, −15 dB 时, 无幅相误差和经500次蒙特卡罗实验得到的存在幅相误差的4种方法的空间谱图, 其中存在幅相误差的图例带有‘E-’前缀。由图9可知, 幅相误差对归一化空间谱影响显著, 4种方法空间谱谱峰变宽, 背景级均有不同程度的明显抬高; 幅相误差影响下, E-SMUSIC方法仍比其他3种方法背景级更低、谱峰更尖锐, 且较高信噪比(0 dB)时优势更为明显, E-RMUSIC和E-CMUSIC空间谱相仿; 低信噪比条件下, 声压振速联合处理更具优势, 存在幅相误差的E-CMUSIC、E-RMUSIC和E-SMUSIC方法的背景谱低于无幅相误差的VMUSIC背景谱; 信噪比为−10 dB时, E-VMUSIC方法两信源谱峰已完全混叠, 而E-RMUSIC和E-SMUSIC方法仍能够较为明显地分辨出两信源; 信噪比为−15 dB时, 4种MUSIC方法均无法分辨两信源, 但E-SMUSIC的空间谱具有最低的背景级。3.2.2 目标分辨能力
假设两信源方位角分别为120°和135°, 以验证幅相误差影响下4种MUSIC方法分辨两方位相近信源的能力。假设各通道增益误差标准差
{\sigma _g} = 0.1 , 相位误差标准差{\sigma _\phi } = {5{\text{°}} } , 快拍数2000, 信噪比−12~10 dB, 扫描角度间隔0.5°。图10为幅相误差影响下目标分辨概率随信噪比变化情况, 随着信噪比增大4种方法的目标分辨概率整体上均有上升, 但幅相误差导致4种方法的目标分辨能力较图5显著下降。其中E-SMUSIC、E-RMUSIC和E-CMUSIC方法在低信噪比条件下较E-VMUSIC的目标分辨能力更优, 这是由VMUSIC主瓣宽度限制导致的, 随着信噪比增大至3 dB以上, E-VMUSIC方法超过其他方法稳定在0.95附近, 而3种声压振速联合处理MUSIC方法曲线趋势相似, E-SMUSIC、E-RMUSIC和E-CMUSIC方法目标分辨概率分别稳定在0.85, 0.75, 0.65左右。3.2.3 方位估计精度
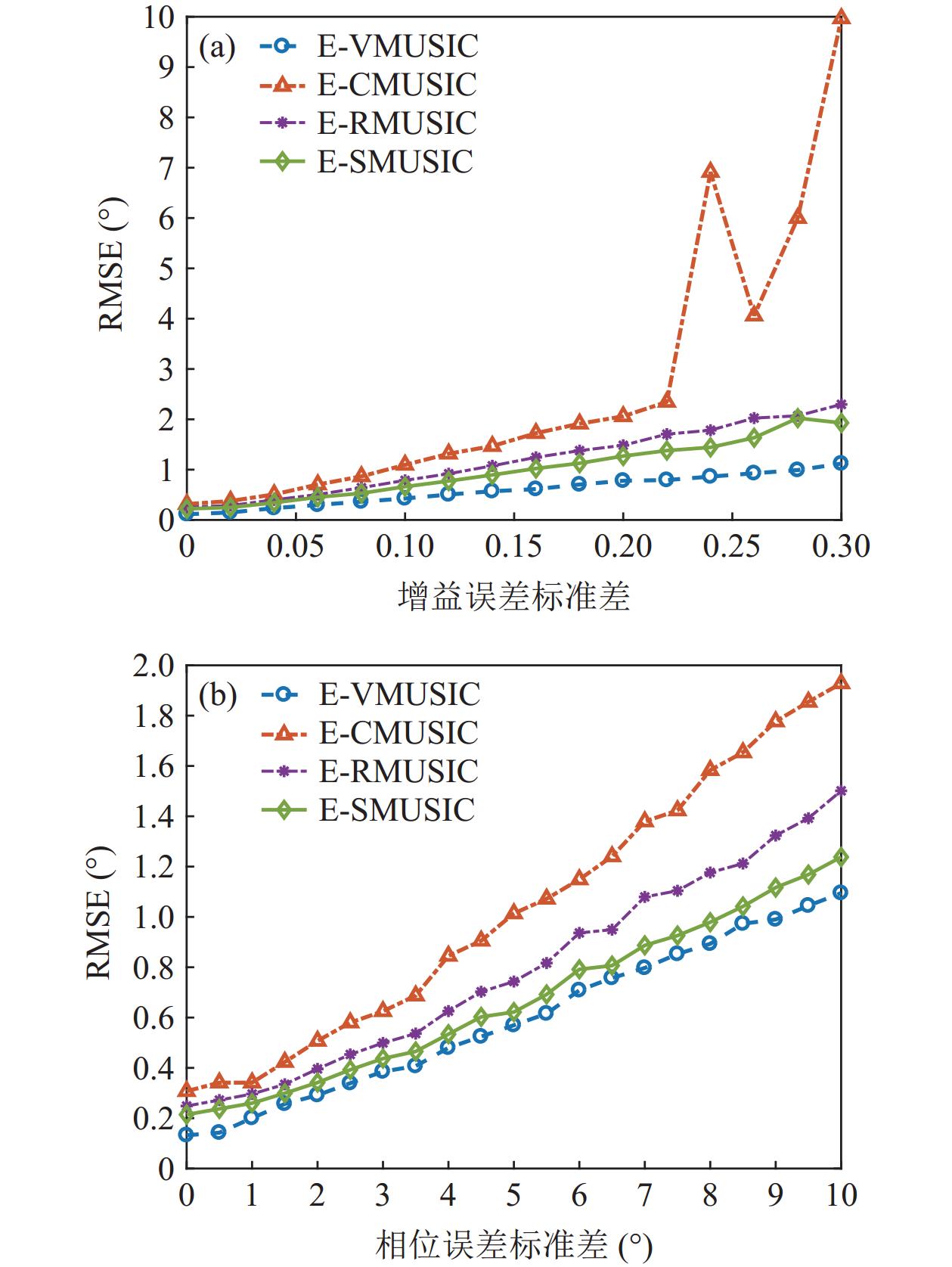
假设两信源方位角分别为120°和160°, 以验证幅相误差影响下4种MUSIC方法的方位估计精度。假设信噪比0 dB, 快拍数2000, 扫描角度间隔0.5°, 图11(a)(b)分别为4种方法DOA估计结果的均方根误差随增益误差标准差
{\sigma _g} 和相位误差标准差{\sigma _\phi } 变化的情况, 图11(a)中{\sigma _\phi } = {0{\text{°}} } ,{\sigma _g} = 0:0.02:0.3 , 图11(b)中{\sigma _g} = {0^\circ } ,{\sigma _\phi } = {0{\text{°}} }:{0.5{\text{°}} }:{10{\text{°}} } 。受增益误差和相位误差影响, 4种方法的均方根误差整体上均有不同程度的增加, 但规律相同, 即SMUSIC和RMUSIC方法具有比CMUSIC更优的方位估计精度, 而逊色于VMUSIC方法; 图11(a)中E-CMUSIC方法在增益误差标准差{\sigma _g} 大于0.2后均方根误差剧烈增加, 可能是较大增益误差使两信源未能成功分辨导致的。假设快拍数2000, 信噪比−12~10 dB, 扫描角度间隔0.5°。图12为增益误差标准差
{\sigma _g} = 0.1 , 相位误差标准差{\sigma _\phi } = {5{\text{°}} } 时, DOA估计结果的均方根误差随信噪比变化情况。随着信噪比的增大, 4种方法的均方根误差整体上均有所下降; 声压振速联合处理方法中, E-SMUSIC方法的方位估计精度最优, E-RMUSIC次之, E-CMUSIC最差。较高信噪比条件下, E-VMUSIC方法的方位估计精度优于其他3种方法, 但受幅相误差影响, 4种方法均难以实现对两信源的精准估计, 始终存在一定误差, 其中E-VMUSIC、E-SMUSIC、E-RMUSIC和E-CMUSIC方法的均方根误差在信噪比大于−4 dB后分别稳定在0.7°, 0.9°, 1.1°, 1.4°附近; 信噪比低于−9 dB时, E-VMUSIC方法的均方根误差依次超过E-SMUSIC、E-RMUSIC, 可见即便存在一定幅相误差, 改进的MUSIC方法在低信噪比条件下的方位估计精度仍有一定优势。3.3 噪声相关性影响分析
3.3.1 空间谱
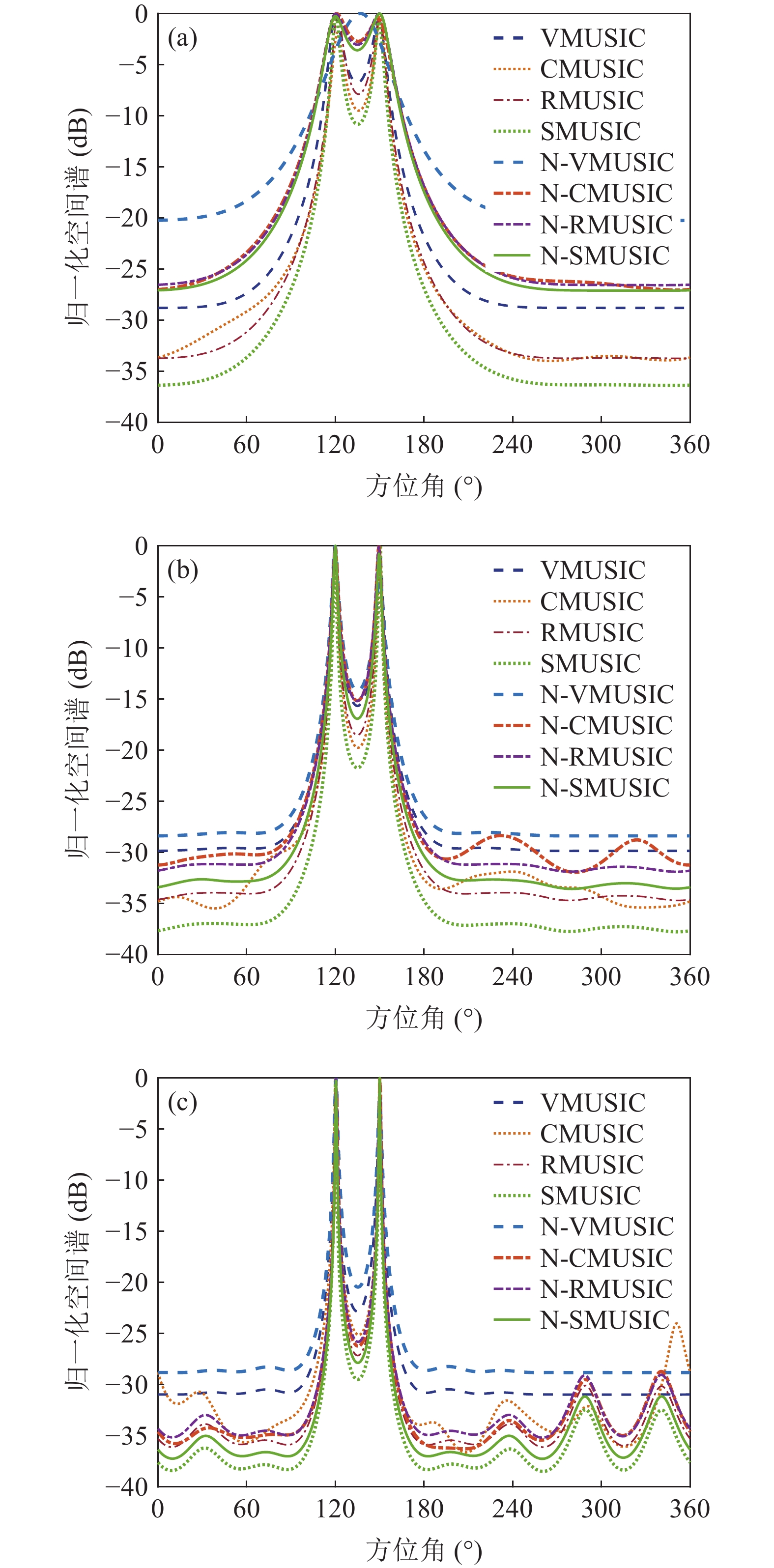
考虑声矢量圆阵各通道噪声的相关性, 假设背景噪声为各向同性噪声, 信噪比0 dB, 快拍数2000, 两信源方位角分别为120°和150°, 图13(a)(b)(c)分别为圆阵半径
{{r = \lambda} \mathord{\left/ {\vphantom {{r = \lambda} 4}} \right. } 4},{{{\text{ }}\lambda} \mathord{\left/ {\vphantom {{{\text{ }}\lambda} 2}} \right. } 2},{{{\text{ }}3\lambda} \mathord{\left/ {\vphantom {{{\text{ }}3\lambda} 4}} \right. } 4} 时, 各通道噪声不相关和考虑噪声相关性的4种MUSIC方法的空间谱图, 其中考虑噪声相关性的图例带有‘N-’前缀。在噪声较高相关({{r = \lambda} \mathord{\left/ {\vphantom {{r = \lambda} 4}} \right. } 4} )条件下, 4种方法的空间谱谱峰变宽、背景级明显抬高, 其中噪声相关性对N-VMUSIC方法影响显著, 其空间谱两信源谱峰混叠; 随着声矢量圆阵阵列孔径增加, 4种方法空间谱谱峰变窄, 但不相关噪声条件下由于信噪比给定, 其背景级变化不大; 随着各通道噪声相关性的减弱, 考虑噪声相关性时4种方法的空间谱与其对应的不相关噪声条件的空间谱逐渐接近, 其中N-SMUSIC方法仍比其他3种方法背景级更低、谱峰更尖锐, N-RMUSIC与N-CMUSIC的背景级相近, 但背景起伏更平坦, 而N-VMUSIC方法背景级最高、谱峰最宽, 且受噪声相关性影响最大。3.3.2 目标分辨能力
假设背景噪声为各向同性噪声, 声矢量圆阵半径
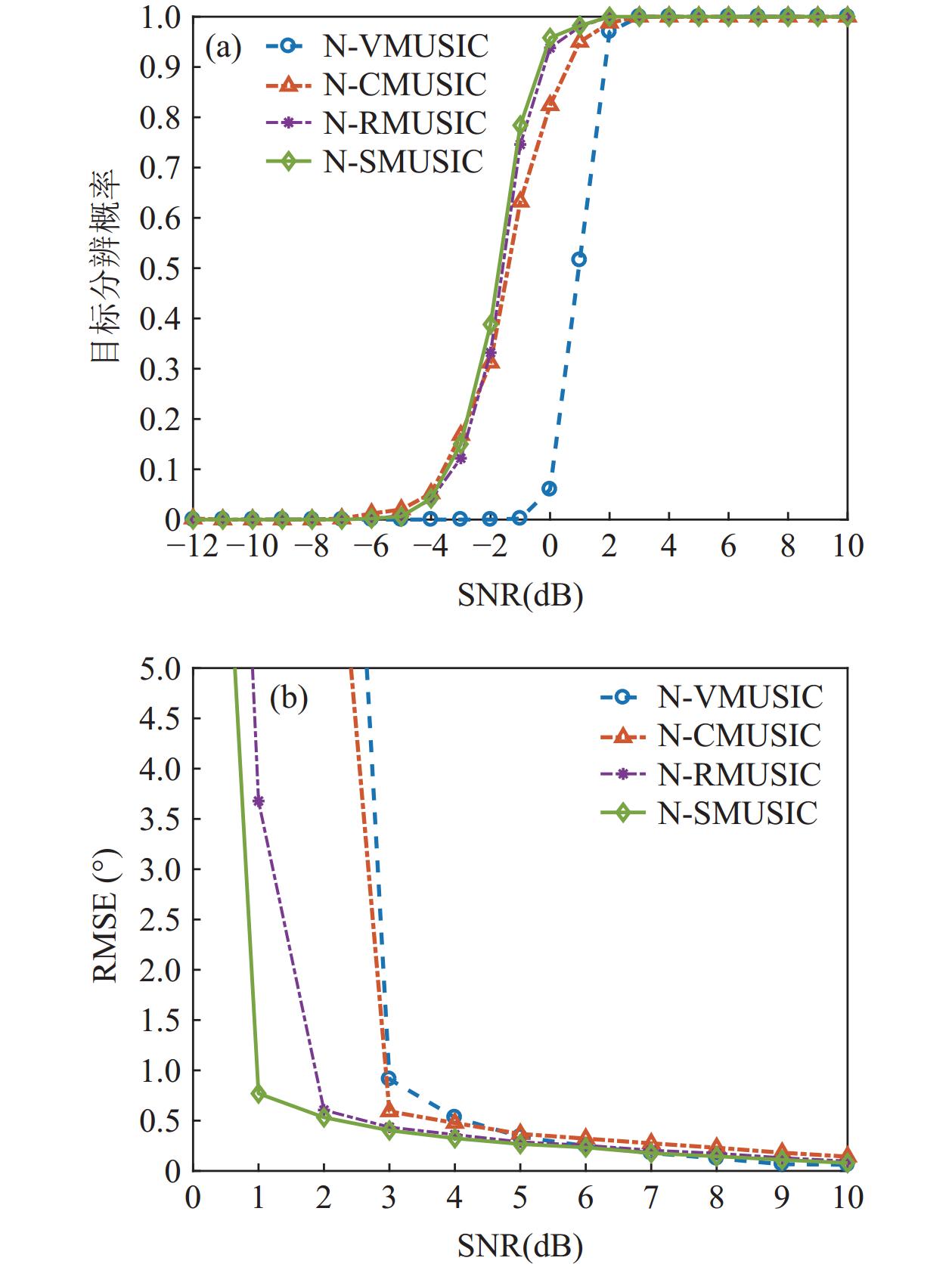
{{r = \lambda} \mathord{\left/ {\vphantom {{r = \lambda} 2}} \right. } 2} , 两信源方位角分别为120°和135°, 信噪比−12~10 dB, 快拍数2000, 扫描角度间隔0.5°。图14(a)(b)分别为各向同性噪声条件下4种MUSIC方法DOA估计结果的目标分辨概率和均方根误差随信噪比的变化情况。4种方法对两方位相近信源的分辨能力整体上较图6中噪声不相关情况明显变差, 但噪声相关性影响下, N-RMUSIC和N-SMUSIC的目标分辨能力仍优于N-VMUSIC和N-CMUSIC方法。3.3.3 方位估计精度
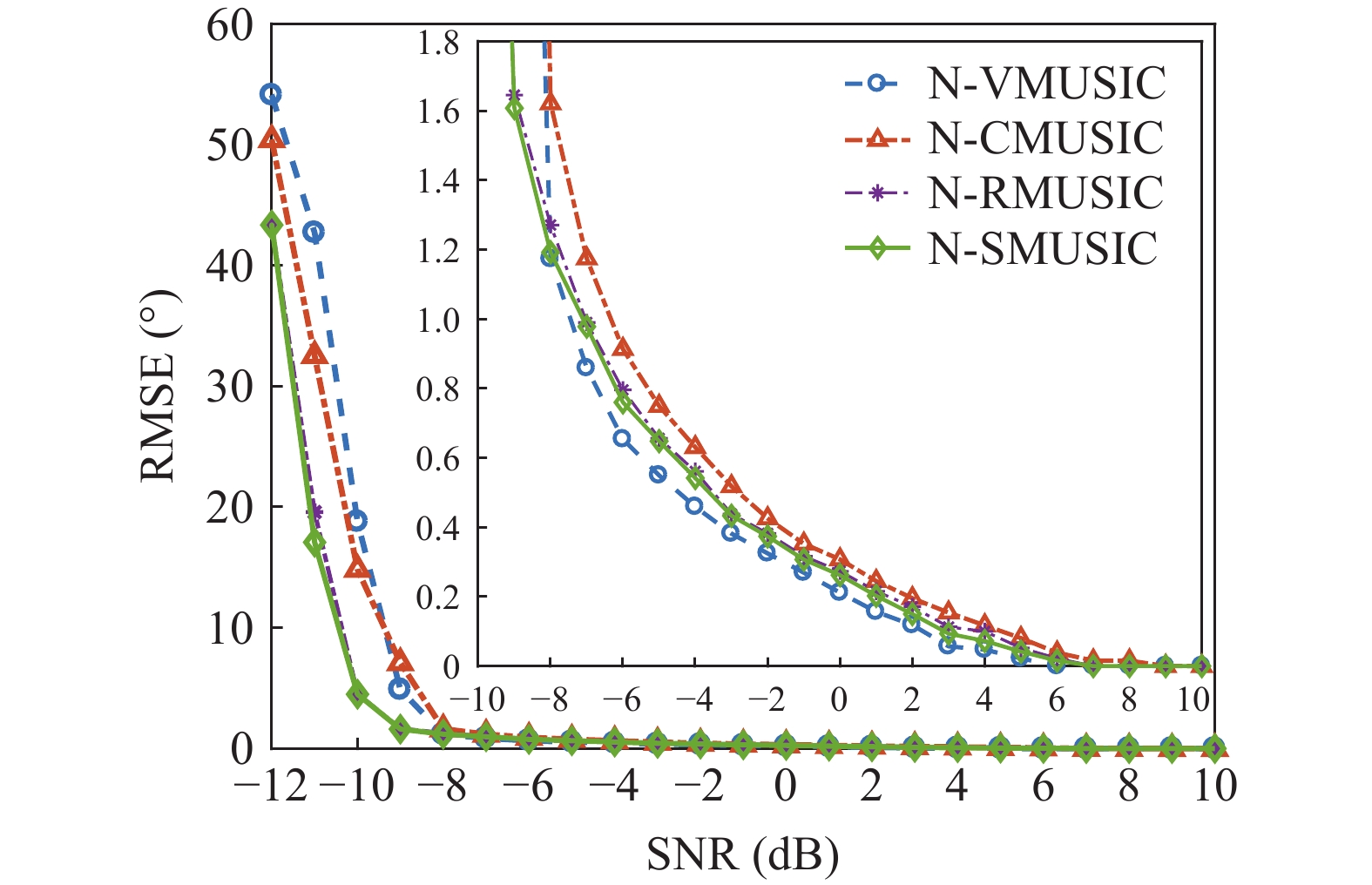
假设背景噪声为各向同性噪声, 声矢量圆阵半径
{{r = \lambda} \mathord{\left/ {\vphantom {{r = \lambda} 2}} \right. } 2} , 两信源方位角分别为120°和160°, 信噪比−12~10 dB, 快拍数2000, 扫描角度间隔0.5°。图15为噪声相关性影响下4种MUSIC方法DOA的均方根误差随信噪比变化情况。4种方法的均方根误差整体上较图8噪声不相关情况均有所下降, 但随信噪比变化的规律与其相同, 即N-RMUSIC和N-SMUSIC方法的均方根误差接近, 均优于N-CMUSIC, 而N-VMUSIC较其他3种方法的方位估计精度最优, 但在信噪比低于−8 dB条件下方位估计性能迅速恶化。3.4 复杂场景仿真分析
3.4.1 各向同性噪声条件下存在幅相误差的空间谱
假设背景噪声为各向同性噪声, 声矢量圆阵半径
{{r = \lambda} \mathord{\left/ {\vphantom {{r = \lambda} 2}} \right. } 2} , 其声压和振速{v_x},{\text{ }}{v_y} 通道的幅相误差统计独立, 均服从零均值的高斯分布, 其中各通道增益误差标准差{\sigma _g} = 0.1 , 相位误差标准差{\sigma _\phi } = {5{\text{°}} } , 假设快拍数2000, 两信源方位角分别为120°和150°。图16(a)(b)分别为信噪比为0 dB, −10 dB, −15 dB时存在幅相误差的4种MUSIC方法的空间谱图。信噪比为0 dB时4种方法均能分辨出两信源谱峰, 其中E-SMUSIC较其他3种方法背景谱更低、主瓣宽度更窄; 信噪比为−10 dB时, E-VMUSIC与E-CMUSIC方法两信源谱峰混叠, 而E-RMUSIC和E-SMUSIC方法仍能较好地分辨出两信源谱峰; 信噪比为−15 dB时, 4种MUSIC方法均无法分辨两信源, 但E-RMUSIC和E-SMUSIC方法较E-CMUSIC方法的背景谱更平坦。3.4.2 强/弱双目标空间谱
假设声矢量圆阵半径
{{r = \lambda} \mathord{\left/ {\vphantom {{r = \lambda} 2}} \right. } 2} , 两信源信噪比分别为5 dB和-10 dB, 方位角分别为120°和150°, 声压和振速{v_x},{\text{ }}{v_y} 通道的幅相误差统计独立, 均服从零均值的高斯分布, 其中各通道增益误差标准差{\sigma _g} = 0.1 , 相位误差标准差{\sigma _\phi } = {5{\text{°}} } , 快拍数2000。图17(a)(b)分别为各通道噪声不相关和考虑噪声相关性的4种MUSIC方法的空间谱图, 其中存在幅相误差的图例带有‘E-’前缀。较强功率信源有更高的空间谱谱峰, 图17(a)中无幅相误差时, 尽管较弱功率信源的谱峰较低, 但VMUSIC方法空间谱的弱信源与强信源的谱峰并未完全混叠; 而存在幅相误差时, E-VMUSIC方法的弱信源谱峰难以辨别, E-CMUSIC能够分辨强/弱的双目标, 但E-RMUSIC和E-SMUSIC方法具有更平坦的空间谱背景级, 且对强/弱的双目标的分辨更为明显。图17(b)中背景噪声为各向同性噪声, VMUSIC的弱目标谱峰湮没于强目标谱峰空间谱中, 但其他3种方法仍能够分辨强/弱的双目标; 而存在幅相误差时, 仅有E-SMUSIC方法的弱目标谱峰较为明显。4. 湖试数据验证
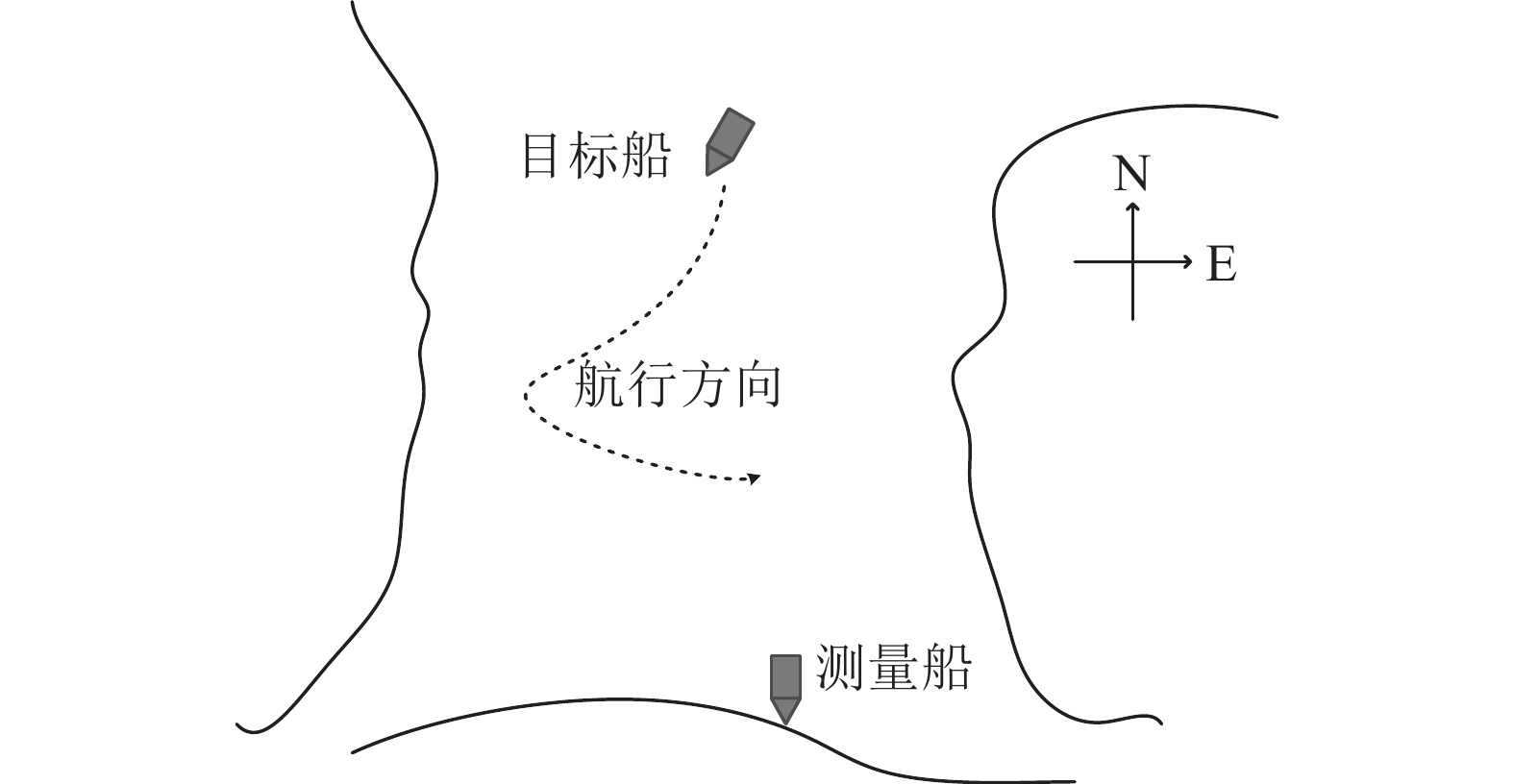
利用吉林松花湖声矢量圆阵运动目标测向试验数据验证4种MUSIC方法。试验所用声矢量圆阵由8元声矢量传感器组成, 半径为0.3 m, 矢量传感器两振速通道分别沿圆阵的径向和切向布放, 通过将其投影到
x,{\text{ }}y 轴以保证与1.1节模型一致。将声矢量圆阵布放于较为开阔的水域, 布放点处水深约22 m, 声矢量圆阵入水深度为10 m, 信号通过电缆传输到测量船, 圆阵距测量船船尾约250 m。系统工作频带为100 Hz~5.3 kHz, 采样频率为131 kHz。目标船从240°方位附近向声矢量圆阵方向做“之”字形机动, 航迹如图18中虚线所示。图19为VMUSIC、CMUSIC、RMUSIC和SMUSIC方法的方位–时间历程图, 其积分时间为0.5 s, 设置观测方位为215°。4种方法轨迹大体一致, 其中VMUSIC方法方位历程图背景谱级较高, 轨迹最粗, 这除受低信噪比条件和模型误差影响外, 实际环境中各向异性噪声成分也可能影响了MUSIC算法的分辨能力; CMUSIC、RMUSIC和SMUSIC方法由于同时利用了
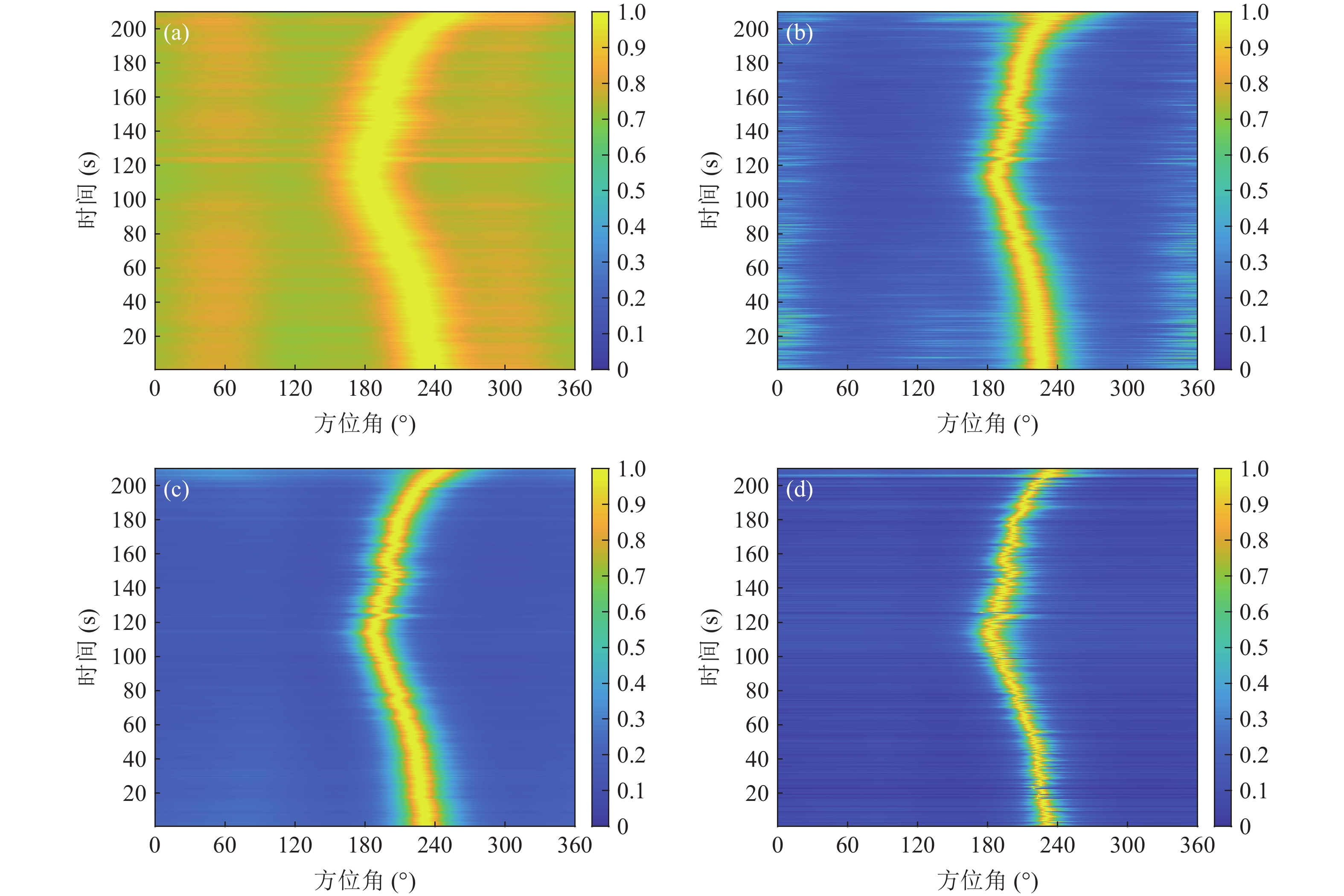
\left( {p{\text{ + }}{v_c}} \right){v_c} 指向性增益与声压振速空间相关特性的抗噪能力, 目标分辨力更高, 目标轨迹更细; RMUSIC和SMUSIC方法在CMUSIC基础上, 对协方差矩阵的分解方式做进一步改进, 保证了子空间各列向量的正交性, 体现在RMUSIC的背景级与CMUSIC接近, 但消除了CMUSIC空间谱中的伪峰, SMUSIC较CMUSIC的背景谱更低、谱峰更窄, 目标运动轨迹更为明显。图20为第50, 100, 150, 200秒时4种MUSIC方法的空间谱图。不同时刻目标方位有所区别, 但同一时刻4种方法的方位估计结果大体一致。整体上4种MUSIC方法空间谱的性能呈现出相同的规律, 即VMUSIC空间谱背景级最高、谱峰最宽, RMUSIC和CMUSIC的背景级接近但更为平坦, SMUSIC方法主瓣宽度明显较其他3种MUSIC方法相对更窄, 背景谱更低且更为平坦, 空间谱增益更高。
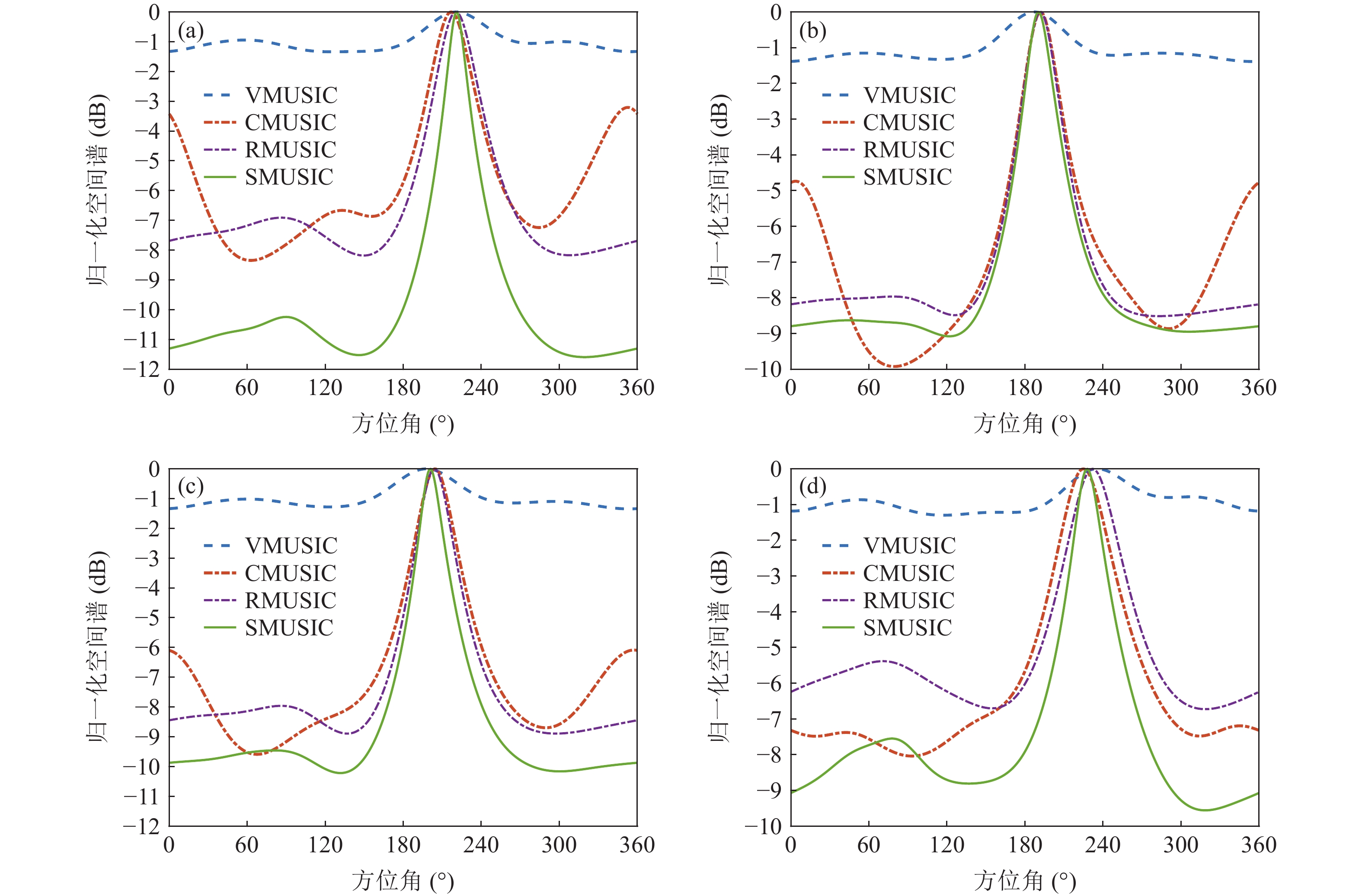
利用不同时间段合成的双目标数据验证4种MUSIC方法的目标分辨能力, 图21(a)(b)分别为利用第0秒、第100秒的合成数据和第50秒、第100秒的合成数据时, 4种MUSIC方法的空间谱图。从方位–时间历程图可知, 第0秒、第50秒时方位角分别处于240°, 220°附近, 第100秒时运动目标方位角约为190°。图21(a)中两目标方位间隔约50°, 由于目标船由远及近向声矢量圆阵机动, 第100秒目标强度略高于第0秒, 与VMUSIC、CMUSIC方法相比, 改进的MUSIC方法能够明显分辨出两目标。图21(b)中两目标方位间隔约30°, 两时刻接近, 双目标强弱相当, 此时改进的MUSIC方法依旧表现出更优的目标分辨力。
5. 结论
本文研究了模型误差条件下声矢量圆阵声压振速联合处理协方差矩阵的非正规性以及MUSIC方法的DOA估计性能, 分析了MUSIC方法DOA估计性能恶化原因, 提出了基于奇异值分解的声压振速联合处理MUSIC改进方法, 并进行了性能分析与湖试验证, 得到如下结论:
(1) 阵列响应、噪声协方差矩阵等模型误差对声压振速联合处理协方差矩阵正规性均有影响。其中, 阵列响应误差导致信号协方差矩阵的非正规性, 而有限快拍数会导致噪声协方差矩阵的非正规, 非正规矩阵不同特征值对应的特征向量不再相互正交, 导致模型误差下声压振速联合处理MUSIC方法性能恶化。
(2) 模型误差条件下MUSIC改进方法对非正规协方差矩阵进行奇异值分解, 根据奇异向量自身不同列向量之间的正交性, 利用左、右奇异向量张成噪声子空间, 在理想情况下改进方法与传统MUSIC方法性能相当, 但在模型误差条件下, 改进方法的方位估计精度和多目标分辨力均得到了提升。其中采用左、右奇异向量联合方式, 较仅利用右奇异向量具有更优的性能。
-
-
[1] Cao J, Liu J, Wang J, et al. Acoustic vector sensor: Reviews and future perspectives. IET Signal Process., 2017; 11(1): 1−9 DOI: 10.1049/iet-spr.2016.0111
[2] 张君, 陈志菲, 常继红, 等. 声矢量锥形阵的高阶累积量波达方向估计. 声学学报, 2019; 44(6): 970−985 DOI: 10.15949/j.cnki.0371-0025.2019.06.003 [3] Amir W. Blind direction-of-arrival estimation in acoustic vector-sensor arrays via tensor decomposition and Kullback-Leibler divergence covariance fitting. IEEE Trans. Signal Process., 2021; 69: 531−545 DOI: 10.1109/TSP.2020.3043814
[4] 白兴宇, 姜煜, 赵春晖. 基于声压振速联合处理的声矢量阵信源数检测与方位估计. 声学学报, 2008; 33(1): 56−61 DOI: 10.15949/j.cnki.0371-0025.2008.01.011 [5] 姚直象, 胡金华, 姚东明. 基于多重信号分类法的一种声矢量阵方位估计算法. 声学学报, 2008; 33(4): 305−309 DOI: 10.15949/j.cnki.0371-0025.2008.04.002 [6] 姚直象, 胡金华, 姜可宇. 矢量阵两类阵处理方法研究. 兵工学报, 2012; 33(9): 1138−1142 DOI: 10.3969/j.issn.1000-1093.2012.09.020 [7] Shi S, Li Y, Yang D, et al. DOA estimation of coherent signals based on the sparse representation for acoustic vector-sensor arrays. Circuits Syst. Signal Process., 2020; 39: 3553−3573 DOI: 10.1007/s00034-019-01323-7
[8] 向悠扬, 惠娟, 郭嘉宾, 等. 声矢量阵联合信息处理的信源数估计算法. 哈尔滨工程大学学报, 2022; 43(5): 706−712 DOI: 10.11990/jheu.202009050 [9] Schmidt R O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag., 1986; 34(3): 276−280 DOI: 10.1109/TAP.1986.1143830
[10] Nehorai A, Paldi E. Acoustic vector-sensor array processing. IEEE Trans. Signal Process., 1994; 42(9): 2481−2491 DOI: 10.1109/78.317869
[11] Stoica P, Nehorai A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process., 1989; 37(5): 720−741 DOI: 10.1109/29.17564
[12] 刘凯, 梁国龙, 张光普, 等. 初探阵列误差对矢量阵波束形成系统的影响. 系统仿真学报, 2012; 24(4): 848−853 [13] Hamza R, Buckley K. An analysis of weighted eigenspace methods in the presence of sensor errors. IEEE Trans. Signal Process., 1995; 43(5): 1140−1150 DOI: 10.1109/78.382399
[14] 罗家洪, 方卫东. 矩阵分析引论. 广州: 华南理工大学出版社, 2006: 34−39 [15] Swindlehurst A L, Kailath T. A performance analysis of subspace-based methods in the presence of model errors. I. The MUSIC algorithm. IEEE Trans. Signal Process., 1992; 40(7): 1758−1774 DOI: 10.1109/78.143447
[16] Vincent F, Pascal F, Olivier B. A bias-compensated MUSIC for small number of samples. Signal Process., 2017; 138(3): 117−120 DOI: 10.1016/j.sigpro.2017.03.015
[17] Xu X L, Buckley K M. Bias analysis of the MUSIC location estimator. IEEE Trans. Signal Process., 1992; 40(10): 2559−2569 DOI: 10.1109/78.157296
[18] Ferreol A, Larzabal P, Viberg M. On the asymptotic performance analysis of subspace DOA estimation in the presence of modeling errors: case of MUSIC. IEEE Trans. Signal Process., 2006; 54(3): 907−920 DOI: 10.1109/TSP.2005.861798
[19] Weiss A J, Friedlander B. Effects of modeling errors on the resolution threshold of the MUSIC algorithm. IEEE Trans. Signal Process., 1994; 42(6): 1519−1526 DOI: 10.1109/78.286967
[20] Shi S, Li Y, Zhu Z, et al. Real-valued robust DOA estimation method for uniform circular acoustic vector sensor arrays based on worst-case performance optimization. Appl. Acoust., 2019; 148: 495−502 DOI: 10.1016/j.apacoust.2018.12.014
[21] 尹小艳, 杨丹丹. 关于矩阵奇异值的若干性质. 高等数学研究, 2021; 24(1): 56−58 DOI: 10.3969/j.issn.1008-1399.2021.01.017 [22] 王逸林, 赵羽, 蔡平. 矢量阵组合增益仿真分析. 声学技术, 2004; 23(Z1): 219−221 DOI: 10.3969/j.issn.1000-3630.2004.z1.067 [23] Stoica P, Nehorai A. Comparative performance study of element-space and beam-space MUSIC estimators. Circuits Syst. Signal Process., 1991; 10(3): 285−292 DOI: 10.1007/BF01187547
[24] Lee H B, Wengrovitz M S. Resolution threshold of beamspace MUSIC for two closely spaced emitters. IEEE Trans. Acoust. Speech Signal Process., 1990; 38(9): 1545−1559 DOI: 10.1109/29.60074
-
期刊类型引用(0)
其他类型引用(1)



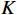
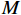

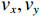
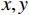
 下载:
下载: