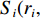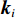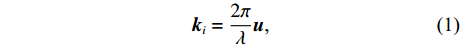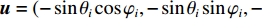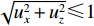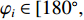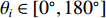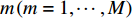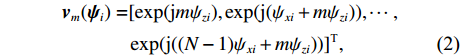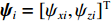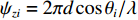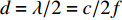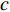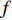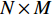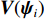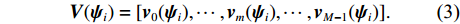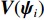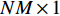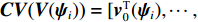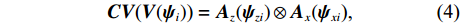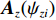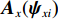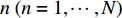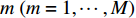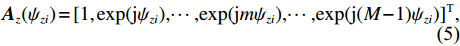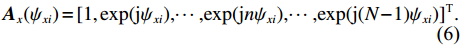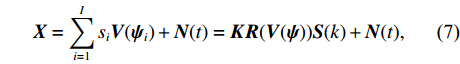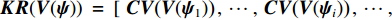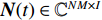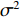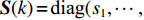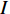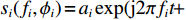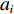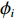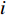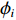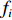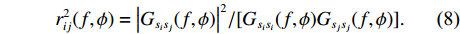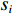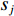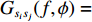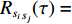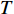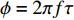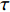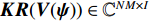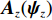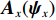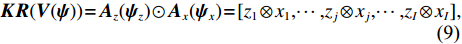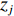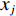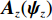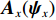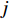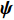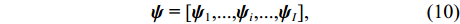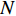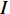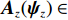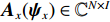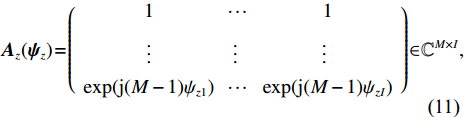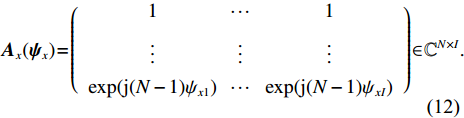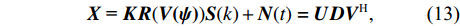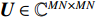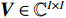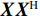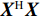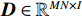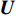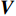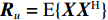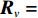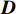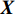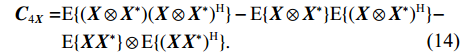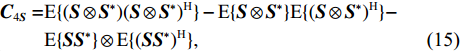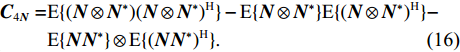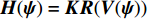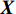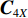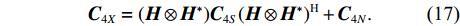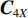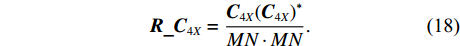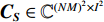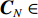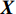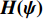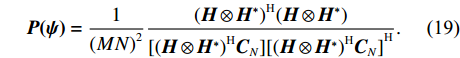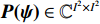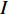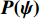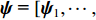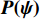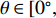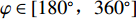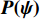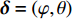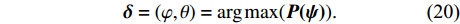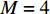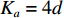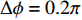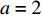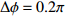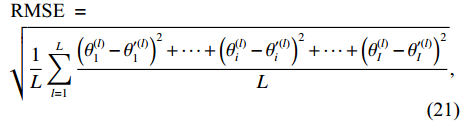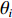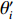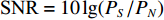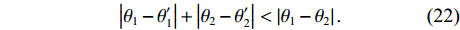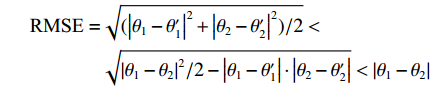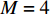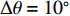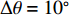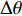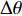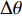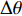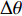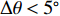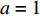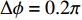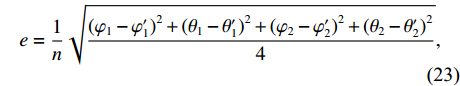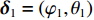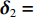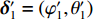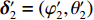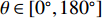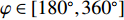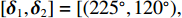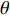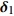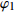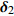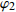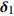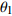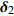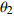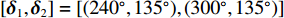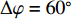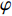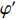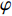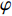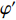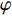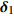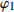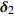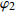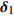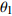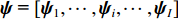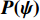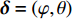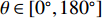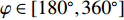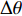Fourth-order cumulant multiple matrix reconstruction to estimate direction of arrival for coherent sound source under low signal-to-noise ratio
-
摘要:
针对相干声源子空间能量扩散且协方差矩阵欠秩难以有效估计波达方向(DOA)的问题, 提出了一种采用高阶矩阵变换的估计方法−四阶累积量多重矩阵重构(FOC-MMR)。该方法首先对阵列声压数据分帧进行短时傅里叶变换, 然后对四阶累积量扩展的高阶协方差矩阵进行奇异值分解(SVD)得到高阶噪声特征向量, 保证该噪声特征向量与扩展后的高阶阵列流形矢量正交匹配, 最终实现相干信号的DOA估计。相干单频矩形脉冲信号仿真结果表明, 将FOC-MMR方法应用于均匀线阵(ULA, M = 4), 在信噪比SNR ≥ −15 dB时, 相干信号(θ1 = −20°和θ2 = 20°)的均方根误差保持在1.5°以内; 在SNR = 10 dB时, 可正确分辨的两相干信号方位间隔
Δθ 可以低至5°。在相干脉冲声源实验中, 通过混入SNR = 5 dB高斯白噪声, 验证了FOC-MMR算法在应用于由多个ULA组成的矩形面阵时, 其分辨邻近声源和抑制高斯噪声的能力较高。FOC-MMR算法通过对声压阵列数据扩展得到满秩的高阶协方差矩阵, 不仅解决了由信号相干造成的噪声和信号特征向量之间能量扩散的问题, 还实现了以较高的测向精度和空间分辨率对广角入射的多组相干声源的DOA估计。Abstract:A direction of arrival (DOA) estimation method that adopts higher-order matrix transformation, named fourth-order cumulant multiple matrix reconstruction (FOC-MMR), is proposed to effectively estimate the DOA of the coherent sound sources which cause the subspace energy dispersion and under-rank of the covariance matrix. Firstly, short-time Fourier transform is performed on the array sound pressure data in frames. Secondly, singular value decomposition (SVD) of the fourth-order cumulant-expanded higher-order covariance matrix is calculated to obtain the higher-order noise eigenvectors, which are orthogonally matched with the expanded higher-order array manifold vector. Finally, DOA estimation of the coherent signals is achieved. The simulation results of coherent single-frequency rectangular pulse signal show that when the signal-to-noise ratio (SNR) ≥ −15 dB, applying the proposed method to the uniform linear array (ULA, M = 4), the root mean square error (RMSE) of coherent signals (θ1 = −20° and θ2 = 20°) remains within 1.5°. The correctly resolved azimuth interval
Δθ can be as low as 5° when the SNR = 10 dB. The coherent pulse sound source experiment mixed with SNR = 5 dB Gaussian white noise verifies that when applying the FOC-MMR algorithm to a rectangular area array composed of multiple ULAs, it can distinguish adjacent sound sources with a high degree of ability to suppress Gaussian noise. The proposed method achieves full-rank high-order covariance matrix by reconstructing the virtual sound pressure array data, which not only solves the problem of energy diffusion between noise and signal eigenvectors caused by signal coherence, but also the DOA estimation of multiple groups of coherent sound sources with wide-angle incidence is achieved with higher direction measurement accuracy and spatial resolution. -
引言
波达方向(DOA)估计是传声器阵列信号处理的重要研究方向。复杂声场中, 由于声源之间相互干涉造成声源相干, 进而影响DOA估计精度。针对相干声源DOA估计问题, 国内外学者主要通过研究各种阵列结构和改进DOA估计算法来解决。其中, 基于子空间的算法在估计复杂声场中邻近相干声源的DOA时, 估计效果较差。主要原因在于应用子空间法对阵列信号的欠秩协方差矩阵进行奇异值分解(SVD)[1-2]后, 得到的信号特征向量和噪声特征向量(NFV)会因能量扩散而呈现非严格正交, 从而导致由NFV与阵列流形矢量(AMV)决定的空间谱重建声场产生混叠, 无法有效估计相干信号的DOA。
根据声压数据矩阵处理过程和阵列结构不同, 基于子空间的相干声源DOA估计算法主要分为空间平滑算法[3-5]、矩阵重构算法[6-8]、最大似然估计算法[9-11]、高阶累积量重构算法[12-18]、稀疏正则化和反卷积算法[19-21]等。文献[4]利用空间平滑方法迭代运算恢复去除噪声分量后协方差矩阵的秩, 但是其计算量会随迭代次数增加而递增。文献[9]提出基于频率平滑的最大似然估计方法(FS-MLE), 通过频率平滑技术提高最大似然估计法[10]对独立或相干声源的DOA估计精度和分辨率, 当参与拟合的数据较少, 特别是SNR < 0 dB时, DOA的估计精度会有所降低; 当参与拟合的数据过多时, 则会导致运算复杂度增加。文献[12]结合最小冗余线阵(MRLA)和四阶累积量的扩展性, 通过应用四阶累积量改进波束形成方法验证了其具有更高的线阵阵列增益和噪声抑制能力。文献[13-14]分别利用高阶累积量改进多重信号分类算法(MUSIC)和旋转不变技术估计参数法(ESPRIT), 由于高阶累积量对虚拟阵列的扩展, 使得不受阵型限制[16-18]的谱估计算法可以有效抑制高斯噪声的干扰, 从而实现多个独立信号的DOA估计。然而, 当复杂声场由相干声源组成时, 研究基于高阶累积量阵列扩展得到的满秩高阶协方差矩阵是否包含所有声源信息, 对其奇异值分解(SVD)得到的高阶噪声特征向量(HO-NFV)是否正交于高阶阵列流形矢量(HO-AMV), 当信噪比较低和阵元较少时信号和噪声的特征是否能完全分离, 是保证改进MUSIC类算法能否用于相干声源DOA估计的关键。
针对低信噪比下相干声源的DOA估计, 提出了一种采用高阶矩阵变换的估计方法, 即四阶累积量多重矩阵重构(FOC-MMR), 该方法利用声信号的时频域稀疏特性[22-23]对传声器阵列信号进行多重矩阵重构。首先, 利用四阶累积量重构短时傅里叶变换(STFT)后的传声器阵列声压数据以抑制高斯噪声的干扰。然后, 对重构矩阵的协方差进行奇异值分解(SVD), 以获得能量分离的高阶信号特征向量和高阶噪声特征向量(HO-NFV)。其中, 为了对应数据重构之后的扩展阵列结构信息, 对原始AMV及其复共轭求克罗内克积以得到高阶阵列流形矢量(HO-AMV)。最后, 根据NFV和AMV的正交性计算功率谱对空间网格进行归一化空间谱(NSS)峰值搜索, 从而实现相干声源的DOA有效估计。
1. 系统模型和高阶矩阵变换方法
1.1 系统模型
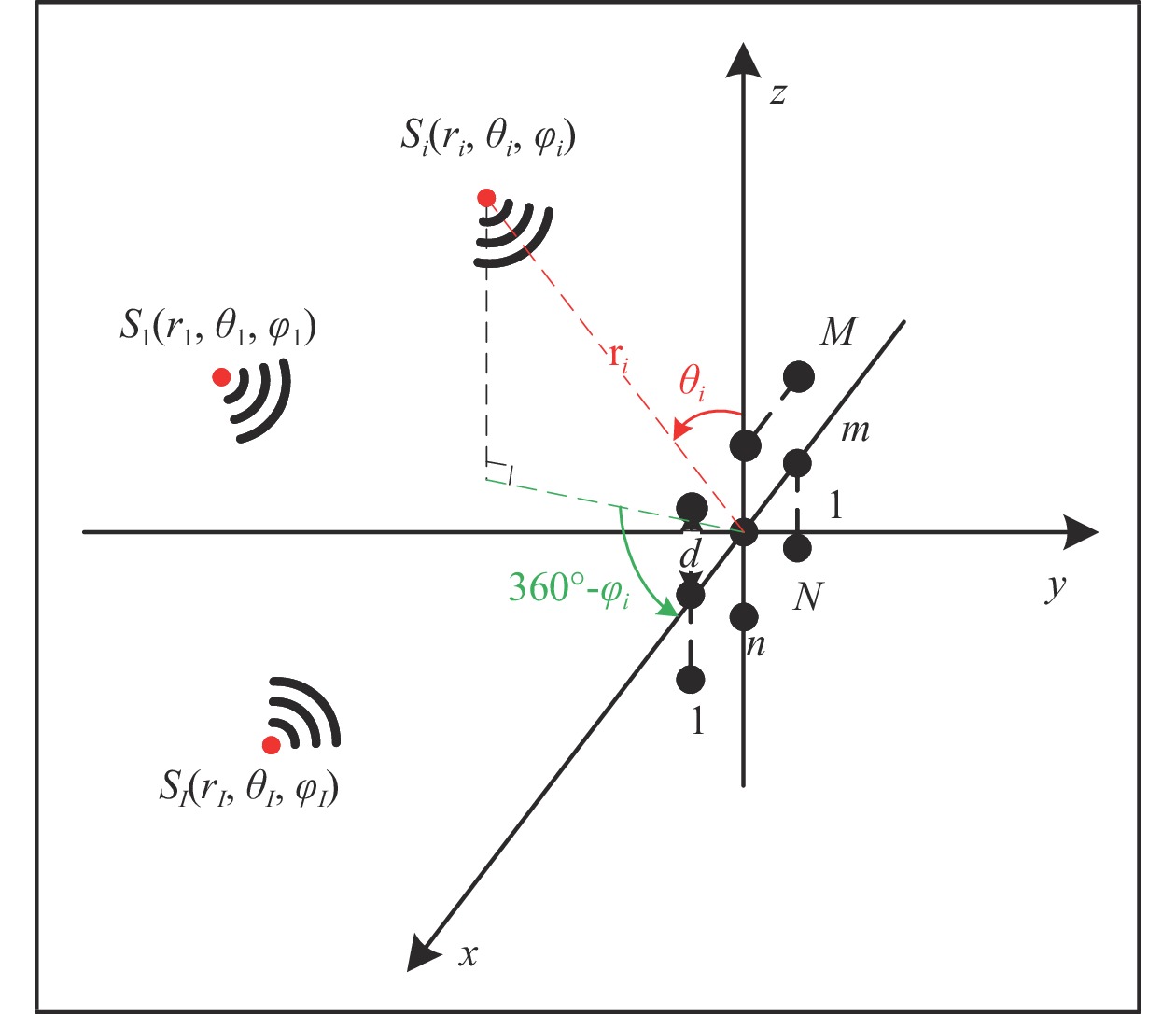
考虑在平面矩形区域均匀地布置间距为
d 的M×N 个传声器, 如图1所示。假设声场由来自距离原点{\boldsymbol{r}} = [{r_1},\cdots,{r_i},\cdots,{r_I}] 的I 个远场声源组成, 第i 个声源发出的平面波到达阵列的主要传播路径相应的仰角{\theta _i} 和方位角{\varphi _i} , 相应的DOA表示为{{\boldsymbol{\delta}} _i} = ({\varphi _i},{\theta _i}) 。在均匀介质中传播的平面波由远场声源
{S_i}({r_i}, {\theta _i},{\varphi _i}) 生成, 定义波数{{\boldsymbol{k}}_i} 为{{\boldsymbol{k}}_i} = \frac{{2\pi }}{\lambda }{\boldsymbol{u}}{\text{,}} (1) 式中
{\boldsymbol{u}} 为单位矢量,{\boldsymbol{u}} = ( - \sin {\theta _i}\cos {\varphi _i}, - \sin {\theta _i}\sin {\varphi _i}, - \cos {\theta _i})^{\text{T}} , 阵列的可视区域为\sqrt {u_x^2 + u_z^2} \leqslant 1 , 即{\varphi }_{i}\in [180^\circ, 360^\circ] 和{\theta _i} \in [0^\circ ,180^\circ ] 。类似于线阵的AMV定义, 第
m\,(m = 1,\cdots,M) 行传声器的AMV可定义为\begin{split} {{\boldsymbol{v}}_m}({{\boldsymbol{\psi}} _i}) =& [\exp ({\text{j}}m{\psi _{zi}}),\exp ({\text{j}}({\psi _{xi}} + m{\psi _{zi}})),\cdots,\\&\exp ({\text{j}}((N - 1){\psi _{xi}} + m{\psi _{zi}}))]^{\text{T}}, \end{split} (2) 式中向量
{{\boldsymbol{\psi}} _i} = {[{\psi _{xi}},{\psi _{zi}}]^{\text{T}}} , 其中{\psi _{xi}} = 2\pi d\sin {\theta _i}\cos {\varphi _i}/\lambda ,{\psi _{zi}} = 2\pi d\cos {\theta _i}/\lambda ,d = \lambda /2 = c/2f ,c 为声音在介质中的传播速度,f 为声源的主频[24]。则N \times M 阶AMV, 即{\boldsymbol{V}}({{\boldsymbol{\psi}} _i}) 定义为{\boldsymbol{V}}({{\boldsymbol{\psi}} _i}) = [{{\boldsymbol{v}}_0}({{\boldsymbol{\psi}} _i}),\cdots,{{\boldsymbol{v}}_m}({{\boldsymbol{\psi}} _i}),\cdots,{{\boldsymbol{v}}_{M - 1}}({{\boldsymbol{\psi}} _i})]. (3) 将
{\boldsymbol{V}}({{\boldsymbol{\psi}} _i}) 改写为NM \times 1 的列向量{\boldsymbol{CV}}{\text{(}}{\boldsymbol{V}}({{\boldsymbol{\psi}} _i}){\text{)}} = [{\boldsymbol{v}}_0^{\text{T}}({{\boldsymbol{\psi}} _i}),\cdots, {\boldsymbol{v}}_m^{\text{T}}({\psi _i}),\cdots,{\boldsymbol{v}}_{M - 1}^{\text{T}}({{\boldsymbol{\psi}} _i})]^{\text{T}} , 并改写为Kroneker积的形式, 表示为{\boldsymbol{CV}}{\text{(}}{\boldsymbol{V}}({{\boldsymbol{\psi}} _i}){\text{)}} = {{\boldsymbol{A}}_z}({{\boldsymbol{\psi}} _{zi}}) \otimes {{\boldsymbol{A}}_x}({{\boldsymbol{\psi}} _{xi}}{\text{),}} (4) 式中,
{{\boldsymbol{A}}_z}({\psi _{zi}}) 和{{\boldsymbol{A}}_x}({{\boldsymbol{\psi }}_{xi}}{\text{)}} 分别表示第n{\text{ }}(n = 1,\cdots,N) 列和第m{\text{ }}(m = 1,\cdots,M) 行的传声器的AMV:{{\boldsymbol{A}}_z}({\psi _{zi}}) = {[1,\exp ({\text{j}}{\psi _{zi}}), \cdots, \exp ({\text{j}}m{\psi _{zi}}), \cdots, \exp ({\text{j}}(M - 1){\psi _{zi}})]^{\text{T}}}, (5) {{\boldsymbol{A}}_x}({\psi _{xi}}) = {[1,\exp ({\text{j}}{\psi _{xi}}), \cdots, \exp ({\text{j}}n{\psi _{xi}}), \cdots, \exp ({\text{j}}(N - 1){\psi _{xi}})]^{\text{T}}}. (6) 传声器阵列接收到的阵列信号数据可表示为矩阵形式:
{\boldsymbol{X}} = \sum\limits_{i = 1}^I {{s_i}{\boldsymbol{V}}({{\boldsymbol{\psi}} _i}) + {\boldsymbol{N}}(t)} = {\boldsymbol{KR}}({\boldsymbol{V}}({\boldsymbol{\psi}} )) {\boldsymbol{S}}(k) + {\boldsymbol{N}}(t), (7) 式中,
{\boldsymbol{KR}}({\boldsymbol{V}}({\boldsymbol{\psi}} )) \,\,=\,\, [\,\,\,{\boldsymbol{CV}}{\text{(}}{\boldsymbol{V}}({{\boldsymbol{\psi}} _1}){\text{)}}\,,\,\,\cdots,\,\,{\boldsymbol{CV}}{\text{(}}{\boldsymbol{V}}({{\boldsymbol{\psi}} _i}){\text{)}}\,,\,\,\cdots, {\boldsymbol{CV}}{\text{(}}{\boldsymbol{V}}({{\boldsymbol{\psi}} _I}){\text{)}}] \in {{\mathbb{C}}^{NM \times I}} 包含了阵列和信号的空间特征, 在后续的数据处理中至关重要, 因为其中包含了声源的DOA信息。{\boldsymbol{N}}(t) \in {{\mathbb{C}}^{NM \times I}} 是均值为零, 方差为{\sigma ^2} 的高斯白噪声, 且噪声与信号独立[1]。{\boldsymbol{S}}(k) = {\text{diag}}({s_1},\cdots, {s_i},\cdots ,{s_I}) \in {{\mathbb{C}}^{I \times I}} 包含I 个相干信号,{s_i}({f_i},{\phi _i}) = {a_i} \exp ({\text{j}}2\pi {f_i}t + {\phi _i}) ,{a_i} 和{\phi _i} 分别是第i 个声源的幅值和相位, 相干系数由相位{\phi _i} 和频率{f_i} 共同决定, 定义为[25-26]r_{ij}^2(f,\phi ) = {\left| {{G_{{s_i s_j}}}(f,\phi )} \right|^2}/[{G_{{s_i s_i}}}(f,\phi ){G_{{s_j s_j}}}(f,\phi )]. (8) 声源信号
{s_i} 和{s_j} 的互功率谱密度为{G_{{s_i s_j}}}(f,\phi ) = {\int}_{ - \infty }^\infty {{R_{{s_i s_j}}}} (\tau ) \exp ( - {\text{j}}2\pi f\tau ){\text{d}}\tau , 其中互相关函数{R_{{s_i}}}_{{s_j}}(\tau ) = \mathop {\lim }\limits_{T \to \infty } (1/T) {\int}_{ - T/2}^{T/2} {{s_i}(t)} {s_j}(t - \tau ){\text{d}}t ,T 为信号周期, 相位差\phi = 2\pi f\tau 由信号时延差\tau 确定[26]。式(7)中
{\boldsymbol{KR}}({\boldsymbol{V}}({\boldsymbol{\psi}} )) \in {{\mathbb{C}}^{NM \times I}} 为矩阵{{\boldsymbol{A}}_z}({{\boldsymbol{\psi}} _z}) 和{{\boldsymbol{A}}_x}({{\boldsymbol{\psi}} _x}) 的Khatri-Rao积, 表示为{\boldsymbol{KR}}({\boldsymbol{V}}({\boldsymbol{\psi}} )) = {{\boldsymbol{A}}_z}({{\boldsymbol{\psi}} _z}) \odot {{\boldsymbol{A}}_x}({{\boldsymbol{\psi}} _x}) = [{z_1} \otimes {x_1}, \cdots, {z_j} \otimes {x_j}, \cdots, {z_I} \otimes {x_I}], (9) 其中
{z_j} 和{x_j} 分别代表矩阵{{\boldsymbol{A}}_z}({{\boldsymbol{\psi}} _z}) 和{{\boldsymbol{A}}_x}({{\boldsymbol{\psi }}_x}) 的第j 列, 式(9)中包含信号源DOA数据向量{\boldsymbol{\psi }} , 并可定义为{\boldsymbol{\psi}} {\text{ = [}}{{\boldsymbol{\psi}} _1}{\text{,}}...{\text{,}}{{\boldsymbol{\psi}} _i}{\text{,}}...{\text{,}}{{\boldsymbol{\psi}} _I}{\text{],}} (10) 式中
M 行和N 列阵元对I 个源的AMV, 即{{\boldsymbol{A}}_z}({{\boldsymbol{\psi }}_z}) \in {{\mathbb{C}}^{M \times I}} 和{{\boldsymbol{A}}_x}({{\boldsymbol{\psi}} _x}) \in {{\mathbb{C}}^{N \times I}} 分别表示为{{\boldsymbol{A}}_z}({{\boldsymbol{\psi}} _z}) = \left( {\begin{array}{*{20}{c}} 1& {\cdots} &1 \\ {\vdots}& {\vdots}& {\vdots} \\ {\exp ({\text{j}}(M - 1){\psi _{z1}})}& {\cdots} &{\exp ({\text{j}}(M - 1){\psi _{zI}})} \end{array}} \right) \in {{\mathbb{C}}^{M \times I}}, (11) {{\boldsymbol{A}}_x}({{\boldsymbol{\psi}} _x}) = \left( {\begin{array}{*{20}{c}} 1& {\cdots} &1 \\ {\vdots}& {\vdots} &{\vdots} \\ {\exp ({\text{j}}(N - 1){\psi _{x1}})}& {\cdots} &{\exp ({\text{j}}(N - 1){\psi _{xI}})} \end{array}} \right) \in {{\mathbb{C}}^{N \times I}}. (12) 1.2 高阶矩阵变换方法
为了从阵列接收的信号数据中获得声源信息, 对
MN \times I 维信号矩阵加Kaiser窗[23]求STFT 表示为{\boldsymbol{X}} , 再进行奇异值分解, 式(7)可以写作:{\boldsymbol{X}}{\text{ = }}{\boldsymbol{KR}}({\boldsymbol{V(\psi )}}){\boldsymbol{S}}(k) + {\boldsymbol{N}}(t) = {\boldsymbol{UD}}{{\boldsymbol{V}}^{\text{H}}}, (13) 其中,
{\boldsymbol{U}} \in {{\mathbb{C}}^{MN \times MN}} 和{\boldsymbol{V}} \in {{\mathbb{C}}^{I \times I}} 的列向量分别是{\boldsymbol{X}}{{\boldsymbol{X}}^{\text{H}}} 和{{\boldsymbol{X}}^{\text{H}}}{\boldsymbol{X}} 的特征向量,{\boldsymbol{D}} \in {{\mathbb{R}}^{MN \times I}} 是降序排列的奇异值构成的对角矩阵。从上述定义可以看出{\boldsymbol{U}} 和{\boldsymbol{V}} 的列向量分别是信号数据协方差矩阵{{\boldsymbol{R}}_u} = {\text{E}}\{ {\boldsymbol{X}}{{\boldsymbol{X}}^{\text{H}}}\} 和{{\boldsymbol{R}}_v} = {\text{E}}\{ {{\boldsymbol{X}}^{\text{H}}}{\boldsymbol{X}}\} 的特征向量,{\boldsymbol{D}} 中奇异值与接收的信号数目和能量有关。式(13)中
{\boldsymbol{X}} 的四阶累积量矩阵可表示为[12]\begin{split} {{\boldsymbol{C}}_{4{\boldsymbol X}}} = &{\text{E}}\{ ({\boldsymbol X} \otimes {{\boldsymbol X}^*}){({\boldsymbol X} \otimes {{\boldsymbol X}^*})^{\text{H}}}\} - {\text{E}}\{ {\boldsymbol X} \otimes {{\boldsymbol X}^*}\} {\text{E}}\{ {({\boldsymbol X} \otimes {{\boldsymbol X}^*})^{\text{H}}}\} - \\& {\text{E}}\{ {\boldsymbol X}{{\boldsymbol X}^*}\} \otimes {\text{E}}\{ {({\boldsymbol X}{{\boldsymbol X}^*})^{\text{H}}}\} . \\[-10pt] \end{split} (14) 根据Kronecker积的性质, 信号和噪声的四阶累积量表示为
\begin{split} {{\boldsymbol{C}}_{4{\boldsymbol S}}} =& {\text{E}}\{ ({\boldsymbol S} \otimes {{\boldsymbol S}^*}){({\boldsymbol S} \otimes {{\boldsymbol S}^*})^{\text{H}}}\} - {\text{E}}\{ {\boldsymbol S} \otimes {{\boldsymbol S}^*}\} {\text{E}}\{ {({\boldsymbol S} \otimes {{\boldsymbol S}^*})^{\text{H}}}\} - \\& {\text{E}}\{ {\boldsymbol S}{{\boldsymbol S}^*}\} \otimes {\text{E}}\{ {({\boldsymbol S}{{\boldsymbol S}^*})^{\text{H}}}\} , \end{split} (15) \begin{split} {{\boldsymbol{C}}_{4{\boldsymbol N}}} =& {\text{E}}\{ ({\boldsymbol N} \otimes {{\boldsymbol N}^*}){({\boldsymbol N} \otimes {{\boldsymbol N}^*})^{\text{H}}}\} - {\text{E}}\{ {\boldsymbol N} \otimes {{\boldsymbol N}^*}\} {\text{E}}\{ {({\boldsymbol N} \otimes {{\boldsymbol N}^*})^{\text{H}}}\} - \\& {\text{E}}\{ {\boldsymbol N}{{\boldsymbol N}^*}\} \otimes {\text{E}}\{ {({\boldsymbol N}{{\boldsymbol N}^*})^{\text{H}}}\} . \end{split} (16) 为简化公式形式, 令
{\boldsymbol{H}}({\boldsymbol{\psi}} ) = {\boldsymbol{KR}}({\boldsymbol{V}}({\boldsymbol{\psi}} )) ,{\boldsymbol{X}} 的四阶累积量{{\boldsymbol{C}}_{4X}} 表示为矩阵形式, 即{{\boldsymbol{C}}_{4X}} = ({\boldsymbol{H}} \otimes {{\boldsymbol{H}}^*}){{\boldsymbol{C}}_{4S}}{({\boldsymbol{H}} \otimes {{\boldsymbol{H}}^*})^{\text{H}}} + {{\boldsymbol{C}}_{4N}} . (17) 对阵列输出数据的四阶累积量矩阵
{{\boldsymbol{C}}_{4X}} 求协方差, 可表示为{\boldsymbol{R}}\_{{\boldsymbol{C}}_{4X}} = \frac{{{{\boldsymbol{C}}_{4X}}{{({{\boldsymbol{C}}_{4X}})}^*}}}{{MN \cdot MN}}. (18) 对
{\boldsymbol{R}}\_{{\boldsymbol{C}}_{4X}} 进行特征值分解, 分别得到信号子空间{{\boldsymbol{C}}_{\boldsymbol{S}}} \in {{\mathbb{C}}^{{{(NM)}^2} \times {I^2}}} 和噪声子空间{{\boldsymbol{C}}_N} \in {{\mathbb{C}}^{{{(NM)}^2} \times ({{(NM)}^2} - {I^2})}} 。最后, 根据MUSIC算法[1]定义空间谱公式, 可以得到由四阶累积量和Kroneker积变换的声压数据
{\boldsymbol{X}} 和阵列流形矢量{\boldsymbol{H(\psi )}} 定义的高阶矩阵变换方法—四阶累积量多重矩阵重构(FOC-MMR)法的归一化空间谱(NSS), 可表示为{\boldsymbol{P(\psi )}} = \frac{1}{{{{(MN)}^2}}}\frac{{{{({\boldsymbol{H}} \otimes {{\boldsymbol{H}}^*})}^{\text{H}}}({\boldsymbol{H}} \otimes {{\boldsymbol{H}}^*})}}{{[{{({\boldsymbol{H}} \otimes {{\boldsymbol{H}}^*})}^{\text{H}}}{{\boldsymbol{C}}_N}]{{[{{({\boldsymbol{H}} \otimes {{\boldsymbol{H}}^*})}^{\text{H}}}{{\boldsymbol{C}}_N}]}^{\text{H}}}}}. (19) 式(19)中, 空间谱
{\boldsymbol{P(\psi ) }}\in {{\mathbb{C}}^{{I^2} \times {I^2}}} 包含I 个声源的DOA信息, 将{\boldsymbol{P(\psi )}} 看作目标函数[23], 其中{\boldsymbol{\psi}} {\text{ = }} [{{\boldsymbol{\psi}} _1},\cdots, {{\boldsymbol{\psi}} _i},\cdots,{{\boldsymbol{\psi }}_I}{\text{]}} 是函数的自变量, 式(19)求解最大值{\boldsymbol{P(\psi )}} 的问题定义为式(20)。以分辨率1°对空间\theta \in [0^\circ , 180^\circ ] 和\varphi \in [180^\circ，360^\circ] 划分, 即可求得令{\boldsymbol{P(\psi )}} 最大的{\boldsymbol{\delta}} = (\varphi ,\theta ) , 该数值解即为DOA估计值,{\boldsymbol{\delta }} = (\varphi ,\theta ) = \arg \max ({\boldsymbol{P(\psi )}}). (20) 上述公式中,
\odot 和\otimes 分别表示矩阵的Khatri-Rao积和Kronecker积,{( \cdot )^*} 表示矩阵的复共轭,{( \cdot )^{\text{H}}} 表示矩阵的共轭转置。2. 仿真实验与结果分析
在平面矩形阵列中包含有两个或两个以上线性阵列, 线性阵列在几何结构上为矩形平面阵列的某行, 设置仿真阵列模型为均匀线性阵列(ULA)。将提出的四阶累积量多重矩阵重构(FOC-MMR)方法与频率平滑最大似然估计法(FS-MLE)应用于均匀线阵(ULA, 阵元
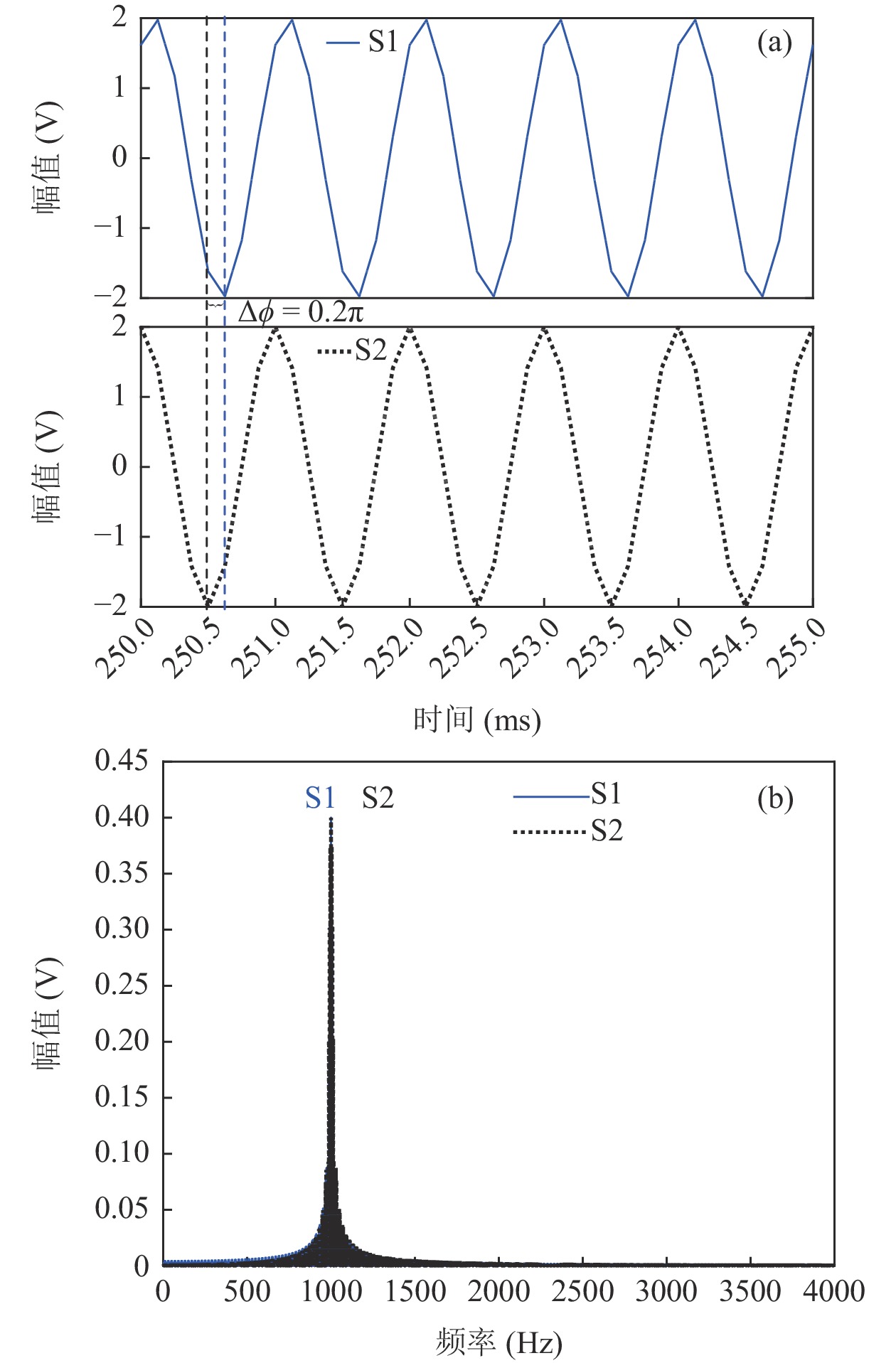
M = 4 , 有效孔径{K_a} = 4d ), 估计两个相干信号的方位。构建仿真信号源为一组相干系数为0.81的周期性单频矩形脉冲信号(频率f = 1 kHz, 相位差\Delta \phi = 0.2\pi , 幅值a = 2 , 占空比为20%), 脉冲周期为0.25 s, 信号总长度为1 s。构建的仿真信号时域波形和频谱如图2(a)和图2(b) 所示。为评估均方根误差, 对估计
I 个信号源的DOA时, 进行L 次独立实验的均方根误差(RMSE)给出定义:\begin{split}& \text { RMSE }=\\& \sqrt{\frac{1}{L} \sum_{l=1}^L \frac{\left(\theta_1^{(l)}-\theta_1^{\prime(l)}\right)^2 + \cdots + \left(\theta_i^{(l)}-\theta_i^{\prime(l)}\right)^2 + \cdots + \left(\theta_I^{(l)}-\theta_I^{\prime(l)}\right)^2}{L}}, \end{split} (21) 式中,
{\theta _i} 为信号与线阵法线的夹角,\theta {'_i} 为算法估计的信号DOA,I 为信号的个数,L 为独立试验的次数。2.1 实验1: 评估不同SNR时的DOA估计精度
为衡量两种算法在估计相干信号DOA时的精度, 按照信号和噪声的功率比值
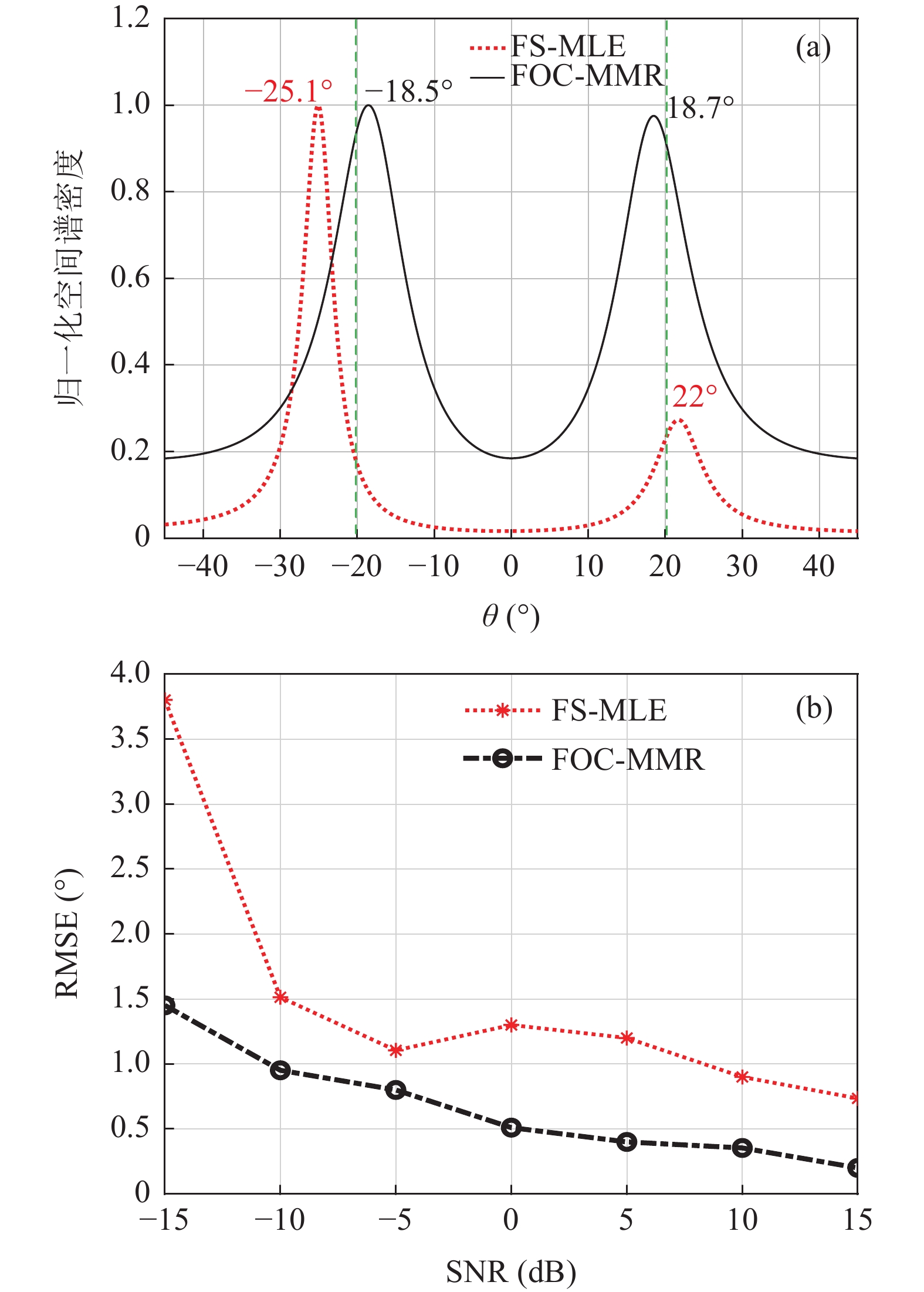
{\text{SNR}} = 10\lg ({P_S}/{P_N}) 在仿真信号中加入不同信噪比的高斯白噪声, 通过归一化空间谱和DOA估计结果的RMSE曲线来评估算法的估计精度。在仿真信号中添加信噪比为−15 dB的高斯白噪声, 采用基于ULA (M = 4)的FS-MLE和FOC-MMR算法进行DOA估计。当声源角度为θ1 = −20°和θ2 = 20°时, 获得的归一化空间谱如图3(a)所示。可见, 当信噪比低至−15 dB时, FS-MLE算法估计相干信号源的精度较低, 且对幅值相等的两个信号的归一化空间谱峰值估计差距较大; 而FOC-MMR方法的估计精度高于FS-MLE算法, 且两个相干信号的归一化空间谱峰值差异较小, 可以有效地辨识仅相位和波达角度不同的两个相干信号。
![]()
图 3 实验1 (a) 归一化空间谱(ULA(M = 4), SNR= −15 dB，θ1 = −20°, θ2 = 20°); (b) FS-MLE和FOC-MMR在不同SNR下的DOA估计值的RMSE曲线(θ1 = −20°, θ2 = 20°)为进一步评估算法在不同信噪比下的DOA估计精度, 构建信噪比从−15 dB增加至15 dB, 步长为5 dB, 采用上述两种方法对信号源进行DOA估计。每个信噪比进行L=100次独立试验, 然后根据式(21)评估算法的估计精度, 结果如图3(b)所示。可见, 基于ULA的FS-MLE方法在SNR < −10 dB时估计相干信号DOA的误差较大(>3.5°); 而FOC-MMR方法的DOA估计精度RMSE在不同信噪比下均能保持在1.5°以内, 当SNR>5 dB时, RMSE值控制在0.5°以内。该仿真实验证明FOC-MMR方法能够有效抑制高斯白噪声的干扰, 并且能够实现高阶信号和噪声特征向量之间能量的有效分离, 且对相干信号的幅值在归一化空间谱中有较准确的估计。
2.2 实验2: 评估不同方位间隔Δθ的分辨性能
对于单次DOA估计仿真实验, 两个相干信号的DOA估计值分别为
\theta {'_1} 和\theta {'_2} , 正确分辨DOA的定义[27]:\left| {{\theta _1} - \theta {'_1}} \right| + \left| {{\theta _2} - \theta {'_2}} \right| < \left| {{\theta _1} - {\theta _2}} \right|. (22) 当
\begin{split} {\text{RMSE}} =& \sqrt {({{\left| {{\theta _1} - \theta {'_1}} \right|}^2} + {{\left| {{\theta _2} - \theta {'_2}} \right|}^2})/2} < \\& \sqrt {{{\left| {{\theta _1} - {\theta _2}} \right|}^2}/2 - \left| {{\theta _1} - \theta {'_1}} \right| \cdot \left| {{\theta _2} - \theta {'_2}} \right|} < \left| {{\theta _1} - {\theta _2}} \right| \end{split} 时, 即认为两个仿真信号的方位可以被正确估计。
分别利用基于ULA (
M = 4 )的FS-MLE法和FOC-MMR法对上述相干信号源进行DOA估计。为使仿真信号更贴近真实信号, 在仿真信号中添加了SNR=10 dB的高斯白噪声。当两相干信号的方位分别为θ1 = −20°和θ2 = −10°时, 即方位间隔\Delta \theta = 10^\circ , 其DOA估计结果的归一化空间谱如图4(a)所示。可见, 当相干信号的临近角度差\Delta \theta = 10^\circ 时, 与FS-MLE算法相比, FOC-MMR算法的空间分辨能力和DOA估计精度更高, 且主瓣宽度更窄。![]()
图 4 实验2 (a) 方位间隔\Delta \theta = 10^\circ 的归一化空间谱(SNR = 10 dB, θ1 = −20°, θ2 = −10°); (b) FS-MLE和FOC-MMR在不同\Delta \theta 下的DOA估计值的RMSE曲线(θ1固定, θ2从−15°变化至10°)为评估两种方法分辨相干信号的方位间隔
\Delta \theta 的能力, 保持仿真信号S1的方位θ1 = − 20°不变, 仿真信号S2的方位θ2从 −15°变化至10°, 步长为1°, 即信号的方位间隔\Delta \theta 从5°变化至30°。采用上述两种方法分别对声源进行DOA估计, 并进行了L = 100次独立试验。根据式(21)和式(22)评估算法的估计精度和正确分辨信号能力, 结果如图4(b)所示。可见, 当\Delta \theta 低至5°时, 两种算法都可以正确分辨相干信号的DOA, 但是FOC-MMR方法的测向估计性能高于FS-MLE算法, 且随着\Delta \theta 的增加, FOC-MMR正确分辨信号的能力始终高于FS-MLE算法。2.3 实验3: 评估不同数据帧长、占空比和周期数据长度的算法性能
为了衡量FOC-MMR算法的运算复杂度, 在上述仿真信号中加入SNR = −15 dB的高斯白噪声, 变换数据帧长由512点增加至2048点, 步长为512点。评估时采用同一运行环境, 电脑配置为Intel (R) Core (TM) i7-7500U CPU @ 2.70 GHz, 8 GB RAM。评估两算法估计DOA的运行时间和RMSE值, 结果如表1所示, 随着数据帧长增加, 两种算法运行时间均呈增大趋势, 而FOC-MMR法的趋势更加明显。对于DOA估计的精度, FOC-MMR法的RMSE值在不同数据帧长下均优于FS-MLE法。综合运算时间和估计精度考虑, 得到FOC-MMR法的最佳数据帧长为1024。
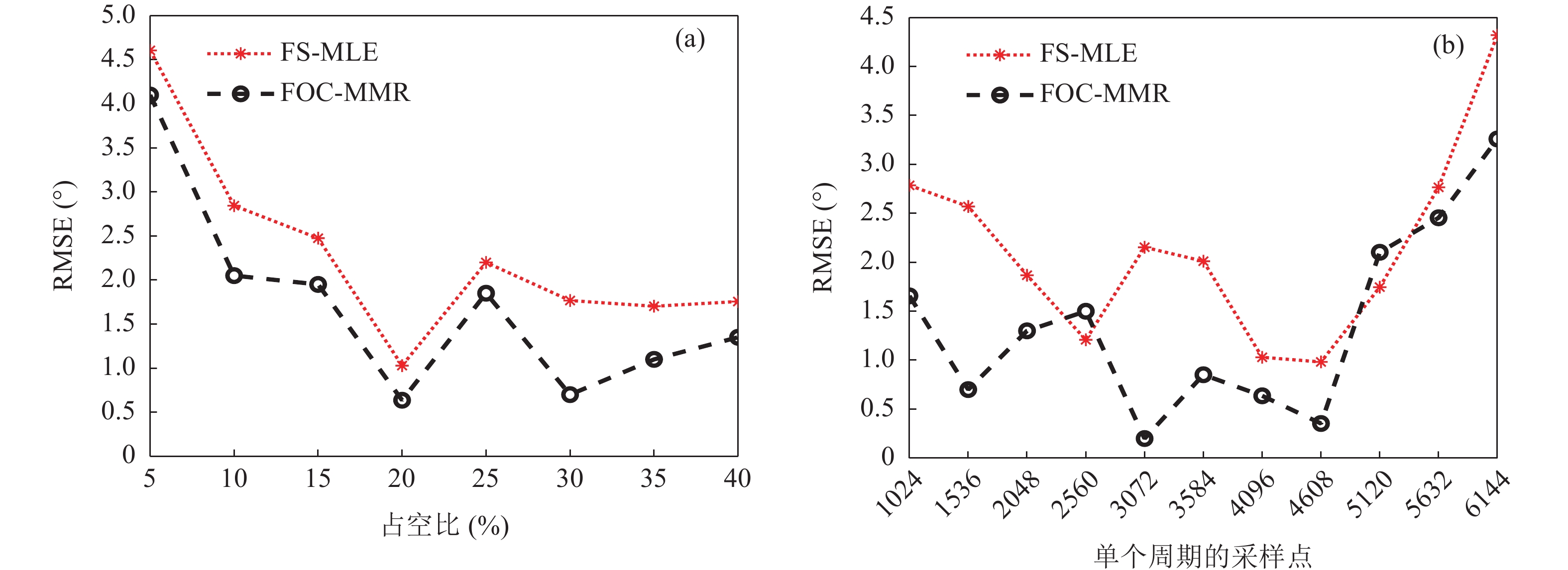
表 1 不同数据帧长下各算法的运行时间和RMSE值(100次运行平均)帧长 512 1024 1536 2048 算法 FS-MLE FOC-MMR FS-MLE FOC-MMR FS-MLE FOC-MMR FS-MLE FOC-MMR 时间 (s) 0.75 2.19 2.68 8.09 5.32 19.75 7.12 37.24 RMSE (°) 4.2 3.84 2.75 1.92 2.15 1.35 3.15 2.29 上述数据帧长是在仿真信号占空比为20%下确定的, 当矩阵重构的数据帧长固定为1024采样点, 变换脉冲信号的占空比(5%~40%), 采用两种方法分别对声源进行DOA估计, 重复进行L = 100次独立试验, 其DOA估计精度随信号占空比的变化如图5(a)所示。可见, 随着脉冲信号占空比下降, 两种算法的DOA估计精度呈下降趋势, 原因是参与频谱变换的一帧数据(1024个采样点)包含过多的无用背景噪声数据(尤其当占空比小于10%时), 导致经奇异值分解得到的信号特征向量包含的信号能量较低, 因而无法实现仿真信号方位的有效估计; 随着占空比的增加, 参与矩阵重构的信号长度包含了较多的信号特征, 从而方位估计精度得到了提高。可见, 若脉冲声源信号的占空比较低, 应适当降低参与频谱变换的采样点数。
![]()
图 5 实验3 (a) 每周期采样点固定, 不同占空比下的各算法的RMSE曲线(θ1 = −20°, θ2 = 20°, 每个周期4096采样点); (b) 占空比一定, 调节每周期采样点长度的各算法的RMSE曲线(θ1 = −20°, θ2 = 20°, 占空比20%)固定信号占空比为20%, 改变脉冲信号周期长度(即每周期采样点数), 评估两种算法的估计精度, 得到的RMSE曲线如图5(b)所示。当每周期采样点数小于4608时, FOC-MMR算法的RMSE值均能保持在2°以内; 随着每周期采样点数的增加, 进行频谱变换的一帧声压数据包含更多的信号特征, 所以两种算法的DOA估计精度都逐渐提高。当采样点数大于5120, 即脉宽大于1024个采样点时, 由于参与频谱变换的第二帧数据的信号长度较短, 因而两种算法的DOA估计精度显著下降。可见, 当占空比为20%时, 随着周期信号采样点数的增加, 应适当调整参与频谱变换的采样点数。
从上述仿真实验的归一化空间谱(NSS)图和RMSE曲线可以发现, 当FOC-MMR方法应用在均匀线阵(ULA, M = 4)时, 由于四阶累积量重构后的频域声压数据矩阵可以有效抑制高斯噪声, 使得该方法在SNR低至−15 dB时依然具有较高的空间分辨率及DOA估计精度。受线性阵列孔径的限制, 随着待测信号的临近角度
\Delta \theta 减小, 导致信号特征向量和噪声特征向量造成较大的混叠, 当SNR≤10 dB时, 算法不能有效区分\Delta \theta < 5^\circ 的相干信号。当脉冲信号的占空比降低时, 算法的估计精度呈下降趋势, 这是由于参与频谱变换的信号长度较短, 导致包含的信号特征较少。因此, 当占空比较低或周期信号采样点数较多时, 应适当调整参与频谱变换的数据帧长。3. 基于面阵的多脉冲声源定位实验
为验证提出的方法(FOC-MMR)在估计相干脉冲声源DOA的有效性和准确性, 采用阵元间距d = 0.16 m的8通道均匀矩形传声器阵列(URA), 估计相干脉冲声源(频率f = 1 kHz, 幅值
a = 1 , 相位差\Delta \phi = 0.2\pi , 相干系数为0.76)的DOA, 脉冲信号时域波形图和相位差如图6(a)和图6(b)所示。如图6(d)所示, 以距地面高h = 1.2 m的阵列中心为原点建立坐标系, 相干脉冲声源S1和S2均位于阵列正前方1.0 m处, 即y = −1.0 m平面。实验中, 采样率Fs = 8 kHz, 传声器型号为CHZ-213+YG-201, 为了评估算法的鲁棒性和估计精度, 每组实验统计10次DOA估计结果; 为评估算法对高斯噪声的抑制作用, 在阵列获取的声压数据中分别加入了SNR = 5 dB和SNR = 10 dB的高斯白噪声。为衡量DOA估计精度, 通过均方根误差均值e来实现, 其定义如下:e = \frac{1}{n}\sqrt {\frac{{{{({\varphi _1} - \varphi {'_1})}^2} + {{({\theta _1} - \theta {'_1})}^2} + {{({\varphi _2} - \varphi {'_2})}^2} + {{({\theta _2} - \theta {'_2})}^2}}}{4}} , (23) 式中, n表示每组实验测量的次数,
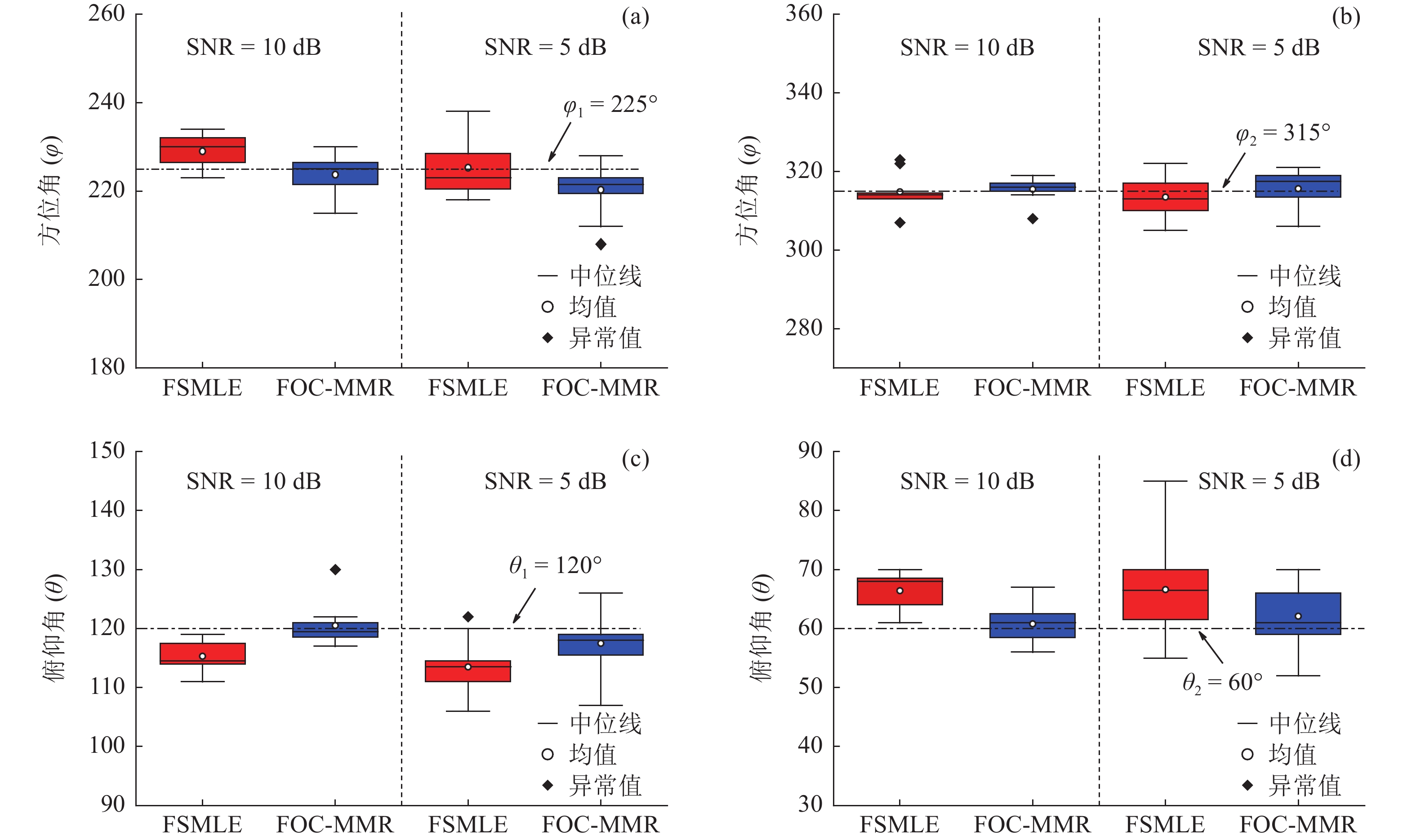
{{\boldsymbol{\delta}} _1} = ({\varphi _1},{\theta _1}) ,{{\boldsymbol{\delta}} _2} = ({\varphi _2},{\theta _2}) 和{\boldsymbol{\delta}} {'_1} = (\varphi {'_1},\theta {'_1}) ,{\boldsymbol{\delta}} {'_2} = (\varphi {'_2},\theta {'_2}) , 分别为声源DOA的实际值与估计值。在此将声源放置在4个不同的位置, 共进行了两组实验, 并且对阵列获取的数据添加了不同信噪比(SNR = 5 dB,10 dB)的高斯白噪声。利用文献[9]的频率平滑最大似然估计法(FS-MLE)和FOC-MMR方法进行DOA估计, 以空间分辨率1°对
\theta \in [0^\circ ,180^\circ ] 和\varphi \in [180^\circ, 360^\circ] 空间区域进行谱估计, 并根据声场成像结果和均方根误差均值e对比算法的空间分辨率、鲁棒性和测向精度。下述声场成像图中, 黑色 “o”和数字表示声源实际DOA, 红色“* ”和数字表示声源估计DOA。两相干声源实际DOA为
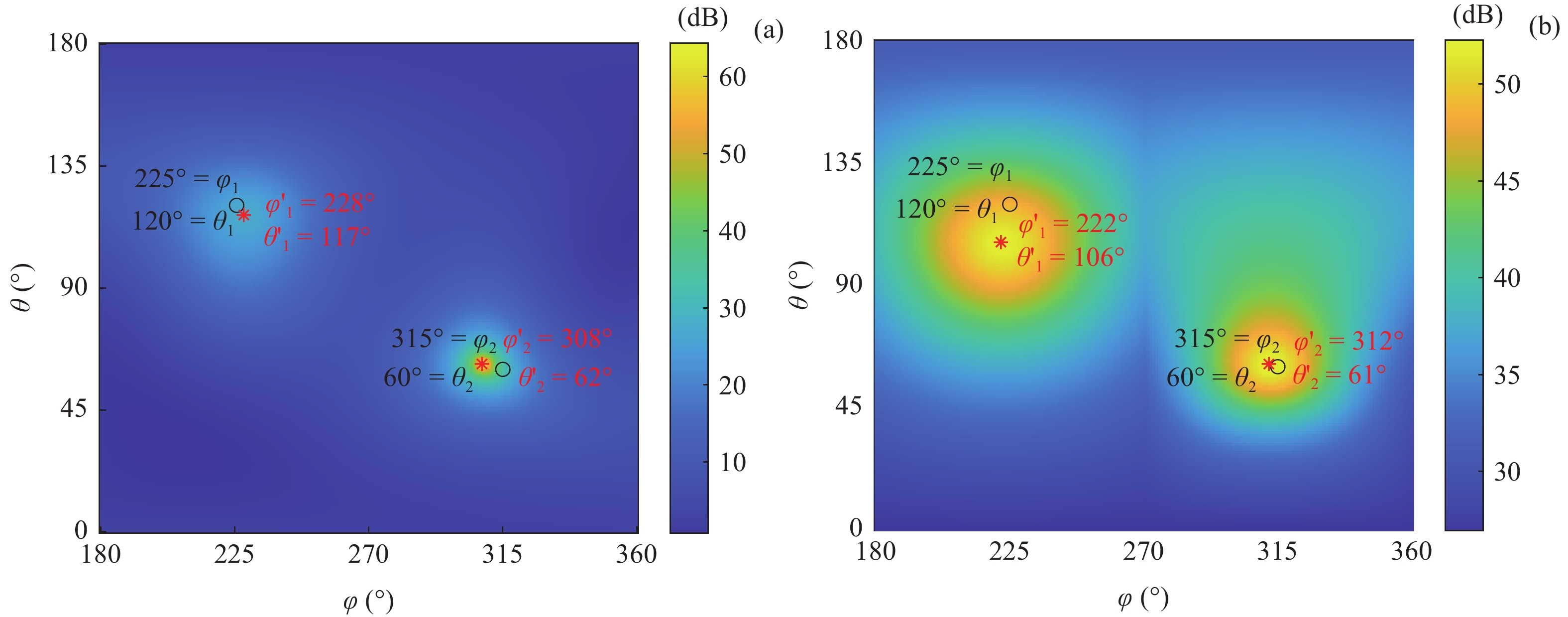
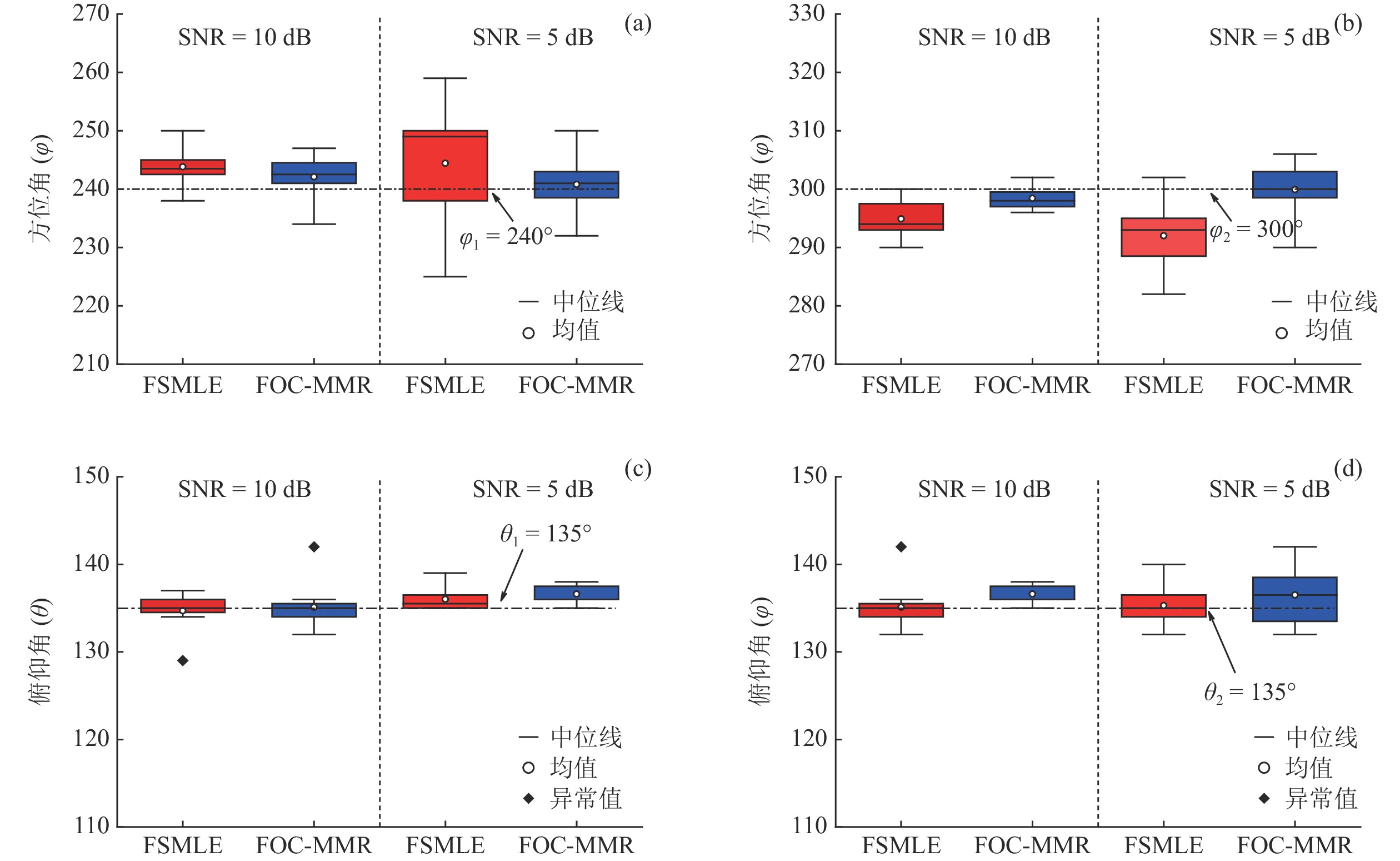
[{{\boldsymbol{\delta}} _1},{{\boldsymbol{\delta}} _2}] = [(225^\circ ,120^\circ ), (315^\circ ,60^\circ )] , DOA估计值的10次统计结果如图7所示, e1和e2分别表示由式(23)计算的FS-MLE和FOC-MMR方法的均方根误差均值e。可以发现随着信噪比的降低, FS-MLE算法抑制高斯白噪声的能力逐渐降低, 根据图7(c)和图7(d)可以发现, 当两相干声源的俯仰角\theta 的角度差较大时, 该算法的估计精度会显著下降; 由于四阶累积量的矩阵重构致使FOC-MMR算法可以有效抑制高斯白噪声, 其DOA估计值的中位数更接近实际值, 且DOA估计值和异常值较相同情况下的FS-MLE算法更集中、更小, 证明提出的方法在信噪比低至SNR = 5 dB时依旧具有较高的鲁棒性和测向估计精度, 根据算法对声场重建如图8所示。![]()
图 7 DOA估计值的10次统计结果 (a){{\boldsymbol{\delta}} _1} 的方位角{\varphi _1} ; (b){{\boldsymbol{\delta}} _2} 的方位角{\varphi _2} ; (c){{\boldsymbol{\delta}} _1} 的俯仰角{\theta _1} ; (d){{\boldsymbol{\delta}} _2} 的俯仰角{\theta _2} (实验1: SNR = 5 dB时e1 = 7.53°和e2 = 5.54°, SNR = 10 dB时e1 = 5.68°和e2 = 3.31°)为进一步验证算法的定位精度, 设置两相干声源实际DOA为
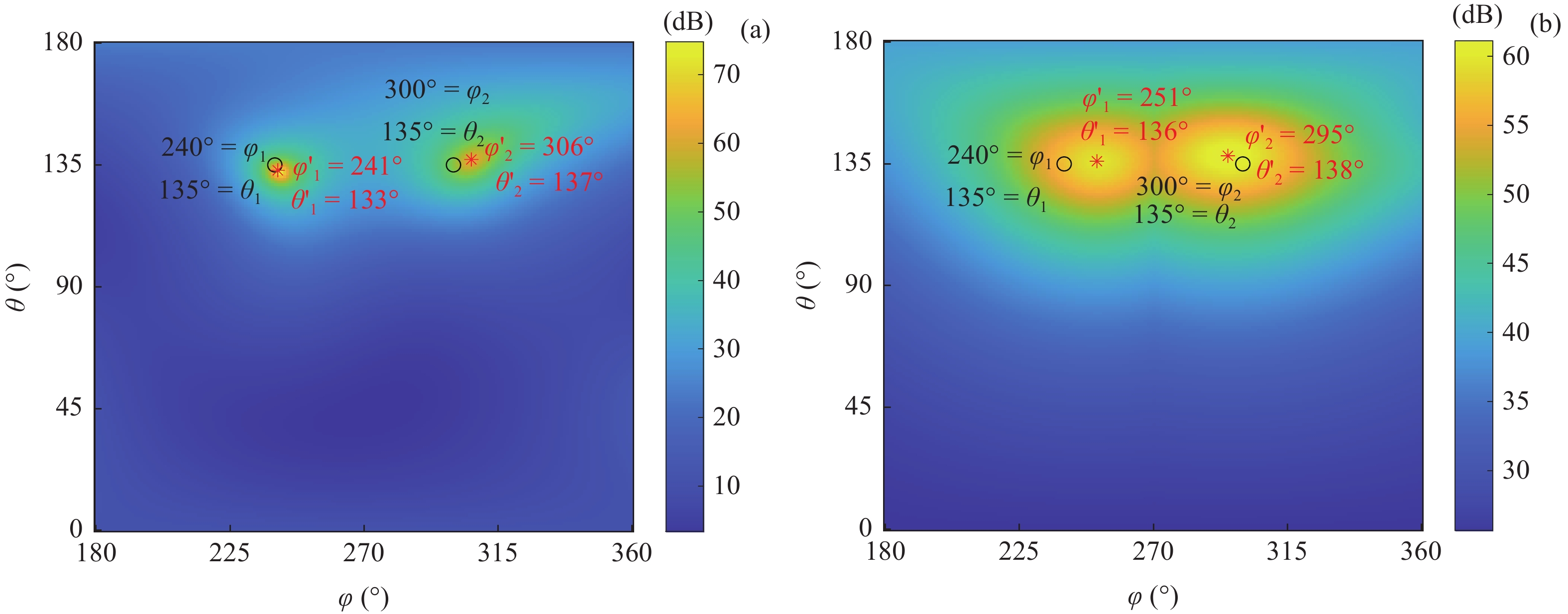
[{{\boldsymbol{\delta}} _1},{{\boldsymbol{\delta}} _2}] = [(240^\circ ,135^\circ ),(300^\circ ,135^\circ )] , 不同信噪比下DOA估计值的10次统计结果如图9所示。可见, 当方位角\Delta \varphi = 60^\circ 时, FS-MLE算法对方位角\varphi 多次估计结果的波动范围较大, 且\varphi ' 的中位数与真值\varphi 相差较大; FOC-MMR方法对方位角\varphi 的多次估计结果更加集中, 且\varphi ' 的中位数与真值\varphi 更接近, 如图9(a)和图9(b)所示。随着信噪比的降低, 两种算法的DOA估计结果波动程度增加, 且出现的异常估计值偏离实际值的程度更大, 而FOC-MMR法的DOA估计结果仍然集中在真值两侧, 证明该方法的空间分辨率要高于FS-MLE方法, 根据算法对声场重建如图10所示。![]()
图 9 DOA估计值的10次统计结果 (a){{\boldsymbol{\delta}} _1} 的方位角{\varphi _1} ; (b){{\boldsymbol{\delta}} _2} 的方位角{\varphi _2} ; (c){{\boldsymbol{\delta}} _1} 的俯仰角{\theta _1} ; (d){{\boldsymbol{\delta}} _2} 的俯仰角{\theta _2} (实验2: SNR=5 dB时e1=7.49°和e2=4.29°, SNR=10 dB时e1=4.23°和e2=2.68°)根据仿真实验可知当数据帧长为1024时, FOC-MMR方法的计算复杂度较低且测向精度更高, 所以相干脉冲声源DOA估计实验中FOC-MMR算法根据脉冲声信号的时域稀疏特性以1024采样点为窗宽进行STFT。通过对频域下的每窗声压数据进行四阶累积量重构以扩展虚拟阵元数据得到高阶协方差矩阵, 对包含全部相干信号特征的高阶满秩协方差矩阵进行SVD, 实现相干脉冲声源的高阶信号特征向量和高阶噪声特征向量(HO-NFV)的有效分离。不仅抑制了空气中低信噪比声信号混入的高斯白噪声, 还实现了相干脉冲声源DOA的有效估计。由信号频率和阵列结构确定与HO-NFV成正交匹配关系的高阶阵列流形矢量(HO-AMV), 利用式(19)和式(20)求解
{\boldsymbol{\psi}} {\text{ = [}}{{\boldsymbol{\psi}} _1},\cdots,{{\boldsymbol{\psi}} _i},\cdots,{{\boldsymbol{\psi}} _I}{\text{]}} 令空间谱函数{\boldsymbol{P(\psi )}} 取最大值, 即得到{\boldsymbol{\delta}} = (\varphi ,\theta ) 的估计值。以分辨率
1^\circ 对声源所处空间网格\theta \in [0^\circ ,180^\circ ] 和\varphi \in [180^\circ, 360^\circ] 进行划分, 经由算法只能有效估计位于网格点上的声源DOA, 若声源的实际DOA并未处在空间网格节点上(即离网格点), 则需要以更小的分辨率划分空间网格, 由此带来的计算量将大大增加。经过实验验证, 在相同运算环境下, FS-MLE[9]方法的运算速度约为FOC-MMR方法的2.5倍。(本节的计算结果均保留两位小数。)
4. 结论
依据传声器阵列信号的时频域稀疏特性, 提出对阵列信号施以四阶累积量重构扩展阵元结构信息以实现相干声源信号的协方差矩阵秩的补充, 通过高阶奇异值分解获得正交匹配的HO-NFV和高阶信号特征向量, 原始AMV及其复共轭的克罗内克积包含了扩展阵元的结构信息, 且根据NFV与AMV的正交性, 经理论验证扩展后的HO-NFV与HO-AMV也同样存在正交匹配性, 通过FOC-MMR算法达到估计相干信号的DOA的目的。FOC-MMR方法的优点在于通过高阶累积量的阵列扩展性和噪声抑制能力, 在SNR低至−15 dB时依旧具有较高的相干信号DOA估计能力。当采用基于ULA (M = 4)和URA(M = 8)估计频率相同但相位不同的相干信号的DOA时, 经仿真和实验估计结果分析, 可得出如下结论: (1) 当SNR = 10 dB时, 经过四阶累积量重构的频域阵列声压数据可以补充欠正定协方差矩阵的秩, 可正确分辨的两相干信号方位间隔
\Delta \theta 可以低至5°; (2) 综合考虑数据帧长和占空比对算法性能的影响, 进行矩阵重构的数据帧长为1024采样点时, 脉冲信号的占空比应大于5%; 当信号占空比较低(每周期采样点数一定)或每周期采样点数较多(占空比一定)时, 应适当调整参与频谱变换的数据帧长, 以确保每帧数据包含较长的信号; (3) 统计相同条件下多次DOA估计值, 相较于FS-MLE算法, FOC-MMR算法的DOA估计值更加集中, 估计精度更高, 且受噪声影响较小。 -
![]()
图 3 实验1 (a) 归一化空间谱(ULA(M = 4), SNR= −15 dB，θ1 = −20°, θ2 = 20°); (b) FS-MLE和FOC-MMR在不同SNR下的DOA估计值的RMSE曲线(θ1 = −20°, θ2 = 20°)
![]()
图 4 实验2 (a) 方位间隔
\Delta \theta = 10^\circ 的归一化空间谱(SNR = 10 dB, θ1 = −20°, θ2 = −10°); (b) FS-MLE和FOC-MMR在不同\Delta \theta 下的DOA估计值的RMSE曲线(θ1固定, θ2从−15°变化至10°)![]()
图 5 实验3 (a) 每周期采样点固定, 不同占空比下的各算法的RMSE曲线(θ1 = −20°, θ2 = 20°, 每个周期4096采样点); (b) 占空比一定, 调节每周期采样点长度的各算法的RMSE曲线(θ1 = −20°, θ2 = 20°, 占空比20%)
![]()
图 7 DOA估计值的10次统计结果 (a)
{{\boldsymbol{\delta}} _1} 的方位角{\varphi _1} ; (b){{\boldsymbol{\delta}} _2} 的方位角{\varphi _2} ; (c){{\boldsymbol{\delta}} _1} 的俯仰角{\theta _1} ; (d){{\boldsymbol{\delta}} _2} 的俯仰角{\theta _2} (实验1: SNR = 5 dB时e1 = 7.53°和e2 = 5.54°, SNR = 10 dB时e1 = 5.68°和e2 = 3.31°)![]()
图 9 DOA估计值的10次统计结果 (a)
{{\boldsymbol{\delta}} _1} 的方位角{\varphi _1} ; (b){{\boldsymbol{\delta}} _2} 的方位角{\varphi _2} ; (c){{\boldsymbol{\delta}} _1} 的俯仰角{\theta _1} ; (d){{\boldsymbol{\delta}} _2} 的俯仰角{\theta _2} (实验2: SNR=5 dB时e1=7.49°和e2=4.29°, SNR=10 dB时e1=4.23°和e2=2.68°)表 1 不同数据帧长下各算法的运行时间和RMSE值(100次运行平均)
帧长 512 1024 1536 2048 算法 FS-MLE FOC-MMR FS-MLE FOC-MMR FS-MLE FOC-MMR FS-MLE FOC-MMR 时间 (s) 0.75 2.19 2.68 8.09 5.32 19.75 7.12 37.24 RMSE (°) 4.2 3.84 2.75 1.92 2.15 1.35 3.15 2.29 
下载: 导出CSV
-
[1] Schmidt R O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag, 1986; 34(3): 276—280 DOI: 10.1109/TAP.1986.1143830
[2] Richard R, Thomas K A. Esprit-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process., 1989; 37(7): 984—995 DOI: 10.1109/29.32276
[3] 胡盈绮, 邓科, 殷勤业. 采用前向空间平滑分组的混合信号波达方向估计算法. 西安交通大学学报, 2020; 54(9): 164—172 DOI: 10.7652/xjtuxb202009019 [4] Wen J, Liao B, Guo C. Spatial smoothing based methods for direction-of-arrival estimation of coherent signals in nonuniform noise. Digital Signal Process., 2017; 67: 116—122 DOI: 10.1016/j.dsp.2017.05.002
[5] Pan J, Sun M, Wang Y, et al. An enhanced spatial smoothing technique with ESPRIT algorithm for direction of arrival estimation in coherent scenarios. IEEE Trans. Signal Process., 2020; 68: 3635—3643 DOI: 10.1109/TSP.2020.2994514
[6] Arun P S, Nachiketa T. An improved method to localize simultaneously close and coherent sources based on symmetric-Toeplitz covariance matrix. Appl. Acoust., 2021; 182: 108176 DOI: 10.1016/j.apacoust.2021.108176
[7] 张石, 许方晗, 佘黎煌, 等. 基于重构噪声子空间的相干信号DOA估计. 东北大学学报(自然科学版), 2021; 42(12): 1696—1700 DOI: 10.12068/j.issn.1005-3026.2021.12.004 [8] 时胜国, 李赢. 声矢量圆阵宽带相干目标MVDR方位估计. 应用声学, 2019; 38(4): 530—539 DOI: 10.11684/j.issn.1000-310X.2019.04.009 [9] Hu Y, Lu J, Qiu X. Direction of arrival estimation of multiple acoustic sources using a maximum likelihood method in the spherical harmonic domain. Appl. Acoust., 2018; 135: 85—89 DOI: 10.1016/j.apacoust.2018.02.005
[10] 陈璐, 毕大平, 崔瑞, 等. 嵌套阵列最大似然估计测向算法. 航空学报, 2017; 38(11): 265—276 DOI: 10.7527/S1000-6893.2017.321212 [11] Hu Y, Lu J, Qiu X. A maximum likelihood direction of arrival estimation method for open-sphere microphone arrays in the spherical harmonic domain. J. Acoust. Soc. Am, 2015; 138(2): 791—794 DOI: 10.1121/1.4926907
[12] 李秀坤, 李婷婷, 谷新禹. 典型概率密度背景下四阶累积量波束形成的阵增益. 声学学报, 2014; 39(5): 557—564 DOI: 10.15949/j.cnki.0371-0025.2014.05.010 [13] 单泽彪, 鲁胜麟, 刘小松, 等. 基于高阶累积量的阵列式超声波传感器风速风向测量. 仪器仪表学报, 2021; 42(6): 279—286 DOI: 10.19650/j.cnki.cjsi.J2107773 [14] 张君, 陈志菲, 常继红, 等. 声矢量锥形阵的高阶累积量波达方向估计. 声学学报, 2019; 44(6): 970—985 DOI: 10.15949/j.cnki.0371-0025.2019.06.003 [15] Liu J, Zhou W, Wang X. Fourth-order cumulants-based sparse representation approach for DOA estimation in MIMO radar with unknown mutual coupling. Signal Process., 2016; 128: 123—130 DOI: 10.1016/j.sigpro.2016.03.019
[16] 齐子森, 郭英, 王布宏, 等. 基于四阶累积量的共形阵列波达方向估计算法. 电波科学学报, 2011; 26(4): 735—744 DOI: 10.13443/j.cjors.2011.04.025 [17] Yılmaz Ö, Rickard S. Blind separation of speech mixtures via time-frequency masking. IEEE Trans. Signal Process., 2004; 52(7): 1830—1847 DOI: 10.1109/TSP.2004.828896
[18] Ye Z F, Dai J S. DOA estimation for nonuniform circular array with mutual coupling based on fourth order cumulants. J. Univ. Sci. Technol. China, 2008; 38(7): 770—775
[19] 胡定玉, 刘馨悦, 李曷冰, 等. 采用稀疏测量的高分辨率相干声场分离. 声学学报, 2020; 45(4): 563—570 DOI: 10.15949/j.cnki.0371-0025.2020.04.013 [20] 徐亮, 胡鹏, 张永斌, 等. 可用于相干声源的快速反卷积声源成像算法. 机械工程学报, 2018; 54(23): 82—92 DOI: 10.3901/JME.2018.23.082 [21] 王心怡, 罗松. 双目标相干源窄带信号波达方向估计算法. 声学技术, 2014; 33(4): 363—366 DOI: 10.3969/j.issn1000-3630.2014.04.016 [22] Perotin L, Vincent E. CRNN-based multiple DoA estimation using acoustic intensity features for ambisonics recordings. IEEE J. Sel. Top. Signal Process., 2019; 13(1): 22—33 DOI: 10.1109/JSTSP.2019.2900164
[23] Hu Y, Abhayapala T D, Samarasinghe P N. Multiple source direction of arrival estimations using relative sound pressure based MUSIC. IEEE-ACM T AUDIO SPE, 2021; 29: 253—264
[24] Van Trees H L. 最优阵列处理技术. 汤俊, 等 译. 北京: 清华大学出版社, 2008: 75—208 [25] Fontgalland G, Pedro H J G. Normality and correlation coefficient in estimation of insulators’ spectral signature. IEEE Signal Process. Lett., 2015; 22(8): 1175—1179 DOI: 10.1109/LSP.2015.2390638
[26] Sidki M, Nicolas J. Localization of coherent and incoherent sound sources via an optimization process. J. Acoust. Soc. Am, 1988; 84(2): 639—644 DOI: 10.1121/1.396842
[27] Gershman A B. Direction finding using beamspace root estimator banks. IEEE Trans. Signal Process., 1998; 46(11): 3131—3135 DOI: 10.1109/78.726831
-
期刊类型引用(3)
1. 潘博志，何宏昌，范冬林，宫子怡，刘镇豪. 利用改进MUSIC方法进行洋流方位估计. 测绘通报. 2024(06): 134-138 . 
百度学术
2. 梁国龙 ，滕远鑫 ，王晋晋 ，付进 . 一种适用于半互质阵的高精度波达方向估计方法. 电子与信息学报. 2024(08): 3228-3237 . 百度学术
3. 田野，陈海艳，赵敏，方军，徐刚，孙守宇，王晓航. 基于互谱矩阵估计的泄漏源超声阵列定位技术研究. 压力容器. 2023(12): 71-79 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 339
- HTML全文浏览量: 19
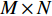
- PDF下载量: 65
- 被引次数: 7
